战术导弹的离散突风响应鲁棒控制研究

赵长见 王洪波 廖选平 王 亮

1. 国防科技大学航天科学与工程学院，长沙410073 2. 中国运载火箭技术研究院，北京100076



战术导弹的离散突风响应鲁棒控制研究

赵长见1,2王洪波1,2廖选平1,2王 亮2

1. 国防科技大学航天科学与工程学院，长沙410073 2. 中国运载火箭技术研究院，北京100076

研究了战术导弹在穿越离散突风区域时弹体的动力学响应鲁棒控制，给出了导弹在穿越突风区时的运动方程、导弹结构动力学模型、“1-cos”突风模型和控制模型，其中不仅考虑了弹体在突风区的刚体运动，而且考虑了弹体位置及空气舵位置的结构动力学响应引起的附加攻角，突风对空气舵的滞后影响效果，以及空气舵控制舵偏引起的控制力等。通过算例研究了导弹在穿越突风过程中使用空气舵对弹体的结构动力学响应进行控制，及弹体H∞控制方法，设计了最优控制器。研究发现，施加控制后的弹体结构动力学响应明显衰减。 关键词 振动；模态；离散突风； H∞控制；导弹

战术导弹飞行时会遭受大气干扰，该干扰可分为大尺度和短尺度扰动。其中，前者是因为地球自转引起的高空大气环流，比较有规律；后者是因为局部气流瞬态变化产生，通常称为突风。分析时一般有统计方法和时域表述2种方法。统计方法是将风速表示为风速波形和频率随时间连续变化的功率谱密度，时域表述方法是将风速表示为风速随空间和时间分布的时域函数。显然，无论是大尺度和短尺度大气扰动，都会影响导弹的结构安全、电气设备的可靠性及飞行控制精度。在战术导弹设计时，针对大尺度扰动，一般使用平均风修正及制导控制设计等方法来克服其影响。而针对短尺度扰动，它是偶然事件，无规律性，导弹对其适应性完全靠控制系统的控制能力，因此对于导弹在穿越突风区域的姿态控制研究很有必要。

国内外学者专家在研究突风对飞行器影响方面做了较多的研究。王冬[1]对较为细长的飞行器利用准定常气动力理论计算阵风响应载荷。徐焱[2]对飞机的离散突风响应作了分析。通过计算和分析，初步掌握了飞机遭遇离散突风时进行机翼气弹突风响应的理论基础及分析方法。张家齐[3]通过求解非定常的N-S方程，对NACA0012翼型的扑翼运动进行数值仿真，研究了阵风频率、幅值和扑翼运动参数对响应的影响。吴志刚和杨超[4]研究了导弹气动伺服弹性系统的连续与离散阵风响应的分析方法。杨秋艳和王育林[5]研究了连续阵风载荷计算的方法及其应用，通过在频域内联立求解结构振动方程，获得响应的频响函数。

对于振动响应的控制，学者们也做了较多研究。李山虎等[6]对伸展悬臂梁的独立模态振动控制进行了理论近似解的推导，在求解过程中使用了多尺度方法。Yang等[7]研究了在不同运动速度下运动梁的振动主动控制，由Hamilton原理得到梁和控制器的动力学模型，最后使用Lyapunov方法设计了边界控制法则。Liu和Huang[8]对轴向运动的悬臂梁横向振动控制进行了研究。吴志刚和陈磊等[9]在时域连续和离散阵风响应方程的基础上，设计3种不同的阵风减缓控制方案并进行对比分析。曹九发[10]研究了飞机阵风响应仿真计算方法及载荷减缓技术，采用LQG/LIT控制方法开展了控制律设计。

一方面，现阶段在计算突风对战术导弹的影响时，仅考虑了连续突风对导弹的影响，而未考虑离散突风的影响，导弹穿越离散突风时结构动力学响应及动载荷可能更恶劣；另一方面，战术导弹对突风影响的鲁棒控制是个值得探讨的领域。因此，本文在研究导弹穿越离散突风时的结构动力学响应时，使用鲁棒控制理论对弹体响应进行控制。

1 穿越突风区的导弹运动方程

定义坐标系：坐标原点为质心，沿弹轴为x向，指向前为正；y轴在俯仰平面垂直于x轴向上为正，采用右手坐标系得到z轴。

假设导弹前方存在一个与飞行速度垂直的突风区，导弹此时是配平状态。考虑如图1的导弹，弹长为l，飞行速度为V，由于受到阵风速度wg(t)、导弹沉浮运动Z(向下为正)、导弹俯仰运动θ(抬头为正)和导弹的弹性振动y(x,t)的影响，在导弹压心和空气舵分别产生附加攻角Δαw和ΔαT，分别生成附加升力ΔLw和ΔLT，导弹进行弹体响应控制的附加舵偏角为Δαc，可产生附加控制力ΔLC。

图1 进入突风区后考虑各种增量的导弹

一方面在计算附加攻角Δαw和ΔαT时，考虑导弹相对突风在垂向的运动和导弹俯仰姿态的改变，另一方面在计算空气舵附加攻角时，需考虑突风影响的滞后。计算公式分别如下：

(1)

(2)

式中，Zc为质心处沉浮位移，lw和lT分别为压心和空气舵距质心的距离。

弹身和空气舵处的附加升力ΔLw和ΔLT计算公式如下：

ΔLw=qsCαΔαw

(3)

考虑弹体结构动力学一阶弹性方程后，导弹穿越突风区域时的增量平衡方程可以表示为：

(4)

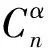
将式(1)～(3)带入式(4)，并整理得到：

(5)

式中，各项表达式如下：

由上述方程可以发现，力向量中每个元素都包含控制舵偏角Δαc的相关项，说明其对导弹刚体的沉浮运动、俯仰运动和弹性振动均有影响。

2 模型介绍

本节对导弹的结构动力学模型建模、突风空间建模和各结构/机构小系统建模分别进行介绍。

2.1 导弹模型

导弹采用梁质量块动力学模型，各分站质量以带质量的集中质量单元描述。由于弹身为连续气动外形，因此各节点处截面半径不相等，刚度单元采用变截面铁木辛克梁有限元模型，采用式(6)的型函数导数与材料参数矩阵乘积在单元长度上积分的方法，得到各单元的刚度矩阵，

(6)

2.2 突风模型

突风模型选择为“1-cos”突风模型，突风中气流速度变化与导弹飞行路径垂直，得到“1-cos”突风空间特性的表达式为：

(7)

式中，wg0为风速，Lg为突风长度，xg为导弹处在突风中的位置。

当导弹穿越突风区时，将式(7)转化为突风速度随时间的变化关系，如下式：

(8)

假设风速为40m/s，突风长度为400m，其突风速度曲线如图2所示。

图2 离散“1-cos”突风

2.3 控制模型

全弹控制模型如图3所示。在突风干扰下，弹体产生刚体动力学和弹性响应，该响应经过惯组小系统(惯组、减振器、惯组大梁组成的机械和电的复合环节)环节后，惯组敏感到弹体姿态变化，弹上计算机发出舵机运动指令，控制弹体响应。

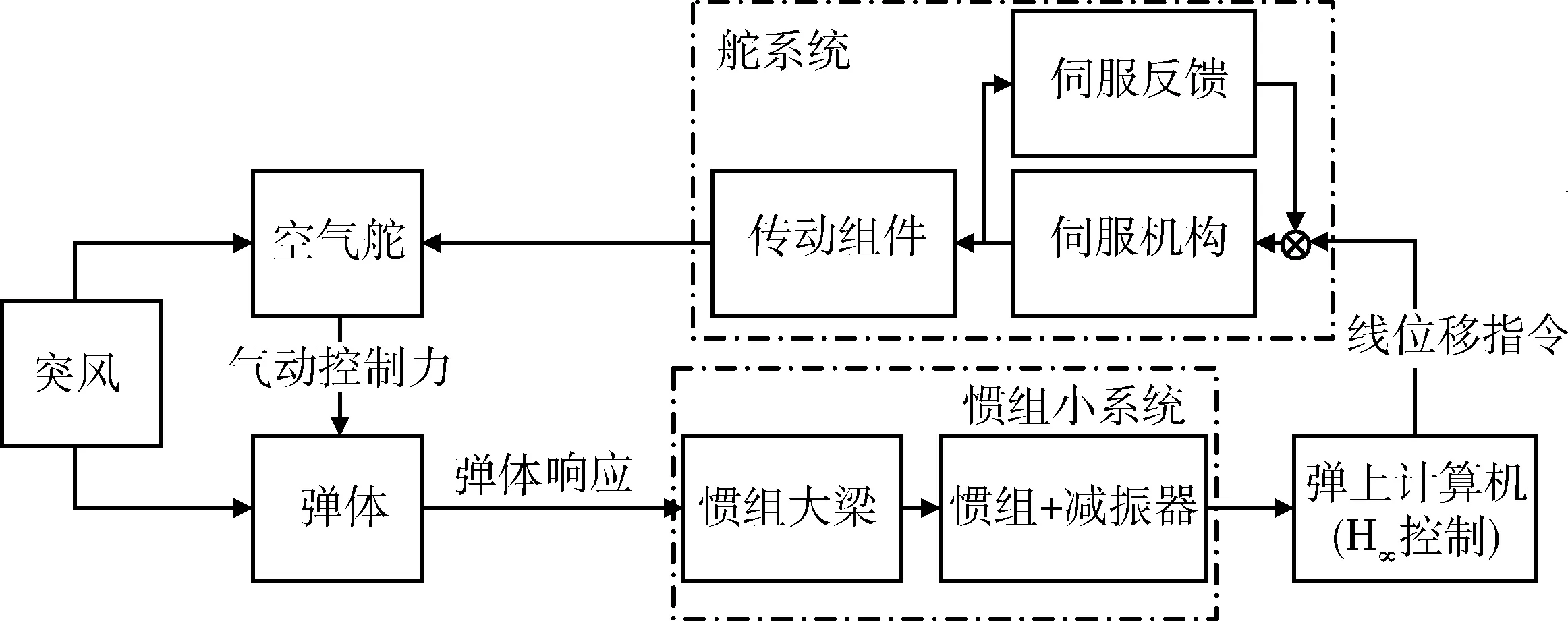
图3 全弹控制模型

其中惯组小系统角运动传递特性和舵系统(包含伺服机构、传动机构、舱体和空气舵的复合环节)角运动传递特性可通过地面试验获得，此处直接给出了其特性，幅频曲线如图4所示，相位滞后为4ms。

图4 角运动传递特性

3 H∞控制

图5给出了H∞控制框图。图中信号均为向量，W为外来输入信号；U为控制器输出，即控制器发出的控制信号；Z为调节输出，即被控输出；Y为控制输入，也称为量测输出信号，如传感器的输出或者其他能够被测量的输出信号等；G为广义被控对象；K*为控制器(其中包括控制器与状态估计器)，广义被控对象是在被控对象的基础上进行了加权增广，以加权阵去影响闭环系统的某些性能，使得设计的控制器具有鲁棒性，系统对外界扰动和建模误差都能保持鲁棒稳定。

图5 H∞闭环系统

考虑图5模型，状态空间表达式可写为：

z=C1x+D12u

y=C2x+D21w

(9)

其中：

C1=[1],C2=I6×6,D12=[06×1],D21=[I6×2],

式中,w为外部输入(包括扰动、噪声及指令信号等),u是控制输入向量,z为误差向量,y为观测向量,x为状态向量。

1)解H∞控制器的代数里卡蒂方程：

(10)

要求S∞c≥0；

2)解H∞滤波器的代数里卡蒂方程：

(11)

要求S∞e≥0；

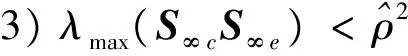
(2)闭环系统方程

(12)

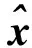
z=C0x0

(13)

其中：

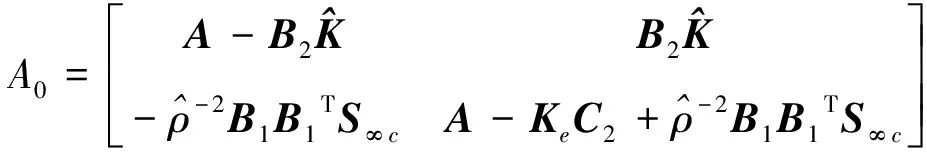
其中：

根据以上分析，计算得控制器为

计算得滤波器为

4 算例

根据导弹飞行特征数据，以导弹飞行速度最大秒点状态为例，研究该方法的可行性。导弹飞行动压220kPa，飞行速度为750m/s。根据导弹动力学参数，可以得到导弹该时刻一阶模态频率为31Hz，模态振型如图6所示。

图6 导弹一阶模态振型

将导弹相关参数带入式(9)，可以计算得到该导弹穿越突风区时有无控制下，导弹空气舵控制舵偏角曲线、惯组大梁处的角速度响应，如图7和8所示。质心处沉浮位移响应和俯仰角响应曲线如图9和10所示。

图7 导弹控制舵偏角响应

图8 导弹惯组大梁安装处角速率响应

从图7和8的计算结果可以看出，导弹在穿越“1-cos”突风时，导弹惯组大梁安装处角速率响应与突风形状一致，随着突风气流速度增大而增大，减小而减小，位移响应在0.25s时达到最大，而在0.5s穿过突风区后，由于导弹自身阻尼特性，响应逐渐衰减，但衰减效果不明显，在施加控制后其响应衰减明显。

图9 导弹质心处的沉浮位移响应

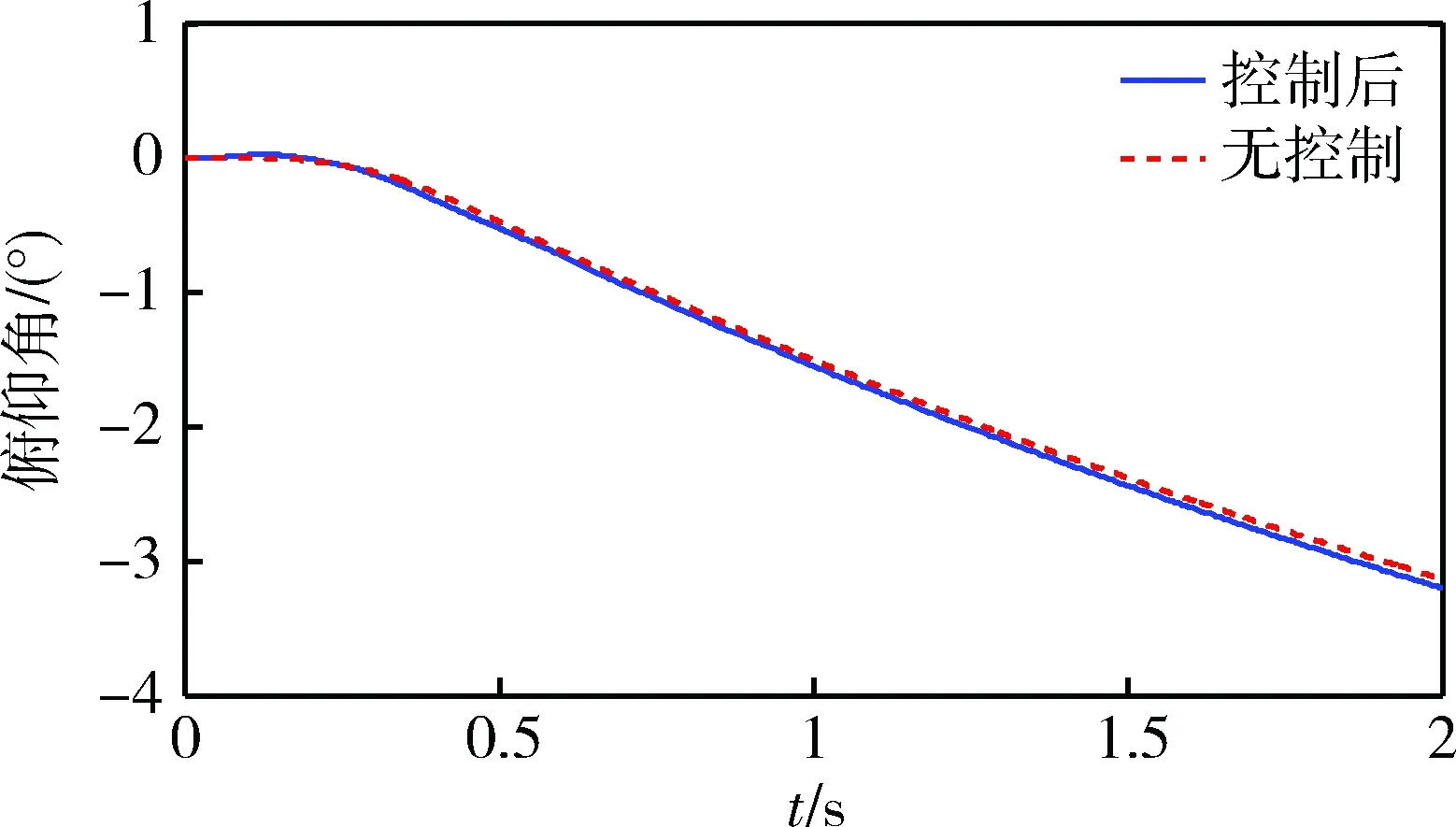
图10 导弹俯仰角响应

从图9和10可以看出，导弹在穿越突风时，质心处沉浮和俯仰角均发生了较大的响应，且响应速度在穿越突风区域后段，即0.25s后较快。施加控制后，质心处沉浮和俯仰角响应变化较小，与控制前基本相当。

5 结论

研究了战术导弹在穿越离散突风区域时，弹体的动力学响应鲁棒控制。首先，给出了导弹在穿越突风区时的运动方程，其中不仅考虑了弹体在突风区的刚体运动，而且考虑了弹体各分站位置及空气舵位置的结构动力学响应引起的附加攻角，以及突风对空气舵的滞后影响效果，另外还考虑了空气舵控制舵偏引起的控制力等。其次，建立了导弹结构动力学模型、“1-cos”突风模型和控制模型。再次，研究了弹体H∞控制方法，设计出最优控制器。最后，通过算例研究了导弹在穿越突风过程中，使用空气舵对弹体的动力学响应进行控制。

研究发现，导弹在穿越“1-cos”突风时，导弹惯组大梁安装处角速率响应与突风形状一致，随着突风气流速度增大而增大，减小而减小，而在穿过突风区后，由于导弹自身阻尼特性，响应逐渐衰减，但衰减效果不明显，在施加控制后其响应衰减明显，但质心处沉浮和俯仰角响应变化较小，与控制前基本相当。

[1] 王冬.一种细长飞行器阵风响应计算方法[J].现代防御技术, 1998, 26(4): 30-36.(WangD．NumeticalMethodforGustResponseofSlenderAircraft[J]．ModernDefenceTechnology，1998，26(4):30-36.)

[2] 徐焱. 飞机离散突风响应分析[J].飞机设计，2004, (2):11-18.(XuY．AircraftDiscreteGustResponseAnalysis[J]．AircraftDesign，2004，(2):11-18.)

[3] 张家齐.扑翼飞行器阵风响应计算与分析[D].南京:南京航空航天大学,2010.(ZhangJQ．CalculationandAnalysisofGustResponseofFlapping-wingAirVehicle[J]．Nanjing:NanjingUniversityofAeronauticsandAstronautics，2010.)

[4] 吴志刚,杨超. 弹性导弹的连续与离散阵风响应[J].北京航空航天大学学报，2007,33(2):136-140.(WuZG，YangC．ContinuousandDiscreteGustResponsesofElasticMissiles[J]．JournalofBeijingUniversityofAeronauticsandAstronautics，2007，33(2):136-140.)

[5] 杨秋艳,王育林. 飞机连续阵风载荷计算方法应用研究[J].飞行力学，2008, 26(4):65-68.(YangQY，WangYL．ResearchandApplicationoftheContinuousGustLoadsAnalysisMethodforAircraft[J]．FlightDynamics，2008，26(4):65-68.)

[6] 李山虎,杨靖波,黄清华,等. 轴向运动悬臂梁的独立模态振动控制-Ⅰ近似理论分析[J].应用力学学报，2002, 19(1): 35-38. (LiSL，YangJB，HuangQH，etal．IndependentModelSpaceVibrationControlofAnAxiallyMovingCantileverBeam-PartI:TheoreticalAnalysisofApproximation[J]．ChineseJournalofAppliedMechanics，2002，19(1):35-39.)

[7]YangKJ,HongKS,MatsunoF.BoundaryControlofaTranslatingTensionedBeamwithVaryingSpeed[J].AsmeTransactionsonMechatronics, 2005, 10(5):594-597.

[8]LiuKF,HuangT.VibrationControlofanAxially-movingCantileverBeamUsingPiezoelectricActuators[C].Proceedingsofthe11thWorldCongressinMechanismandMachineScience,Tianjin,China, 2004, 1(5): 535-539.

[9] 吴志刚,陈磊,杨超,等.弹性飞机阵风响应建模与减缓方案设计[J].中国科学:技术科学,2011,41(3):394-402.(WuZG，ChenL，YangC,etal．GustResponseModelingandAlleviationSchemeDesignforanElasticAircraft[J]．ScienceChinaTechnologicalSciences，2011，41(3):394-402.)

[10] 曹九发.飞机阵风响应仿真计算及载荷减缓技术研究[D].南京:南京航空航天大学,2010.(CaoJF．SimulationCalculationofAircraftGustResponseandResearchonLoadsAlleviation[J]．Nanjing:NanjingUniversityofAeronauticsandAstronautics，2010.)

Study on the Discrete Gust Dynamic Response and Robust Dynamic Control of Tactics Missile

Zhao Changjian1， 2, Wang Hongbo1， 2, Liao Xuanping1， 2, Wang Liang2

1. College of Aerospace Science and Engineering, National University of Defense Technology, Changsha 410073, China; 2. China Academy of Launch Vehicle Technology, Beijing 100076, China

Whenthetacticsmissilefliesacrossthediscretegust,therobustdynamiccontrolofthemissileareinvestigated.Thekinematicsequationsandstructuredynamicmodelofthemissilearederivedand‘1-cos’gustmodelandthecontrolmodelareestablished,therefore,theinfluenceofstructuredynamicontheadditionalangle-of-attackofallkeysectionandairhelm，thelageffectofthediscretegusttoairhelmandthecontrolforceofairhelmaretakenintoaccount.ThedynamicresponseandthecontrolofthemissilearestudiedbycasestudyinwhichtheH∞controlstrategyofthemissileisstudiedandtheoptimalcontrolleraredesigned.Theresultsofstudyshowthatthedynamicresponseofthemissileisobviouslydecayingwhenthecontrolworks.

Vibration；Mode；Discretegust；H∞control；Missile

2015-08-05

赵长见(1976-)，男，河南人，博士研究生，研究员，主要从事飞行器总体设计；王洪波(1972-)，男，黑龙江人，博士研究生，研究员，主要从事飞行器总体设计；廖选平(1977-)，男，四川人，博士研究生，研究员，主要从事飞行器总体设计；王 亮(1985-)，男，江苏人，博士，高级工程师，主要从事飞行器载荷与环境设计。

O32

A

1006-3242(2016)04-0016-07