一种基于前斜视成像的自适应末制导律设计方法
梁 卓 赵长见 周国峰 王丽华 潘彦鹏
中国运载火箭技术研究院,北京 100076
一种基于前斜视成像的自适应末制导律设计方法
梁 卓 赵长见 周国峰 王丽华 潘彦鹏
中国运载火箭技术研究院,北京 100076

由于末制导飞行段飞行器全程在大气层内飞行,飞行弹道极易受到气动偏差和风干扰等影响,导致末制导初始条件具有较大的不确定性。针对该问题,推导了前斜成像条件下,前斜角与航迹偏航角、视线方位角之间的几何关系模型,在此基础上,提出了前斜成像条件下的自适应末制导律设计方法,并通过数学仿真证明了该方法的正确性和可行性。
斜视成像;前斜角;自适应末制导律
为提高飞行器对目标探测识别的距离和能力,飞行器采用雷达成像导引头进行末制导,即在飞行末端采用斜视成像制导模式。而斜视成像末制导技术的关键是设计合理的制导律,确保斜视条件成立,即保证成像时飞行器具有足够大的前斜角[1-3]。而实战环境下,一方面,飞行器飞行时受到各种偏差和干扰的影响,弹道具有较大的不确定性;另一方面,目标机动亦具有一定的不确定性。因此,采用何种导引方式达到实时生成弹道满足斜视成像条件,并且在成像完成后调整弹道将飞行器精确导向目标是一项亟待攻克的技术难题[4-5]。
为此,首先从前斜角的定义出发,推导前斜角与航迹偏航角和视线方位角的几何关系模型,提出了前斜成像条件下的自适应末制导律设计方法,为航迹具有一定约束条件的成像末制导律设计提供了参考。
1 前斜视成像约束建模
前斜成像的条件是对飞行器飞行轨迹进行规划,确保成像时刻速度矢量与弹目视线在水平面内的投影之间的夹角绝对值,即前斜角不小于给定值,并在成像过程中保持不变。成像完成后,再由制导律将飞行器重新导向射面。图1示意了斜视成像末制导过程中在水平面内的几何关系,其中A点为末制导起点,B点为成像起点,C点为成像结束点,T点为目标点,η为前斜角,V为速度矢量。
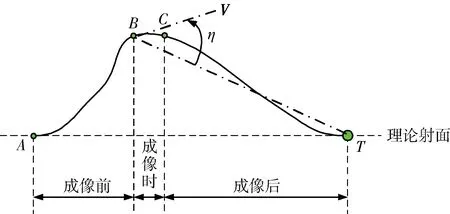
图1 斜视成像末制导过程中在水平面内的几何关系示意图
图2为弹目几何关系示意图,M为飞行器,T为目标,M′为飞行器在发射坐标系O-xyz的xoz平面上的投影,M′-xyz与发射坐标系相应各轴平行,T-xtytzt为x轴指向发射点的目标坐标系。航迹偏航角、前斜角、发射坐标系与发射视线系之间的方位视线角、目标坐标系与目标视线系之间的方位视线角之间具有如下几何关系:
η=σ-qz=σ-q1z
(1)

图2 弹目几何关系示意图
2 自适应末制导律设计
末制导律包括纵向制导律和航向制导律,纵向末制导律设计采用有落角约束的最优比例导引律;航向制导律设计成像前采用角度跟踪控制,成像结束后采用比例导引律将飞行器导向目标。
2.1 纵向末制导律设计
纵向末制导律采用有落角约束的最优比例导引律,具体参见文献[6],本文直接给出结果,纵向指令过载
(2)
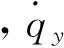
2.2 航向末制导律设计
为确保前斜角满足成像条件,采用角度跟踪控制,跟踪在线实时生成的理想前斜角曲线,实现在各种偏差和干扰条件下,前斜角在设定时刻到达期望值,之后在成像需用时间内前斜角保持不变,完成成像后转入比例导引控制,将飞行器导向目标。由于导引头成像前后航向末制导律的设计目标不同,以下分别进行设计。
2.2.1 成像前制导律
成像前航向制导律设计包括2个环节:1)在线生成理想前斜角曲线;2)设计基于角度闭环控制的自适应控制律跟踪理想前斜角,具体实现如下:
1)在线生成理想前斜角曲线
采用基于3次曲线拟合的方法建立成像前理想前斜角模型,并由起点约束与终点约束条件确定相关参数,从而实时给出理想前斜角与前斜角变化率随时间的变化曲线,作为角度跟踪控制的输入参考基准。理想前斜角模型的推导结果如下。

ηc=k3t3+k2t2+k1t+k0
(3)
(4)
由此得到前斜角和前斜角变化率随时间的变化率为
(5)
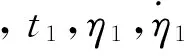

NB:负大;NM:负中;NS:负小;ZR:零;PS:正小;PM:正中;PM:正大。


表1 模糊控制规则表
解模糊化方法采用重心法,模糊控制器输出变量为
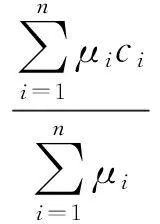
(6)
式中,μi为第i条模糊规则的隶属度;n=49,为模糊控制规则总数。
2)基于角度跟踪闭环控制的自适应成像前飞行段制导律设计
基于前斜角跟踪控制的制导律指令形成框图如图1所示。采用以前斜角偏差、前斜角偏差积分量和前斜角偏差导数为状态量,以横向过载为控制量的闭环末制导律。
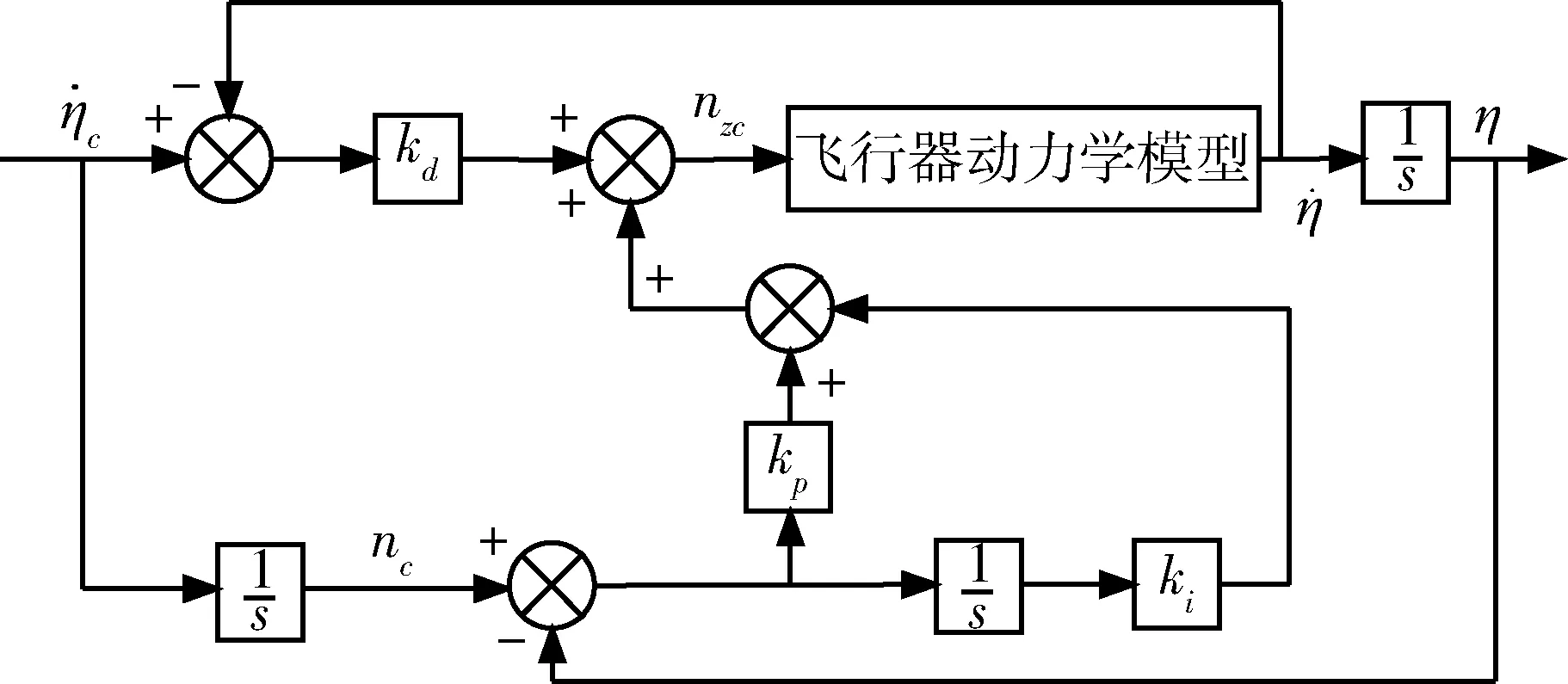
图3 基于前斜角跟踪控制的制导律指令形成框图
通过时域和频域仿真确定出PID控制相关参数kp,ki和kd。由此,得到成像前航向制导律为
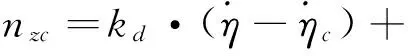
(7)
式中,nzc为航向指令过载。
2.2.2 成像过程中的制导律
成像过程中的航向制导律设计同样包括2个环节:1)在线生成理想前斜角曲线;2)设计基于角度闭环控制的自适应控制律跟踪理想前斜角,具体实现如下。
1)在线生成理想前斜角曲线
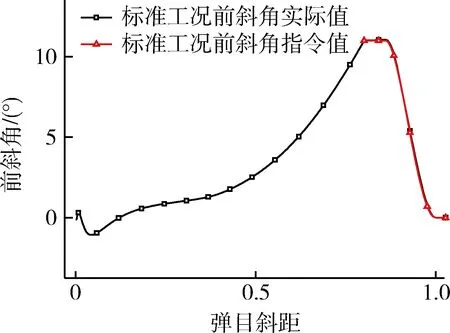
ηc=η2(t2 (8) 其中,需用成像时间Δt与前斜角η2成反比。 2)基于角度跟踪闭环控制的自适应成像前飞行段制导律设计 (9) 2.2.3 成像后制导律 成像完成后采用比例导引将飞行器导向目标,航向指令过载为 (10) 为考核本文所提方法的有效性,分别在标准工况和在组合偏差和干扰条件下,对末制导律进行数学仿真分析。仿真时假设斜视成像条件为前斜角11°,保持2s,主要参数曲线如图4~8所示(图中曲线除角度外,其它物理量均进行了归一化处理)。其中,图4给出了前斜角随弹目斜距的变化曲线,图5和6分别给出了标准工况和干扰工况下前斜角实际值与指令值随弹目斜距的变化曲线,图7给出了横向位置随弹目斜距的变化曲线,图8给出了当地弹道倾角随弹目斜距的变化曲线。 图4 前斜角随弹目斜距的变化曲线 图5 标准工况下前斜角实际值与指令值随弹目斜距的变化曲线 图6 干扰工况下前斜角实际值与指令值随弹目斜距的变化曲线 图7 横向位置随弹目斜距的变化曲线 图8 当地弹道倾角随弹目斜距的变化曲线 由以上仿真结果可以看出,在标准工况和在组合偏差和干扰条件下: 1)前斜角能可靠地跟踪在线生成的理想前斜角曲线,且在成像时刻前斜角均能满足斜视成像11°的要求; 2)末制导律能有效保证末端弹道倾角满足约束要求,末端横向位置均能精确地控制至射面内。 首先从前斜角的定义出发,建立了前斜角与航迹偏航角和视线方位角的几何关系模型,提出的以前斜角偏差、前斜角偏差变化率和前斜角偏差积分为状态量,以横向过载为控制量的末制导律可自适应保证前斜成像条件的成立,有效解决了对航迹具有一定约束条件的成像末制导律的设计问题。同时该方法简单、自适应性强,具有工程应用价值。 [1] 孟自强,李亚超,汪宗福,等.弹载双基前视SAR俯冲段弹道设计方法[J].系统工程与电子技术, 2015,37(4):768-774.(MengZiqiang,LiYachao,WangZongfu,etal.DesignMethodofMBFL-SARTrajectoryDuringTerminalDivingPeriod[J].SystemsEgineeringandElectronics,2015,37(4):768-774.) [2] 王阳阳.弹载前斜视成像技术研究[D].哈尔滨:哈尔滨工业大学, 2014.(WangYangyang.ResearchonMissile-borneForwardSquintSyntheticApertureRadarImagingTechnology[D].Harbin:HarbinInstituteofTechnology,2014.) [3]ShinHS,LimJL.RangeMigrationAlgorithmforAirborneSquintModeSpotlightSARImaging[C].IETRadar,Sonar&Navigation, 2007, 1(1):77-82. [4] 谢华英,范红旗,赵宏钟,等.SAR成像导引头的弹道设计与优化[J].系统工程与电子技术,2010,32(2):333-337.(XieHuaying,FanHongqi,ZhaoHongzhong,etal.TrajectoryDesignandOptimizationforaSARSeeker[J].SystemsEngineeringandElectronics,2010,32(2):333-337.) [5] 朱学平,杨军,刘俊,等.一种SAR成像制导导弹制导律研究[J].测控技术, 2009,28(9):69-71.(ZhuXueping,YangJun,LiuJun,etal.StudyofaGuidanceLawforSARImageGuidedMissiles[J].Measurement&ControlTechnology,2009,28(9):69-71.) [6] 梁卓,雷延花,韩英宏,等.基于单边攻角特性的吸气式飞行器下压制导律设计与仿真[J].航天控制, 2014, 32(5):36-39.(LiangZhuo,LeiYanhua,HanYinghong,etal.DesignandSimulationofaDrivingDown-PhaseGuidanceLawforAir-BreathingVehiclesBasedonSingleAttackAngleCharacteristics[J].AerospaceControl,2014,32(5):36-39.) Design of A Squint Imaging Adaptive Terminal Guidance Law Liang Zhuo, Zhao Changjian,Zhou Guofeng,Wang Lihua,Pan Yanpeng China Academy of Launch Vehicle Technology,Beijing 100076,China Duringflyingintheatmosphereatthestageofterminalguidancephase,theair-breathingvehicleisliabletobeaffectedbythewindageofaerodynamicforce,windandotherfactors,whichenhancestheuncertaintyofinitializationofvehicles.Aimingatsolvingthisproblem,ageometricrelationmodelisfirstlydeducedamongtheheadingangle,trajectorydeflectionangleandazimuthangle,andthenasquintimagingadaptiveterminalguidancelawisproposed.Andthevalidityandfeasibilityofthemethodaretestifiedbythesimulation. Squintimaging;Headingangle;Adaptiveterminalguidancelaw 2015-11-10 梁 卓(1982-),男,陕西汉中人,博士,高级工程师,主要从事飞行器制导与控制技术研究;赵长见(1976-),男,河南信阳人,硕士,研究员,主要从事飞行器控制技术研究;周国峰(1982-),男,湖北荆州人,硕士,高级工程师,主要从事飞行器制导与控制技术研究;王丽华(1973-),女,山东烟台人,硕士,研究员,主要从事飞行器控制技术研究;潘彦鹏(1984-),男,甘肃定西人,博士,工程师,主要从事飞行器制导与控制技术研究。 TJ765 A 1006-3242(2016)03-0046-05
3 仿真算例与分析

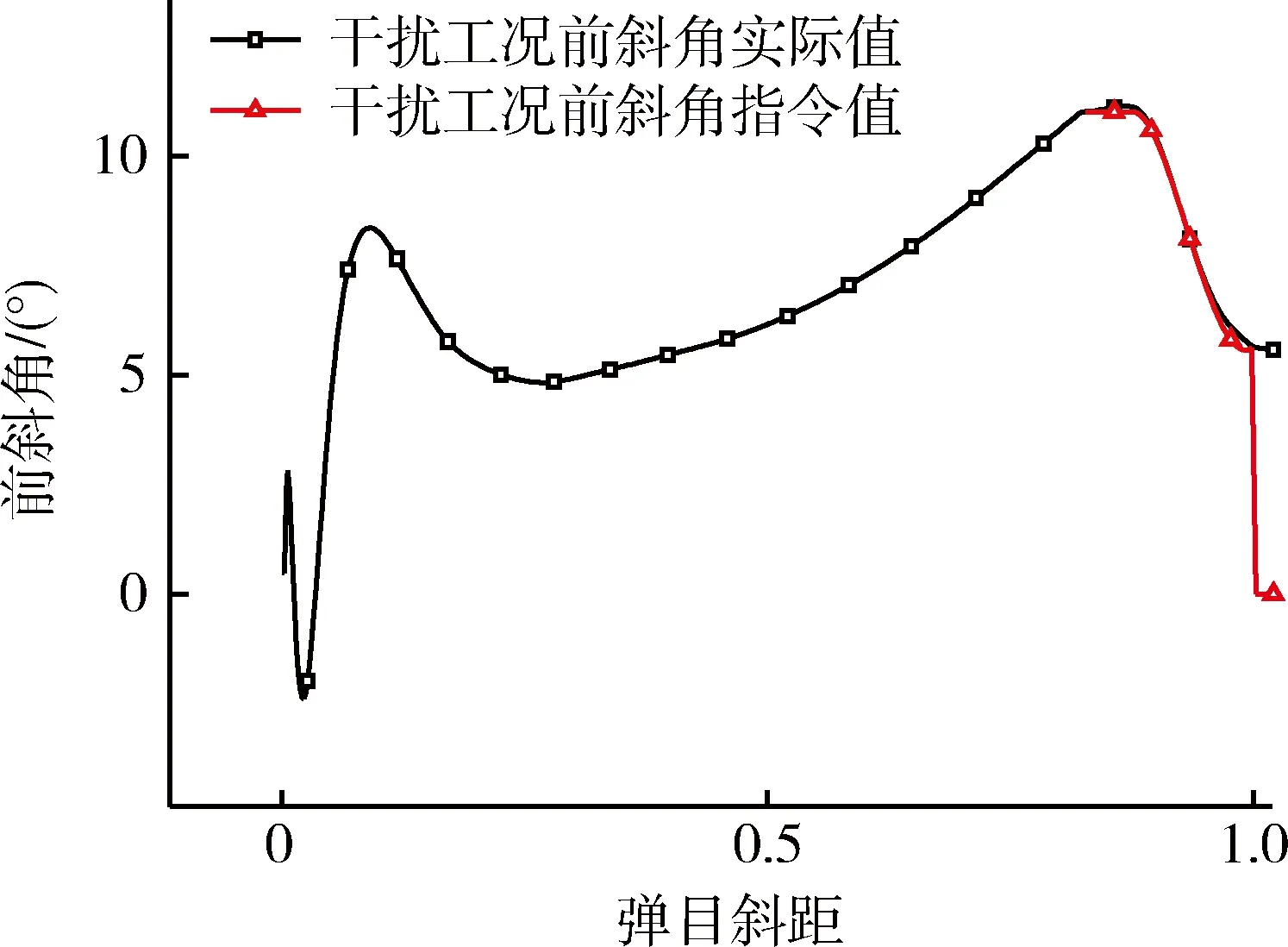
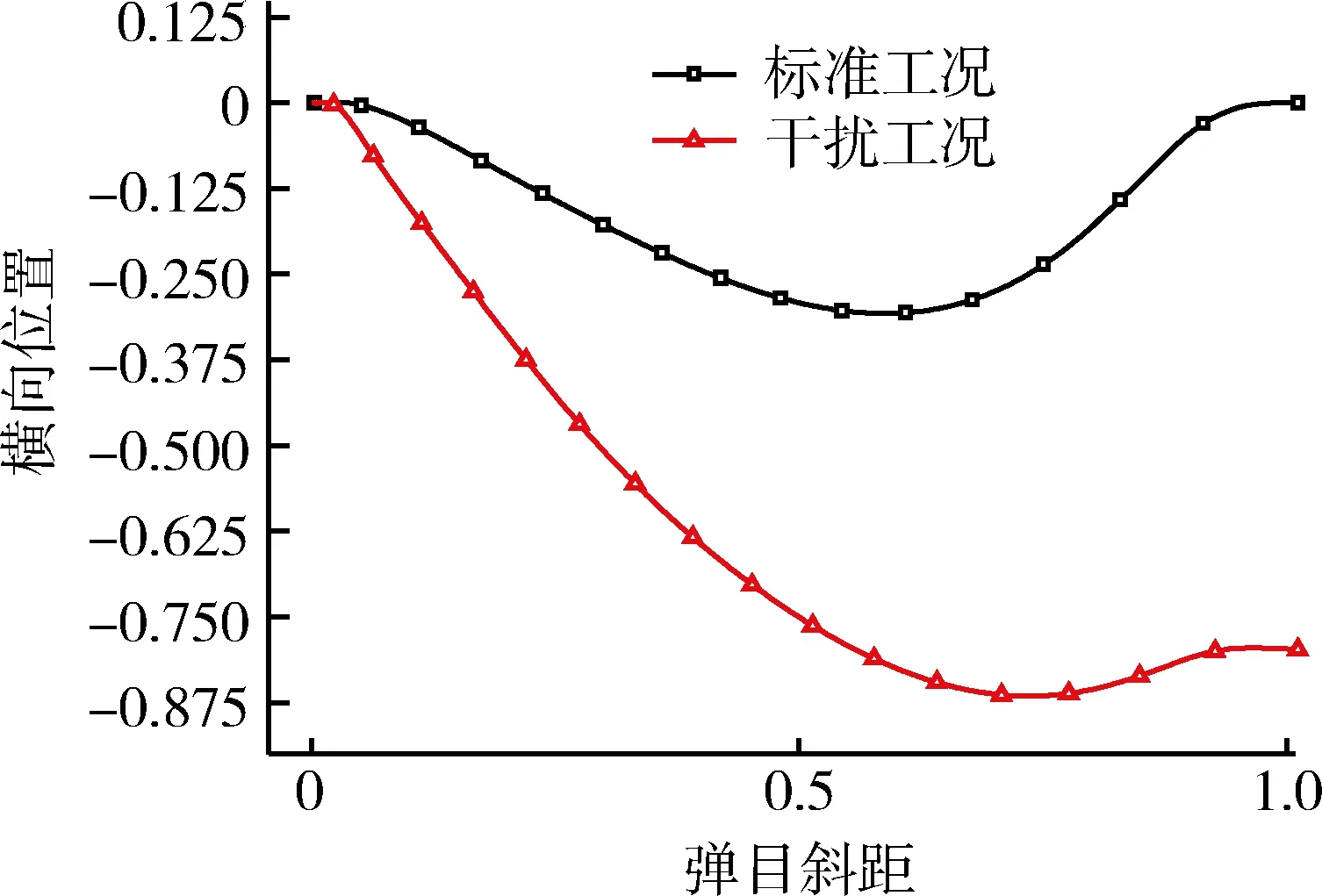

4 结论

