基于FAHP法钢箱梁斜拉桥主梁施工方案比选

郭廷泰, 韩晓虎, 安平和, 贺　攀

(1. 中国水电建设集团 路桥工程有限公司, 北京　100048; (2. 中国水利水电第三工程局有限公司, 陕西 西安　710016; (3. 长安大学 公路学院, 陕西 西安　710064)



基于FAHP法钢箱梁斜拉桥主梁施工方案比选

郭廷泰1, 韩晓虎2, 安平和3, 贺攀3

(1. 中国水电建设集团 路桥工程有限公司, 北京100048; (2. 中国水利水电第三工程局有限公司, 陕西 西安710016; (3. 长安大学 公路学院, 陕西 西安710064)

摘要:建立钢箱梁斜拉桥主梁施工方案优化排序的数学模型,对西安富裕路沣河大桥3种施工备选方案进行比选.通过实地调研和文献查阅完成专家调查表.因FAHP考虑了人脑决策时的模糊性,可以提高结果的客观和准确程度,故采用FAHP法计算各备选方案的权重,最终确定选择最优施工方案.

关键词:FAHP; 钢箱梁; 斜拉桥; 施工方案比选

斜拉桥因其良好的受力性能、强大的跨越能力,以及索和塔可以组合出很多优美外形来满足景观上的要求,因此,其成为现代桥梁工程中发展最快、最具竞争力的桥型之一[1].钢箱梁斜拉桥建设投资大、建造工期长、所处的环境复杂,而钢箱梁作为结构的主要组成部分,其施工更具特殊性[2].影响钢箱梁斜拉桥主梁施工方案选择的因素众多,既有能够定量描述的因素,也有只能定性而不能定量描述的因素,以及一些不可预见的因素,这些将使主梁施工方案的选择具有极大的模糊性,它的推理和判断大多是模糊推理和模糊判断,因而是一个涉及多层次、多因素、多目标、多指标的模糊决策过程[3].实际上,人们在处理复杂的决策问题时常常不自觉地应用模糊判断,特别是在动态、不确定性的环境下更是需要模糊决策.因此,本文拟采用模糊层次分析法(FAHP法),对西安富裕路沣河大桥钢箱梁斜拉桥主梁施工方案评价进行量化选择.

1模糊层次分析法的综合评价模型

1.1模糊层次分析法的原理

众多的决策方法中,层次分析法(AHP)拥有定性和定量相结合处理各种评价因素的特点.由于其理论上具有完备性,结构上具有严谨性,解决问题上具有简洁性,尤其在解决非结构化决策问题上具有明显的优势,因此在各行各业得到了广泛应用[4].但是当用层次分析法分析某一层次评价指标很多时(如4个以上),其思维一致性很难保证,而且人脑判断具有模糊性,而将模糊理论与传统层次分析法相结合、充分考虑人思考的模糊性形成的模糊层次分析法(FAHP),能很好地解决这一问题[5].目前,模糊层次分析法分为两大类,一类是基于模糊数的模糊层次分析法,另一类是基于模糊一致矩阵的模糊层次分析法.本文选用一种基于三角模糊数互补判断矩阵的方法,来进行钢箱梁斜拉桥主梁施工方案比选.

1.2基于FAHP的施工方案比选指标权重系数确定

依据模糊层次分析法的基本理论与步骤,逐步完成钢箱梁斜拉桥主梁各施工方案权重系数的确定.

(1) 建立FAHP层次结构模型.由于斜拉桥钢箱梁施工方案的影响因素众多,主梁施工工艺复杂,施工难度大,因此主梁施工方案的选择不仅要考虑技术可行性和经济合理性,同时要考虑工程建设和主梁施工对周围环境的影响以及产生风险事故的可能性.一般工程对施工工期有严格要求,因此,施工工期也成为评价主梁施工方案优劣的指标之一.选择施工难易度、风险损失度、施工安全性、工程造价、工程进度、对周边环境的影响等6个指标来评价方案的优劣,构建层次结构模型如图1所示.

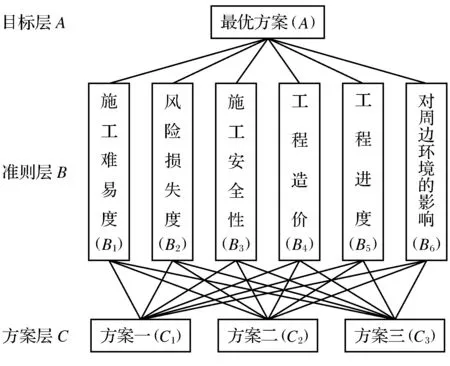
图1　层次结构模型

(2) 构造模糊判断矩阵.专家组利用模糊数来表达他们的意见.假设有n个专家,他们对一组指标进行比较(比如Bi与Bj的比较),各自得到一个模糊数,分别为(l1,m1,u1),(l2,m2,u2),…,(ln,mn,un)[6].将n个模糊数通过取均值整合成一个,记为αij,即

重复以上步骤,直到所有的比较变成一个模糊数.

(4) 将所有模糊数去模糊化.M1(l1,m1,u1)和M2(l2,m2,u2)是三角模糊数.M1>M2的可能度用三角模糊函数定义为[7]:

一个模糊数大于其他K个模糊数的可能度,被定义为:

minP(M≥Mi)=a

minP(M≥Mi)=b

minP(M≥Mi)=c

将以上权重值标准化,得到各指标的最终权重.

(5) 相对于若干个目标层,就可按上述步骤得到若干个准则层模糊权重矩阵

(6) 对于若干个准则层也可按照上述步骤得到若干个准则层模糊权重矩阵

(7) 将针对各准则的方案层的最终权重与准则层的最终权重对应相乘得到方案的最终得分.

2FAHP法应用实例分析

2.1工程概况

西安富裕路沣河大桥位于西安市沣渭新区中南部,跨越沣河.孔跨布置为(38+36+36+35)m+(80+80)m+(35+35+35)m+(35+35+38)m,桥梁全长525.16m.其中主桥为单塔“花瓣式”钢拱塔斜拉桥,长度为80m+80m,宽度为23.5×2=47.0m,全桥重约7 109t.本桥主梁采用钢箱梁单箱多室结构形式,梁高1.8m.钢拱塔外观呈斜伸的双网球拍型,与竖直方向立面约呈1∶2.5的倾斜角,塔高约53.178m,其中桥面标高以上部分高39.028m.大桥效果图见图2.

图2　主桥效果图

2.2施工备选方案

2.2.1少支架施工

在应铺设桥面板的相应位置打入临时钢管墩柱,并在柱顶铺设贝雷梁[8].贝雷梁铺设完成后,在其上完成主梁的吊装、焊接及张拉斜拉索等工作.其施工示意如图3所示.

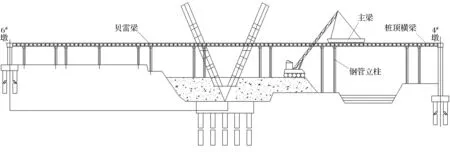
图3　少支架法施工图

2.2.2悬臂拼装施工

悬臂拼装法由桥塔处的零号块逐个向两边悬臂拼装.采用大吨位吊机将分块的主梁起吊至拼装位置后人工焊接,等其与之前拼装好的主梁拼装成桥后张拉斜拉索,重复上述步骤直至成桥[9].其施工示意见图4.

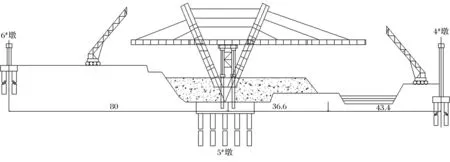
图4　悬臂拼装施工图

2.2.3顶推施工

顶推施工法是在沿桥纵轴方向的后方设置预制场地,分节段或全部预制梁体,并将预制节段与已经施工完成的梁体连为整体,通过水平千斤顶施力,将梁体向前顶推离开预制场地逐步行至成桥位置,然后继续在预制场地进行下一节段梁体的预制,如此循环操作,直至施工完成[10-11].其施工示意如图5所示.

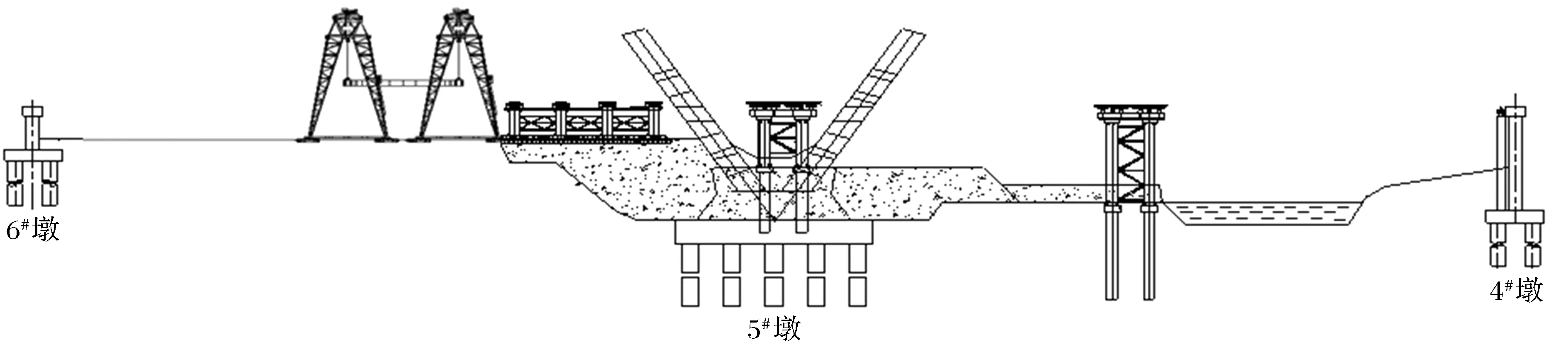
图5　顶推施工图

2.3构建专家意见调查表

在查阅国内外类似桥梁的文献资料及对施工现场调查的基础上,本文综合了10位桥梁施工方面相关专家的意见,整理出专家意见调查表(见表1),为随后构建判断矩阵提供依据.

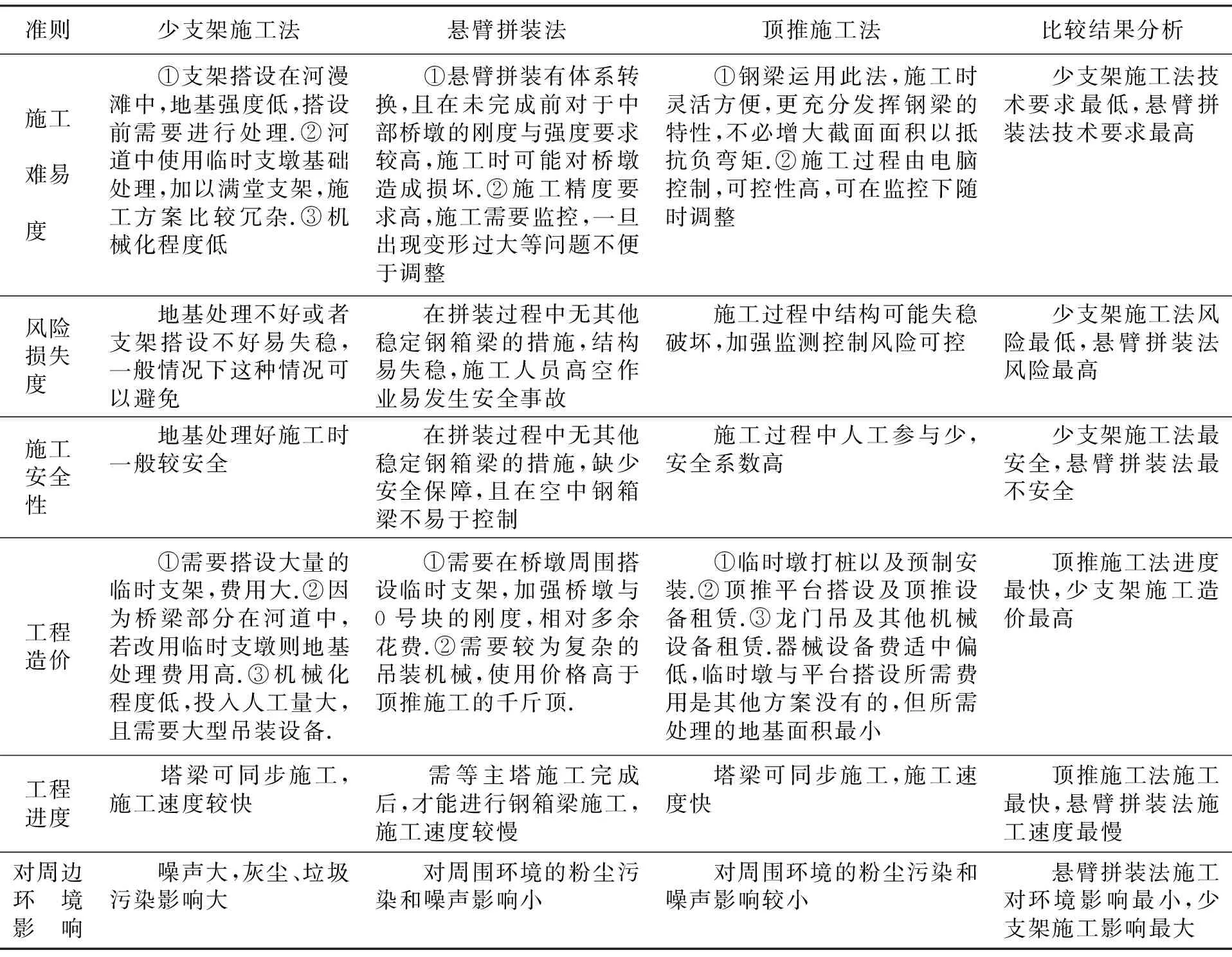
表1　专家意见调查表

2.4计算分析并选择最终方案

构造目标层-准则层判断矩阵并检验.通过对专家及相关从业人员问卷调查,要求被调查者依照“0.1～0.9标度表”对各准则进行两两比较并打分,得出三角模糊值(l,m,u),其中l为相比较下重要程度的下界,m为相比较下重要程度的中值,u为相比较下重要程度的上界,最终形成判断矩阵并进行一致性检验,见表2.

表2　0.1～0.9数量标度

表3　目标层准则层分析优化矩阵A～Bi

D(B1)=(0.140,0.179,0.223)

D(B2)=(0.118,0.147,0.184)

D(B3)=(0.137,0.165,0.202)

D(B4)=(0.164,0.196,0.231)

D(B5)=(0.158,0.187,0.223)

D(B6)=(0.101,0.126,0.156)

P(Dc1≥Dci)=0.780P(Dc2≥Dci)=0.290

P(Dc3≥Dci)=0.551P(Dc4≥Dci)=1.000

P(Dc5≥Dci)=0.868P(Dc6≥Dci)=0.225

得到准则层最终权重(0.210,0.078,0.148,0.269,0.234,0.061).

再通过对专家及相关从业人员问卷调查,要求被调查者依照“1～9标度表”对C层各施工方法进行两两比较并打分,得出三角模糊值(l,m,u).其中方案1(C1)为少支架施工法,方案2(C2)为悬臂拼装法,方案3(C3)为顶推施工法,所得矩阵见表4～表9.

表4　“施工难易度”对方案层的判断矩阵B1～C

计算方法同上,得到方案层“施工难易度”最终权重(0.453,0.217,0.330).

表5　“风险损失度”对方案层的判断矩阵B2～C

得到方案层最终权重(0.623,0.022,0.355).

表6　“施工安全性”对方案层的判断矩阵B3～C

得到方案层最终权重(0.422,0.205,0.373).

表7　“工程造价”对方案层的判断矩阵B4～C

得到方案层最终权重(0.137,0.363,0.501).

表8　“工程进度”对方案层的判断矩阵B5～C

得到方案层最终权重(0.142,0.376,0.482).

表9　“对周围环境的影响”对方案层的判断矩阵B6～C

得到方案层最终权重(0.201,0.440,0.359).

将针对各准则的方案层的最终权重与准则层的最终权重对应相乘得到3个方案的最终得分(0.288 5,0.290 1,0.421 7).

2.5比选方案分析

(1) 基于模糊层次分析决策理论,根据钢箱梁斜拉桥施工特点和城市建筑环境特性,选取6个指标建立了钢箱梁斜拉桥主梁施工方案综合评价指标体系,构造出主梁施工方案优选的评价与决策模型.

(2) 施工难易度、工程造价、工程进度和施工安全性4个准则对于沣河大桥钢箱梁施工方案的选择影响较大.

(3) 用层次分析法和模糊数学理论建立模糊综合评判模型对西安富裕路沣河大桥进行实例分析,得出方案集的综合评判:少支架法0.288 5,悬臂拼装法0.290 1,顶推施工法0.421 7,从而选择顶推施工,为实际工程建设提供决策依据.

(4) 通过计算分析可知,顶推施工法最具可行性.从具体实践来看,这一结果也具备充分的合理性:沣河大桥地处西安市郊区,远离城市繁华地段,具有充足的作业空间,顶推施工难度和建造成本低、施工速度快、安全性好,故而最为合理.

3结语

层次分析法是一种综合分析方法,运用层次分析法可以确定具体的评价指标体系和各级指标的权重,减少传统上确定权重过程中的主观随意成分,使得评价结果客观公正,有较高的可信度,相信该方法在评价等各方面将有更广泛的应用[1].在其他桥梁施工方案比选过程中,可以根据桥梁所处的具体社会和自然环境重新确定准则层各因素的权重,同时根据各施工方法的特点选择方案层的备选方案进行方案比选;在比选过程中应该丰富受访专家的层次结构和数量,进而提高判断矩阵的充分性和客观性.

参考文献:

[ 1 ] 艾国柱. 斜拉桥通鉴[M]. 成都:西南交通大学出版社, 2011:4-12.

(AIGZ.Cable-stayedbridgegeneralappreciation[M].Chengdu:SouthwestCommunicationUniversityPress, 2011:4-12.)

[ 2 ] 陈明宪. 斜拉桥的发展与展望[J]. 中外公路, 2006,26(4):76-86.

(CHENMX.Developmentandprospectofcablestayedbridge[J].JournalofChinaandForeignHighway, 2006,26(4):76-86.)

[ 3 ] 宋帅. 基于模糊多属性群决策的桥梁建设方案比选应用研究[D]. 重庆:重庆交通大学, 2009.

(SONGS.Selectionapplicationofbridgebuildingmodelbasedongroupdecision-makingoffurrymulti-attribute[D].Chongqing:ChongqingCommunicationUniversity, 2009.)

[ 4 ] 刘莹昕,刘飒,王威尧, 层次分析法的权重计算及其应用[J]. 沈阳大学学报(自然科学版), 2014, 26(5): 372-375.

(LIUYX,LIUS,WANGWY.ComputationofweightinAPHanditsapplication[J].JournalofShenyangUniversity(NaturalScience), 2014,26(5):372-375.)

[ 5 ] 邱训兵. 多目标决策方法在桥梁施工方案比选中应用的探讨[J]. 中外公路, 2006,26(1): 105-108.

(QIUXB.Discussionontheapplicationofmultiobjectivedecisionmethodinbridgeconstructionschemeselection[J].JournalofChinaandForeignHighway, 2006,26(1):105-108.)

[ 6 ] 张吉军.模糊层次分析方法(FAHP)[J]. 模糊系统与数学, 2000,14(2):80-88.

(ZHANGJJ.Fuzzyanalytichierarchyprocess(FAHP)[J].FuzzySystemsandMathematics, 2000,14(2):80-88.)

[ 7 ] 吕跃进. 基于模糊一致矩阵的模糊层次分析法的排序[J]. 模糊系统与数学, 2002,16(2): 79-85.

(LYUYJ.Rankingoffuzzyanalytichierarchyprocessbasedonfuzzyconsistentmatrix[J].FuzzySystemsandMathematics, 2002,16(2):79-85.)

[ 8 ] 何畏,唐亮,强士中,等. 大跨度焊接钢箱梁斜拉桥施工控制技术研究及应用[J]. 桥梁建设, 2002(5):14-18.

(HEW,TANGL,QIANGSZ,etal.Theresearchandapplicationofcontroltechniqueforconstructionoflongspanweldingsteelboxgirdercablestayedbridge[J].BridgeConstruction, 2002(5):14-18.)

[ 9 ] 罗建华,付润生. 桥梁施工技术[M]. 成都:西南交通大学出版社, 2009:291-304.

(LUOJH,FURS.Bridgeconstructiontechnology[M].Chengdu:SouthwestCommunicationPress, 2009:291-304.)

[10] 姚玲森. 桥梁工程[M]. 北京:人民交通出版社, 2008:483-488.

(YAOLS.Bridgeengineering[M].Beijing:ChinaCommunicationPress, 2008:483-488.)

[11] 李亚东. 桥梁工程概论[M]. 成都:西南交通大学出版社, 2006:220-230.

(LIYD.Bridgeengineeringintroduction[M].Chengdu:SouthwestCommunicationUniversityPress, 2006:220-230.)

【责任编辑: 祝颖】

ConstructionPlanningDecisionofSteelBoxGirderBridgeBasedonFAHPMethod

Guo Tingtai1, Han Xiaohu2, An Pinghe3, He Pan3

(1.Road&BridgeEngineeringCompany,ChinaHydropowerConstructionGroup,Beijing100048,China; 2.SinohydroBureau3Co.,Ltd.,Xi’an710016,China; 3.SchoolofHighway,Chang’anUniversity,Xi’an710064,China)

Abstract:The construction optimization mathematical model of the steel box girder of cable-stayed bridge is established to make comparison of the three kinds of construction alternatives of Xi’an Fenghe Bridge. Through on site investigation and literature materials consulting to complete the exporters’research charts, using FAHP method to calculate the weight of each alternative option, and the optimum construction scheme is finally determined.

Key words:FAHP; steel box girder; cable stayed bridge; comparison and selection of construction schemes

文章编号:2095-5456(2016)03-0237-07

收稿日期:2016-03-02

作者简介:郭廷泰(1974-),男,陕西西安人,中国水电建设集团路桥工程有限公司工程师.

中图分类号:U 443.3

文献标志码:A