随机二阶锥规划问题的快速空间分解方法

陆　媛

(沈阳大学 师范学院, 辽宁 沈阳　110044)



随机二阶锥规划问题的快速空间分解方法

陆媛

(沈阳大学 师范学院, 辽宁 沈阳110044)

摘要:讨论了基于空间分解的随机二阶锥规划问题的样本均值近似方法(简称SAA方法),在适当的条件下,证明了SAA问题的解以概率1收敛到原问题的解,并且随着样本容量的增加收敛速度是指数的. 基于分解理论,给出了SAA问题的超线性收敛算法框架.

关键词:随机优化; 二阶锥规划; 样本均值近似; 空间分解; 超线性收敛

考虑如下的随机二阶锥规划(SSOCP)问题

(1)

m+1维的二阶锥定义如下:

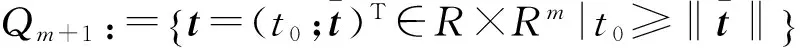
由Qm+1诱导的序关系Qm+1定义如下

本文讨论SSCOP(1)问题的样本均值近似方法(SAA). Shapiro在文献[1]中讨论了随机广义方程的SAA方法,亦可参见文献[2-6]. SAA方法的基本思想是由蒙特卡罗模拟产生独立同分布的样本,并且使用函数的样本均值来近似代替目标函数,然后利用确定型优化方法求解SAA问题,最后得到原始问题的近似解.

令ξ1,ξ2,…,ξN和η1,η2,…,ηN分别是随机变量ξ和η的样本. 问题(1)的SAA问题如下

(2)

称问题(2)是SAA问题,(1)为原问题.

本文的结构如下:首先问题(2)通过精确罚函数被转化为无约束问题,然后在浩斯道夫距离的意义下证明了近似解集收敛到原问题的解集.给出SAA问题的分解理论. 文章最后给出SAA问题的空间分解算法框架.

1SAA问题的收敛性分析

由二阶锥的定义,SSOCP问题可以被转化为

(3)

等价的,

并且

则式(3)可以转化为

(4)

令x为式(4)的可行点,定义如下的指标集

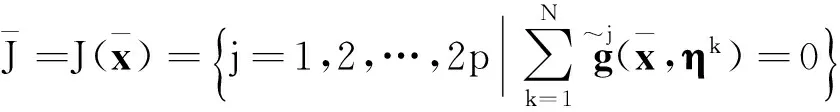
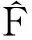
其中μ>0是罚参数. 具体的,

其中

因此,

并且

下面讨论随着N的增加,问题(4)收敛到问题(1). 特别的,将讨论当N→∞时,SAA问题(4)的解收敛到原问题的解. 首先,给出SAA方法的基本假设.

假设1

(2) 对于任意的s∈X以及足够小的t,矩母函数Ms(t)是有限的;

(3) 存在可测函数κ:Ω→R+,使得对所有的ξ∈Ω,s′,s∈X,有

(4) 对于足够小的t,κ(ξ)的矩母函数为Mk(t)=E[etk(ξ)],其中Ms(t)=E[et(g(s,ξ)-G(s))] 是随机变量g(s,ξ)-G(s)的矩母函数.

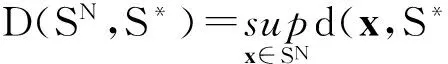
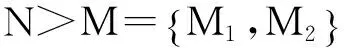
并且

令N>M,ε=ε1+με2,有

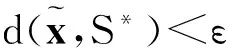
下面讨论随着样本容量的增加,SAA问题(2)的解以指数收敛率收敛到原问题(1)的解.

定理2令xN是SAA问题(4)的解集,S*是原问题(1)的解集.假设1成立,则对于任意的ε>0,存在正参数c(ε),d(ε)使得对于充分大的N,有

(5)

证明令ε>0,ε1>0,ε2>0,由定理1知,存在δ>0使得

故d(xN,S*)<ε. 因此由假设1,有

c(ε)e-Nd(ε).

2SAA问题的分解理论

首先介绍如下的定义和假设.

为VU-子空间,并且Rn=U⊕V,其中⊕表示空间的直和.

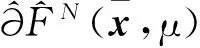
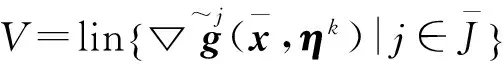
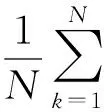
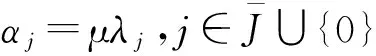
并且由U=V⊥知结论的第二部分成立.

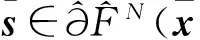
相应的,V-子空间上的最优解集为

(1) 关于变量u,v的非线性方程组

(6)

有唯一解v=v(u),并且v:RdimU→RdimV是二阶连续可微函数;

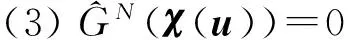
引理1关于αj的方程组

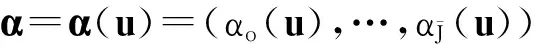
下面的定理给出U-拉格朗日函数的性质.

(1)Lu关于变量u是二阶连续可微函数;

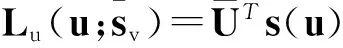
特别的,当u=0时,有,其中

其中

证明 (1) 由定理3结论(3),有

由于函数f和v(u)是二阶连续可微的,结论(1)成立.

(2) 根据链式法则,将下面的方程组关于变量u求导数,

即

其中

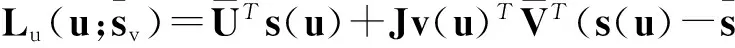
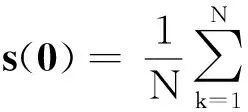
其中

根据文献[14]中的定理6.3的证明,有

因此

3算法和收敛性分析

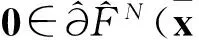
算法1(算法框架)

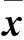
Step 1(停止准则)若

(7)

则停.

(8)

其中

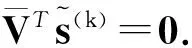
Step6(校正)置k=k+1,转Step1.

(9)

由式(8)知,

故

4结论

首先针对二阶锥规划问题,给出基于VU-空间分解的样本均值近似方法(SAA). 然后讨论了SAA子问题目标函数具有与VU-空间分解相关的原始对偶梯度结构. 进而,Rn空间可以分解为U和V两个直交的子空间. 目标函数在U-空间上是光滑的,具有与二阶展开相关的U-海赛阵. 因此,在设计求解SAA问题的算法上采用Newton方法以获得超线性的收敛速度.

参考文献:

[ 1 ]SHAPIROA,DENTCHEVAD,RUSZCZYNSKIA.Lecturesonstochasticprogramming:modelingandtheory[R].Philadelphia:SIAM, 2009.

[ 2 ]PAGNONCELLIBK,AHMEDS,SHAPIROA.Sampleaverageapproximationmethodforchanceconstrainedprogramming:theoryandapplication[J].JournalofOptimizationTheoryandApplications, 2009,142(2):399-416.

[ 3 ]FLIEGEJ,XUH.Stochasticmultiobjectiveoptimization:sampleaverageapproximationsandapplication[J].JournalofOptimizationTheory&Applications, 2011,151(1):135-162.

[ 4 ]WANGMZ,LINGH,GAOYL,etal.Sampleaverageapproximationmethodforaclassofstochasticvariationalinequalityproblems[J].JournalofSystemScienceandComplexity, 2011,24(6):1143-1153.

[ 5 ]LIUYC,XUHF,YEJJ.Penalizedsampleaverageapproximationmethodsforstochasticmathematicalprogramswithcomplementarityconstraints[J].MathematicsofOperationsResearch, 2010,36(36):670-694.

[ 6 ]SHUANGC,PANGLP,GUOFF,etal.StochasticmethodsbasedonNewtonmethodtothestochasticvariationalinequalityproblemwithconstraintconditions[J].MathematicalandComputerModeling, 2012,55(3):779-784.

[ 7 ]KANZOWC,FERENCZII,FUKUSHIMAM.Semismoothmethodsforlinearandnonlinearsecond-oderconeprograms[R].DepartmentofAppliedMathematicsandPhysics,KyotoUniversity, 2006.

[ 8 ]LIUYJ,ZHANGLWANDWANGYH.Convergencepropertiesofasmoothingmethodforlinearsecond-orderconeprogramming[J].AdvancesinMathematics, 2007,36(4):491-502.

[ 9 ]LIUYJ,ZHANGLW.ConvergenceofaugmentedLagrangianmethodfornonlinearoptimizationproblemsoversecond-ordercones[J].JournalofOptimizationTheoryandApplications, 2008,139(3):557-575.

[10]BAIYQ,WANGGQ.Primal-dualinterior-pointalgorithmsforsecond-orderconeoptimizationbasedonanewparametrickernelfunction[J].ActaMathematicaSinica(EnglishSeries), 2007,23(11):2027-2042.

[11]LEMARECHALC,OUSTRYF,SAGASTIZABALC.TheU-Lagrangianofaconvexfunction[J].TransactionsoftheAmericanMathematicalSociety, 2000,352(2):711-729.

[12]MIFFLINR,SAGASTIZABALC.VU-decompositionderivativesforconvexmax-functions[M]∥Ⅲ-posedVariationalProblemsandRegularizationTechniques.Berlin:SpringerBerlinHeidelberg, 1999:167-186.

[13]LEMARECHALC,SAGASTIZABALC.Morethanfirst-orderdevelopmentsofconvexfunctions:primal-dualrelations[J].JournalofConvexAnalysis, 1996,3(2):1-14.

[14]MIFFINR,SAGASTIZABALC.OnVU-theoryforfunctionswithprimal-dualgradientstructure[J].SIAMJournalonOptimization, 2000,11(2):547-571.

[15]MIFFINR,SAGASTIZABALC.Functionswithprimal-dualgradientstructureandU-Hessians[M]∥NonlinearOptimizationandRelatedTopics.NewYork:SpringerUS, 2000:219-233.

[16]MIFFINR,SAGASTIZABALC.Primal-dualgradientstructuredfunctions:second-orderresults;linkstoEpi-derivativesandpartlysmoothfunctions[J].SIAMJournalonOptimization, 2002,13 (4): 1174-1194.

[17]LANGS.Realandfunctionanalysis[M]. 3rded.NewYork:Springer-Verlag, 1993.

【责任编辑: 肖景魁】

A Fast Space Decomposition Method for Stochastic Second-Order Cone Programming Problem

LuYuan

(Normal School, Shenyang University, Shenyang 110044, China)

Abstract:Sample average approximation (SAA) method based on the space decomposition method to solve stochastic second-order cone programming problem is discussed. Under some moderate conditions, the SAA solution converges to its true counterpart with probability approaching one and convergence is exponential fast with the increase of sample size. Based on the decomposition theory, a superlinear convergent algorithm frame is designed to solve the SAA problem.

Key words:stochastic optimization; second-order cone programming; sample average approximation; space decomposition; superlinear convergent

文章编号:2095-5456(2016)03-0250-06

收稿日期:2016-01-06

基金项目:国家自然科学基金资助项目(11301347).

作者简介:陆媛(1981-),女,辽宁沈阳人,沈阳大学副教授,博士.

中图分类号:O 221

文献标志码:A