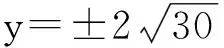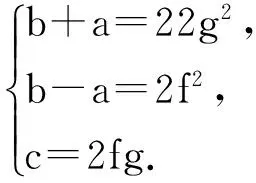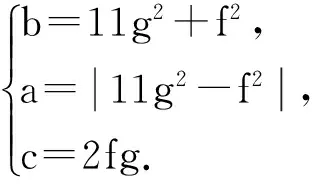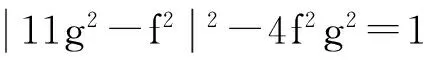一类孪生素数椭圆曲线整数点

官春梅, 席小忠

(1. 喀什大学 数学与统计学院, 新疆 喀什　844006; 2. 宜春学院 数学与计算机科学学院, 江西 宜春　336000)



一类孪生素数椭圆曲线整数点

官春梅1, 席小忠2

(1. 喀什大学 数学与统计学院, 新疆 喀什844006; 2. 宜春学院 数学与计算机科学学院, 江西 宜春336000)

摘要:运用初等的方法证明了孪生素数椭圆曲线E1:y2=x(x-11)(x-13)只有整数点(0,0),(11,0),(13,0)的结论.

关键词:孪生素数; 椭圆曲线; 整数点

不定方程整数解的讨论是数论研究中一项重要的内容,许多学者对这一内容都进行过研究,如文献[1-2]就讨论了两个不定方程的解.同样,确定椭圆曲线E1:y2=x(x-p)(x-q)与E2:y2=x(x+p)(x+q)在孪生素数p,q=p+2时的整数点的问题是一个有趣的数论问题,对其有着极其丰富的研究内容[3-8].文献[9]中,作者讨论了椭圆曲线E1:y2=x(x-3)(x-5)与E2:y2=x(x+3)(x+5)的整数点的问题.文献[10]中,作者讨论了椭圆曲线E1:y2=x(x-5)(x-7)与E2:y2=x(x+5)(x+7)的整数点的问题. 本文将探讨椭圆曲线E1:y2=x(x-p)(x-q)在孪生素数p=11,q=13时整数点的问题,并给出了相应的结论.

1主要结论及其证明

定理1孪生素数椭圆曲线方程E1:

(1)

只有整数点(0,0),(11,0),(13,0).

证明当y=0时,显然(0,0),(11,0),(13,0)是满足式(1)的3个整数点.下面讨论y≠0的情况. 设(x,y)是满足式(1)的1个整数点.由于y≠0,则y2>0,有013.

若0

下面讨论x>13的情况. 设d1=(x,x-11),d2=(x,x-13),d3=(x-11,x-13),则有

对d1,d2,d3的取值进行分类组合,可分为8种情况,对这8种情况分别讨论. 说明:以下所提到的a,b,c是两两互素的整数.

情形1(d1,d2,d3)=(1,1,1).

令x=a2,x-11=b2,x-13=c2,则y=±abc. 由此可得

2=(x-11)-(x-13)=a2-b2=(a+b)(a-b).

由上式可知,此时无整数解.

情形2(d1,d2,d3)=(11,1,1).

令x=11a2,x-11=11b2,x-13=c2,则y=±11abc. 由此可得x-(x-11)=11,即11a2-11b2=11. 进一步有(a+b)(a-b)=1.此时虽可得x=11,但-2=c2这在有理数集中是无解的,所以此时无整数点.

情形3(d1,d2,d3)=(1,13,1).

令x=13a2,x-11=b2,x-13=13c2,则y=±13abc. 由此可得

13=x-(x-13)=13a2-13c2,进一步有(a+c)(a-c)=1.此时虽可得x=13,但2=b2这在有理数集中是无解的,所以此时无整数点.

情形4(d1,d2,d3)=(1,1,2).

令x=a2,x-11=2b2,x-13=2c2,则y=±2abc. 由此可得2=(x-11)-(x-13)=2b2-2c2,进一步有(b+c)(b-c)=1.此时虽可得x=13,但13=x2这在有理数集中是无解的,所以此时无整数点.

情形5(d1,d2,d3)=(11,13,1).

令x=11×13a2,x-11=11b2,x-13=13c2,则y=±11×13abc. 由此可得13=x-(x-13)=11×13a2-13c2,进一步有11a2-c2=1.由于c≢0(mod11),则c2+1≡2,4,5,6,10(mod11),而此时11a2≡0(mod11),所以此时无整数点.

情形6(d1,d2,d3)=(1,13,2).

令x=13a2,x-11=2b2,x-13=26c2,则y=±26abc. 由此可得a2-2c2=1,b2-13c2=1.由x=13a2,x-11=2b2可得a≡1(mod2),再由a2-2c2=1,b2-13c2=1可得b≡1(mod2),c≡0(mod2),(b+a)(b-a)=11c2.那么,有

情形7(d1,d2,d3)=(11,1,2).

情形8(d1,d2,d3)=(11,13,2).

综合以上的讨论可得,式(1)只有整数点(0,0),(11,0),(13,0). 定理证毕.

2结语

对于椭圆曲线E1:y2=x(x-p)(x-q)与E2:y2=x(x+p)(x+q)在孪生素数p,q=p+2时的整数点的问题,本文就E1当p=11、q=13的情况进行了讨论,给出了此时所确定孪生素数椭圆曲线只有整数点(0,0),(11,0),(13,0)的结论.而对于其他的孪生素数p,q=p+2,E1与E2的整数点问题也是值得研究的问题.

参考文献:

[ 1 ] 杜先存,刘玉凤,管训贵. 关于丢番图方程x3±53=3py2[J]. 沈阳大学学报(自然科学版), 2014,26(1):81-83.

(DUXC,LIUYF,GUANXG.OnDiophantineequationx3±53=3py2[J].JournalofShenyangUniversity(NaturalScience), 2014,26(1):81-83.)

[ 2 ] 管训贵,杜先存. 关于丢番图方程x3+1=13py2的整数解[J]. 贵州师范大学学报(自然科学版), 2014,25(2):36-38.

(GUANXG,DUXC.OnIntegersolutionofDiophantineequationx3-1=13py2[J].JournalofGuizhouNormalUniversity:NaturalScience, 2014,25(2):36-38.)

[ 3 ]QIUDR,ZHANGXK.EllipticcurvesoftwinprimesoverGaussfieldandDiophantineequations[J]. 数学进展, 2000,29(3):279-281.

(QIUDR,ZHANGXK.EllipticcurvesoftwinprimesoverGaussfieldandDiophantineequationgs[J].AdvancesinMathematics, 2000,29(3):279-281.)

[ 4 ]QIUDR,ZHANGXK.Mordell-WeilgroupsandSelmergroupsoftwinprimeellipticcurves[J].ScienceinChina(MathematicsPhysicsAstronomy), 2002,45(11):1372-1380.

[ 5 ]LEMH.OnthesimultaneousPellequationx2-D1y2=dandz2-D2y2=d[J]. 数学进展, 2001,30(1):87-88.

(LEMH.OnthesimultaneousPellequationx2-D1y2=dandz2-D2y2=d[J].AdvancesinMathematics, 2001,30(1):87-88.)

[ 6 ]STROEKERRJ,TZANAKISN.ComputingallintegersolutionsofaGenus1equation[J].MathematicsofComputation, 2003,72(244):1917-1933.

[ 7 ] 陈历敏.Diophantine方程y2=px(x2+2)[J]. 数学学报, 2010,53(1):83-86.

(CHENLM.OntheDiophantineequationy2=px(x2+2)[J].ActaMathematicaSinica(ChineseSeries), 2010,53(1):83-86.)

[ 8 ] 崔保军. 椭圆曲线y2=px(x2+4)的正整数点[J]. 佳木斯大学学报(自然科学版), 2014,32(6):962-963.

(CUIBJ.OntheDiophantineequationy2=px(x2+4)[J].JournalofJiamusiUniversity(NaturalScienceEdition), 2014,32(6):962-963.)

[ 9 ]CHENHY.Integralpointsontwinprimesellipticcurvesforp=3[J]. 数学杂志, 2012,32(5):809-815.

(CHENHY.Integralpointsontwinprimesellipticcurvesforp=3[J].JournalofMathematics, 2012,32(5):809-815.)

[10] 陈候炎. 孪生素数椭圆曲线在p=5时的整数点[J]. 西南师范大学学报, 2011,36(1):34-38.

(CHENHY.Integralpointsontwinprimesellipticcurvesforp=5[J].JournalofSouthwestChinaNormalUniversity(NaturalScienceEdition), 2011,36(1):34-38.)

[11] 潘家宇. 关于丢番图方程x2-Dy4=1的一些注记[J]. 河南科学, 1997,15(1):18-22.

(PANJY.SomeremarksontheDiophantineequationx2-Dy4=1[J].HenanScience, 1997,15(1):18-22.)

【责任编辑: 肖景魁】

IntegralPointsofATwinPrimesEllipticCurve

Guan Chunmei1, Xi Xiaozhong2

(1.SchoolofMathematicsandStatistics,KashgarUniversity,Kashgar844006,China; 2.InstituteofMathematicsandComputerScience,YichunCollege,Yichun336000,China)

Abstract:Conclusion that twin primes elliptic curvey E1:y2=x(x-11)(x-13)has only three integral points(0,0),(11,0),(13,0)was proved by using elementary methods.

Key words:Twin primes; elliptic curve; integral points

文章编号:2095-5456(2016)03-0256-03

收稿日期:2015-01-21

基金项目:国家自然科学基金资助项目(11201411).

作者简介:官春梅(1976-),女,湖北竹山人,喀什大学讲师.

中图分类号:O 156

文献标志码:A