输入非均匀采样广义输出误差模型的递推贝叶斯参数辨识算法

景 绍 学

(淮安信息职业技术学院电气工程系　江苏 淮安 223003)(江苏大学电气信息工程学院　江苏 镇江 212013)



输入非均匀采样广义输出误差模型的递推贝叶斯参数辨识算法

景 绍 学

(淮安信息职业技术学院电气工程系江苏 淮安 223003)(江苏大学电气信息工程学院江苏 镇江 212013)

摘要针对传统最小二乘算法在辨识过程中没有考虑噪声的协方差和参数的先验概率密度的问题，提出一种递推贝叶斯算法。该算法以最大化参数的后验概率密度函数为准则进行参数估计。实验结果证明所提算法可以获得更高精度的参数估计值。收敛性分析表明，该算法给出的参数估计值收敛于参数真值。该算法综合考虑了噪声方差、数据的先验概率分布和参数的先验概率分布，可以获得比最小二乘法更高的精度的估计值。

关键词输入非均匀采样系统广义输出误差模型递推贝叶斯算法参数估计

0引言

在工业生产中存在着这样一类系统，它们的输入采样和(或)输出刷新呈现出不等时间间隔的非均匀的特点，这类系统被称为非均匀采样系统[1,2]。这类系统有的是由于硬件设备的限制、经济条件的制约或环境因素的影响等原因造成的被动非均匀采样系统,如产品组分和浓度的检测[3,4]、熔融指数的人工采样[5,6]和Kappa值的测量[7,8]等。还有的是为了在同样采样点数的情况下获得更多的有用信号而根据信号幅值变化情况主动调整采样间隔的主动非均匀采样系统[9]。近年来，非均匀采样系统的研究受到了国内外专家和学者的普遍关注，特别是作为状态估计和控制理论基础的系统辨识领域[10-18]。

在白噪声的前提下，传统算法，如最小二乘算法等，都能给出非均匀采样系统的参数无偏估计。而在工业实践中的扰动都是有色噪声，传统的最小二乘等算法不能满足无偏估计的要求[19]。为了获得参数的无偏估计，研究人员提出了一系列的算法。例如，基于滤波的算法[20]、最大似然算法[21,22]、基于辅助模型的算法[23]等。基于滤波的算法首先采样一个动态的滤波器来白化有色噪声，然后使用传统算法，如最小二乘算法等，获得无偏估计。但是当工业过程输出信号噪信比较大或者参数较多时这类算法会出现估计偏差[24]。并且最大似然类算法给出的估计值都是渐近无偏的，也就是说最大似然算法并不能保证给出的所有估计都是无偏的。此外，最大似然算法的计算量比较大，也在一定程度上限制了其应用[24]。基于辅助模型的算法，如基于辅助模型的递推最小二乘算法(AM-RLS)和基于辅助模型的随机梯度(AM-SG)等，可以同时对系统模型和噪声模型的无偏估计，是一类比较有应用前景的算法。但在辨识过程中，AM-RLS和AM-SG都没有把系统噪声的方差考虑进辨识算法以提高算法的辨识精度，所以本文的基本思路是考虑结合噪声的方差，基于辅助模型的思想和递推最小二乘的形式提出一种递推贝叶斯RB(recursiveBayesian)辨识算法。并用输入非均匀采样广义输出误差模型NUSIDGOE(non-uniformlysampledinputdataforgeneralizedoutputerrormodel)验证了算法的有效性。

1问题描述

考虑如图1所示的输入非均匀更新和输出定期采样的NUSIDGOE模型。图中，包括零阶保持器Hτ、线性时不变过程Pc和采样器ST三个部分。其中，u(t)和x(t)分别是输入信号和无噪输出信号；y(t)为有噪输出；w(t)是有色噪声；y(kT+T)是采样时刻t=kT+T时刻的输出采样值，其中T为输出采样周期，也称框架周期。

图1　输入非均匀采样广义输出误差模型框图

假定输入非均匀采样时间间隔为{τ1,τ2,…,τr}，它们满足如下的条件：T=τ1+τ2+…+τr。定义t0=0,ti=ti-1+τi，其中i=1,2,…,r，那么输入u(t)可以写为：

(1)

其中k=0,1,2,…。

如图1所示，若Pc和w(t)采用文献[20]的形式，则NUSIDGOE模型的连续输出y(t)可以表示为：

y(t)=x(t)+w(t)

(2)

其中：

(3)

(4)

A(z-1) = 1 +a1z-1+a2z-2+ … +anaz-na,B1(z-1) =b10+b11z-1+b12z-2+ … +b1n bz-nb,Bi(z-1) =bi1z-1+bi2z-2+ … +bin bz-nb

(5)

C(z-1)=1+c1z-1+c2z-2+…+cncz-nc,D(z-1)=1+d1z-1+d2z-2+…+dndz-nd

(6)

定义参数向量如下：

(7)

其中：

θs=[a1,…,ana,b10,…,b1nb,b21,…,b2nb,…,br1,…,brnb]T∈ns

(8)

θn=[c1,c2,…,cnc,d1,d2,…,dnd]T∈nn

(9)

ns=na+rnb+1，nn=nc+nd，n=ns+nn;下标s和n分别表示过程模型和噪声模型。

类似地，分别定义信息向量φ如下：

(10)

φs(k)= [-x(kT-T),…,-x(kT-naT),u(kT),…,

u(kT-nbT),u(kT-T+t1),…,u(kT-nbT+t1),

…,u(kT-T+tr-1),…,u(kT-nbT+tr-1)]T∈ns

(11)

φn(k)=[-w(kT-T),-w(kT-2T),…,-w(kT-ncT),

v(kT-T),v(kT-2T),…,v(kT-ndT)]T∈nn

(12)

对于t=kT时刻，等式可以改写成：

y(k)=x(k)+w(k)=φT(k)θ(k)+v(k)

(13)

其中：

(14)

(15)

假定系统的模型结构是已知的，即(na,nb,nc,nd)和输入采样次数r均是已知的，那么算法的目的就是如何利用观测数据D(k)估计参数向量θ。

2递推贝叶斯参数辨识算法

贝叶斯方法的主要观点就是把待估计参数作为一个随机变量，通过观测与该变量相关的其他随机变量来推测该变量的值[25]。在提出的算法中，以最大化后验概率密度作为估计准则，即：

(16)

根据贝叶斯公式，参数的后验概率密度函数表示为：

(17)

其中p(y(k)|θ,D(k-1))为在给定参数θ和数据条件下输出y(k)的先验概率密度。

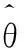
(18)

(19)

于是参数的后验密度函数p(θ|Dk)的表达式为：

(20)

(21)

其中：

(22)

(23)

这样就得到了递推贝叶斯(RB)算法的简洁形式：式(22)和式(23)。为了避免计算P(k)的逆矩阵以减小算法的计算量，对式(23)运用矩阵求逆反演公式，得到：

(24)

(25)

(26)

P(k)=[I-L(k)φT(k)]P(k-1)

(27)

(28)

其中：

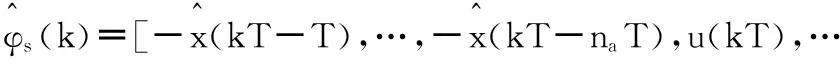
u(kT-nbT),u(kT-T+t1),…,u(kT-nbT+t1),

…,u(kT-T+tr-1),…,u(kT-nbT+tr-1)]T∈ns

(29)

(30)

(31)

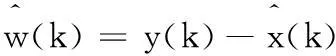
(32)

(33)

噪声方差可以用下式进行估计：

(34)

于是，RB算法可以整理如下：

(35)

(36)

(37)

RB算法的计算步骤如下：

Step1收集输入输出数据u(kT+ti)和y(k)，i=0,1,2,…,r，k=1,2,…。

P(0)=p0In,θ(0)=1n/p0,p0=106

其中1n为元素全为1的n维列向量。

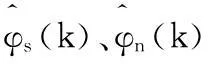
Step8令k=k+1，转step4。

3收敛性分析

定理1对于系统式(13)和RB算法式(22)、式(23)，假设{v(t),Ft}是定义在概率空间{Ω,F,P}上的鞅差向量序列，其中{Ft}是截至时刻t之前所有观测数据生成的σ代数序列[26]；如果噪声序列{v(t)}满足如下假设：

(38)

并且存在正常数c1,c2和t0使得下面的持续激励条件成立[27]：

(39)

那么算法给出的参数估计值收敛于真值，即：

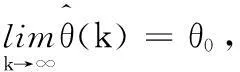
(40)

其中θ0为参数真值。

证明在式两边同时减去θ0并用φT(k)θ0+v(k)代替y(k)，得到：

(41)

其中：

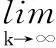
在式(23)两边同乘以P(k)，则Q(k)可以写成：

(42)

令λ为矩阵Q(k)的一个特征值，p为其对应的特征向量，那么下式成立：

Q(k)p=λp

(43)

考虑到式(42)、式(43)可以写成：

P(k)P-1(k-1)p=λp

(44)

在式(44)的两边同乘以P-1(k)，考虑到式(23)，并整理得：

(45)

在式(45)两边同乘以pT并整理得：

(46)

4仿真实例

考虑如下的NUSIDGOE模型：

其中：

A(z)=1-1.4780z-1+0.9324z-2

B1(z)=0.1519+0.04206z-1

B2(z)=0.0779+0.1824z-1

C(z)=1-0.6z-1

D(z)=1+0.33z-1

r=2,τ1=2s,τ2=5s,t1=τ1=2s,t2=τ1+τ2=7s

表1　RB算法参数估计值和估计误差随数据长度k变化情况

表2　AM-RGELS算法参数估计值和估计误差随数据长度k变化情况

图2　RB和AM-RGELS算法参数估计误差随数据长度变化情况图

根据表1、表2的数据和图2的仿真结果可以看出：

(1) 数据长度增加时，两种算法的估计误差都在变小；

(2) 对同样的数据长度，RB算法比AM-RGELS算法的估计精度高；

(3) 在相同噪声水平下，RB算法比AM-RGELS算法的收敛速度要快。

5结语

本文针对输入非均匀采样广义输出误差模型提出了一种递推贝叶斯参数估计算法。它以通过最大化参数的条件后验概率密度函数作为估计准则，由于不仅考虑了参数的先验概率密度而且还考虑了数据的先验概率密度。因此该算法与单纯考虑数据的概率密度的极大似然类参数估计方法相比，精度更高。同时，该算法的辨识精度也会比传统最小二乘算法略高，因为它在辨识过程中考虑了噪声的方差。综上所述，该算法把给定数据集下最可能出现的参数值作为参数的估计值。收敛性分析表明，所提算法的参数估计值能收敛到真值，仿真结果表明了算法的有效性和较高的估计精度。

参考文献

[1]AlbertosP,CrespoA.Real-timecontrolofnon-uniformlysampledsystems[J].ControlEngineeringPractice,1999,7(4):445-458.

[2]CuencaA,SaltJ.RSTcontrollerdesignforanon-uniformmulti-ratecontrolsystem[J].JournalofProcessControl,2012,22(10):1865-1877.

[3]LiW,HanZ,ShanSL.SubspaceidentificationforFDIinsystemswithnon-uniformlysampledmultiratedata[J].Automatica,2006,42(4):619-627.

[4]DingF,LiuG,LiuXP.Partiallycoupledstochasticgradientidentificationmethodsfornon-uniformlysampledsystems[J].IEEETransactionsonAutomaticControl,2010,55(8):1976-1981.

[5]FortunaL,GrazianiS,XibilliaM.Softsensorsforproductqualitymonitoringindebutanizerdistillationcolumns[J].ControlEngineeringPractice,2005,13(4):499-508.

[6]GjerkesH,MalensekJ,SitarA,etal.Productidentificationinindustrialbatchfermentationusingavariableforgettingfactor[J].ControlEngineeringPractice,2011,19(10):1208-1215.

[7]OgawaM,OhshimaM,MorinagaK,etal.Dualityinferentialcontrolofanindustrialhighdensitypolyethyleneprocess[J].JournalofProcessControl,1999,9(1):51-59.

[8]SharminR,SundararajU,ShanS,etal.Inferentialsensorsforestimationofpolymerqualityparameters:IndustrialapplicationofaPLS-basedsoftsensorforaLDPEplant[J].ChemicalEngineeringScience,2006,61(19):6372-6384.

[9] 汪安民.基于非均匀采样的信号频率检测方法及其实现[D].武汉:华中科技大学,2004.

[10] 丁锋,陈通文,萧德云.非均匀周期采样多率系统的一种辨识方法[J].电子学报,2004,32(9):1414-1420.

[11]MizumotoI,ChenT,OhdairaS,etal.AdaptiveoutputfeedbackcontrolofgeneralMIMOsystemsusingmultiratesamplinganditsapplicationtoacart-cranesystem[J].Automatica,2007,43(12):2077-2085.

[12]ChenF,GilsonM,AgueroJC,etal.Closed-loopidentificationofcontinuous-timesystemsfromnon-uniformlysampleddata[C]//ControlConference(ECC),2014European.Strasbourg:IEEE,2014.

[13]JohanssonR,CesconM,StahlF.Continuous-timemodelidentificationusingnon-uniformlysampleddata[C]//AFRICON,2013.Mauritius:IEEE,2013.

[14]DingJ,LinJ.Modifiedsubspaceidentificationforperiodicallynon-uniformlysampledsystemsbyusingtheliftingtechnique[J].Circuits,Systems,andSignalProcessing,2014,33(5):1439-1449.

[15]WangH,LiuT.Recursivestate-spacemodelidentificationofnon-uniformlysampledsystemsusingsingularvaluedecomposition[J].ChineseJournalofChemicalEngineering,2014,89(1):1-6.

[16]DingF.Hierarchicalmulti-innovationstochasticgradientalgorithmforHammersteinnonlinearsystemmodeling[J].AppliedMathematicalModelling,2013,37(4):1694-1704.

[17]ChenF,GarnierH,GilsonM.RefinedInstrumentalVariableIdentificationofContinuous-timeOEandBJModelsfromIrregularlySampledData[C]//11thIFACInternationalWorkshoponAdaptationandLearninginControlandSignalProcessing.Caen:IFAC,2013.

[18]DingF,ChenT.Hierarchicalidentificationofliftedstate-spacemodelsforgeneraldual-ratesystems[J].IEEETransactionsonCircuitsandSystemsI:fundamentaltheoryandapplications.2005,52(6):1179-1187.

[19] 崔桂梅,关英辉,张勇.一类有色噪声干扰系统的有辨识研究[J].科学技术与工程,2010,10(18):4358-4362.

[20]XieL,YangHZ,DingF.Recursiveleastsquaresparameterestimationfornon-uniformlysampledsystemsbasedonthedatafiltering[J].MathematicalandComputerModeling,2011,54(1):315-324.

[21]LiJH,DingF.MaximumlikelihoodstochasticgradientestimationforHammersteinsystemswithcolorednoisebasedonthekeytermseparationtechnique[J].Computers&MathematicswithApplications,2011,62(11):4170-4177.

[22]LiJH,DingF,YangGW.Maximumlikelihoodleastsquaresidentificationmethodforinputnonlinearfiniteimpulseresponsemovingaveragesystems[J].MathematicalandComputerModeling,2012,55(3-4):442-450.

[23] 丁锋.系统辨识(4):辅助模型辨识思想与方法[J].南京信息工程大学学报:自然科学版,2011,3(4):289-318.

[24] 方崇智,萧德云.过程辨识[M].北京:清华大学出版社,1988.

[25]PeterkaV.BayesianApproachtoSystemIdentification:TrendsandProgressinSystemIdentification[M].NewYork:PergamonPress,1981.

[26]GoodwinG,SinK.AdaptiveFilteringPredictionandControl[M].NewYork:Prentice-Hall,1984.

[27]DingF,ChenHB,LiM.Multi-innovationleastsquaresidentificationmethodsbasedontheauxiliarymodelforMISOsystems[J].InternationalJournalofAppliedMathematicsandComputerScience,2007,187(2):658-668.

RECURSIVE BAYESIAN PARAMETER IDENTIFICATION ALGORITHM FOR GENERALOUTPUTERRORMODELSWITHNON-UNIFORMLYSAMPLEDINPUTDADA

Jing Shaoxue

(Department of Electrical Engineering,Huaian College of Information and Technology,Huaian 223003,Jiangsu,China)(School of Electrical and Information Engineering,Jiangsu University,Zhenjiang 212013,Jiangsu,China)

AbstractIn light of that traditional least squares method does not take into account the covariance of noise and the priori probability density of parameters in the process of identification, we proposed a recursive Bayesian parameter identification algorithm. The algorithm uses the posterior probability density function of maximised parameters as the criterion to estimate parameters. Experimental result proved that the proposed algorithm could acquire the estimates of parameters in higher accuracy. Convergence analysis indicated that the estimates of parameters provide by the proposed algorithm converged to their true values. The algorithm comprehensively considers the noise variance and the priori probability distributions of data and parameters, it is able to obtain the estimates with higher accuracy than the least-squares.

KeywordsNon-uniformly sampled input data systemsGeneral output error modelRecursive Bayesian algorithmParameter estimation

收稿日期：2014-12-08。江苏省研究生培养创新工程项目(CXLX12_0648)。景绍学，讲师，主研领域：过程控制，系统辨识。

中图分类号TP273

文献标识码A

DOI:10.3969/j.issn.1000-386x.2016.06.078