直接精简密集点云的三角网格重建

董天琪　张志毅

(西北农林科技大学信息工程学院　陕西 杨凌 712100)



直接精简密集点云的三角网格重建

董天琪张志毅*

(西北农林科技大学信息工程学院陕西 杨凌 712100)

摘要为解决快速传输需求，从稠密点云直接生成精简的三角网格模型，提出一种自适应立体栅格划分方法，并给出以立体栅格为基本单元的三角网格重建过程。首先以各点无差异的宏观估测方法获得立体栅格的边长，将点云数据分割为栅格单元。然后选取基本单元中数据点为种子点，设定三角形边长以近似正6邻域为约束，构建初始三角网格，再逐层外扩完成三角网格重建。该方法的优点在于可将简化和重建过程融为一体。实验结果表明所提方法速度较快，鲁棒性较好。

关键词精简密集点云网格重建外扩

0引言

点云数据是对现实世界物体形状最自然的表示方法之一，但是它不能表示物体的拓扑信息。近些年来已经有多种成熟的测量设备能够高速获取现实场景的三维点云数据。表面重建是从点云重构出忠实于原始曲面的三角形网格过程。其在逆向工程、数据可视化、机器视觉、虚拟现实、医疗技术等领域中都具有广泛的应用。文献[1]回顾了国内外的研究现状及商业软件开发情况，对目前逆向工程研究与应用存在的问题及解决的对策提出了讨论。目前也出现了文献[2]这种针对性较强的研究成果。散乱点云曲面重建的关键在于拓扑结构的正确建立，而由于数据信息的不完整性，这也成为曲面重建的难点所在。根据现有算法的特点，可以将它们分为以下几类：隐式曲面算法、参数曲面算法、基于学习的方法、Delaunay三角剖分算法等。隐曲面方法[3]重建效果良好，但模型较难选定。Delaunay方法研究成果众多，文献[4,5]中的Crust方法最为广泛。Cocone方法[6]也是备受关注的方法之一。Crust方法较为复杂，而Cocone方法则需要针对不同点云数据进行相应的方法的变化。对于大规模的数据来讲，Delaunay方法重建速度慢。文献[7]提出一种基于Delaunay三角化区域增长式的曲面重建方法。较以往方法具有人为参与更少、适用范围更广的优点，但算法效率有待提高。外扩方法容易理解和实现，但将三角形添加进已三角化的区域是其难点。其他方法[8-10]有的通过Voronoi图，有的利用平面投影线加快建模速度，有的基于多视图的三维模型进行重建。

随着激光扫描设备的发展，包含被测物体更多细节的大量数据的获取成为可能。针对高密度点云数据，文献[11]中提出首先采用基于密度聚类的方法筛选三维点云，然后进行网格重建。浙江大学的蔺宏伟等人[12]提出了根据点云内在属性进行重建的方法。文献[13]提出了对数据进行栅格化的方法，但没有给出一个合适的栅格规则。文献[14]采用自适应八叉树分割点云的方法进行表面模型重建，提高了模型重建的效率，也能够体现点云模型的细节特征，但与传统的三角网生长法相比，有一定的冗余网格。本文提出一种自适应立体栅格划分方法，并给出以立体栅格为基本单元实现三角网格重建的实现过程，解决了快速传输需求。对于高密度的点云精简重建速度快，并且具有可将简化和重建过程融为一体的优点。

1概念

已知集合P，对于其中的任一点p，定义该点的r邻域点为点集P中到p点距离不大于r的点集合，即：

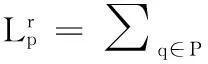
定义该点的环域点为点集P中到p点距离介于r+σ与r-σ之间的点的集合，即：

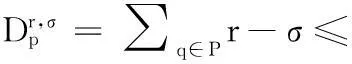
2算法描述

2.1获得长方体包围盒

要实现对点云的分割，首先要获得散乱点云的长方体包围盒。遍历全部点云，找到x，y，z三个坐标轴方向上最小和最大的共六个点，分别只取它们在对应坐标轴上的分量，组成两个点，记为两个点Pmax，Pmin，这两个点即长方体包围盒最长对角线的两个端点。

2.2划分立方体栅格及立方体边长选择策略

长方体包围盒的长、宽、高，分别除以立方体的边长，向上取整，即得点云分别在x，y，z坐标方向上立方体的个数，记为CubeNum(x,y,z)。立方体的编号通过它在x、y、z坐标方向上的编号组成的一个向量Id(x,y,z)来表示，获取邻域环域时需要检索立方体的编号，为检索方便，需将此立方体编号转化为整数，方法如下：

L=Idx×CubeNumy×CubeNumz+Idy×CubeNumz+Idz

检索邻域和环域受影响的立方体时，实际上使用的是数字L。

在划分立方体栅格的过程中，立方体的边长的选择尤为重要，它的大小直接影响到模型的重建效果。其具体的选择策略描述如下。

由于扫描得到的是表面点，而立方体是根据长方体包围盒来划分的，所以在物体的内部会有很多空的立方体。因此不能用体积来计算，本文选择使用表面积进行计算。实际上是利用了长方体包围盒的表面积近似等于所要重建的模型的表面积。

通过计算可以得出长方体包围盒的长、宽、高即Pmax-Pmin所得的x、y、z分量，分别记为Px、Py、Pz，长方体包围盒的表面积近似表示为物体的表面积，即：

(PxPy+PxPz+PyPz)×2

记为S。另外，点云中点的个数即总点数记为N。为便于后期对生成的网格进行曲面拟合，每个非空立方体内至少要有多个数据点存在，一般为满足三次曲面拟合，至少应有16个点，具体所取数值记为n，N除以n即可以得出需要立方体的个数。立方体边长记为a，综上所述，得出：

即：

(1)

划分的立方体，以编号命名文件保存立方体中的点，并非所有连续编号的立方体都有其对应的文件，没有点的立方体不会生成文件，所以效率上并没有多余的浪费。

2.3重建过程

2.3.1初次外扩方法

重建的第一步是获取种子点。由于是扩展重建，所以适宜从点云的中心开始，本文所有实验均选取距离长方体包围盒中心最近的点。根据2.1节中得到的Pmax，Pmin计算长方体包围盒的中心，遍历所有点得到距离中心最近的点设为初始种子点。

得到种子点后，要根据种子点进行外扩。对于一次外扩，它的准备工作有以下几项。

• 第二，根据邻域点集计算该邻域的微切平面，得到微切平面的法向量。目的是为后续排序工作确定z轴正向。

• 第三，对环域点集进行排序。排序需要一个值作为排序的标记点。已知种子点O，如果当前生成的三角形是第一个三角形，则当前三角形的第二个顶点可在环域中随机选取，如果当前生成的三角形不是第一个三角形，则由于队列的搜索顺序并不可随机选取。具体的排序方法为：标记点记为A，OA作为微切平面上的x轴正向，z轴正向为微切平面的法向量与O点之差，由此既确定搜索的时针时序，本文采用逆时针搜索。计算环域点与O点连线与OA夹角的cos值，并计算叉乘结果与z轴正向比较，即知该点与OA的逆时序夹角是否超过180°，如果超过则取负值并减去2，使得cos函数在0～2π上是变成一个连续的递减函数，由此可以根据它对环域点进行排序。

准备工作做好后，接下来就是三角形生成的过程。具体策略如下。

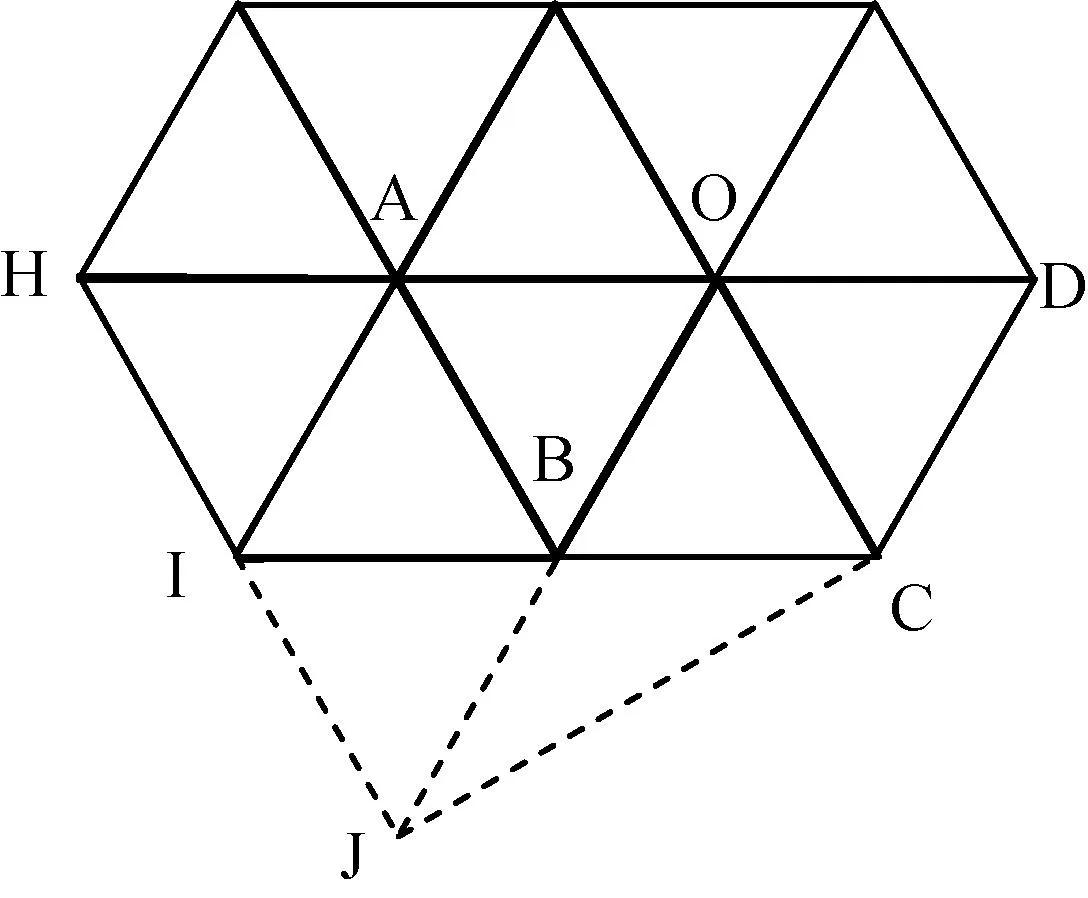
图1　找到合适点组成三角形状况图

依次检查排序后环域中的点与A点的距离，找到距A点最接近L的点。对于大部分数据来说，不需要搜索整个环域，只需所求点满足一定条件即认为已找到。本文设置找到点距A大于0.6L即标记为已找到，0.6L为下限，保证等腰三角形的底角以70°至75°为上限而非过于苛刻得要求正三角形。由于搜索的环域已经排序，当搜索到距1.4L(1.4L为上限，即保证等腰三角形的底角以45°为下限。)的位置，会判断是否已经找到合适的点。如果没有找到，则进行分类讨论：若当前点已满足与队头的位置关系，则直接处理；若不合适则将当前点而非点A作为新三角形的第一个点，继续向下搜索。如果找到则跳出循环判断该点与队头的位置关系。判断点与队头位置关系的策略如下。

找到合适点的情形如图1所示，点J为找到的合适点。

图1中，B为当前种子点，队列顺序为CDEFGHI。判断J与队头C的关系并做相应处理。本文将其分为以下三种情况：

a.如果JC较大，本文设为大于2L。说明扇形BJC可以容纳不止一个三角形，则先生成△BIJ，返回搜索。

b.如果JC非常小，本文设置为小于0.4L，此时本文认为IC接近于1.4L，满足上文中以45°为等腰三角形底角下限的要求。继而认为IC≈IJ≈L(由于模型是立体的，图1显示为平面效果，所以实际上IC不一定通过B，尤其在JC非常小的前提下)，则生成三角形△BIC。种子点变为C。

c.如果JC中等大小，本文设置为0.5L至2L，即至少可容纳两个底角最大即70°～75°的等腰三角形，至多容纳两个底角最小即45°的等腰三角形，满足上文的条件，此时直接生成两个三角形，△BIJ和△BJC。种子点变为C。

2.3.2外扩整体过程及方法

外扩是一个队列遍历种子点不断生成三角形，不断有新种子点入队、旧种子点出队的过程。本文中搜索顺序是从队尾搜索到队头，直到队列中没有点。由于始终采取逆时针遍历，每当数据点出队即作为当前种子时，除第一次扩展需特殊处理外(只需设置标记位即可解决此问题)，当前种子的搜索区域始终是队尾—当前种子点—队伍这样一个扇形区域，如图2-图3所示。

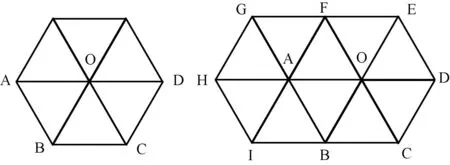
图2　左侧为第一次扩展图，右侧为第二次扩展图

图3　第三次扩展图

图2左侧为第一次扩展图，种子点为O，此时队列中点的顺序为ABCDEF，右侧为进一步进行扩展图，种子点为A，队列中点的顺序为BCDEFGHI，此时以A为种子点时的搜索区域正是左侧图对应种子序列从队头到队尾的扇形区域。

但是这样并不能保证所有的点都被遍历，需要在外侧再设置循环，判断是否所有的点标记为已读。最终得到三角网格。

3实验与分析

本文算法采用C语言实现，并在主频为2.60GHz，内存2GB的PC机上进行测试。本文分别对标准试验数据斯坦福兔子和实验室扫描的实测数据进行了测试。

斯坦福兔子数据包含数据点20 002个，根据本文介绍的划分立方体方法计算得到(以下数值均为取整后数值)，Pmax=(511,441,508)，Pmin=(200,200,200)，Px、Py、Pz分别为311、241、308，继而表面积S=489 934，根据前文所述，n取16，则由式(1)计算得a约为19.7，取整为20。式(1)中S和N都为确定值，所以，有且仅有n的取值影响a。n的取值为满足三次曲面拟合所取数值。为测试实验结果，本文将n取4、8又可得到a=10、a=14两个值。即最终本文分别取小立方体边长a为10、14、20进行实验，得到结果比对如图4和表1所示。图4展示了立方体边长分别取不同数值的效果及原始数据效果。表1列出了重建的详细信息。

图4　左上为立方体边长为10的结果，右上为立方体边长为14的结果，左下为立方体边长为20的结果，右下为原始高密度点云的效果

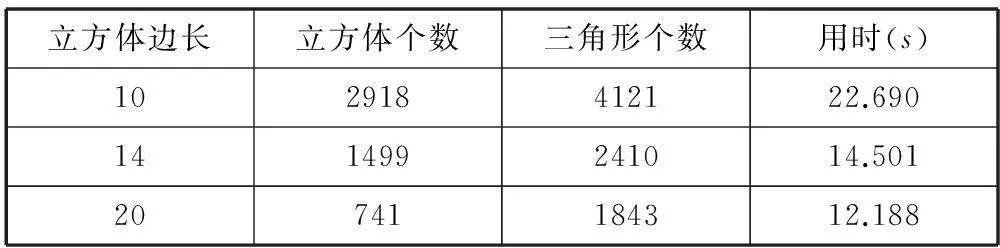
立方体边长立方体个数三角形个数用时(s)102918412122.690141499241014.50120741184312.188

由表1可知，本文对于密集散乱点云的网格数据精简重建速度快，且根据欧拉公式可算出对应于立方体边长选10、14、20时的简化率分别为89.686%，93.966%，95.380%的前提下，本文所提出的方法均能保持基本形状，有良好的鲁棒性。

文献[15]是一种基于顶点重要度的保形网格简化方法，其数据显示，当顶点数为4850时，简化率达到91.81%时所用时间为8.24s，且简化率越高，耗时越长。推算该方法当顶点数大于20 000时，达到同样简化率所用时间约为33.979s，而本文方法处理大于20 000点以上数据时(如上文斯坦福兔子数据)，达到精简率93.966%仅需14.501s，达到精简率95.380%仅需12.188s，可见本文精简速度较快。并且本文方法在立方体边长取值较大时，精简率越高，重建时间越短，将简化和重建过程融为一体。

本文还对实验室扫描的实测数据进行了测试。虽然自扫描数据存在噪声大，存在大量重复点等缺点，但本文方法仍取得了良好的实验结果。第一个实验数据是一个古玩瓶子模型，单面扫描有18 553个点，根据本文介绍的划分立方体方法计算得到(以下数值均为取整后数值)，Pmax=(214,136,234)，Pmin= (51,38,11)，Px、Py、Pz分别为163、98、223，继而表面积S=148 354，由于该扫描数据为单侧面，所以表面积本文取一半即S=74 177，n取16，则由式(1)计算得a约为7。立方体边长7.0，运行时间9.879s。效果如图5所示。

图5　瓶子模型网格重建效果。左上为本文实验效果，右上为扫描得到的密集数据。下侧为古玩瓶实物图

第二个数据是本实验室自扫描兵马俑模型，侧面数据点96 780个，根据本文介绍的划分立方体方法计算得到(以下数值均为取整后数值)，Pmax=(424,76,711)，Pmin= (-129,-135,394)，Px、Py、Pz分别为553、211、317，继而表面积S=717 742，由于该扫描数据为单侧面，所以表面积本文取一半即S=358 871，n取16，则由式(1)计算得a约为8。边长取8，运行时间30.595s。效果如图6所示。

图6　兵马俑模型网格重建效果

由于实测扫描数据噪声较大，所以实验结果边缘略显琐碎，但仍能保持基本形状，取得了较为良好的效果。

4结语

本文提出一种自适应立体栅格划分方法，并给出以立体栅格为基本单元实现三角网格重建的实现过程。首先将点云数据分割为栅格单元，然后通过选取基本单元中数据点为种子点和设定三角形边长以近似正6邻域为约束来构建初始三角网格，再逐层外扩完成三角网格重建。本文方法解决了快速传输需求，从高密度点云直接生成精简的三角网格模型，从实验结果来看，对于高密度的点云精简重建速度快，鲁棒性较好，并且具有可将简化和重建过程融为一体的优点。

参考文献

[1] 陈建良,童水光.逆向工程技术研究进展[J].中国机械工程,2002,13(16):1430-1436.

[2] 崔汉国,胡怀宇,张涛,等.空间自由管道点云重建方法[J].海军工程大学学报,2011,23(2):76-79.

[3]HoppeH,DeRoseT,DuchampT,etal.SurfaceReconstructionfromUnorganizedPoints[J].ACMSIGGRAPHComputGraphics,1992,26(2):71-78.

[4]AmentaN,BernM,KamvysselisM.ANewVoronoi-basedSurfaceReconstructionAlgorithm[C]//Proceedingsofthe25thAnnualConferenceonComputerGraphicsandInteractiveTechniques,1998:415-421.

[5]AmentaN,ChoiS,KolluriRK.ThePowercrust[C]//Proceedingsofthe6thACMSymposiumonSolidModelingandApplications,2001:249-260.

[6]DeyTK,GiesenJ,HudsonJ.DelaunayBasedShapeReconstructionfromLargeData[C]//ProceedingoftheIEEESymposiumonParallelandLarge-DataVisualizationandGraphic,2001:19-27.

[7] 袁方,唐杰,武港山.一种基于三维Delaunay三角化的曲面重建算法[J].计算机技术与发展,2011,21(10):14-18.

[8] 纪志浩,于明旭.基于点云数据三维重建方法的研究[J].黑龙江工程学院学报:自然科学版,2014,28(3):7-9.

[9] 陈治睿,官云兰,杨鹏,等.基于点云数据的建筑物快速三维重建方法[J].江西科学,2011,29(5):603-606.

[10] 段春梅.基于多视图的三维模型重建方法研究[D].山东:山东大学,2009.

[11] 陈晓霞,陈孝威.三维重建中散乱点云的聚类筛选与网格重建[J].计算机系统应用,2011,20(4):141-144.

[12]HongweiLin,ChiewlanTai,GuojinWang.AMeshReconstructionAlgorithmDrivenbyanIntrinsicPropertyofaPointCloud[J].Computer-AidedDesign,2004,36(1):1-9.

[13] 聂建辉,马孜,胡英,等.针对密集点云的快速曲面重建算法[J].计算机辅助设计与计算机图形学学报,2012,24(5):574-582.

[14] 杨客,张志毅,董艳.基于自适应八叉树分割点云的表面模型重建[J].计算机应用与软件,2013,30(6):83-87.

[15] 董艳,张志毅,杨客.基于顶点重要度的保形网格简化方法研究[J].计算机工程与设计,2013,34(5):1889-1895.

TRIANGULAR MESH RECONSTRUCTION BY DIRECTLY SIMPLIFYINGDENSEPOINTCLOUD

Dong TianqiZhang Zhiyi*

(College of Information Engineering,Northwest A&F University,Yangling 712100,Shaanxi,China)

AbstractTo address the needs of rapid transmission and to generate the streamlined triangular mesh model directly from dense point cloud, this paper presents an adaptive method for three-dimensional grid division, and gives the reconstruction process of triangular mesh which uses the three-dimensional grid as basic unit. First, by using the macro-estimation method of no difference between points the method obtains the side length of three-dimensional grid, and segments the point cloud data into grid units. Then it selects the data points in basic unit as the seed points, and sets the triangle side lengths to be constrained with approximate positive 6 neighbourhoods to build the initial triangle mesh, and then expands outwardly layer by layer to complete the triangular mesh reconstruction. The advantage of this method is that the reconstruction and simplification processes can be integrated as a whole. Experimental results show that the proposed method is faster with better robustness.

KeywordsSimplifyDense point cloudMesh reconstructionOutward expansion

收稿日期：2015-01-14。国家高技术研究发展计划项目(2013AA 10230402)；中央高校基本科研业务费西北农林科技大学科技创新项目(QN2013054)。董天琪，硕士生，主研领域：计算机图形学。张志毅，副教授。

中图分类号TP391.41

文献标识码A

DOI:10.3969/j.issn.1000-386x.2016.06.063