基于爬山搜索的高斯模糊不变SIFT算子
付 波 张 敏 赵熙临 李超顺
1(湖北工业大学电气与电子工程学院 湖北 武汉 430068)2(华中科技大学水电与数字化工程学院 湖北 武汉 430074)
基于爬山搜索的高斯模糊不变SIFT算子
付波1张敏1赵熙临1李超顺2
1(湖北工业大学电气与电子工程学院湖北 武汉 430068)2(华中科技大学水电与数字化工程学院湖北 武汉 430074)
摘要针对SIFT算子对于高斯模糊环境下的特征匹配困难,提出基于目标图像形变空间重采样的高斯模糊不变SIFT算子GI-SIFT(Gaussian Invariant SIFT)。首先构建清晰目标的高斯模糊模型,重采样模型参数重建目标图像完备形变空间;其次,引入降采样与爬山法,构建目标图像的降采样形变空间,在降采样空间中以大采样步长快速搜索当前峰值,对峰值邻域进行曲线拟合,快速找到最优匹配。实验结果表明,所提算法不仅对高斯模糊目标能较好匹配,同时较大提升了目标的特征匹配效率。
关键词尺度不变特征变换形变空间重采样高斯模糊降采样爬山法特征匹配
0引言
高斯模糊形变常见于图像复原领域中[1,2],由于其点扩展函数较难检测,故特征提取与辨识较为困难。SIFT算子[3,4]信息量丰富,独特性好且可扩展性强,具有旋转、尺度、亮度变化等不变性,并对于视角变化、仿射变换、噪声有一定的稳定性[5],广泛应用于各类图像工程领域。例如运动目标跟踪与检测[6,7]、雷达影像配准[8]、红外目标跟踪[9]、手背静脉识别[10]等。
目前,多畸不变SIFT分为两类。一类关注关键点局部区域特征模型与描述,如Harris-Affine[11]、MSER[12]、Hassian-Affine[13]等。刘向增等[14]针对大角度旋转提出基于改进奇异值分解的仿射不变SIFT;Wang等[15]认为SIFT仿射不变性弱的原因在于DoG对关键点的关注区域是圆形,提出用MSER算子代替DoG算子;Zhao等[16]预估目标翻转类型,使翻转区域标准化,构建F-SIFT算子;Zhou等[17]提出基于采样的局部描述子SLD,使圆形区域随视点变化变成椭圆型区域,提升仿射稳定性。
关键点描述算子通过局部不变性统计特征反映目标的全局不变性,对现实场景中的变形目标匹配能力较弱。Morel等提出另一类基于形变空间重采样的ASIFT(AffineScaleInvariantFeatureTransform)算子[18]。通过重采样逼近仿射形变空间以寻找目标图像的可能投影,大大提高算法的匹配准确度。但由于重构空间计算量较大,限制其应用,需要新的手段提高重构空间匹配效率。
1高斯模糊环境下的SIFT特征匹配
1.1SIFT算法
SIFT特征算法主要包括三个步骤:
1) 特征点检测
(1) 在DoG尺度空间中对检测点及其相邻26个点比较,确保在尺度空间和二维空间检测到极值点。DoG空间由不同尺度图像高斯差分函数卷积得:
D(x,y,σ)=(G(x,y,kσ)-G(x,y,σ))×I(x,y)
=L(x,y,kσ)-L(x,y,σ)
(1)
式中,G为二维高斯核函数;L为图像的高斯尺度空间。DoG空间由高斯金字塔相邻两层相减得到;I(x,y)为图像(x,y)位置处的像素值,其中G为:
(2)
式中τ为高斯分布标准差,即尺度空间因子。
(2)DoG空间中检测到的候选极值点并不一定是真正的极值点,一般进行三维二次函数拟合,精确确定关键点的位置和尺度;引入2×2Hessian矩阵,剔除不稳定边缘响应点;最后使用图像梯度方法为每个极值点求取稳定方向,即对每个极值点的邻域内像素的梯度和方向特征采集,使用36柱直方图统计。直方图峰值代表该极值点处邻域梯度主方向,并将大于主方向峰值80%的方向作为辅方向。至此,检测出的含有位置、尺度和方向的极值点即是SIFT特征点。
2) 特征点描述
SIFT一般采用128维特征向量对每个特征点描述,即在关键点周围4×4窗口内计算8个方向的梯度信息,然后对该向量归一化处理。
3) 特征点匹配
两个SIFT描述子匹配一般采用欧氏距离法,Lowe针对128维特征向量维数较高的问题,对传统k-d树进行了改进。如果最近距离与次近距离的比值小于某个阈值,则认定这是一对匹配点。
1.2ASIFT算法
ASIFT算子构建待匹配图像仿射形变空间,来模拟目标在不同参数的变形。其指出对于任意因视角变化引起的仿射变换,均可得到正定仿射变换矩阵A并且通过奇异值分解变换为:
(3)其中,λ>0表示尺度变化,φ为相机方位旋转角度,Ф∈[0,π),θ=arcos(1/t),t≥1。Rφ与RΦ为相机方位对应的旋转矩阵。
图1为ASIFT仿射形变空间采样规则,SIFT算子具有旋转与尺度不变性,故只需对图1中t与Φ采样,以模拟所有可能的仿射形变。仿射形变空间构建完成后,空间中所有采样图像均与待匹配图像进行SIFT特征匹配。记录最优匹配结果。
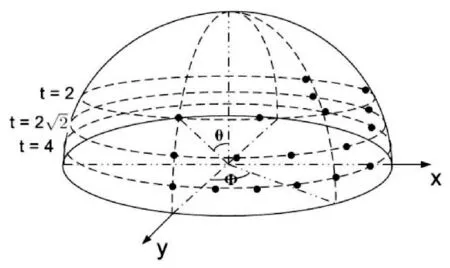
图1 t与Φ的采样规则
1.3高斯模糊环境下的SIFT特征匹配
图像的高斯模糊可通过以下模型实现:
(4)
其中,m、n为二维模板矩阵大小,σ为高斯正态分布标准差,同时也代表模糊半径。
二维高斯函数图像表现为从其中心点开始呈正态分布的同心圆,且离中心越远的像素点权重越小,故二维模板矩阵的大小必须取适当值才能尽量减小计算量,同时保证模糊效果。一般模板矩阵大小取边长为(1+2×3σ)的方阵,即(6σ+1)×(6σ+1),简化计算的同时,也将三个参数m、n、σ减少至一个参数σ。
在高斯模糊环境下,待匹配图像相对于清晰图像来说已十分“平滑”,对高斯模糊目标辨识不利。如图2所示,高斯模糊图像与清晰目标成功配117对,模糊图像自身匹配成功245对,因此有必要提高SIFT算子在高斯模糊环境下的适应能力。

图2 高斯模糊环境下SIFT算子匹配效果对比
2基于形变空间重采样的高斯模糊目标特征匹配
2.1形变空间重采样基本原理
设清晰目标S与待匹配图像T在变换F下匹配建模,首先构造S的形变空间S′:
S′=F{α1,α2,…,αn|S}
(5)
其中,A={α1,α2,…,αn}为模型参数集,n是模型参数个数。对模型参数αi离散化:
αi→{αi1,αi2,…,αim}
(6)
其中,m为重采样点数,由n维离散化模型参数{αij}(i=1,2,…,n,j=1,2,…,m)实现对形变空间的采样,构成重采样空间D逼近原始形变空间S′:
D→S′={D1,D2,…,Dp}
(7)
其中,p=mn,再由Di与T的匹配点数排序得:
D={Df1,Df2,…,Dfp}
(8)
其中,f1…fp是SIFT特征匹配点数从大到小排序,确定最优模型参数组合Af1。该过程实际上是一个优化过程,目标函数:
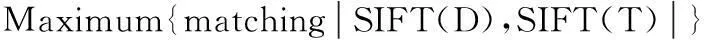
(9)
约束条件:
S′=F{α1,α2,…,αn|S}αi=Ri
(10)
其中,Ri是形变参数空间。
2.2高斯模糊目标特征匹配步骤
GI-SIFT算法流程如图3所示。
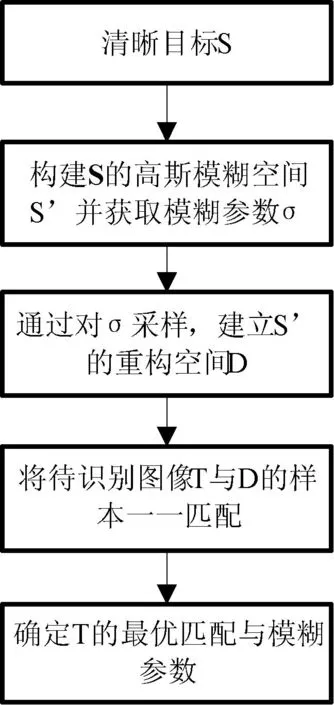
图3 形变空间重采样算法流程
1) 构造清晰目标S的高斯模糊形变空间S′;
2) 设离散模糊参数为σ,构建参数空间Σ={σ1,σ2,…,σm},进而由Σ构建S的高斯模糊重采样空间D={D1,D2,…,Dm}逼近原始形变空间S′,Di为S与高斯模糊核函数F卷积后的图像;
3) 将待匹配图像T与采样空间D匹配,获得目标匹配点数空间P={N1,N2,…,Nm};
4) 空间P中最大匹配点数Nmax对应的样本D*即为所求目标,同时确定T对应的参数σ*。
3基于降采样与爬山法的重采样空间遍历优化
单纯的重采样空间遍历算法,例如ASIFT中所采用的将待匹配图像T与重采样空间D中的所有样本一一匹配。虽然能准确搜寻最大匹配,但计算量过大,如图4所示。
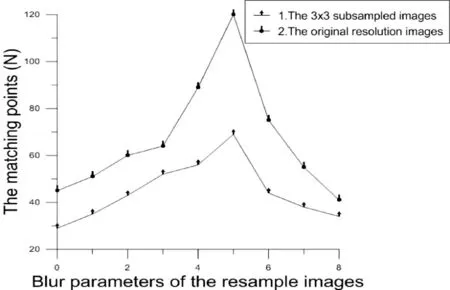
图4 σ=5的待匹配图像与不同分辨率下的重采样空间匹配结果
图4中,待匹配图像T的高斯模糊参数σ0=5,其表示在不同分辨率条件下,模糊图像与清晰目标的N-σ曲线。图中降采样下的曲线1在匹配点数上远远少于原分辨率下的曲线2,但两条曲线的变化趋势却是相同的。N-σ曲线均可看作一幅单峰波形图,说明降采样方法在减少计算量的同时,并不会影响N-σ曲线的走势。
3.1图像降采样
降采样常用于图像特征提取类算法,如SIFT算法DoG图像金字塔的构建采用2×2降采样,但参数过大的降采样会导致图片出现严重的失真。必须选择合适的参数,在保证N-σ曲线趋势不变的同时,减少单幅图像匹配计算量。本文采用3×3的降采样。
3.2爬山搜索
将3×3降采样后的待匹配图像Ts与重采样空间Ds中任意一幅图像进行匹配。通过对高斯模糊参数σ的扰动,判断扰动前后匹配点数N的变化情况,按照使匹配点数N增加的原则在重采样空间中搜索与Ts的最大匹配。该方法思路简单,且易实现。
如图4所示的N-σ曲线,用爬山法能轻易地找出当前曲线的峰值点,但该点可能与真实峰值点有所偏差。本文通过构建N-σ曲线,快速搜索曲线峰值点区域,然后采用局部曲线拟合确定峰值P点。该方法兼具搜索效率高与精确度高的优点。
3.3算法实现
基于降采样与爬山法的重采样空间遍历优化算法流程如图5所示。
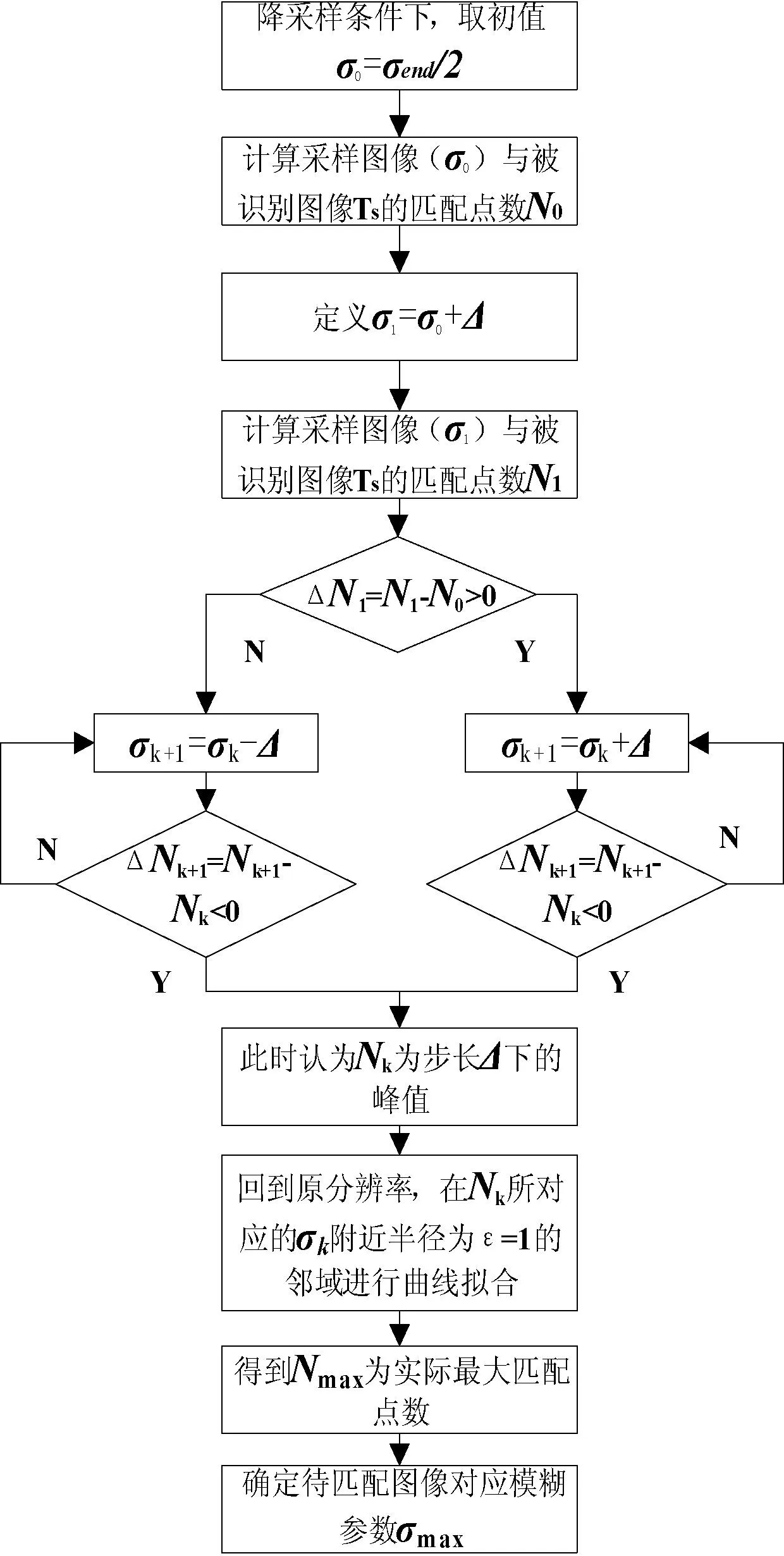
图5 基于图像降采样及爬山法的改进算法流程图
算法实现步骤如下:
1) 以采样步长Δ重构清晰目标S的重采样空间Da,对待匹配图像T,Da进行3×3降采样,得到Ts、Das,将Ts与空间Das中样本的匹配点数N定义为样本模糊参数σ的函数:N=f(σ);
2) 理论上来说,高斯模糊参数σ可以趋近于无穷大,但课题组经过大量实验后发现,当模糊参数σ>8以后,肉眼已难以分辨目标形态,不具备辨识价值,因此本文设置采样参数范围上限阈值σend≤8;
3) 降采样条件下,在步长Δ采样重构空间Das内搜索峰值,令σ0=σend/2,得到匹配点数N0=f(σ0),对σ0扰动,设σ1=σ0+Δ,则N1=f(σ1),匹配点数增量:
ΔN1=N1-N0=f(σ0+Δ)-f(σ0)
(11)
(1) 若ΔN1>0,说明峰值点在σ0右边,继续增加σ,直到σk+1=σk+Δ,如果:
ΔNk+1=Nk+1-Nk=f(σk+1)-f(σk)<0
(12)
则Nk为对应步长Δ下的N-σ曲线峰值;
(2) 若ΔN1<0,说明峰值点在σ0左边,重定义σ1=σ0-Δ,持续减少σ,直到σk+1=σk-Δ,如果:
ΔNk+1=Nk+1-Nk=f(σk+1)-f(σk)<0
(13)
则Nk为对应步长Δ下的N-σ曲线峰值;
4) 此时回到原分辨率,在峰值点Nk对应的σk周围半径为ε的邻域进行曲线拟合,求得拟合最优参数(Nmax、σmax)。
4实验结果及分析
匹配算法运行在IntelCore(TM)2 2.0GHz处理器上,编译环境为VisualStudio2012。课题组在查阅大量文献后发现,目前学术界并没有专门针对高斯模糊形变的SIFT衍生算法,故在此采用标准SIFT算子与GI-SIFT作对比实验。实验采用程序来自RobHess维护的SIFT算法库(http://robwhess.github.io/opensift/)。实验分为高斯模糊环境下的特征匹配效果对比,采样空间遍历算法优化前后的计算效率对比以及实际应用效果对比。
4.1高斯模糊环境下目标特征匹配效果对比
图6、图7采用512×512分辨率的标准lena图像,分别表示模糊参数σ为1、3的模糊图像在三种算法下的匹配结果对比。(a)、(b)分别为SIFT、GI-SIFT对高斯模糊图片的匹配结果,N为匹配点数。实验结果显示,本文提出的GI-SIFT,相比于SIFT在针对高斯模糊图片的匹配点数上,有显著提高。

图6 模糊图像(上)σ=1在经典SIFT算子与GI-SIFT算子的匹配效果

图7 模糊图像(上)σ=3在经典SIFT算子与GI-SIFT算子的匹配效果
同时,课题组采用华盛顿大学GroundtruthDatabase图片库进行实验。该图片库包含24类图片,课题组选取其中巴塞罗那、剑桥、哥伦比亚峡谷、格陵兰等九类图片,每类50张,分别进行随机参数的高斯模糊形变,对两种算法匹配点数均值统计如图8所示。横坐标代表图像的类别,纵坐标代表匹配点数。从统计结果可以看出,对每一类图片,GI-SIFT的平均匹配点数明显高于SIFT。但由于每类图片内容与模糊度的不同,GI-SIFT相对于SIFT的匹配点数提升幅度也不一样,由64.4%到253.3%,平均提升幅度在117.5%左右,说明GI-SIFT对图片的高斯模糊形变匹配效果提高了很多。
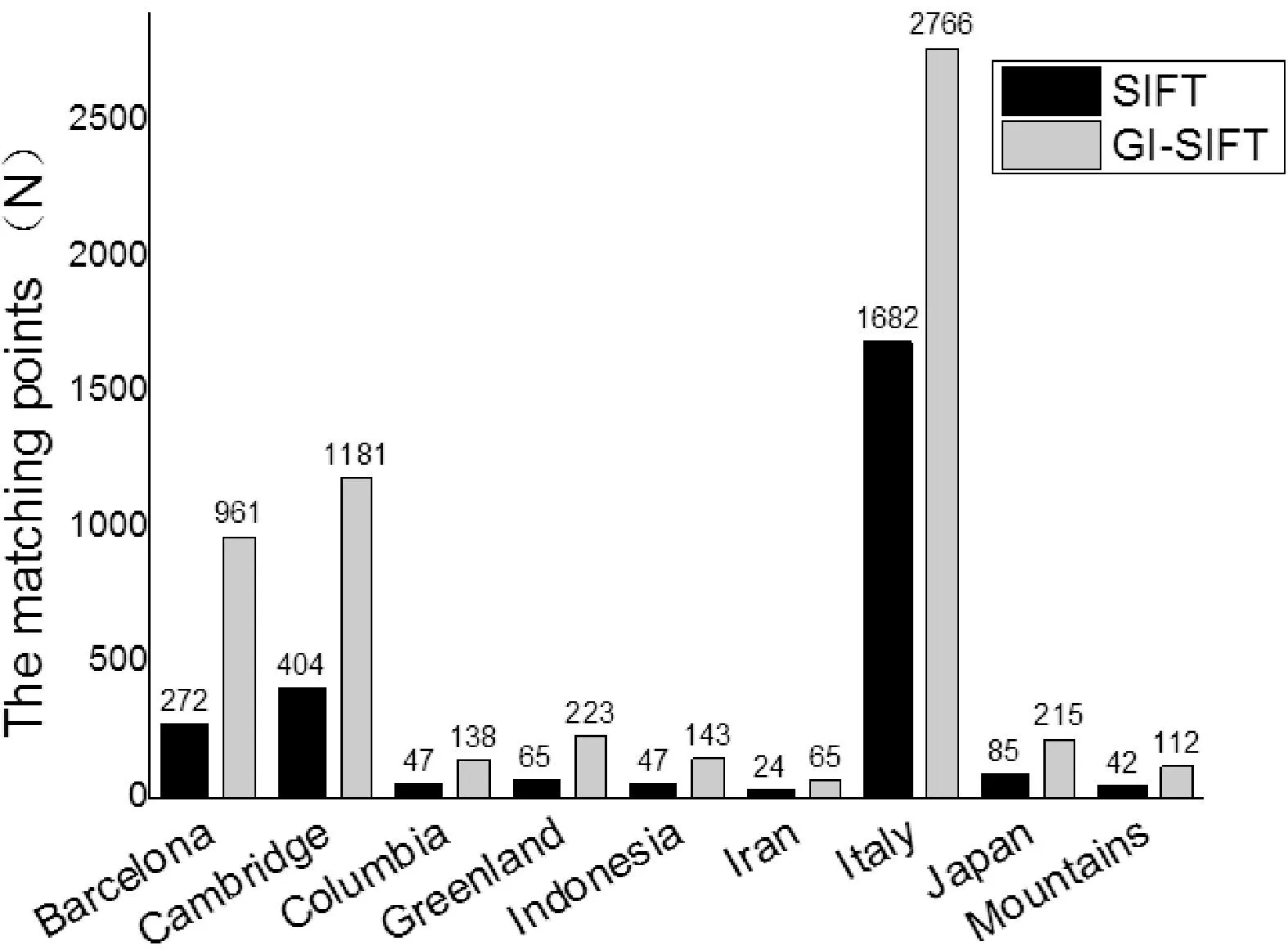
图8 两种算法匹配点数对比
4.2遍历算法优化前后匹配运行时间对比
由于算法的设计思路不同,GI-SIFT在算法效率上与MSER、PCA-SIFT、Harris-Affine等算法并不具有可比性,因此此处只考虑GI-SIFT算法优化前后的时间对比。图9是针对标准Lena图片的高斯模糊特征匹配时间测试,其中邻域半径ε=1,步长Δ=1,σend=8,对目标图像模糊参数σ每隔0.5进行一次时间采样。
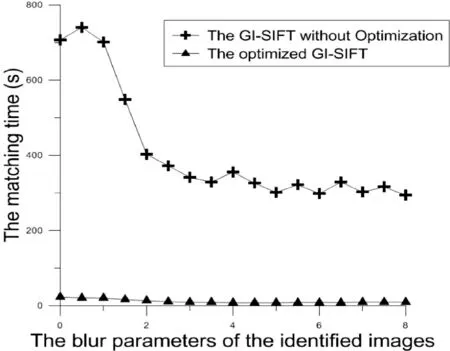
图9 遍历算法优化前后运行时间对比
实验结果显示,当待匹配图像模糊参数在2以下时,匹配时间由优化前的400到750秒缩短至20秒左右;当模糊参数进一步增大时,优化算法所需时间还能够进一步的降低;相对于优化前,GI-SIFT在特征匹配效率上有质的提升,且目标图像的模糊度越小,效率提升越明显。
4.3实际应用效果对比
图10为SIFT与GI-SIFT在实际生活中的应用效果对比。测试图片来自课题组所拍摄的日常照片,其中N为匹配点数。由于日常生活中所遇到的绝大多数图片所受到的均为复合形变,因此并不能完全依照其受到的形变种类来进行绝对的分类。本文在采集实验所用的实际生活照片时,也不可避免会受到光照、视角、焦距等各种因素的影响。但课题组已尽量对除高斯模糊以外的形变进行了限制,以期达到预期的实验效果。 同时,考虑到目标物体被部分遮挡这一情况并不会影响高斯形变的处理效果,在采集实验图片时也加入了目标遮挡这一情况。

图10 SIFT算子与GI-SIFT算子对于实际场景的高斯模糊特征匹配效果
由图10可以看出,(a)、(b)中,待匹配图片模糊度σ1=0.7,目标物体进行了90度的旋转,SIFT算子匹配点数为218,但能明显看出有较多错误匹配点,GI-SIFT的匹配点数为245,且错误匹配点数量没有较大变化。(c)、(d)中,待匹配图片模糊度σ2=1.3,目标物体有一部分被遮挡,SIFT算子的匹配点数为54,GI-SIFT却能找出94个匹配点。(e)(f)中,待匹配图片模糊度σ3=2.7,目标物体有轻微的仿射形变,SIFT算子只能找出5个匹配点,GI-SIFT的匹配点数为13。以上结果说明,本算法在实际应用中也具有较好的匹配效果,与前文实验结果相符。
5结语
针对SIFT算子对高斯模糊环境下的特征匹配能力弱的问题,提出了一种基于图像形变空间重采样的改进算法。通过高斯模糊模型构建待识别目标的重采样形变空间,在该空间内搜寻与待匹配图像具有最大匹配的图像采样,较大提升了特征匹配能力。在此基础上又提出了基于降采样与爬山法的遍历优化算法,在不影响匹配结果的情况下,显著加快运算效率。
参考文献
[1] 陈曦,汪彦刚,彭思龙.部分模糊核已知的混合模糊图像复原算法[J].计算机辅助设计与图形学学报,2010,22(2):272-278.
[2] 王芳,李谊,陆建峰,等.模糊图像盲复原的鲁棒自适应滤波算法[J].计算机辅助设计与图形学学报,2014,26(3):457-464.
[3]LoweDG.Objectrecognitionfromlocalscale-invariantfeatures[C]//ProceedingsofInternationalConferenceonComputerVision.Kerkyra,Greece:IEEE,1999:1150-1157.
[4]LoweDG.Distinctiveimagefeaturesfromscale-invariantkeypoints[J].InternationalJournalofComputerVision,2004,60(2):91-110.
[5] 吴慧兰,刘国栋,刘炳国,等.基于SIFT算法的圆心快速精确定位技术研究[J].光电子·激光,2008,19(11):1512-1515.
[6] 蔺海峰,马宇峰,宋涛.基于SIFT特征目标跟踪算法研究[J].自动化学报,2010,36(8):1204-1208.
[7] 明安龙,马华东.多摄像机之间基于区域SIFT描述子的目标匹配[J].计算机学报,2008,31(4):650-661.
[8] 陈尔学,李增元,田昕,等.尺度不变特征变换法在SAR影像匹配中的应用[J].自动化学报,2008,34(8):861-868.
[9] 郑红,郑晨,闫秀生,等.基于SUKF与SIFT特征的红外目标跟踪算法研究[J].光电子·激光,2012,23(4):791-797.
[10] 王云新,刘铁根,江俊峰,等.基于局部SIFT分析的手背静脉识别[J].光电子·激光,2009,20(5):681-684.
[11]MikolajczykK,SchmidC.Scale&affineinvariantinterestpointdetectors[J].InternationalJournalofComputerVision,2004,60(1):63-86.
[12]ForssénPE,LoweDG.Shapedescriptorsformaximallystableextremalregions[C]//ProceedingsofThe11thInternationalConferenceonComputerVision.RiodeJaneiro,Brazil:IEEE,2007:601-614.
[13]RuanL,SridhaS,ClintonF.Hessian-Basedaffineadaptationofsalientlocalimagefeatures[J].JournalofMathematicalImagingandVision,2012,44(2):150-167.
[14] 刘向增,田铮,温金环,等.基于仿射不变SIFT特征的SAR图像配准[J].光电工程,2010,37(11):121-127.
[15]ZhupingWang,HuiyuMo,HanWang,etal.AnAffineInvariantFeatureDetectionMethodBasedonSIFTandMSER[C]//Proceedingsof2012 7thIEEEConferenceonIndustrialElectronicsandApplications(ICIEA).Singapore:IEEE,2012:69-72.
[16]WanleiZhao,ChongwahNgo.Flip-InvariantSIFTforCopyandObjectDetection[J].IEEETransactionsonImageProcessing,2013,22(3):980-991.
[17]WenZhou,ChunhengWang,BaihuaXiao,etal.SLD:ANovelRobustDescriptorforImageMatching[J].IEEESignalProcessingLetters,2014,21(3):339-342.
[18]MorelJM,YuG.ASIFT:anewframeworkforfullyaffineinvariantimagecomparison[J].SIAMJournalonImagingSciences,2009,2(2):438-469.
GAUSSIAN BLUR INVARIANT SIFT OPERATOR BASED ONHILL-CLIMBINGSEARCHING
Fu Bo1Zhang Min1Zhao Xilin1Li Chaoshun2
1(School of Electrical and Electronic Engineering,Hubei University of Technology,Wuhan 430068,Hubei,China)2(School of Hydropower and Information Engineering,Huazhong University of Science and Technology, Wuhan 430074,Hubei,China)
AbstractSIFT operator is difficult in feature matching in Gaussian blur environment. Aiming at this problem, we proposed a Gaussian blur invariant SIFT operator (GI-SIFT) which is based on resampling in deformation space of object image. First, we built the Gaussian blur model of the clear object and re-sampled the model parameters to reconstruct complete deformation space of the object image. Secondly, we introduced subsampling and hill climbing approaches to construct the subsampling deformation space of the object image, and rapidly searched the current peak value in subsampling space with large sampling step, and made curve fitting in peak neighbourhood to quickly find the optimal matching. Experimental results showed that the proposed algorithm can well match Gaussian blur object, at the same time it also greatly improves the efficiency of objects feature matching.
KeywordsScale invariant feature transform (SIFT)Resampling of deformation spaceGaussian blurSubsamplingHill-climbingFeature matching
收稿日期:2014-12-18。国家自然科学基金项目(61072130,5110 9088);武汉市科技攻关计划项目(2013012401010845);湖北工业大学科研基金项目(BSQD12107);广东省工业攻关项目(2011B010100037)。付波,教授,主研领域:图像处理。张敏,硕士生。赵熙临,副教授。李超顺,副教授。
中图分类号TP391.4
文献标识码A
DOI:10.3969/j.issn.1000-386x.2016.06.045

