基于动态T检验的修正最小二乘BFGS定位算法

孟　娟　洪　利　李亚南　韩智明

(防灾科技学院防灾仪器系　河北 三河 065201)



基于动态T检验的修正最小二乘BFGS定位算法

孟娟洪利李亚南韩智明

(防灾科技学院防灾仪器系河北 三河 065201)

摘要针对传统基于接收信号强度指示RSSI(Received Signal Strength Indicator)的最小二乘定位算法精度有限的问题，从降低信号噪声影响出发，提出一种基于动态T检验的修正最小二乘-BFGS定位算法。在测距阶段，将T检验法动态应用于RSSI值筛选，以消除较大测量误差影响，提高测距精度；定位阶段，先基于平均测算距离对传统的最小二乘法进行修正，提升初步定位精度0.3～2米；在此基础上，以信号强度误差最小为目标优化函数，基于BFGS算法对修正最小二乘法计算的初值进行迭代求精，以进一步提高定位精度。仿真实验表明，该算法有效提升了定位精度，在100 m×100 m范围内可比传统最小二乘定位误差降低4～11米。

关键词定位算法接收信号强度指示T检验最小二乘BFGS

0引言

随着无线传感器网络在农业、智能家居、物流、采矿等多行业的应用，传感器节点的位置信息变得日益重要，在自动组网、网络监测、网络负载均衡等应用中，都需要用到节点的位置信息，因此传感器的节点定位算法备受关注。传感器的定位算法分为基于测距和距离无关的两大类，其中前者定位精度较高，是目前研究热点。基于测距的定位算法需要先测算节点之间的距离或角度，再利用最小二乘法、最大似然估计法、三边测量法等计算未知节点坐标。常采用的测距技术有基于TOA(电波传播时间)、TDOA(电波传播时间差)、AOA(信道到达角度)、RSSI(接收信号强度)等[1]，其中基于RSSI定位算法具有易实现、无需增加额外硬件、成本低等优点，被广泛应用于传感器网络的节点定位中[2-4]。

为提高定位精度，学术界进行了深入研究，提出了多种基于RSSI的测距/定位算法。在RSSI测距方面，针对由于多径、反射、绕射、散射等因素带来RSSI值波动，导致测距不准的问题，提出了利用均值、高斯、卡尔曼、粒子滤波等滤波器来优化RSSI值的方法[5-7]；但当突发干扰导致某些测量值发生强烈跳变时，仅采用滤波器无法完全消除这些粗大误差带来的影响。在定位算法方面，为提高定位精度，牛顿法[8]、最速下降法[9]、拟牛顿法[10-12]等最优化算法被用于未知节点位置的求精迭代，其中文献[9]利用最速下降法对最大似然估计法获得的初始定位值进行迭代，文献[11]将最小二乘法计算出来的初值，用拟牛顿法对未知节点坐标进行迭代。但文献[9]与文献[11]中均以节点的位置误差最小为目标优化函数，其参考的距离在估算时引入了噪声误差，因此影响了定位精度。

针对以上问题，本文提出一种基于动态T检验的修正最小二乘-BFGS定位算法：在测距阶段，将传统的T检验方法动态运用于测量数据预处理，消除误差较大的跳变RSSI值，将剩余较稳定的RSSI值作为有效值，并利用卡尔曼滤波器进行滤波以提高测距精度；在定位阶段，对传统的最小二乘法进行修正，提高初次定位精度；在此基础上，以信号强度误差为目标优化函数，利用最优化算法中的BFGS算法进行二次定位，求取未知位置最优解。

1测距/定位原理

基于RSSI的测距/定位算法原理是根据无线信号传播模型，将未知节点(接收端)接收到的参考节点(发射端)的RSSI值转化为距离，再根据参考节点位置计算出未知节点坐标。因此，基于RSSI的测距/定位算法分为两步：RSSI测距和基于多参考节点的定位。

1.1RSSI测距

基于RSSI的测距原理是利用无线信号的传播模型，根据接收信号强度得到接收机和发射机距离的估计值。常用无线信号传播模型有自由空间传播模型、M-K模型、Shadowing模型等，在RSSI测距定位算法中常用的为Shadowing模型[13]：

(1)

式中，RSSI(di)为距离发射端di时接收端接收到的信号强度；d0为参考距离；γ为路径损耗指数，由传输环境决定，通常通过测量获取；Xδ是均值为0，方差为δ的正态分布随机噪声。

在实际测量中，一般取d0=1m，并对RSSI值进行处理(如滤波)，使噪声Xδ对测量结果的影响降低到最小甚至忽略不计，则式(1)简化为：

Ri=R0-10γlg(di)

(2)

R0和γ决定了RSSI值与信号传播距离的关系，根据式(2)可估算未知节点与参考节点间的距离：

(3)

1.2基于最小二乘法的节点定位

若未知节点获得3个或3个以上参考节点(AP)的信息，则可采用最小二乘法、最大似然估计法、三边测量法等估算其位置。其中最小二乘法是一种经常采用的方法，其原理如下：假设在待测区域内有m个参考AP，第i个参考AP的位置分别为(xi,yi)，i≤m，未知节点p的位置为(x,y)，据式(3)得到未知节点p到第i个参考AP的距离为di，则可得到下列定位方程组：

(4)

2基于动态T检验的修正最小二乘-BFGS定位算法

2.1算法原理

图1　基于动态T检验的修正最小二乘-BFGS定位算法流程图

由式(2)和式(4)所知，对于确定的无线信号传播模型，RSSI无线定位算法的精确性依赖于接收信号强度的精确度以及由其计算得到的估算距离。但在实际定位过程中，由于受无线信号传输中多径、散射等因素带来的噪声影响，使得式(2)所示的功率关系存在一定误差，从而降低RSSI定位精度。一方面，噪声Xδ使式(2)所示的功率关系存在较大误差，恶化了式(3)所示的距离关系的准确性；另一方面，在最小二乘法定位过程中，通过减去一个参考点方程消去方程组中的二次方变量，若这个被选择的参考点误差较大，则会严重增加整个线性方程组的误差，降低定位精度。本文从这两个方面对传统的RSSI定位算法进行改进，提出了一种基于动态T检验的修正最小二乘-BFGS定位算法，从两个方面减少噪声的影响，以有效提高定位精度：一方面，通过对RSSI测量数据进行动态T检验和滤波，剔除部分高噪声数据，提高测距精度；另一方面，在最小二乘法定位过程中，通过减去定位方程的平均值，降低高信噪定位方程对定位精度的影响。

基于以上思考，本文提出的基于动态T检验的修正最小二乘-BFGS定位算法流程如图1所示。算法首先对T检验进行动态应用，以对测量数据进行预处理，剔除较大误差数据，同时进行卡尔曼滤波，使RSSI强度测量值更加稳定可靠；其次，对数据进行基于最小二乘法的初定位，通过减去所有参考方程的平均值减少定位误差；最后，将目标节点的定位问题转化为以信号强度误差最小为优化函数的非线性无约束优化问题进行求解。

2.2RSSI数据预处理-动态T检验

由于客观条件影响或突发干扰，某些RSSI值偏离真实值，需对这样的数据进行筛选。误差剔除有多种方法，如Grubbs检验、T检验、莱依特检验等。实际测量时，每个测量点测量次数约50次，根据文献[14]，此时T检验是较优的一种。但传统的T检验法一般用于事后的静态检验处理，而测量数据是动态采集的。为实时对测量数据进行处理，可考虑将传统的统计检验方法进行动态化应用，如文献[15]将Grubbs检验进行了动态应用，采用了一种类似滑动窗口思想，通过动态保持50个测量数据为样本进行检验，从而提高监测数据质量。根据文献[14]，T检验在样本数小于30时应用效果更优，因此本文借鉴文献[15]中的算法思想，同时改进该算法中不对最前面数据进行检验而导致剔除可疑值不彻底的缺陷：首先，获取前30个测量数据，对这些数据进行传统的T检验；其次，将T检验做动态化应用，获取当前最新数据，利用T检验判断该值是否为异常值。若判断为正常则保留该值，否则剔除第一次出现的异常值，而保留连续出现的第二个异常值目的是反映测量过程中因移动或其他原因产生的可能变化。

具体的算法流程如下：

算法1动态T检验算法

Step1获取前30个测量数据。

Step2计算当前n个数据的平均值，查找测量值中与平均值误差最大的测量值Xd，设其为可疑值。

Step5置异常值连续出现标志flag为false。

Step6判断数据是否获取完毕，若完毕则结束算法；否则将窗口移动一位，转Step7。

Step7读取最新测量数据Xj(31≤j≤50)。

2.3RSSI数据滤波

由于随机噪声影响，RSSI测量值仍将在一定范围内上下波动，此时需要引入滤波算法使RSSI测量值更稳定。本文采用卡尔曼滤波法对RSSI值进行优化[5,6]，算法流程如下：

算法2基于卡尔曼滤波的RSSI数据优化

Step1设经过动态T检验后被保留的测量值为Ζ={Ζ1,Ζ2,…,ΖN}。

Step2初始条件：设过程噪声协方差Q=1e-6，测量噪声协方差F=0.01，初值R(1|1)=R(1)，协方差P(1|1)=R(1)。

Step3fromt=2tot=N，计算：

预估信号强度R(t|t-1)=R(t-1|t-1)

预估计协方差矩阵P(t|t-1)=P(t-1|t-1)+Q

卡尔曼增益Kg(t)=P(t|t-1)/(P(t|t-1)+F)

更新信号强度R(t|t)=R(t|t-1)+Kg(t)(Z(t)-R(t|t-1))

更新协防差矩阵P(t|t)=(1-Kg(t))P(t|t-1)。

Step4得到最优估计R(N|N)。

卡尔曼滤波后，根据式(3)估算未知节点与参考AP间的距离，并基于此估算未知节点的位置。

2.4修正的最小二乘法初定位

传统最小二乘法定位时，若被选择的参考AP误差较大，则最终定位结果误差会变得更大。为提高初始定位精度，对传统最小二乘法进行修正：将方程组式(4)中所有方程左右两边相加并取均值，得到：

(5)

将式(4)中所有方程都减去式(5)则得到新方程组：

(6)

2.5修正最小二乘-BFGS定位算法

最小二乘法在定位过程中可能存在非奇异矩阵，导致估算位置误差较大。为提高精度，常利用最优化方法进行未知节点位置的迭代求精[8-12]。BFGS是经典拟牛顿算法，收敛快、计算存储量较小，适合解决中小规模无约束最优化问题。因此,本文选用BFGS算法进行二次定位。

文献[9,11]中，优化函数中的di在计算时引入了噪声影响，因此在定位时会叠加距离测算带来的误差。在修正的最小二乘法求取未知节点初始坐标后，根据式(2)，本文将目标节点定位问题转化为以信号强度误差最小为优化函数的非线性无约束优化问题，即求解式(7)。相比文献[9,11]，本文目标优化函数直接以信号强度为参考，不会叠加距离测算带来的误差，因此可减小定位误差。

(7)

式中(x,y)为未知点的待估算坐标，Ri为未知节点收到的第i个参考AP的信号强度，R0是距离发射端1m时的接收信号强度，(xi,yi)为第i个参考AP的位置。

算法流程如下：

算法3修正最小二乘-BFGS定位算法

Step1利用修正最小二乘法求取未知坐标的初始估计值，将该值作为BFGS迭代求解的初值x0，设误差精度ε≤e-6。

Step2设H0=In(n=2)，计算式(7)中f(x,y)在x0处的梯度g0=▽f(x0)。若g0=0，则算法停止，极小值点为x0；否则转Step3。

Step3令k=0，确定搜索方向为dk=-Hkgk。

Step5计算‖f(xk+1)‖，若‖f(xk+1)‖≤ε，则算法停止，极小值点为xk+1，否则转Step6。

Step6若k+1=n，则令x0=xn，转Step3，否则转Step7。

3仿真分析

为验证本文算法有效性，利用Matlab进行仿真实验与分析，并与传统最小二乘法和文献[11]的最小二乘-拟牛顿定位算法进行对比。

3.1仿真参数设置与相关定义

将传统的最小二乘定位算法记为LS，文献[11]中最小二乘-拟牛顿算法记为LN，本文修正最小二乘算法记为MLS，基于动态T检验的修正最小二乘-BFGS算法记为SMB，不加检验修正最小二乘-BFGS算法记为MB。

最大仿真网络环境设置为100m×100m，在仿真区域随机布置若干个参考AP和k个未知节点，假设无线信号的传播路径损耗因子γ=2，R0=-24.5db，随机噪声满足N(0,δ)(2≤δ≤10)的正态分布。为验证算法稳定性，每种算法均进行100次仿真，以平均定位误差e来分析算法性能，其定义如下：

(8)

3.2结果分析

图2仿真了在不同通信范围内，布置5个参考AP，当噪声满足N(0,10)时的不同算法性能对比。随着通信范围增大，定位误差随之增大。在30m×30m～100m×100m的通信范围内，相比传统最小二乘法，本文修正最小二乘法可减小初始误差约0.3～2m，原因在于修正最小二乘法以平均距离为参考，避免选用误差较大的距离；二次定位后，误差可减少4～11m，与文献[11]的最小二乘-拟牛顿算法相比，平均定位误差要小约1～4.5m。

图2　不同通信范围不同算法的平均定位误差

图3仿真了在100m×100m范围内，布置不同数目的参考AP时的算法性能对比。随着参考AP数的增加，定位误差先快速减小，但当参考AP达到一定数量时，定位精度提高较慢。如图3所示，当参考AP节点数量为8以上时，定位精度提升不明显。这是因为参考AP节点增加时，信号强度误差也随之累加，故最终定位精度不会一直提升。本文算法比传统最小二乘法的误差约降低4～11m，比文献[11]定位误差平均降低1～4.5m。

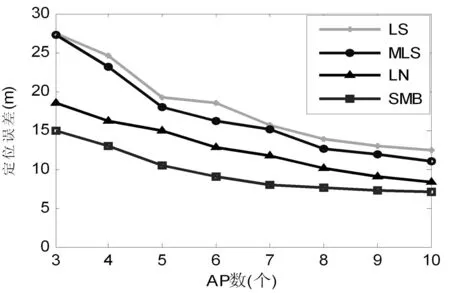
图3　不同AP个数不同算法的平均定位误差

图4仿真了在100m×100m范围内，布置5个参考AP时，在不同的噪声方差δ条件下的不同算法性能。从图中看出，随着δ增加，定位误差增加。但本文算法比传统的最小二乘法的定位误差约小4～11m，比文献[11]平均定位误差降低约1～4.5m。

图4　不同噪声方差不同算法的平均定位误差

图5仿真了在100m×100m范围内，布置5个参考AP时，在不同的噪声方差条件下，是否采用动态T检验的算法性能。从图中看出，采用检验的定位算法比不采用检验的定位算法误差要小，噪声方差越大，加检验后定位误差越低，性能提升0.1%～0.45%。

图5　是否采用动态T检验的算法性能对比

4结语

基于RSSI定位算法中信号噪声的影响，提出一种基于动态T检验的修正最小二乘-BFGS定位算法。在定位之前对测量RSSI值进行了预处理，利用动态T检验消除了异常值的影响，并利用卡尔曼滤波器得到最优RSSI值，从而提高测距精度。相比于未采用动态T检验的定位算法，提高约0.1～0.45m的定位精度。定位时，先利用平均测算距离对传统的最小二乘法进行了修正，初步提升定位精度0.3～2m；再以信号强度误差为目标优化函数，结合最优化方法中的BFGS算法，大大提高定位精度。仿真实验证明，本文算法相比传统的最小二乘法误差降低约4～11m，比文献[11]误差降低约1～4.5m，表明了算法在提高定位精度的有效性和可行性，同时算法无需增加额外的硬件开销，具有较强的实际应用价值。需要说明的是，由于采用了检验和滤波的方法对RSSI测量数据进行处理，因此本文算法需要较多的RSSI测量数据进行处理，因此本文算法适用于节点相对静止或低速运动状态下的定位。课题组下一步将对如何提高节点高速运动下的定位精度进行研究。

参考文献

[1]VianiF,RoccaP,OliveriG.Localization,tracking,andimagingoftargetsinwirelesssensornetworks:Aninvitedreview[J].RadioScience,2011,46(5).

[2] 刘雪兰,王宜怀,陆全华,等.无线传感器网络RSSI定位算法改进[J].计算机应用与软件,2013,30(11):87-89,141.

[3]XiuyanZhu,YuanFeng.RSSI-basedAlgorithmforIndoorLocalization[J].CommunicationsandNetwork,2013,5:37-42.

[4] 胡志坤,蒋英明,王文祥,等.基于ZigBee的井下人员精确定位方案及实现[J].计算机应用与软件,2013,30(5):159-162,170.

[5]AnindyaSPaul,EricAWan.RSSI-BasedIndoorLocalizationandTrackingUsingSigma-PointKalmanSmoothers[J].IEEEjournalofselectedtopicsinsignalprocessing,2009,3(5):860-873.

[6]RungchingChen,YuHsiangLin.ApplyKalmanfiltertoRFIDReceivedSignalStrengthprocessingforindoorlocation[C]//IEEE2012 4thInternationalConferenceonAwarenessScienceandTechnology,21-24Aug,Seoul,Korea,2012:73-77.

[7] 刘兴川,张盛,林孝康.基于数据融合的WLAN/MARG组合定位系统[J].系统工程与电子技术,2012,34(11):2361-2365.

[8] 姚金杰,韩焱.基于粒子群和牛顿迭代法的目标定位方法研究[J].计算机应用研究,2010,27(5):1710-1713.

[9] 石琴琴,霍宏,方涛,等.使用最速下降算法提高极大似然估计算法的节点定位精度[J].计算机应用研究,2008,25(7):2038-2040.

[10]FangZhao,HaiyongLuo,HaoGeng,etal.AnRSSIGradient-basedAPLocalizationAlgorithm[J].ChinaCommunications,2014,11(2):100-108.

[11] 程秀芝,朱达荣,张申,等.基于RSSI差分校正的最小二乘-拟牛顿定位算法[J].传感技术学报,2014,27(1):123-127.

[12]BenjianHao,ZanLi.BFGSquasi-NewtonlocationalgorithmusingTDOAsandGROAs[J].SystemsEngineeringandElectronics,2013,24(3):341-348.

[13]VianiF,LizziL,RoccaP,etal.ObjecttrackingthroughRSSIMeasurementinwirelesssensornetworks[J].ElectronicsLetters,2008,44(10):653-654.

[14] 王文周.未知σ,t检验法剔除异常值最好[J].四川工业学院学报,2000,19(3):84-86.

[15] 汪宏峰,肖军,何俊,等.车载辐射在线监测系统数据动 态检验处理方法研究[J].核电子学与探测技术,2013,33(7):881-885.

MODIFIED LEAST SQUARES-BFGS POSITIONING ALGORITHM BASEDONDYNAMICT-TEST

Meng JuanHong LiLi Ya’nanHan Zhiming

(Department of Disaster Prevention Instrument,Institute of Disaster Prevention,Sanhe 065201,Hebei,China)

AbstractConventional least-squares (LS) positioning algorithm based on received signal strength indicator (RSSI) has limitation in positioning precision. In view of this, from the perspective of reducing the impact of signal noise, we presented a dynamic T-test-based modified least squares-BFGS positioning algorithm. In stage of RSSI ranging, in order to eliminate the influence of larger measurement errors and to improve measuring precision, we applied the T-test to RSSI values screening dynamically. In stage of positioning, we first modified the conventional LS algorithm based on average estimation distance to enhance the initial positioning accuracy by 0.3～2 meters. On this basis, we took the minimisation of signal strength error as the function of target optimisation, and made iterative improvement on the initial value calculated by modified LS algorithm based on BFGS algorithm to further improve positioning accuracy. Simulation experimental results showed that the algorithm effectively improved the positioning accuracy, compared with conventional LS positioning algorithm, its error decreased by 4～11meter in a range of 100 m×100 m.

KeywordsPositioning algorithmReceived signal strength indicator (RSSI)T-testLeast-squares (LS)BFGS

收稿日期：2015-05-06。中国地震局星火科技计划项目(XH140 72)。孟娟，讲师，主研领域：无线传感器网络，嵌入式。洪利，教授。李亚南，硕士。韩智明，硕士。

中图分类号TP301.6

文献标识码A

DOI:10.3969/j.issn.1000-386x.2016.06.031