样条函数在构造债券收益率曲线中的应用
杨 柳
(复旦大学软件学院 上海 201203)
样条函数在构造债券收益率曲线中的应用
杨柳
(复旦大学软件学院上海 201203)
摘要针对债券市场上芜杂的行情数据,提出将DBSCAN聚类算法应用于构造债券收益率曲线样条函数。通过运用DBSCAN算法对用于构造债券收益率曲线的行情数据进行聚类分析,能够有效地剔除市场上的异常交易数据。在聚类分析结果的基础上,再次应用DBSCAN算法于构造债券收益率曲线,根据市场上行情数据的密集区域对样条函数进行分段。此外,针对传统的依赖于经验进行债券收益率曲线样条函数分段点选取的缺点,使用DBSCAN算法可有效地提高债券收益率曲线和行情数据的符合程度。实验结果表明,将DBSCAN算法用于构建债券收益率曲线样条函数,可以提高收益率曲线反映利率期限结构波动及准确性的效果。
关键词债券收益率曲线样条函数聚类分析DBSCAN算法利率期限结构
0引言
债券作为一类固定收益证券,是资本市场的重要组成部分,债券收益率曲线对社会经济的发展及金融体系的完善起着重要的作用。随着中国资本市场的逐步完善,对于债券收益率曲线也受到了市场前所未有的关注。
市场上债券的交易存在着流动性偏差以及操作方式多样化的特点。券商需要知道随市场波动的债券价格以开展业务操作,因此必须对尽可能多的债券进行估值。将市场上的行情数据引入样条函数,构造债券收益率曲线,并保证曲线的连续性以及平滑性,可以更为合理地对市场上发行的债券进行估值。从收益率曲线构造模型的研究角度出发,可以分为静态模型和动态模型两类[1]。从国际上债券估值的经验来看,美国和日本的央行使用的曲线模型是根据Fisher、Nychka和Zervos提出的,基于McCulloch三次样条函数的三次平滑样条函数;英国央行的曲线模型使用的是基于平滑样条的VRP(VariableRoughnessPenalty)方法,Waggoner(1997)地将平滑样条常数粗糙度惩罚项优化为可变的粗糙度惩罚项[2];除英国以外的其他欧洲国家则都采用的是NS模型或者是NSS模型,NS模型的主要特点就是简洁,对于简单的收益率曲线,能够较好地估计它的形态[3],但是曲线的拟合程度并不高,特别是用于较为复杂的期限结构,所以Svensson扩展了NS模型,即NSS模型,它能够有效地提高曲线拟合的效果[4]。除此以外Hermite差值方法在国际上也有机构使用,比如美国的财政部。从上述国际机构使用收益率曲线构造模型的情况来看,基本上大部分的国际机构都选择使用了静态模型,并且资本市场越是发达的国家,越是偏向于使用样条函数构造收益率曲线。
传统的样条函数分段处理方式中,分段点的选取通常依赖于经验,并且分界点通常取1、3、5等[5],债券的性质决定债券市场的交易具有局部性的特点,传统的处理方式不能随着市场的变动调整样条函数参数数量,即曲线的拟合程度不足。针对以上不足,本文利用债券交易局部性的特点,利用DBSCAN算法对样条函数进行分段,DBSCAN算法是一种较为常见的基于密度的聚类方法[6], 聚类分析是数据挖掘的常用的方法之一,数据挖掘就是从大量的市场交易数据中提取包含在其中的隐藏的知识的过程。能够识别出运营数据中的孤立点,去除噪音,消除数据中的不一致[7]。董乐在研究债券流动性溢价的问题的时候使用了聚类方法进行样本筛选[8],将聚类结果用于债券溢价模型[9,10],虽然聚类在该过程中属于一个辅助的过程,却增加实验结果的可信度。许瑾在研究资产定价模型问题时使用聚类分析方法对研究对象进行分类[11],证明聚类分析在辨别数据有效性时具有较好的效果。特别是DBSCAN算法,它的优点是能够发现任意形状的聚类簇,聚类算法执行速度较快以及不受数据录入顺序的影响,用来根据市场上的交易数据来拟合债券收益率曲线,提高收益率曲线反映债券利率期限结构波动情况及其准确性。
1债券收益率曲线拟合数据分析
用于构造债券收益率曲线的数据往往过多地依赖于人为判断,因此债券收益率曲线拟合时,拟合程度与光滑程度之间的平衡直接受制于人为因素,除此以外,现有市场债券收益率曲线发布的现状不能满足数据的实时性要求。所以如何通过应用数据挖掘技术来改善上述问题,降低人为因素对于债券收益率曲线准确性的影响、缩短市场和债券收益率曲线发布之间的响应时间成了本文解决的问题。
2样条函数的应用过程
目前市场上发布债券收益率曲线的机构每日只在市场收盘时发布一次,比如中国在债券收益率曲线编制方面最具影响力的公司——中国债券登记结算有限公司,也仅仅在每日盘终向市场发布数据。从某种程度上而言,用债券收益率曲线来反映债券市场波动,在时效性方面是不足的,特别是除了“11超日债”成为了中国债券历史上首例违约的事件之外,还有类似于“PR青州债”在盘中被交易所公告“重大事项未公布,暂停交易”的情况发生。可以认为中国债市也同样存在风险,捕捉市场对于风险的反映往往比给风险定价更为重要。目前为止国内大部分的研究都集中于提升收益率曲线模型有效性,而轻于数据的处理,个人认为,数据的准确性比模型的可用性更为重要,所以债券收益率曲线拟合的效果受到用于拟合曲线的行情数据处理效果的影响。
虽然DBSCAN算法在执行时需要预先制定相关参数,并且也存在诸如OPTICS算法对于该方面进行了改进[12],但是在拟合债券收益率曲线时,本文却使用了DBSCAN算法。现代金融学虽然是建立在理性人假设基础之上的,但是金融市场在理论实践方面仍然是个弱有效的市场,所以在样条函数应用过程中,使用聚类算法必须将经验效用纳入考量范围,因此使用预先制定参数的DBSCAN算法更为合适。
2.1DBSCAN聚类算法及交易数据筛选
对几个基本的密度聚类算法的定义做以下简单的介绍。
(1) ε领域
对于给定的数据点p,其半径长度为ε内的区域称为该数据点的ε领域。
(2) 核心对象
假设MinPs为某数据点ε领域内,最少包含的MinPs个数的数据点。
(3) 密度可达
假设数据点集Ω,如果存在一组数据点p1,p2,…,pn;p1=a;pn=b,对于任意的pi,1≤i≤n都存在一个数据点pj,i≠j的ε领域εj,使得pi∈εj,那么则称数据点a与数据点b密度可达。
(4) 噪音的定义
基于密度可达的最大的ε领域的集合称之为簇,如果存在一个数据点p∈Ω,p不属于任何一个簇,则该数据点p被称之为噪音。
数据挖掘中的DBSCAN算法是基于密度的聚类算法中一个非常典型的聚类算法, 能够发现任意形状的聚类。基本思想是:在数据点集Ω的某一个点p,如果要判断它是否归于某一个簇,在点未分配到某个簇的时候,首先判断点p是否为核心对象,若p是核心对象,就对点p的ε领域进行查询,查询出所有密度可达的数据点,形成密度连通集。重复迭代该过程,得到所有的密度连通集,最后剩下的不属于任何密度连通集的数据点就被称为噪音。DBSCAN算法的特点是由核心对象向周围进行搜索,用以保证密度连通逐个形成[6]。DBSCAN算法通过索引相邻数据点,对于全部的数据点只索引一次,加快索引速度。在选择下一个待处理的数据点前,排除当前ε领域内的点,减少重复查询的次数[13]。
在行情交易数据筛选中使用密度聚类的过程就是,首先基于历史数据找出在发生行情的债券剩余期限附近的价格波动区间,在区间之外的可以认为是异常数据;然后在异常数据附近寻找临近的数据点,如果低于某个阈值,就可以认为该数据为噪音。密度聚类的目标就是提供给样条函数用于收益率曲线拟合的有效行情数据,过滤掉异常行情数据,进一步缩小样条函数拟合数据的范围,提高拟合曲线效率。使用密度聚类为样条函数进行数据准备,首先要去掉那些明显的异常行情数据,即行情数据中的孤立点。其次计算对应收益率曲线在该债券剩余期限处20天内的标准差,如果这个债券的交易行情的值在6倍标准差之外,或者在临近该债券剩余期限的范围之内及2倍标准差之内,不存在其他的交易行情数据,这样的行情记录可以删除,如图1所示。
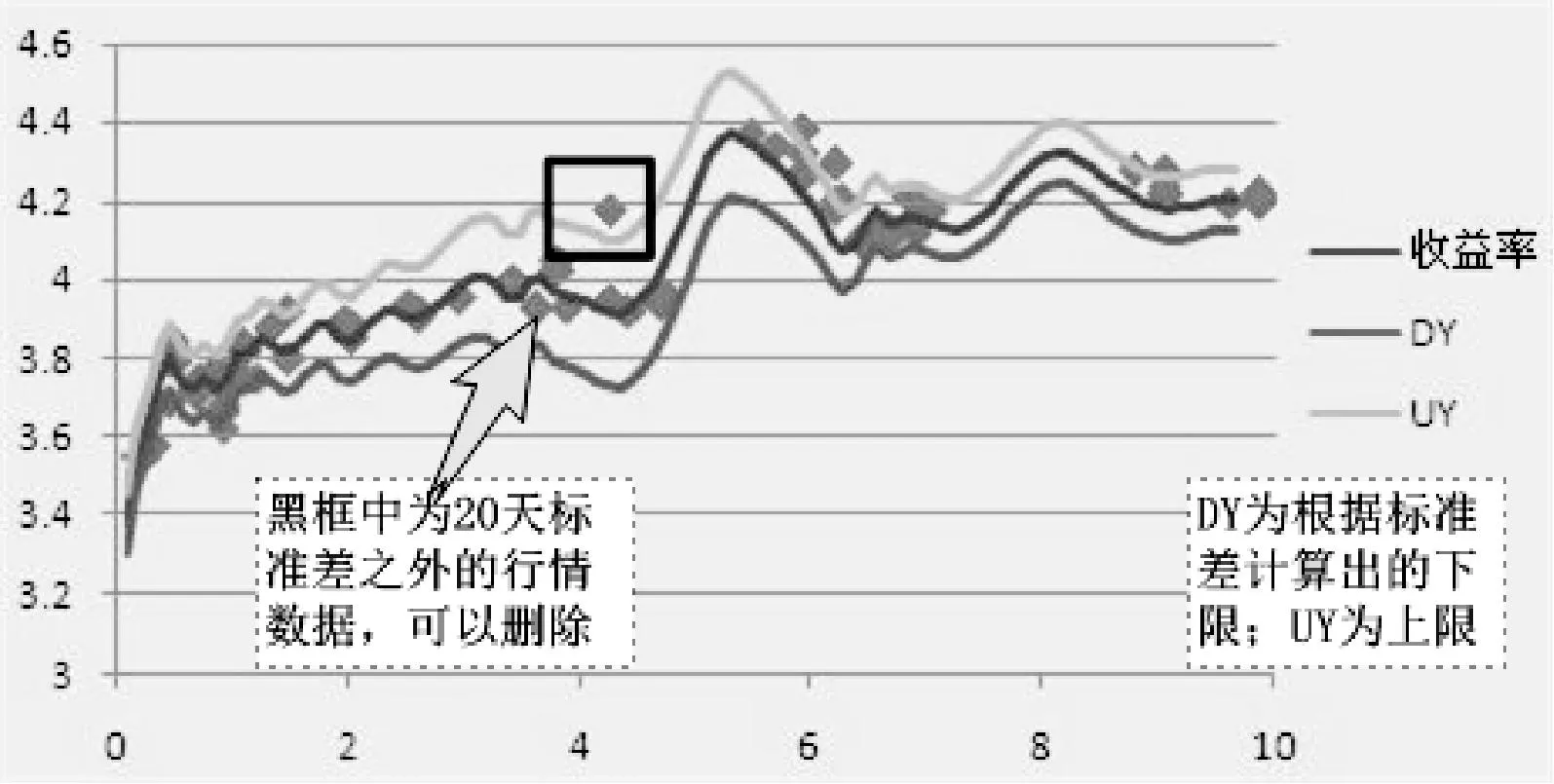
图1 数据准备中删除数据示意图
2.2样条函数分段点的选取
在上述对于将DBSCAN算法用于判断异常数据是否为噪音,将该算法还可以用于在有效行情中判断分界点。
(1) 根据经验指定收益率曲线分界点
根据陈震构造收益率曲线的结论[5],首先按照债券期限结构进行经验上的分段点的选取。一年内的债券为到期债券密集的区域,每0.1年设置一个分界点;1至10年为市场上交易比较密集的区域,每0.5年设置一个分界点;10年以上交易量急剧下降,每10年设置一个分界点。
(2) 根据交易密度指定收益率曲线分界点
使用DBSCAN算法,寻找ε为0.01年的行情数据领域,寻找交易数据的密集区域,在经验进行分段的基础上,根据数据密集领域再次进行分段。
除此以外,随着市场交易的继续进行,原先被判定为异常交易的附近出现了更多的期限结构上临近的交易行情,则可以认为该区域的行情为合理行情,即孤立点区间交易密度达到密度聚类的下限,该数据将不被剔除。保留高密度区域数据的示意如图2所示。

图2 保留高密度区域数据
2.3样条函数的参数估计
根据债券的价格理论,即债券的估值等于所有未来现金流的现值之和如下:
(1)
其中,Pj为第j个债券的估值价格,Nj为该券现金流的数量,tm为第m笔现金流的剩余期限,Cj(tm)为第m笔现金流的值,D(tm)为tm时刻的贴现函数,经过简化后,可以得到函数式:
(2)
其中Tn为样条函数的分界点。上述公式的标准公式如下:
(3)
其中:
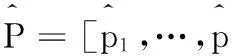
(4)
式中的W是一个对角矩阵,处于计算方便的角度考虑,将债券的权重皆设置成1,矩阵上的每个元素代表相关债券的权重,将债券的久期的导数作为权重如下:
(5)
其中,Duri为第i个债券的久期,三次分段惩罚项的平滑样条需要解决的问题就是:
(6)
这样就转化为一个最小二乘拟合问题,通过迭代拟合求解。
3债券收益率曲线拟合结果分析
3.1与行情数据拟合效果分析
以2013年10月之后将近一个月的国债交易数据为例,采用上述样条模型应用过程进行实证分析。表1市场上实际存在行情数据的债券与其估值价格的偏差分析。
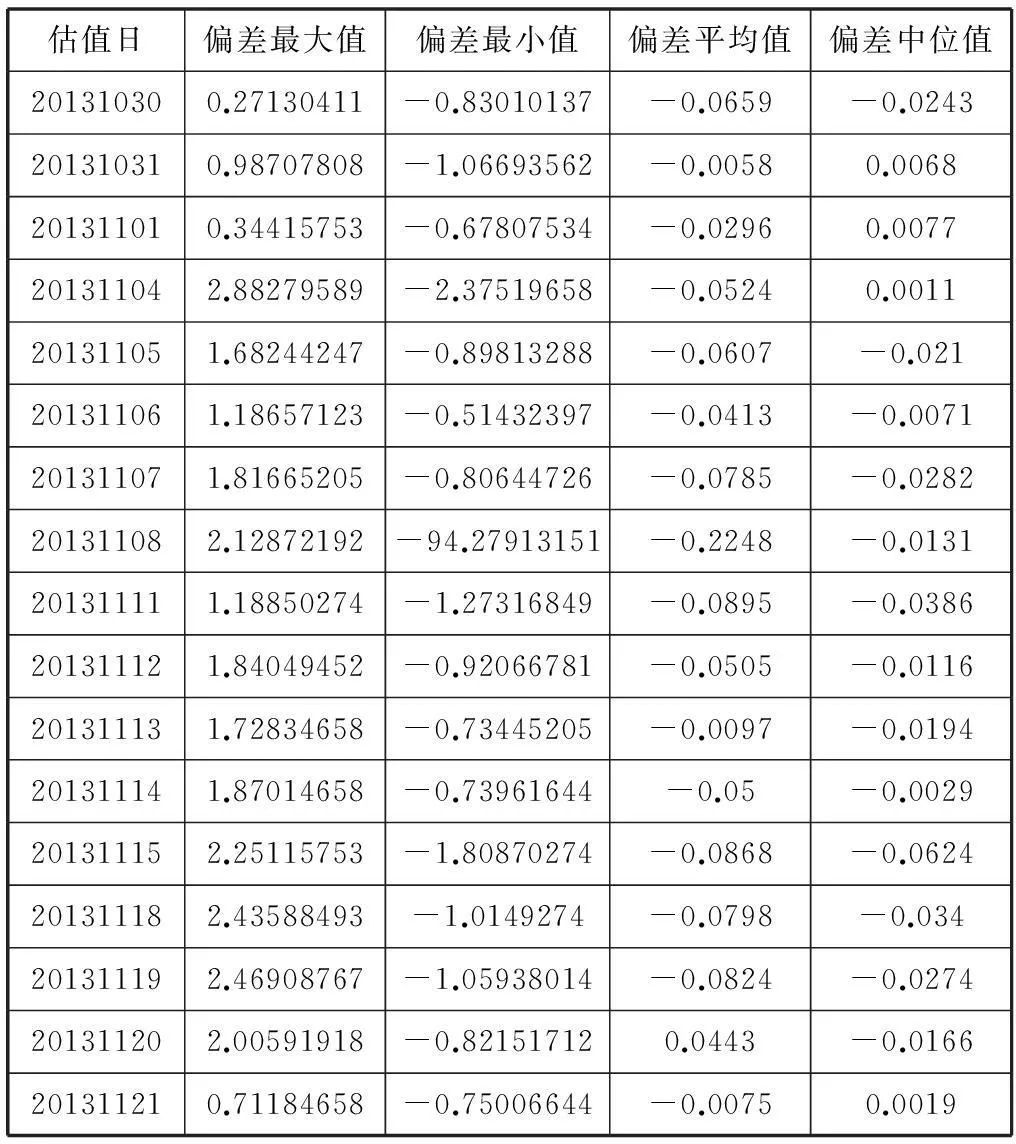
表1 行情价格数据与估值结果偏差统计表
其中估值日为20131108那天,行情偏差最小值存在异常数据,经查证为“光大乌龙指”数据如图3所示。图中圆圈为发生异常债券的期限处,并且在行情收益率曲线拟合的时候已经将该异常数据予以排除,故并未对该期限处的收益率曲线波动造成太大的影响,体现出在异常数据筛选时密度聚类的有效性。从结果中还可以发现,平均的行情数据与估值结果的偏差不足0.1元,所以对市场上存在行情数据的债券来说有很好的估值效果。
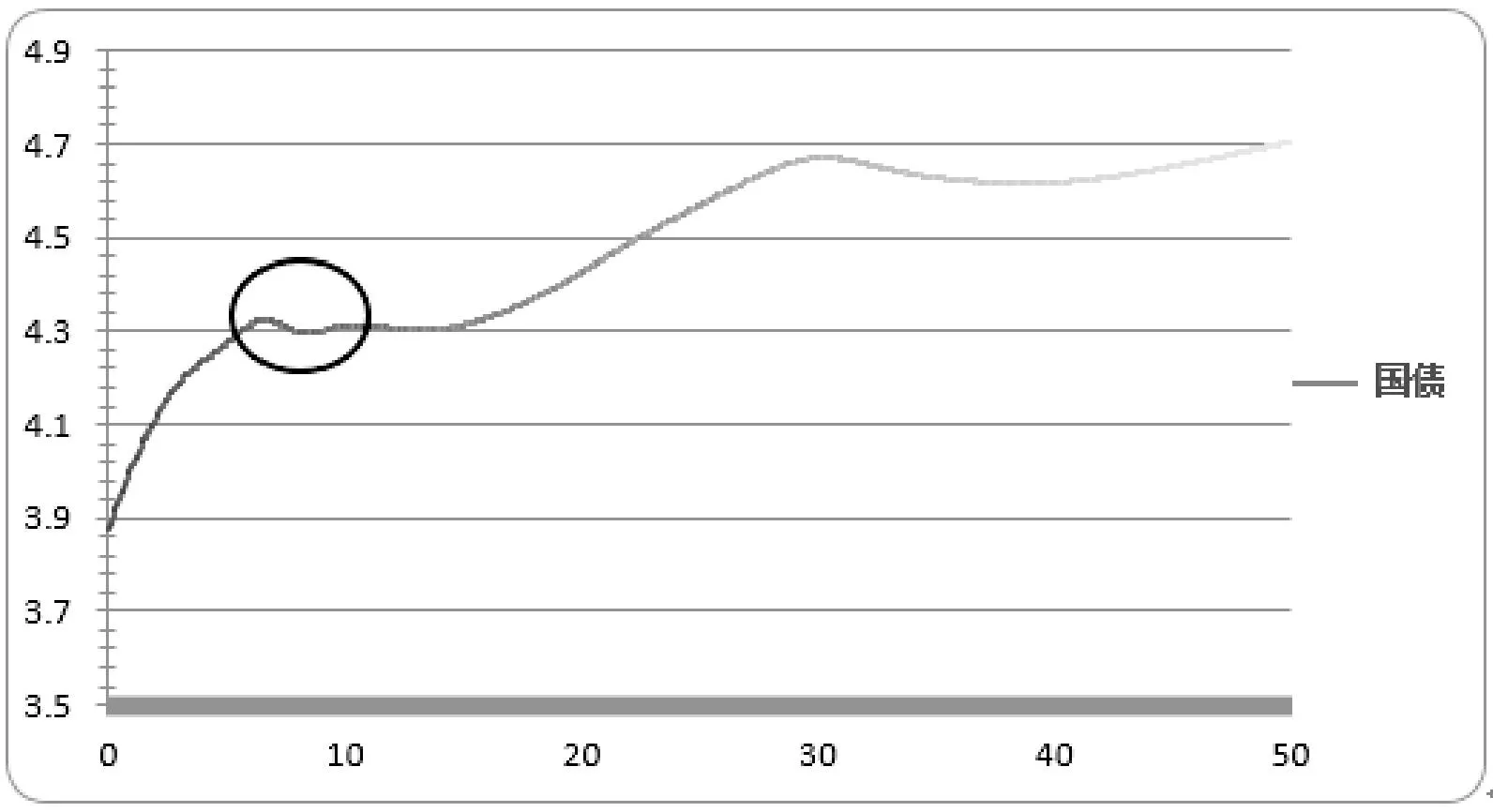
图3 国债收益率曲线生成效果图
从收益率曲线几个关键的期限来看,1年内、1至3年、3至5年、5至于7年以及7至10年之内行情收益率数据与曲线收益率数据的偏差如表2所示。平均收益率的偏差最大在6BP左右,具有较好的拟合效果。

表2 行情价格数据与估值结果偏差统计表
3.2与其他模型生成的收益率曲线数据比对
图4是使用2014年9月12日中国债市行情数据生成的国债收益率曲线效果对比图。Hermite曲线为中债公司使用Hermite插值方法生成的收益率曲线;Splines曲线为本文通过样条函数的应用过程生成收益率曲线。可以看出Splines曲线在10年以内的波动更大,对那一天中国债市的行情数据进行统计得到表3所示。

图4 国债收益率曲线生成效果对比图
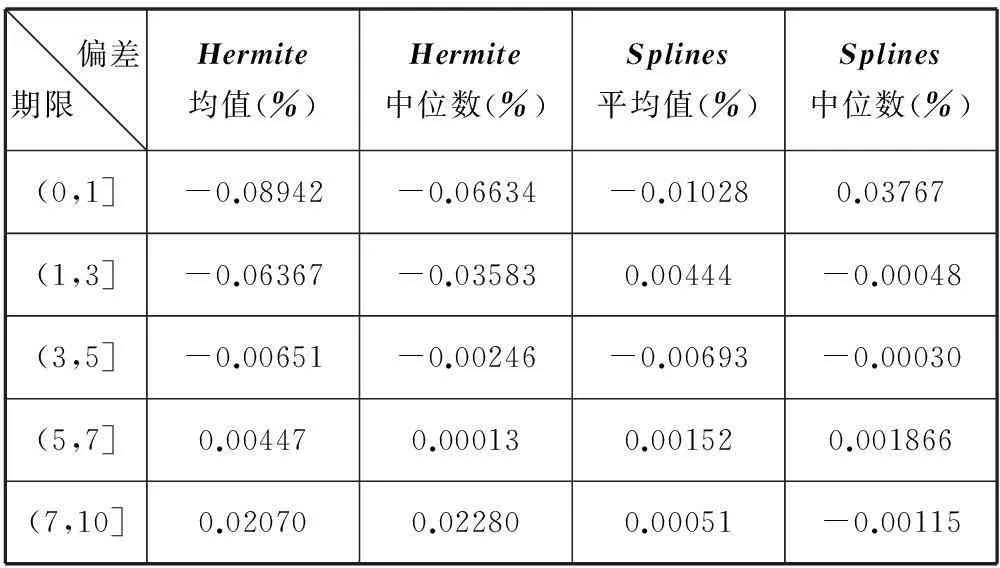
偏差期限 Hermite均值(%)Hermite中位数(%)Splines平均值(%)Splines中位数(%)(0,1]-0.08942-0.06634-0.010280.03767(1,3]-0.06367-0.035830.00444-0.00048(3,5]-0.00651-0.00246-0.00693-0.00030(5,7]0.004470.000130.001520.001866(7,10]0.020700.022800.00051-0.00115
从表3中的统计数据可知,通过样条函数应用过程得到的Splines曲线,虽然在十年之内波动较大,但是它对市场上的债券价格波动拟合程度更好。Hermite曲线在不同期限上,与行情发生价格偏差最大可达到9BP、最小接近0.4BP;Splines曲线最大接近4BP、最小只有0.03BP。Hermite曲线构造的一个重要的问题就是确定用于插值用的数据点,这需要依赖于一个强大的研究团队,这样就无法发挥出数据挖掘的智能性。
将用于拟合Splines曲线的数据用于NSS模型,由于NSS模型的参数个数是确定的,可以使用R程序中的fBonds工具包进行优化求解,得到模型参数估计值,见表4所示。

表4 Nelson Siegel Svensson模型参数估计
将NSS模型拟合收益率曲线的结果与Splines曲线进行比对,就可以发现NSS模型在拟合收益率曲线方面并不见长,特别是在行情波动比较大的区域,如图5所示。
综上所述,在样条函数构造债券收益率曲线的过程中应用密度聚类,可以有效地过滤掉异常数据,并且通过样条函数分段点的选取,可以有效提高与市场债券价格波动的符合程度。
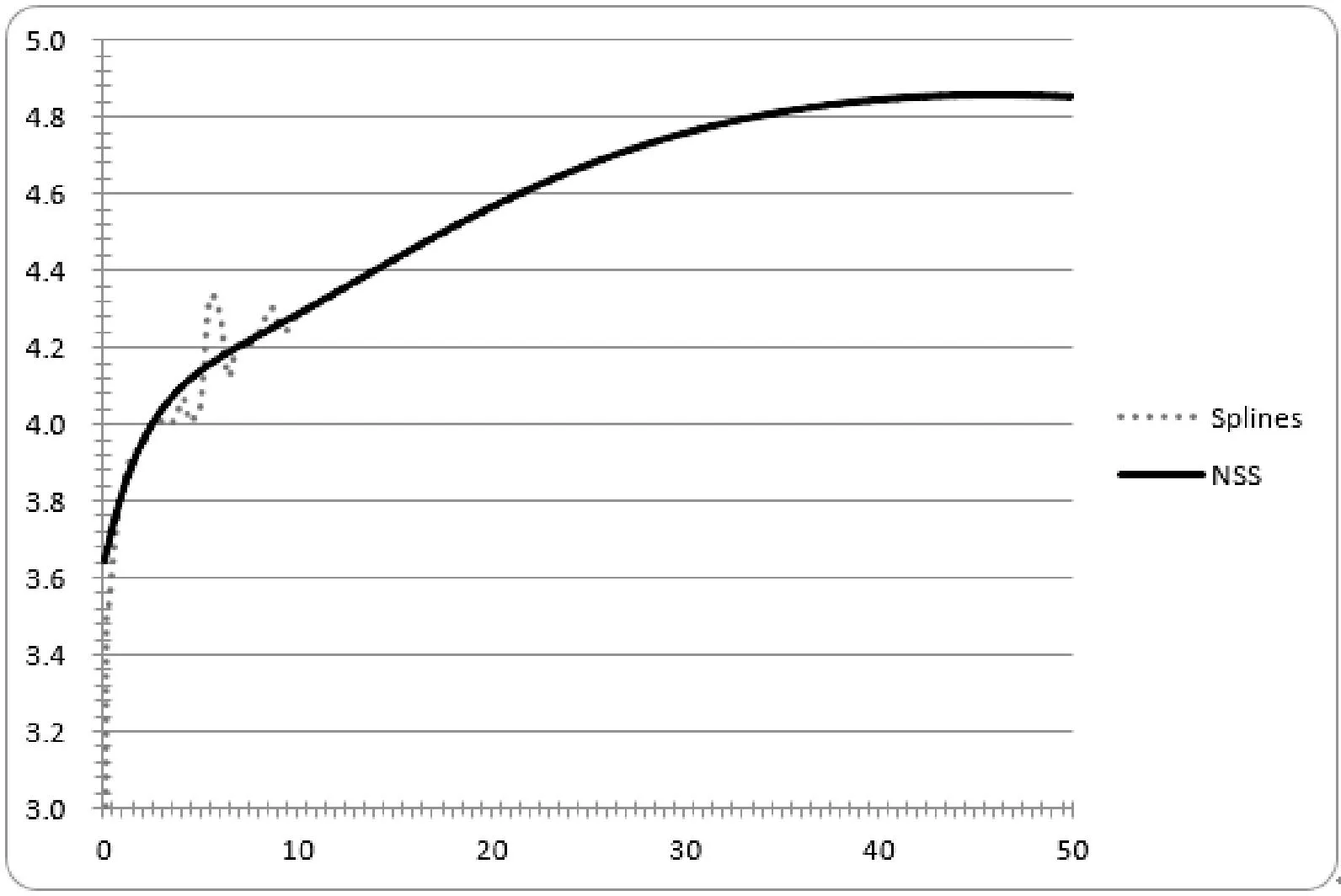
图5 国债收益率NSS模型曲线生成效果对比图
4结语
传统的样条模型分段处理方式中,分界点的选取通常依赖于经验,并且分界点通常取1、3、5等[5]。债券的性质决定债券市场的交易具有局部性的特点,传统的处理方式不能随着市场的变动调整样条模型参数数量,即曲线的拟合程度以及实时性方面存在不足。本文基于DBSCAN算法实现了对于样条模型分界点的自动选取,并在交易不足的区域保留了分段点经验选取的方式,能够在交易密集区提高曲线的拟合程度;在交易稀疏区指导曲线的走向,从而更好地生成符合市场波动的债券收益率曲线。
参考文献
[1]RobertCMerton.Continusous-TimeFinance[M].Wiley-Blackwell,1992.
[2]WaggonerD.Splinemethodsforextractinginterestratecurvesfromcouponbondprices[R].Georgia:FederalReserveBankofAtlanta,1997.
[3]SvenssonLEO.Estimatingandinterpretingforwardinterestrate[R].Sweden:CEPRDiscussionPaperSeries,1994.
[4]SvenssonL.EstimatingforwardinterestrateswiththeextendedNelson&Siegelmethod[R].SverigesRiksbankQuarterlyReview,1995.
[5] 陈震.中国国债收益率曲线研究[D].上海:复旦大学,2009.
[6]KhanK.DBSCAN:Past,presentandfuture,ProceedingsofFifthInternationalConferenceonApplicationsofdigitalInformationandwebtechnologies(ICADIWT),Bangalore,2014[C]//IEEE:Piscataway,2014:232-238.
[7]JiaweiHan,MichelineKamber.Datamining:conceptsandtechniques[M].3rded.ElsevierInc.,2012.
[8] 董乐.银行间债券市场流动性溢价问题研究[J].运筹与管理,2007,16(4):79-88.
[9]TakemataJun,MiyazakiKoichi.TheGRStestforassetpricingmodelsintheJapaneseequitymarket[J].JournalofJapanIndustrialManagementAssociation,2013,64(1):75-84.
[10]DeGiuli,MariaElena.Bayesianoutlierdetectionincapitalassetpricingmodel[J].StatisticalModelling:AnInternationalJournal,2010,10(4):375-390.
[11] 许瑾.统计方法在利率期限结构和多因素资产定价模型中的应用[D].安徽:中国科学技术大学,2005.
[12]AnkerstM,BreunigMM,KriegelHP,etal.OPTICS:orderingpointstoidentifytheclusteringstructure[R].ACMSIGMODRecord,1999,28(2):49-60.
[13] 李双庆.一种改进的DBSCAN算法及其应用[J].计算机工程与应用,2014,50(8):72-76.
[14]WileyFinance.Analysingandinterpretingtheyieldcurve[M].Hoboken:JOHNWILEY&SONSINC,2004.
APPLICATION OF SPLINE FUNCTION IN CONSTRUCTING BOND YIELD CURVE
Yang Liu
(School of Software Engineering,Fudan University,Shanghai 201203,China)
AbstractIn light of the miscellaneous quotation data in bond market, we proposed to apply the DBSCAN algorithm to constructing the spline function of bond yield curve. By employing DBSCAN algorithm to the cluster analysis of the quotation data, which is used to construct bond yield curve, it is able to eliminate effectively the abnormal transaction data on the market. On the basis of cluster analysis results, we used the DBSCAN algorithm once again to construct the bond yield curve, and segmented the spline function into sections according to the dense regions of quotation data on the market. Besides, targeted at the defect of traditional way that it selects the segment points of spline function of bond yield curve depending on experience, the use of DBSCAN algorithm can effectively improve the conformance between the bond yield curve and the bond quotation data. From the experimental results it is illustrated that to apply the DBSCAN algorithm to constructing the spline function of bond yield curve can improve the effects of reflecting the fluctuations of interest term structure by bond yield curve and its accuracy.
KeywordsBond yield curveSpline functionCluster analysisDBSCAN algorithmInterest term structure
收稿日期:2015-01-13。杨柳,硕士,主研领域:数据挖掘。
中图分类号TP311
文献标识码A
DOI:10.3969/j.issn.1000-386x.2016.06.023

