基于压缩感知的视频信号采集观测值渐进量化算法*
杨春玲 刘璇
(华南理工大学 电子与信息学院, 广东 广州 510640)
基于压缩感知的视频信号采集观测值渐进量化算法*
杨春玲刘璇
(华南理工大学 电子与信息学院, 广东 广州 510640)
摘要:在基于压缩感知的视频信号采集中,观测值的量化方法会对重构质量产生重大的影响.为了设计一种性能较优的观测值量化方法,根据视频信号的帧间相关性和压缩感知的视频采集信号观测值特性,提出了基于压缩感知的视频采集信号观测值渐进量化算法.该算法将非关键帧观测值均匀量化后只传输若干不太重要的码平面,在重构端利用邻近的已解码帧通过运动估计生成该非关键帧的边信息帧,再通过观测得到该非关键帧观测值的估计,结合接收到的不太重要码平面信息,通过渐进量化的逆量化得到精确的观测值.实验结果表明:与均匀量化算法相比,文中算法在不增加编码端复杂度和不降低视频序列重构质量的基础上,能大幅降低码率;在相同码率下,不同序列获得的平均增益在0.5~2.0 dB之间,具有较高的率失真性能.
关键词:渐进量化;压缩感知;视频编码
压缩感知(CS)[1- 2]的核心思想是:当信号具有稀疏特性时,可以通过远小于信号长度的少量观测值来精确重构原信号.压缩感知理论实现了信号采样和压缩的同步,利用该理论可大幅减小数据采集量、采样时间、存储及传输负担,因此该理论在信号处理、模式识别、雷达探测、图像压缩与重建等领域受到了广泛的关注[3- 14].
随着压缩感知理论的发展,在图像压缩感知研究[8- 11]的基础上,基于压缩感知的视频采集信号也逐渐成为国内外研究的热点[4- 5,12- 14],但现有算法大多没有考虑观测值量化方法对系统率失真性能的影响.在实际工程应用中,信号在信道中以码流形式传输,对观测值进行量化是必不可少的,然而量化必然会使传输到重构端的观测值精度下降,带来一定程度的率失真性能损失.文献[6- 7]分析了均匀量化应用于压缩感知观测值的低效性,并证明了对随机观测值进行均匀量化会给压缩感知系统带来较严重的性能损失.因此,如何根据压缩感知的观测值特性设计合适的量化方案以提升率失真性能,逐渐引起了学术界的关注.
在图像压缩感知领域,文献[8]将非均匀量化引入心电信号压缩感知,高分辨率区域采用较小量化步长,低分辨率区域采用较大量化步长;文献[9]把差分脉冲编码调制(DPCM)量化方法用于图像分块压缩感知,在观测域对当前块进行预测,并对真实值与预测值的残差做均匀量化;文献[10]在文献[9]的基础上,把DPCM与非均匀量化相结合,根据残差分布特性做非均匀量化.上述研究虽然在一定程度上提升了图像压缩感知系统的率失真性能,但增加了编码端的计算复杂度,违背了压缩感知编码端简单的初衷.文献[11]利用图像压缩感知随机观测值间的隐性相关特性,提出了渐进量化方法.该方法在编码端对均匀量化后的观测值进行分段,第1部分观测值传输完整的量化符号,第2部分观测值只传输若干不重要的码平面信息;在重构端利用第1部分观测值生成第2部分观测值的估计,再与接收到的第2部分观测值的不重要码平面信息结合生成第2部分观测值的较精确估计,最后把两部分观测值合并起来进行压缩感知重构.该量化方法与均匀量化方法的计算复杂度相同,但能有效降低码率,提升率失真性能,是目前图像压缩感知中性能最优的量化方法.
由于视频信号的复杂性,目前研究基于压缩感知的视频采集信号量化方法的文献较少.文献[12]把矢量量化用于分布式压缩感知,并设计了基于均方误差(MSE)最小化的端到端最优映射方法,但该方法增加了编码端复杂度;文献[13]分析了压缩感知随机观测值的分布特性,并根据不同视频序列的均值和方差平均值设计了高斯量化矩阵,但高斯量化不但计算复杂度高,而且对观测值的分布特征有一定的限制,并不适用于所有的视频序列.Liu等[14]研究了基于压缩感知的视频采集信号率失真、采样率、量化精度之间的关系模型,提出了率失真性能优化的自适应视频采集信号比特分配方法.该方法虽然具有一定的普适性,但编码端需进行两次观测,具有编码端复杂度高的缺陷.
鉴于图像压缩感知渐进量化方法在编码端只需要对观测值进行均匀量化并传输量化符号的一部分码平面信息,在不增加编码端复杂度的情况下能有效地提升压缩率这一优越性[11],文中通过分析视频信号压缩感知观测值的特性,把图像渐进量化从图像领域扩展到视频领域,提出了改进的基于压缩感知的视频信号采集观测值渐进量化算法:非关键帧观测值均匀量化后只传输最不重要的码平面信息,重构端利用邻近的已解码帧信息通过运动估计产生非关键帧的近似估计帧(即边信息帧),再进行观测得到非关键帧观测值的估计,结合接收到的不重要码平面信息,通过渐进量化逆量化得到较精确的观测值.
1图像压缩感知渐进量化

1.1渐进量化编码
在编码端,把观测值分为两部分,分别表示为

1.2渐进量化的逆量化
2视频信号采集观测值渐进量化算法
将视频序列划分为长度为p的图像组(GOP),每个GOP的第1帧为关键帧,其余帧为非关键帧.文中提出的基于压缩感知的视频信号采集观测值的渐进量化及其逆量化框图见图1.用高斯随机观测矩阵Φ∈RM×N对关键帧进行观测,得到关键帧观测值Yip=ΦXip,用观测矩阵Φ1(由Φ的前M1(M1≤M)行构成)对非关键帧进行观测,得到非关键帧观测值Yj=Φ1Xj.
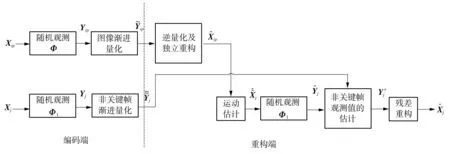
图 1 文中算法的结构框图
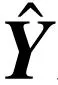
(1)
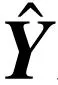
2.1逆量化算法


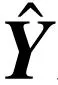
(2)
(3)
Δ为均匀量化步长.以b=2为例,当非关键帧观测值的两个最低有效位为10时,备选集由黑色区域组成,如图2所示.

图2 最低有效位为10时的备选集Ω示意图
Fig.2Schematic diagram of alternative setΩwhen the least bits is 10
2.2非关键帧观测值渐进量化的改进
经研究发现,渐进量化参数b的选取对逆量化质量有重大的影响.实验中通常把b设置得较大以获得较高的解码质量.但为了进一步降低码率,需要b尽可能小.

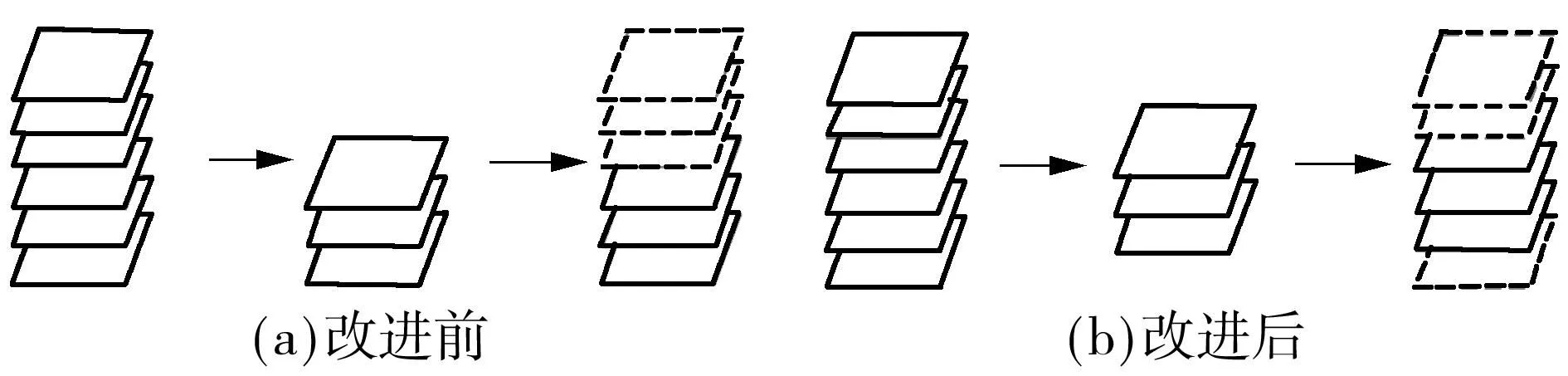
图3 非关键帧的渐进量化算法改进前后码平面传输比较
3仿真实验及结果分析
3.1性能分析
实验序列为30 Hz QCIF的Foreman,GOP长度为5,实验数据为一个GOP的结果.实验采用内插边信息生成方法[16],两级运动估计分别为初次估计和二次细化,运动估计示意图如图4所示,第1、第6帧为关键帧,第2至第5帧为非关键帧.图中的①、②、③为运动估计的先后顺序.

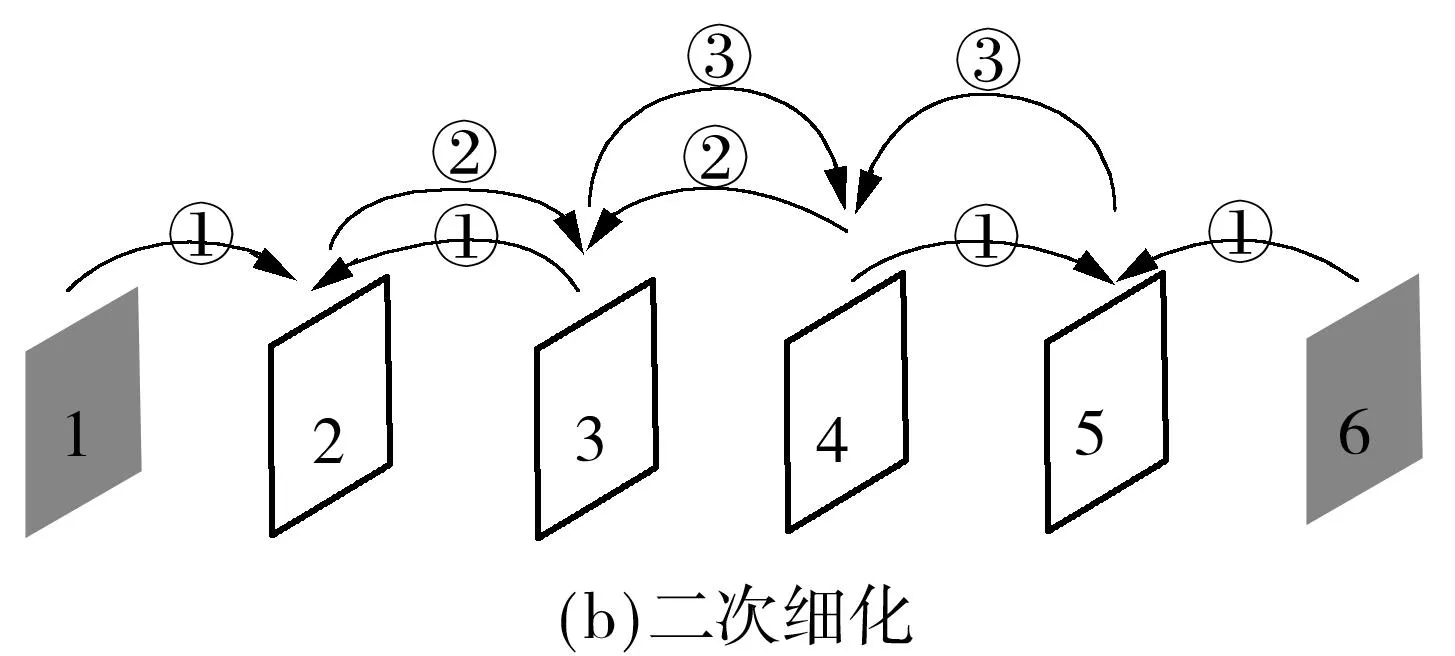
图4 GOP=5的运动估计示意图
在仿真实验中,分块大小为16×16,关键帧采样率为0.7,图像渐进量化[11]的量化参数B=7、b1=5.由于一个GOP的中间帧与关键帧的距离较大,边信息失真较严重,为了保证重构质量,该帧采样率比其他非关键帧的采样率稍高,文中选取为关键帧采样率的1/3(0.23),其余非关键帧采样率为0.005.原非关键帧渐进量化算法和文中改进的非关键帧渐进量化算法参数B=7;b=1,2,…,7.压缩感知重构算法为BCS-SPL-DDWT[17].仿真实验结果如图5所示,其中纵坐标为第90帧至第95帧的平均PSNR值.由实验结果可见,当1≤b≤5时,改进的渐进量化算法的重构质量明显优于原渐进量化算法.这表明非关键帧观测值的两个最重要码平面基本上能被正确恢复,较重要码平面所包含的正确信息对重构质量的贡献更大,因此传输相同数目的码平面时,改进的渐进量化算法能够获得更高的视频重构质量.
在相同码率下,改进的渐进量化算法在重构端能获得精度更高的观测值,从而获得更高质量的重构视频信号.
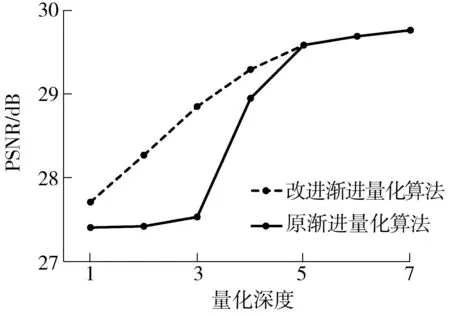
图5 两种渐进量化算法的性能比较
Fig.5Comparison of performance between two progressive quantization algorithms
3.2实验结果及分析
为验证文中所提算法的有效性,文中给出了30和15 Hz视频序列的实验结果,并与文献[15]的实验结果进行了比较.
3.2.130 Hz视频序列的实验结果
实验序列为30 Hz QCIF的Coastguard、Foreman和30 Hz CIF的News、Hall,实验数据为前150帧,GOP为5,运动估计方法与3.1节相同,QCIF和CIF视频序列的分块大小分别为16、32.
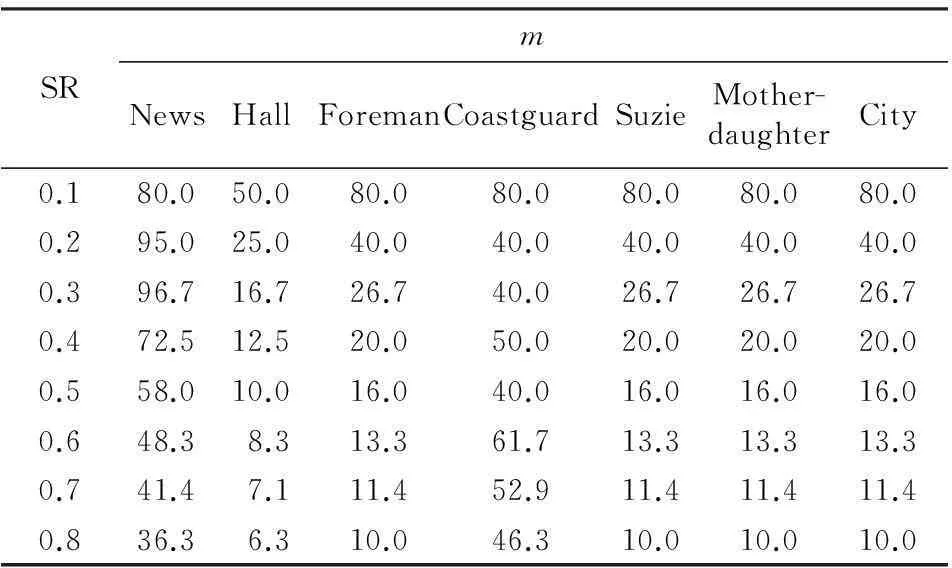
文中改进的渐进量化算法(VPQ)、均匀量化算法(SQ)及文献[15]量化算法的率失真(RD)性能曲线如图6所示.均匀量化算法的率失真性能是遍历多种采样率和量化深度选出的最优值,不同序列的均匀量化参数选取基本一致:采样率SR为0.1、0.2、0.3、0.4、0.5、0.6、0.7、0.8时,其量化深度B分别取为5、6、6、6、7、7、7、7.文中渐进量化算法的采样率和量化深度的选取与均匀量化算法一致,其率失真性能是在固定采样率SR和量化深度B下遍历b(非关键帧传输的码平面个数)的所有取值选出的最优值.实验中关键帧采样率为0.1~0.8,采用图像渐进量化[11]和帧内独立重构,b1=B-2;非关键帧采样率为0.005,GOP中间帧的采样率为关键帧采样率的1/3,采用非关键帧渐进量化和残差重构[17];所有帧重构算法为BCS-SPL-DDWT.经大量实验发现:B的选取与关键帧采样率有关,b的选取与非关键帧采样率有关,且B和b随采样率的降低而降低;m的选取与视频单帧复杂度有关,复杂度越高,最优的m越大.但目前还没有找到能准确选择最优参数的方法,实验中的量化参数都是基于遍历的最优经验值.不同采样率下各序列参数m的取值见表1.

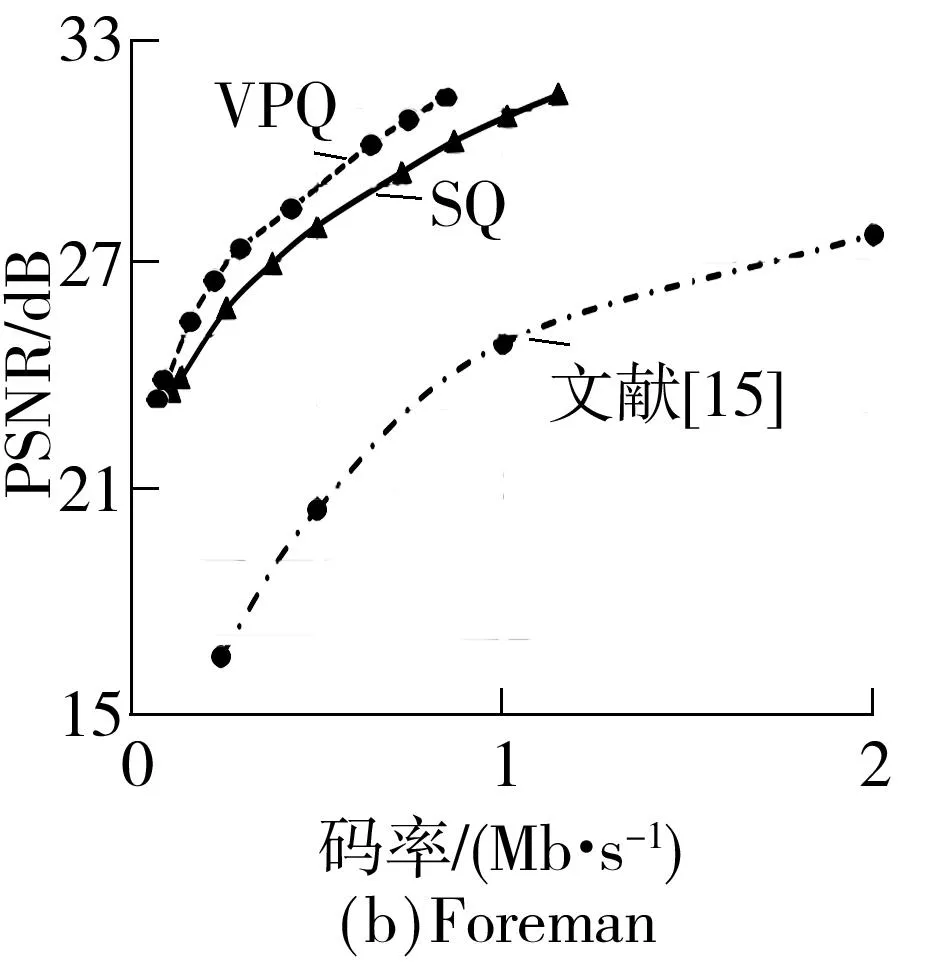
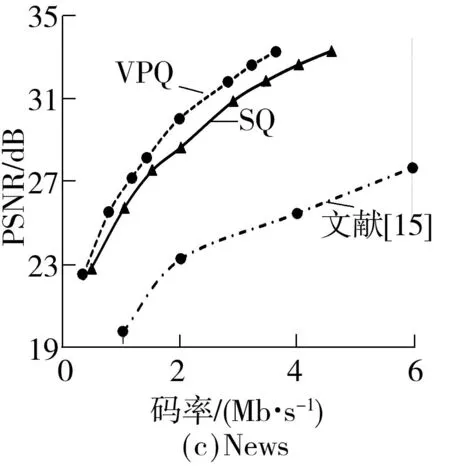
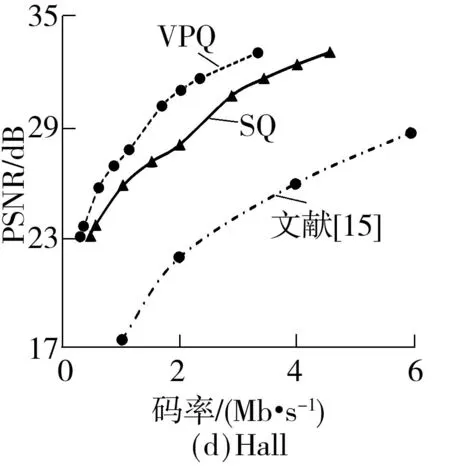
图6 3种算法对30 Hz序列的率失真性能比较
从图6可知:在相同码率下,文中算法对Coastguard、Foreman、News、Hall序列进行渐进量化并重构的PSNR值较文献[15]的实验结果分别提升了6.0、8.5、8.0、9.5 dB,这是因为文献[15]采用了残差量化的方法,在编码端观测完成后,关键帧独立量化,对非关键帧观测值与关键帧观测值之间的残差进行量化,传输量化符号,该方法虽然在一定程度上挖掘了帧间相关性,通过缩小量化范围来提升量化精度,但编解码的残差计算不太合理,从而导致了较大的误差累加,使得最终性能不佳;在相同码率下,文中算法对Coastguard、Foreman、News、Hall序列进行渐进量化并重构的PSNR值较均匀量化算法提升了1.5、1.0、1.0、2.0 dB,表明文中所提算法具有较优的率失真性能.这是因为文中算法在对观测值均匀量化后,只传输非关键帧观测值在重构端不能被准确估计的较重要码平面信息,在重构端利用视频帧间相关性,通过运动估计生成非关键帧的边信息,从而得到观测值的估计,并结合接收到的观测值信息精确地估计出缺失码平面,节省了重构端能准确估计的码平面所占用的资源,因此有效地降低了传输码率,取得较好的率失真性能.
表1不同采样率下各序列量化参数m的取值
Table 1Values of quantization parametermfor different sequences with different sampling rates
SRmNewsHallForemanCoastguardSuzieMother-daughterCity0.180.050.080.080.080.080.080.00.295.025.040.040.040.040.040.00.396.716.726.740.026.726.726.70.472.512.520.050.020.020.020.00.558.010.016.040.016.016.016.00.648.38.313.361.713.313.313.30.741.47.111.452.911.411.411.40.836.36.310.046.310.010.010.0
3.2.215 Hz视频序列的实验结果
与30 Hz的视频序列相比,15 Hz的视频序列帧间相关性减小,运动程度更为剧烈.为了进一步验证文中渐进量化算法的有效性,采用15 Hz QCIF的Suzie、Foreman、City、Mother-daughter序列的前150帧进行实验.Suzie及Mother-daughter序列的GOP=8,City及Foreman序列的GOP=4,其他条件均与3.2.1节实验相同.两种算法的率失真性能如图7所示.
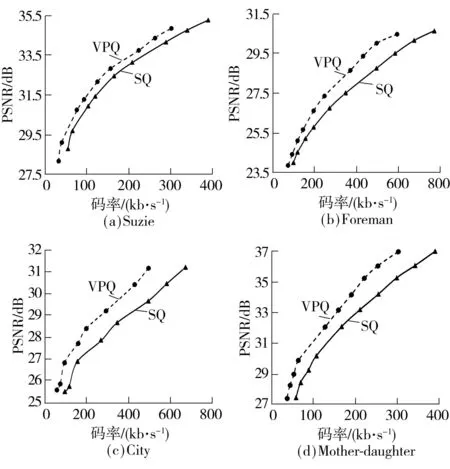
图7 两种量化算法对15 Hz序列的率失真性能比较
从图7可知,在相同码率下,文中算法对Suzie、Foreman、City、Mother-daughter序列进行渐进量化并重构的PSNR值较均匀量化算法分别提升了0.5、1.0、1.2、1.3 dB,具有较好的率失真性能.文中渐进量化算法能利用视频信号的时间相关性来降低码率,从而提升系统的整体率失真性能,且在视频序列帧间相关性不太强的情况下,文中算法的性能仍优于均匀量化算法.
为充分证明文中渐进量化算法的优越性,文中使用结构相似度(SSIM)来对重构视频序列的质量进行综合评测,两种算法重构Foreman和Mother-daughter序列的SSIM值如图8所示.从图中可知,在相同码率下,文中算法对Foreman、Mother-daughter序列进行渐进量化并重构的SSIM值较均匀量化算法分别提升了0.025、0.030,系统的率失真性能提升非常明显.

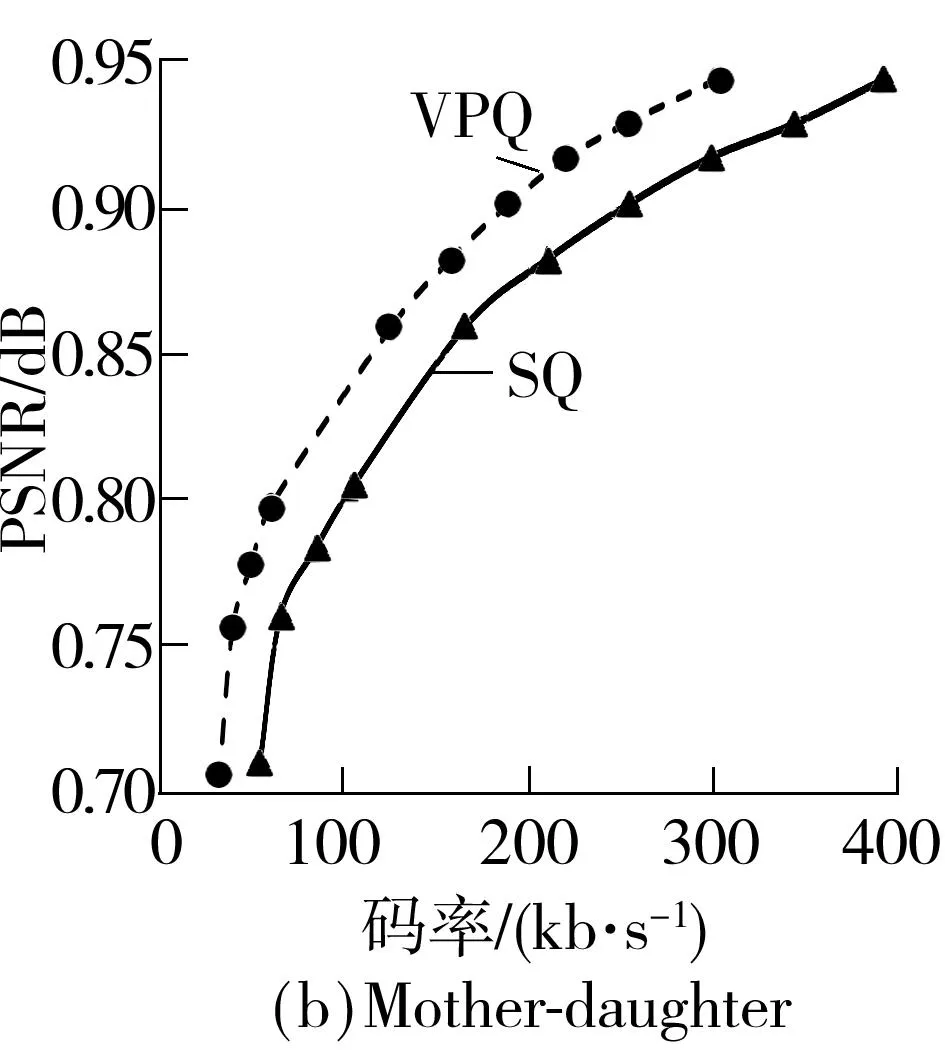
图8 两种算法对15 Hz序列的平均SSIM比较
Fig.8Comparison of average SSIM of different 15 Hz sequences between two quantization algorithms
Mother-daughter序列第82帧在均匀量化算法和文中渐进量化算法下的主观重构质量见图9,其中非关键帧采样率为0.005.由图9可见,两种算法对Mother-daughter序列第82帧(非关键帧)的重构质量基本一致,码率却大幅下降.这表明与均匀量化算法相比,文中算法能够大幅降低码率,且对最终重构质量不会产生太大的影响.
4结论
文中提出了基于视频信号帧间相关性和压缩感知的视频采集信号观测值渐进量化算法.该算法对非关键帧观测值均匀量化后只传输若干不太重要的码平面信息;在重构端利用邻近的已解码帧通过运动估计产生该非关键帧的边信息帧,再通过观测得到非关键帧观测值的估计,并结合接收到的不太重要码平面信息,通过渐进量化的逆量化得到精确的观测值.实验结果表明,在保持均匀量化复杂度和视频序列重构质量的基础上,文中算法能大幅降低码率,获得较高的率失真性能.由于基于压缩感知的视频采集信号观测值渐进量化的准确程度十分依赖于边信息帧的质量,因此文中算法暂不适用于运动程度较剧烈的场景.进一步改进渐进量化算法以适用于运动程度较剧烈的基于压缩感知的视频采集信号,以及寻找一个较优化的量化参数(B、b、m)的选取方法,是后续研究工作的重点.

图9 两种量化算法对Mother-daughter序列第82帧的主观重构质量比较
Fig.9Comparison of subjectively reconstructed quality of the 82nd frame in mother-daughter sequence between two quantization algorithms
参考文献:
[1]DONOHO D L.Compressed sensing [J].IEEE Transactions on Information Theory,2006,52(4):1289- 1306.
[2]CANDES E J,ROMBERG J,TAO T.Robust uncertainty principles:exact signal reconstruction from highly incomplete frequency information [J].IEEE Transactions on Information Theory,2006,52(2):489- 509.
[3]朱江,廖桂生,朱圣棋.基于块稀疏的空间碎片群目标成像方法 [J].电子与信息学报,2015(3):587- 593.ZHU Jiang,LIAO Gui-sheng,ZHU Sheng-qi.Space group debris imaging based on block-sparse method [J].Journal of Electronics & Information Technology,2015(3):587- 593.[4]常侃,覃团发,唐振华.基于联合总变分最小化的视频压缩感知重建算法 [J].电子学报,2014,42(12):2415- 2421.
CHANG Kan,QIN Tuan-fa,TANG Zhen-hua.Reconstruction algorithm for compressed sensing of video based on joint total variation minimazation [J].Acta Electronica Sinica,2014,42(12):2415- 2421.
[5]李然,干宗良,崔子冠,等.联合时空特征的视频分块压缩感知重构 [J].电子与信息学报,2014(2):285- 292.LI Ran,GAN Zong-liang,CUI Zi-guan,et al.Block compressed sensing reconstruction of video combined with temporal-spatial characteristics [J].Journal of Electronics and Information Technology,2014(2):285- 292.
[6]BOUFOUNOS P,BARANIUK R.Quantization of sparse representations [C]∥Proceedings of 2007 Data Compression Conference.Snowbird:IEEE,2007:378.[7]GOYAL V K,FLETCHER A K,RANGAN S.Compressive sampling and lossy compression [J].Signal Processing Magazine IEEE,2008,25(2):48- 56.
[8]CRAVEN D,MCGINLEY B,KILMARTIN L,et al.Effects of non-uniform quantization on ECG acquired using compressed sensing [C]∥Proceedings of 2014 EAI the 4th International Conference on Wireless Mobile Communication and Healthcare.Athens:IEEE,2014:79- 82.
[9]MUN S,FOWLER J E.DPCM for quantized block-based compressed sensing of images [C]∥Proceedings of the 20th European Signal Processing Conference.Bucharest:IEEE,2012:1424- 1428.
[10]QIAN C,ZHENG B,LIN B.Nonuniform quantization for block-based compressed sensing of images in differential pulse-code modulation framework [C]∥Proceedings of the 2nd International Conference on Systems and Informatics.Shanghai:IEEE,2014:791- 765.
[11]WANG L,WU X,SHI G.Binned progressive quantization for compressive sensing [J].IEEE Transactions on Image Processing,2012,21(6):2980- 2990.[12]SHIRAZINIA A,CHATTERJEE S,SKOGLUND M.Distri-buted quantization for compressed sensing [C]∥Procee-dings of IEEE International Conference on Acoustics,Speech & Signal Processing.Florence:IEEE,2014:6439- 6443.[13]BAIG Y,LAI E M K,LEWIS J P.Quantization effects on compressed sensing video [C]∥Proceedings of IEEE International Conference on Telecommunications.Doha:IEEE,2010:935- 940.
[14]LIU H,SONG B,TIAN F,et al.Joint sampling rate and bit-depth optimization in compressive video sampling [J].IEEE Transactions on Multimedia,2014,16(6):1549- 1562.
[15]MUN S,FOWLER J E.Residual reconstruction for block-based compressed sensing of video [C]∥Proceedings of 2011 Data Compression Conference.Snowbird:IEEE,2011:183- 192.[16]ASCENSO J,PEREIRA F.Hierarchical motion estimation for side information creation in Wyner-Ziv video coding [C]∥Proceedings of the 2nd International Conference on Ubiquitous Information Management and Communication.Suwon:ACM,2008:347- 352.[17]MUN S,FOWLER J E.Block compressed sensing of images using directional transforms [C]∥Proceedings of 2010 Data Compression Conference.Snowbird:IEEE,2010:547.
收稿日期:2015- 10- 19
*基金项目:国家自然科学基金资助项目(61471173);广东省自然科学基金资助项目(2016A030313455)
Foundation items: Supported by the National Natural Science Foundation of China(61471173) and the Natural Science Foundation of Guangdong Province(2016A030313455)
作者简介:杨春玲(1970-),女,博士,教授,主要从事图像/视频压缩研究、图像质量评价研究.E-mail:eeclyang@scut.edu.cn
文章编号:1000- 565X(2016)05- 0015- 07
中图分类号:TN 919.8
doi:10.3969/j.issn.1000-565X.2016.05.003
Progressive Quantization Algorithm for Video Signal Acquisition Based on Compressed Sensing
YANGChun-lingLIUXuan
(School of Electronic and Information Engineering,South China University of Technology,Guangzhou 510640,Guangdong,China)
Abstract:In the video signal acquisition process on the basis of compressed sensing,the quantization method of measured values influences the reconstructed quality remarkably.In order to design a high-performance quantization method of measured values,a progressive quantization algorithm for compressed video sensing measurements named VPQ (Video Progress Quantization) is proposed on the basis of the inter-frame correlation of videos and the characteristics of measured compressed video sensing signals.In this algorithm, the measured non-key frames are quantized and only some bitplanes with less importance are transmitted.At the decoder,neighbor reconstructed frames are applied to motion estimation to generate the side information of non-key frames,and then the non-key frame measurements are estimated by measuring the side information frame.Finally,in combination with the bitplanes with less importance transmitted from the encoder,accurate measurements are obtained via the inverse quantization of progressive quantization.Experimental results show that,in comparison with uniform scalar quantization,the proposed VPQ algorithm helps greatly decrease the code rate without additional complexity and reconstruction quality degradation;and that it is of higher rate-distortion performance,with a gain ranging from 0.5 to 2.0 dB for different sequences.
Key words:progressive quantization;compressed sensing;video coding

