基于阻抗匹配的IPT系统调谐电容特性*

孙跃　张静　叶兆虹　王智慧

(1.重庆大学 输配电装备及系统安全与新技术国家重点实验室, 重庆 400044; 2.重庆大学自动化学院, 重庆 400044)



基于阻抗匹配的IPT系统调谐电容特性*

孙跃1,2张静2叶兆虹2王智慧2

(1.重庆大学 输配电装备及系统安全与新技术国家重点实验室, 重庆 400044; 2.重庆大学自动化学院, 重庆 400044)

摘要:针对阻抗不匹配引起感应电能传输系统谐振频率不稳定的问题,提出了用于动态调谐的三电容组态阵列,分析了谐振电容与系统频率的关系以及电容阵列的容值分布、范围、输出精度,并采用遗传算法对三电容阵列的电容值进行优化.仿真实验结果表明,文中所提出的三电容阵列可获得较宽的输出电容范围及较高精度的可调电容值,适用于对输出电容值范围及可调精度要求较高的系统.

关键词：感应耦合电能传输;阻抗匹配;三电容阵列;电容值优化

感应电能传输(IPT)系统基于电磁感应原理,通过将原边回路的电能传送给副边回路的负载来实现无线电能传输[1- 8].无线电能传输技术具有安全、灵活、可靠等优点,已在交通、水下、矿井、医疗、厨房家电等领域得到广泛的应用,如在IPT系统通用能量供电平台实现了不同功率等级的家用电器的无线供电.

感应电能传输系统具有松耦合性质,当系统工作在高频时,会消耗大量的无功功率,通常采用电容补偿方式(即谐振电容储存的无功功率补偿谐振电感所需的无功功率)使系统工作在谐振状态.但在实际应用过程中,负载、传输距离、温度的变化或器件老化都将引起系统参数的变化,从而导致原边回路阻抗不匹配,使得系统频率失谐.因此,定值调谐电容已不能满足频率变化的要求,需要可变电容进行调节.

目前,可变电容的应用范围很广泛.当配电网中负荷电压波动较大时,需通过在配电网线路上串联可调电容来稳定负荷侧电压[9].在电气化铁道牵引供电系统中,负荷的动态变化也需要动态电容进行无功功率补偿[10].在感应电能传输领域,对动态电容的研究也有很多.文献[11]通过并联电容组构成可控电容阵列,但随着对电容值范围和可调精度要求的提高,并联电容组个数越多,其体积和控制难度越大.文献[12]提出了一种电容阵列,列举了可调电容的输出值,但没有对电容阵列的一般性应用进行分析.文献[13]提出了基于电容阵列的自适应阻抗匹配,但没有就电容阵列的电容值组合特性做具体说明.

针对以上问题,文中提出了三电容组态阵列,分析了可变电容的电容个数、输出电容值范围和精度,并采用遗传算法对可变电容模块的电容值进行优化,得到构成三电容阵列的电容取值;然后以谐振网络拓扑为原边电路串联、副边电路并联(SP)型的IPT系统为研究对象,根据系统负载的变化范围对三电容阵列的电容取值进行仿真分析,以验证其有效性.

1电路工作原理

IPT系统根据原、副边回路电容补偿方式的不同可分为4种最基本的谐振拓扑:SS、SP、PS、PP[14].文中以SP型拓扑结构为研究对象,SP型IPT系统的电路结构如图1所示,其中系统工作角频率为ω，Cp、Cs分别为原、副边谐振电感Lp、Ls的调谐电容,M为Lp、Ls之间的互感,Rp为原边耦合电感的内阻,RL为阻性负载.直流输入电压Edc通过逆变网络S1-S4产生高频方波电压源,经Lp、Cp串联谐振网络形成高频正弦交流电,其产生的磁链与副边线圈交链,从而在副边电路产生感应交变电动势,供给副边回路.

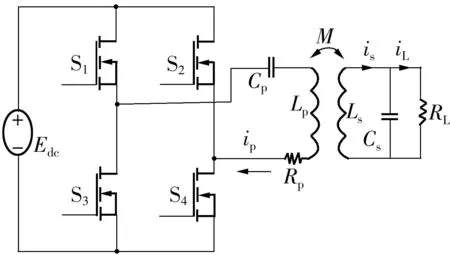
图1　SP型IPT系统的电路结构

由图1计算可知,副边电路总阻抗Zs为

(1)

基于交流阻抗法,副边等效到原边的反射阻抗Zr为

(2)

故原边系统总阻抗Zt为

(3)

由于系统工作在固有谐振点上,其原边总阻抗Zt的虚部为0,即Im(Zt)=0,由此可得到

(4)

由式(4)可知,原边调谐电容Cp与反射阻抗的虚部Im(Zr)(关于RL和M的函数)有关.负载的变化且使副边到原边的反射阻抗也发生变化,导致原边电路总阻抗不匹配(Im(Zt)≠0),从而引起系统谐振频率发生漂移.为保证系统工作频率不变,调谐电容Cp与负载RL变化的趋势如图2所示.因此,当负载RL发生变化时,定值调谐电容不能实现系统工作频率的稳定.

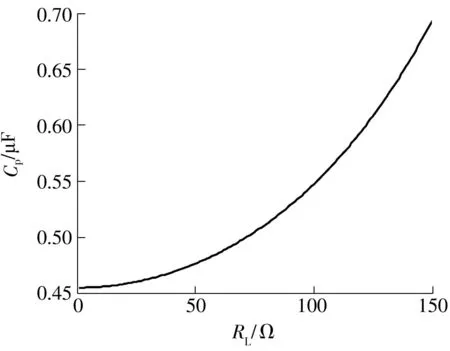
图2　原边谐振电容与负载的关系

综上所述,对于IPT系统因参数变化导致谐振频率发生漂移的问题,需要动态改变原边调谐电容值,以便在负载发生变化时能补偿原边回路阻抗,从而保证IPT系统的工作频率稳定.

2可变电容模块设计

为了保证IPT系统的工作频率与副边电路的固有频率保持一致,实现动态改变调谐电容,需要提供一个可变电容进行动态调谐.基于对可变电容的随机性和近似连续性的要求,可变电容应具有宽泛的容值范围以及较高的调节精度.因此,文中利用少量的定值电容,按照一定的组织结构和切换控制策略来设计能输出宽泛电容值范围和高精度电容值的可变电容模块.其中,电容个数、输出电容值的范围及精度是可变电容模块的评价标准.

假设可变电容模块中的N个电容的电容值分别为C1,C2,…,CN,输出等效电容值为Ceq.由于可变电容模块是通过切换控制方式实现若干标准电容的串并联组合来获得所需的等效电容值,因此输出等效电容值的最大值Ceq,max和最小值Ceq,min为

(5)

此外,离散程度可以反映可变电容模块的调节精度,文中根据输出等效电容值的范围和电容组合个数h来定义平均离散度θ:

(6)

电容个数为2、3、4时的可变电容模块参数如表1所示.

表1　可变电容模块参数

由表1可知,随着电容个数的增加,输出等效电容的最大值在逐渐增大,输出等效电容的最小值在逐渐减小,即输出等效电容值的范围越来越大,组合个数也越来越多.以IPT系统为例,设额定负载为50 Ω,在负载±100%的变化范围内,电容的变化范围在±15%左右,在输出电容值范围一定的情况下,随着电容个数的增加,其平均离散度越来越小.一般的工程要求误差控制在5%以内,而且在IPT系统稳态条件下,频率允许工作在ω1～ω2范围内,因此如果可变电容的输出电容值过于密集,则可能导致系统稳定时间过长或切换控制动作过于频繁.此外,在满足系统输出等效电容值范围和精度要求下,为了减小阵列的体积和控制难度,可变电容模块中的电容个数越少越好.而电容个数为3时是最简的形式,因此文中用3个标准容值电容器(C1、C2、C3)和6个开关器件(S1-S6)构成可变电容模块来实现输出电容值的变化,称为三电容模块,其结构如图3所示.

图3　可变电容模块结构

根据不同的切换控制,该三电容模块可输出17组等效电容值.

在实际应用中,为满足特殊工程性需要,在电容值范围要求大和调节精度高的情况下,可以将n个三电容模块并联,构成多模块可变电容阵列,如图4所示.

图4　多模块可变电容阵列结构

多个三电容模块并联,通过比例系数ki(i=1,2,…,n)连接,如C1i=kiC1,可提高输出电容值范围以及改善调节精度.

以两个三电容模块组成的阵列为例进行分析,在可变电容模块电容值C1、C2、C3以及模块间比例系数k确定后,该阵列与单模块的输出电容值范围对比如图5所示.

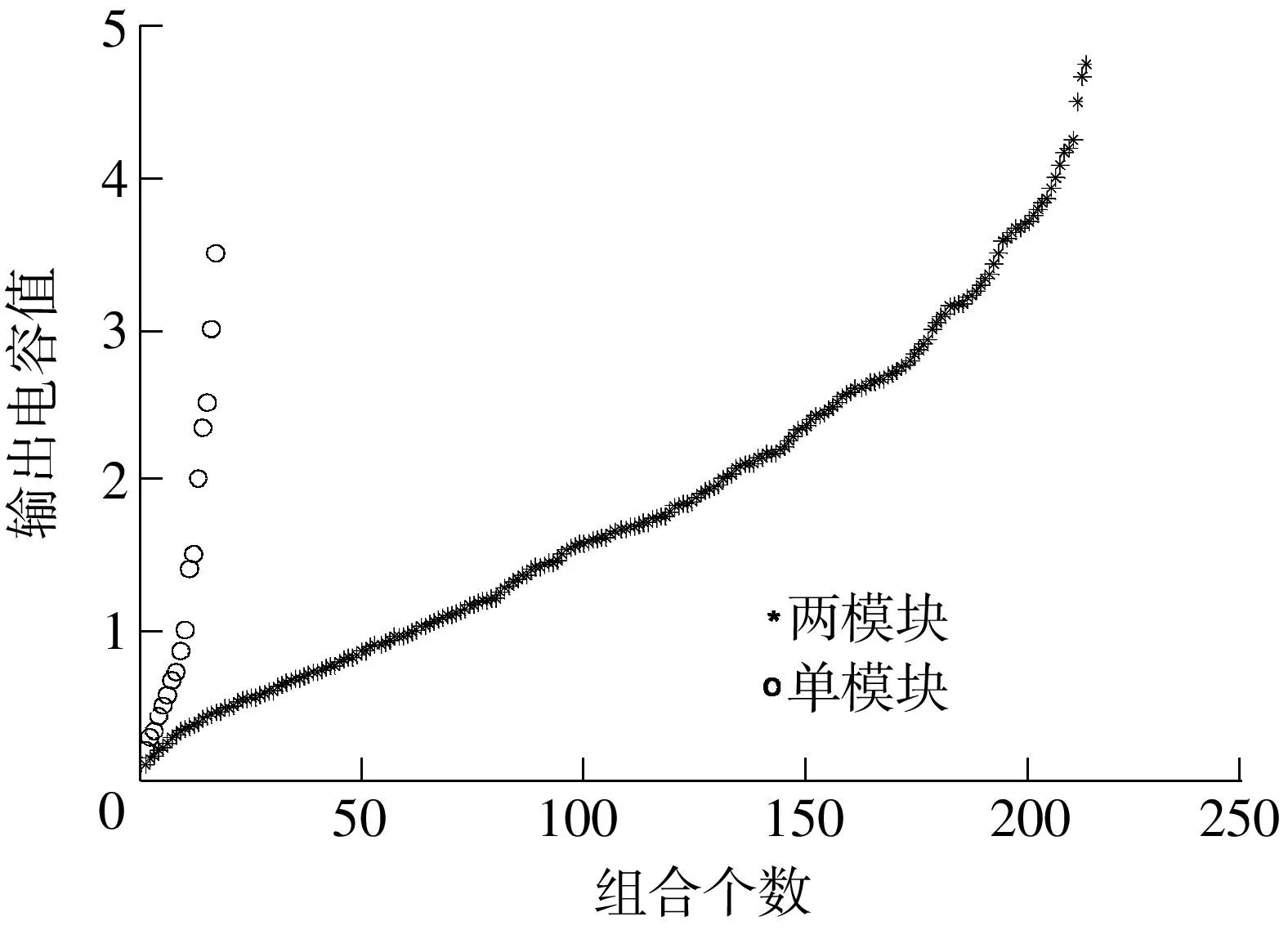
图5　单模块与两模块三电容阵列的输出电容值比较

Fig.5Comparison of output capacitance between one-module and two-module three-capacitor array

假设三电容模块的电容值C1、C2、C3分别取1.0、0.5、2.0,模块间比例系数k取0.5.两模块三电容阵列可以输出215个不同电容值.由图5可知,在输出电容值范围一致的情况下,两模块三电容阵列的平均离散度要明显小于单模块三电容阵列,且在输出电容值范围上也有明显的优势.因此,对输出电容值范围和精度要求很高的系统可以通过多模块连接来满足系统要求.

3三电容模块电容值的优化设计

为了使三电容模块能够更好地满足系统的要求,文中采用遗传算法对三电容模块的电容C1、C2、C3的取值进行优化设计,使得在三电容模块应用于不同功率等级系统时,都有与之对应的一组优化电容取值,从而满足输出等效电容值范围和调节精度的要求.

以期望电容值CR和三电容模块输出电容值Ceq的最小偏差作为目标函数,即

minZobj=Ceq-CR

(8)

同时将式(5)转换成不等式约束,期望等效电容值CR应包含在不等式内,即

Ceq,min≤CR≤Ceq,max

(9)

根据系统参数的变化范围推导出期望等效电容值CR的范围CR,min≤CR≤CR,max,结合式(5)、(9)得到关于三电容模块电容值C1、C2、C3的不等式约束,即

(10)

根据式(8)的目标函数和式(10)的变量约束,文中采用启发式遗传算法[15]来优化三电容模块的电容(C1、C2、C3)取值,具体步骤如下:首先采用二进制编码方法对各个变量进行编码,产生初始群体,将N个目标值Zobj按照由小到大的顺序排序,且分别赋予由大到小的适应度值;然后利用轮盘赌选择方法进行选择操作;最后以合适的概率对群体进行交叉及变异操作,得到优化的电容取值.

4优化及仿真验证

IPT系统已知条件为:负载变化范围为1～100 Ω,原边电感Lp=156 μH,拾取电感Ls=156 μH,互感M=51 μH,原边调谐电容Cp=0.47 μF,副边调谐电容Cs=0.43 μF.由此可知该系统的期望电容值变化范围为0.45～0.54 μF.采用遗传算法对三电容模块电容取值C1、C2、C3进行优化,结果如图6所示.

图6　遗传算法的优化结果

由图6可知,遗传算法经过70代迭代后收敛,得到的电容取值为C1=0.481 μF、C2=0.051 μF、C3=0.458 μF.通过切换控制方式得到三电容模块的输出电容值Ceq与期望电容值CR的比较结果,如图7(a)所示.

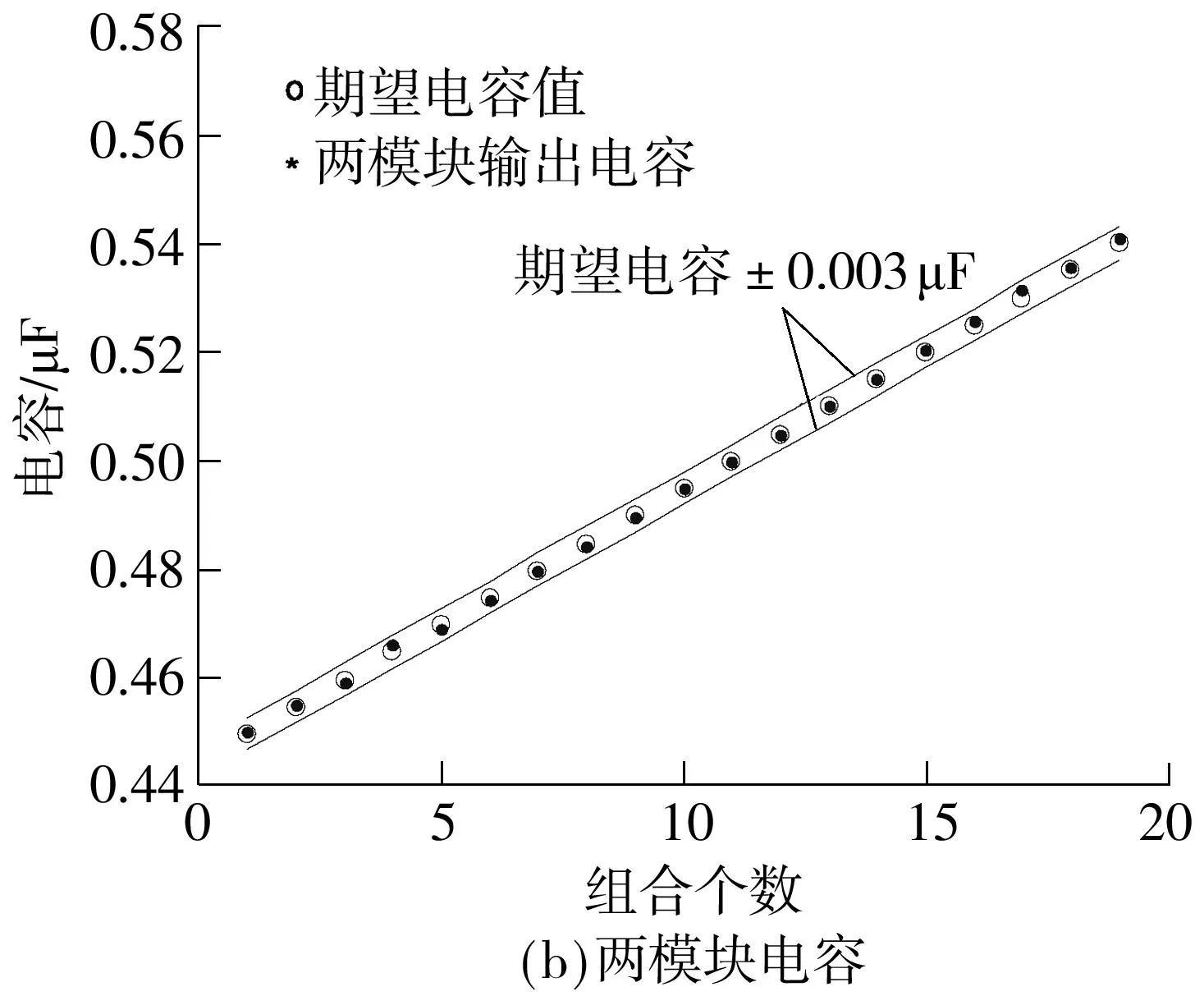
图7　单模块与两模块三电容阵列的Ceq与CR比较

Fig.7Comparison betweenCeqandCRfor one-module and two-module three-capacitor array

由图7(a)可知,经遗传算法优化得到的三电容模块的电容取值(C1、C2、C3),在验证过程中以期望电容值为基准,可变电容的输出电容值与期望等效电容值的误差基本上控制在±0.01 μF以内,因此采用遗传算法对三电容模块的电容取值进行优化,可以取得很好的效果,这也说明了三电容模块能够满足系统的输出电容值范围及调节精度要求.

此外,将两模块三电容阵列输出电容值与上述期望电容值进行对比,采用遗传算法得到其电容取值为C1=0.388 μF、C2=0.100 μF、C3=0.361 μF、k=0.153,最后输出的电容值与期望电容值的比较如图7(b)所示.由图7(b)可知,两模块三电容阵列的输出电容值与期望电容值误差很小,仅在±0.003 μF以内.另外,两模块三电容阵列可输出323个不同的电容值,扩大了输出电容值范围且提高了可调精度,从而说明了三电容阵列可适用于对输出电容值范围及可调精度要求更高的系统.

5结论

为了实现对工作频率稳定的控制,文中提出了三电容阵列,分析了可变电容的输出电容值范围、精度以及电容个数,同时采用遗传算法对电容阵列电容取值进行优化,得到优化的电容取值,并通过仿真验证了三电容阵列的有效性.本研究对可变电容的研究有一定的参考价值,对三电容阵列的切换控制是今后的研究内容.

参考文献：

[1]SALLAN J,VILLA J L,LLOMBART A,et al.Optimal design of ICPT systems applied to electric vehicle battery charge [J].IEEE Transactions on Industrial Electronics,2009,56(6):2140- 2149.

[2]HU A P,HUSSMANN S.Improved power flow control for contactless moving sensor applications [J].IEEE Power Electronics Letters,2004,2(4):135- 138.

[4]HSU J U W,HU A P,SWAIN A.A wireless power pickup based on directional tuning control of magnetic amplifier [J].IEEE Transactions on Industrial Electronics,2009,56(7):2771- 2781.

[5]SI P,HU A P,MALPAS S,et al.A frequency control method for regulating wireless power to implantable devices [J].IEEE Transactions on Biomedical Circuits and Systems,2008,2(1):22- 29.[6]张波,张青.两个负载接收线圈的谐振耦合无线输电系统特性分析 [J].华南理工大学学报(自然科学版),2012,40(10):152- 158.

ZHANG Bo,ZHANG Qing.Characteristic analysis of magnetic resonant coupling-base wireless power transfer system with two receivers [J].Journal of South China University of Technology(Natural Science Edition),2012,40(10):152- 158.

[7]孙跃,夏晨阳,苏玉刚,等.导轨式非接触电能传输系统功率和效率的分析与优化 [J].华南理工大学学报(自然科学版),2010,38(10):123- 129.

SUN Yue,XIA Chen-yang,SU Yu-gang,et al.Analysis and optimization of transmission power and efficiency for rail-type contactless power transfer system [J].Journal of South China University of Technology(Natural Science Edition),2010,38(10):123- 129.

[8]范兴明,莫小勇,张鑫.无线电能传输技术的研究现状与应用 [J].中国电机工程学报,2015,35(10):2584- 2600.FAN Xing-ming,MO Xiao-yong,ZHANG Xin.Research status and application of wireless power transmission technology [J].Proceeding of the CSEE,2015,35(10):2584- 2600.

[9]张先泰,蔡金锭,丁智华,等.电容补偿在配电网电压调节中的应用 [J].电力自动化设备,2011,31(2):116- 118.

ZHANG Xian-tai,CAI Jin-ding,DING Zhi-hua,et al.Application of capacitance compensation in voltage adjustment of distribution power system [J].Electric Power Automation Equipment,2011,31(2):116- 118.

[10]贺建闽,黄治清,李群湛.牵引变电所固定并联电容补偿有效性评价 [J].铁道学报,2004,26(3):41- 45.

HE Jian-min,HUANG Zhi-qing,LI Qun-zhan.Evaluation of the effectiveness of the fixed parallel capacitor compensation used in traction substation [J].Journal of the China Railway Society,2004,26(3):41- 45.

[11]孙跃,吴静,王智慧,等.ICPT系统基于电容阵列的稳频控制策略 [J].电子科技大学学报,2014,43(1):54- 59.SUN Yue,WU Jing,WANG Zhi-hui,et al.Frequency stabilization control method for ICPT system based on capacitor array [J].Journal of University of Electronic Science and Technology of China,2014,43(1):54- 59.

[12]戴欣,周继昆,孙跃.基于谐振电容阵列的CPT系统输出控制方法 [J].电子科技大学学报,2012,41(5):729- 734.

DAI Xin,ZHOU Ji-kun,SUN Yue.Study on output vol-tage stability of CPT system based on resonant capacitor array [J].Journal of University of Electronic Science and Technology of China,2012,41(5):729- 734.

[13]LIM Y,TANG H,LIM S,et al.An adaptive impedance-matching network based on a novel capacitor matrix for wireless power transfer [J].IEEE Transactions on Power Electronics,2014,29(8):4403- 4413.

[14]WANG C S,COVIC G A,STIELAU O H.Power transfer capability and bifurcation phenomena of loosely coupled inductive power transfer systems [J].IEEE Transactions on Industrial Electronics,2004,51(1):148- 157.[15]张治国,谢运祥,袁兆梅.高功率因数LCC谐振电路的多目标优化 [J].华南理工大学学报(自然科学版),2012,40(11):94- 100.ZHANG Zhi-guo,XIE Yun-xiang,YUAN Zhao-mei.Multi-objective optimization of LCC resonant circuit with high power factor[J].Journal of South China University of Technology(Natural Science Edition),2012,40(11):94- 100.

收稿日期:2015- 09- 11

*基金项目:国家自然科学基金资助项目(51277192);国家“863”计划项目(2015AA010402)

Foundation items: Supported by the National Natural Science Foundation of China(51277192) and the National High-Tech R & D Program of China(2015AA010402)

作者简介:孙跃(1960-),男,教授,博士生导师,主要从事电力电子技术及其应用、感应耦合电能传输技术研究.E-mail:syue06@cqu.edu.cn

文章编号:1000- 565X(2016)05- 0042- 06

中图分类号：TM 131

doi：10.3969/j.issn.1000-565X.2016.05.007

Characteristic of Tuned Capacitor in IPT System Based on Impedance Matching

SUNYue1,2ZHANGJing2YEZhao-hong2WANGZhi-hui2

(1.State Key Laboratory of Power Transmission Equipment and System Security and New Technology,Chongqing University,Chongqing 400044,China;2.School of Automation,Chongqing University,Chongqing 400044,China)

Abstract:In order to overcome the instable resonance frequency of inductive power transmission system caused by impedance mismatch,a three-capacitor configuration array for dynamic tuning is proposed,and the relationship between resonant capacitance and system frequency is analyzed. Moreover,the value distribution, scope and output precision of capacitor array are discussed,and the capacitance value of the three-capacitor array is optimized by means of genetic algorithm.Simulated results indicate that,as the proposed three-capacitor array presents wide-scope output capacitance and high-precision adjustable capacitance,it can be applied to the system that requires large output capacitance range and high adjustable precision.

Key words:inductive coupling power transmission;impedance matching;three-capacitor array;capacitance optimization