盾构隧道管片弯矩分布特性数值模拟分析

李守巨,李　浩，上官子昌

(1. 大连理工大学工业装备结构分析国家重点实验室，辽宁　大连　116024；2. 大连海洋大学海洋与土木工程学院，辽宁　大连　116204)



盾构隧道管片弯矩分布特性数值模拟分析

李守巨1,李浩1，上官子昌2

(1. 大连理工大学工业装备结构分析国家重点实验室，辽宁大连116024；2. 大连海洋大学海洋与土木工程学院，辽宁大连116204)

摘要：为了研究盾构隧道衬砌内力分布规律，对盾构隧道设计中常用的三种衬砌内力计算方法进行了归纳和分析。基于土力学理论土压力的计算方法，提出了计算管片内力分布新的荷载-结构模型。以沈阳地铁盾构隧道为例，比较分析了惯用法、有限元法以及荷载-结构计算方法的区别。计算结果表明，不同的计算方法得到的弯矩分布特性存在一定的差异。采用有限元数值模拟方法，分析了土体泊松比对盾构隧道管片弯矩的影响。研究表明，随着土体泊松比的增加，管片最大弯矩值减小。

关键词：盾构隧道管片；土压力；土力学；弯矩；土体泊松比

近年来，世界上隧道工程的大量建设极大促进了隧道工程相关技术水平的进步，大多数国家在盾构隧道衬砌结构的设计方面都已形成较为固定的方法。但是，对于不同土层条件下计算模型以及荷载计算方法的选用并没有明确的规定，使得各种数值计算方法在隧道及地下工程中涌现出来，这对大量的设计和施工起到了良好的指导作用。

目前根据我国地下结构设计的特点，隧道结构设计分为四种：经验类比模型；荷载结构模型[1]；地层结构模型[2]；收敛约束模型[3]。假设地层对管片的作用只是产生作用在地下管片结构上的荷载，以计算管片在荷载作用下产生的内力和变形的方法称为荷载结构法；假设管片与地层一起构成受力变形的整体，并可按连续介质力学原理计算衬砌和周边地层的计算方法称为地层结构法[4]。收敛约束模型则是以测试为主的设计方法，但收敛约束法的原理还不完善，存在很多问题难以解决，使得该方法仍只能停留在定性的描述阶段。

实际上，在隧道工程结构设计中，由于地下结构的设计受到各种复杂因素的影响[5]，而这些因素的影响规律还没有完全被人们所完全认识，使得理论计算的结果常与工程实际有较大的差异，很难用作实际的设计依据[6]。即使内力分析采用了比较严密的理论推导，其计算结果往往也需要用经验类比来加以判断和补充，因此隧道设计仍难摆脱经验方法的约束，经验方法在我国隧道设计中仍占主导地位。尽管信息化设计作为隧道工程设计理论的一个方向，但在其预设计阶段，支护参数仍须采用经验方法来确定。同时由于经验方法的理论及数据限制，基于经验和科学建立起来的隧道工程设计模型，其设计水平的提高，最终仍将依赖理论上的发展与突破。目前，基于有限元数值模拟方法越来越广泛的应用于盾构隧道的研究。文献[7]通过三维模拟对盾构隧道施工的机械行为进行了有限元分析； 文献[8]利用数值模拟分析了灌浆压力和工作面推力对引起的地面沉降的影响； 文献[9]利用梁单元模拟衬砌结构， 弹簧单元模拟围岩抗力， 点弹簧单元模拟墙角支座通过有限元法计算衬砌的内力和变形； 文献[10]通过一系列有限元方法分析了不同环境下隧道表面的沉降情况； 文献[11]采用FLAC3D有限差分程序对双隧道施工过程的影响因素进行了数值统计与分析。

通过模拟某盾构掘进的隧道，在忽略管片接头的基础上，即将管片视为抗弯刚度均匀的圆环，采用惯用设计法[12]，有限元法[13]和荷载-结构计算方法，得到隧道管片的弯矩分布，模拟计算了土体泊松比对隧道管片弯矩的影响。

1盾构隧道管片计算模型与方法

据统计，隧道建设费用中衬砌费用往往占整个隧道工程造价的30%～40%，因此，隧道衬砌结构设计必须安全可靠，同时经济合理。基于经典的管片内力计算方法惯用设计法以及有限元法，本文提出了新的计算模型，荷载-结构法。

1.1管片内力计算的惯用设计法

日本规范的隧道管片弯矩分布计算方法即为惯用设计法，其在计算过程中假设管片环是弯曲刚度均匀的圆环，它不考虑接头所引起的管片环局部刚度降低。在设计中，考虑了隧道顶部与底部的均布线荷载，隧道侧面的线性分布荷载，管片的自重以及水平方向地层抗力。

惯用法所使用的荷载体系如图1所示，垂直方向的地层抗力为等分布荷载，水平方向的地层抗力假定为管片环顶部开始左右45°～135°线性分布荷载(三角形分布)。则任意截面的弯矩值为垂直荷载、水平荷载、水平三角荷载、地层抗力以及自重产生的弯矩值之和。

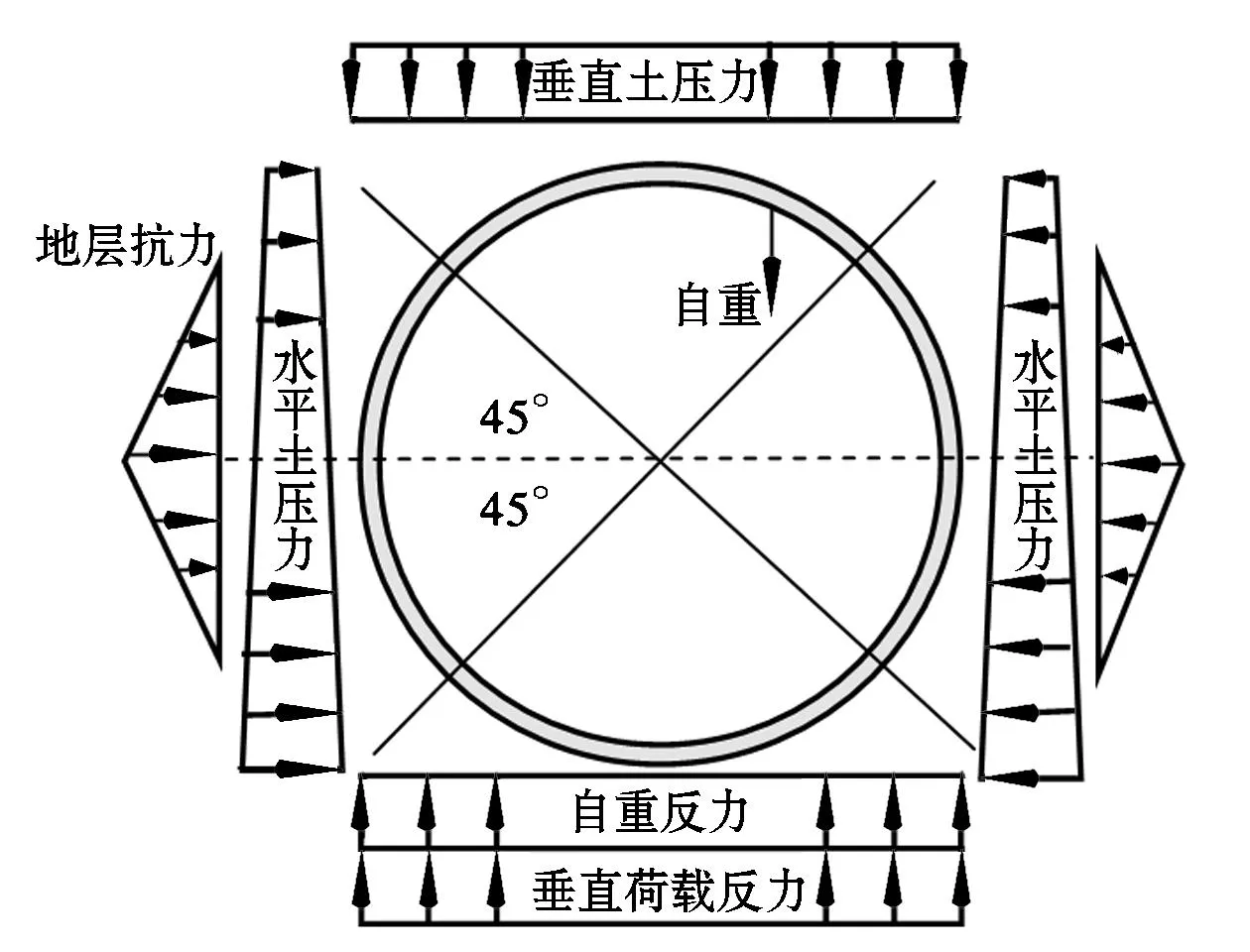
图1　惯用法计算模型

1.2管片内力计算的有限元数值方法

由于隧道结构是在地层中修建的，其工程特性、设计原则及方法与地面结构不同，隧道结构的变形受到周围土体本身的约束，从某种意义上讲，土体也是地下结构的荷载，同时也是结构本身的一部分。

根据局部变形理论，隧道管片结构弯矩分析可以简化为内力计算力学模型(见图2)， 并通过ANSYS软件实现平面内弯矩的计算。 假设管片圆环是弯曲刚度均匀的如图2所示的位于土体中心的圆环， 选用ANSYS单元库里的梁单元BEAM3来模拟管片。 同时假设管片四周的土体为均匀的弹性变形体， 选用平面实体单元PLAN42模拟土体。 土体两侧施加水平位移约束，土体底部施加垂直位移约束。

图2　有限元法计算模型

1.3管片内力计算的荷载-结构法

荷载-结构法是将支护结构和围岩分开来考虑，这种模型认为隧道支护结构与围岩的相互作用是通过弹性支撑对结构施加约束来体现的[14]，而土体承载能力则在确定土体压力与弹性支撑的约束能力时直接地考虑。支护结构是承载主体，土体作为荷载的来源和支护结构的弹性支撑，并等效为作用于支护结构单元节点上的径向和切向荷载。在大多数情况下，切向荷载比径向荷载小，为简化而忽略其作用，仅对支护结构离散单元进行分析。

取四分之一管片作为简化模型(见图3)，选用平面单元PLAN42模拟管片圆弧，模型顶端施加水平位移约束，底部施加垂直位移约束，管片圆弧外侧施加法向荷载。利用这种模型进行隧道设计的关键是如何确定作用在支护结构上的主动荷载。

图3　荷载-结构法计算模型

已知基于弹性力学理论得到的任意深埋条件下的垂直土压力为

pv=∑ρighi

(1)

式中：Pv为垂直土压力；ρ为土体密度；g为重力加速度；h为埋深；i为土层编号。

根据弹性力学理论，其水平土压力为

(2)

(3)

式中：Ph为水平土压力；μ为土体的泊松；λ为侧向土压力系数。

基于土力学理论得到侧压力系数

(4)

则ph=(1-sinφ)pv

(5)

作用在管片的法向压力为

P=Pvcos2θ+Phsin2θ

(6)

(7)

式(4～7)中：φ为土体的内摩擦角；P为施加在管片外侧的法向压力；θ为管片模型任意截面与y轴正向的夹角；x，y分别为管片模型外侧面任意点的横坐标和纵坐标。

2管片内力计算的数值算例分析

以沈阳地铁云峰北街——沈阳站的地质条件为例，选取一种简单的地质模型进行对比分析(见图4)。隧道管片位于某均质单一土层，隧道覆土厚度15 m，土体容重18 kN/m3，弹性模量40 MPa，泊松比0.33，内摩擦角30°，地基抗力系数30 MN/m3。混凝土管片外径6 m，管片厚度350 mm，容重24 kN/m3，弹性模量34.5 GPa，泊松比0.20。

图4　盾构隧道管片算例模型

由式(3)和式(4)两种方法计算得到土层的侧向土压力系数值均为0.5。分别采用以上提出的三种计算方法，得到隧道管片四分之一圆环在侧向土压力系数同为0.5的情况下的弯矩值随角度变化(见图5)。

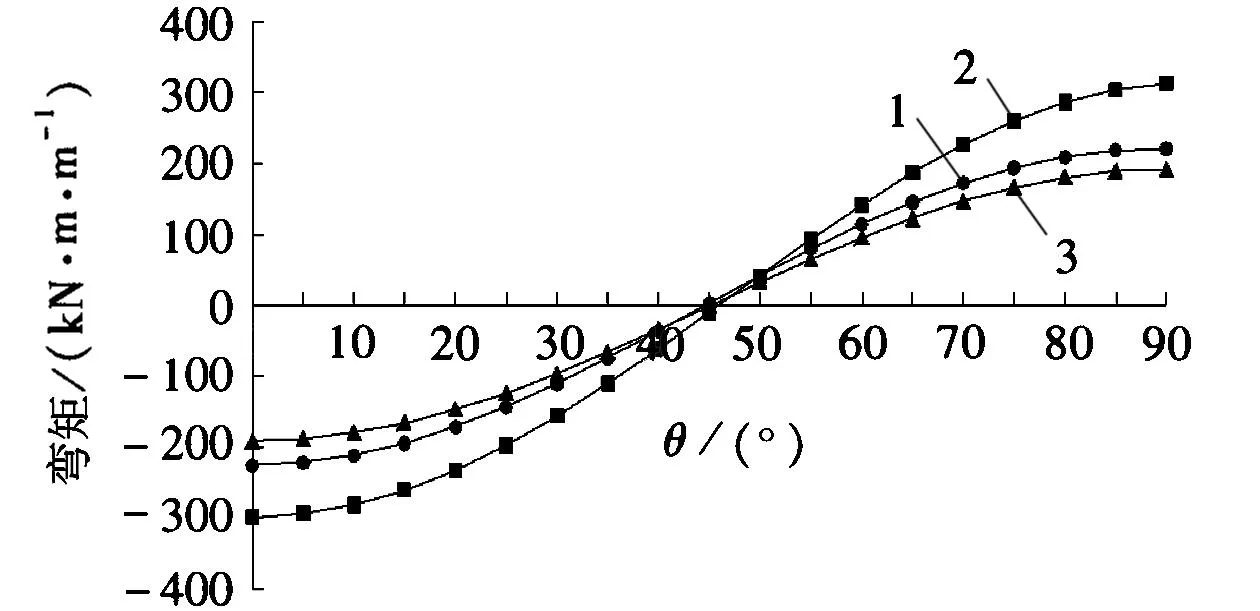
1. 惯用法；2. 有限元法；3. 荷载-结构法图5　不同方法管片的弯矩图对比

基于有限元的隧道管片弯矩分布计算方法中，选用BEAM3单元模拟隧道管片，通过改变土体的泊松比μ，得到不同泊松比时的弯矩(见图6)。

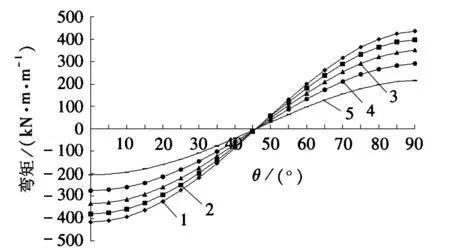
1. μ=0.2；2. μ=0.25；3. μ=0.3；4. μ=0.35；5. μ=0.4图6　不同泊松比管片的弯矩分布

由图6可得到管片不同泊松比的最大弯矩值变化情况(见图7)，通过拟合该曲线可得到管片的最大弯矩值Mmax(kN·m/m)同泊松比μ之间的关系式

Mmax=-1 106.15μ+658.31

(9)

μ图7　不同泊松比管片的最大弯矩值

土体泊松比为0.33时隧道管片的弯矩分布如图8所示，弯矩的正负号规定为：使衬砌内弧面受压为正，内弧面受拉为负，单位kN·m/m。通过图8可以看出，管片腰部受压弯矩最大，管片顶部及底部受拉弯矩最大。

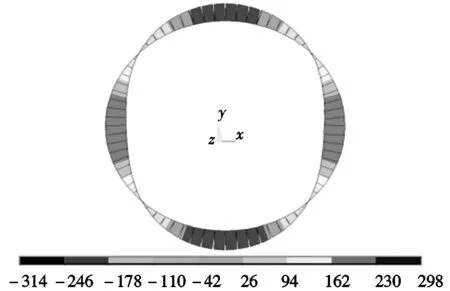
弯矩/(kN·m·m-1)图8　有限元模拟泊松比0.33时管片弯矩分布

土体泊松比为0.33时隧道管片的轴力分布如图9所示，轴力的正负号规定为：压缩为负，拉伸为正，单位kN/m。

轴力/(kN·m-1)图9　有限元模拟泊松比0.33时管片轴力分布

通过图9可以看出，管片整体受到压缩轴力作用，其中顶部轴力值最小，腰部轴力值最大。

3结论

1) 当土体泊松比为0.33时，根据弹性力学理论得到土体的侧向土压力系数为0.5。当土体的内摩擦角为30°时，根据土力学理论得到土体的侧向压力系数也为0.5。荷载-结构法与日本惯用设计法所得到的管片最大弯矩值比较接近，有限元法得到的管片最大弯矩值偏大。

2) 三种方法得到的隧道管片弯矩分布形状基本一致，即在土压力作用下四分之一隧道管片在0°和90°弯矩值最大但方向相反。在45°附近弯矩值为0，其他四分之三管片圆环弯矩分布与垂直轴呈对称形状。

3) 有限元模拟结果表明土体的泊松比影响隧道管片弯矩值，隧道管片的弯矩值随土体泊松比增大而减小，但不影响隧道管片的弯矩分布形状。

参考文献：

[1]曾东洋， 何川. 盾构隧道衬砌结构内力计算方法的对比分析研究[J].地下空间与工程学报， 2005，1(5)：707-712.

[2]张京，胡鹏，李国峰. 城市隧道结构设计研究[J].地下空间与工程学报，2014， 10(S1)：1 679-1 745.

[3]武振国， 常翔， 叶飞. 盾构隧道结构设计模型综述[J].隧道建设， 2008， 28(2)：182-185.

[4]高云龙， 郭小红. 盾构隧道非均质等效梁模型的建立与分析[J]. 铁道学报， 2013， 35(7)：123-128.

[5]ZHU J F， XU R Q， LIU G B. Analytical prediction for tunnelling-induced ground movements in sands considering disturbance[J]. Tunnellingand Underground Space Technology， 2014， 41(1)：165-175.

[6]THOMAS K， GUNTHER M. A numerical study of the effect of soil and grout material properties and cover depth in shield tunnelling[J]. Computers and Geotechnics，2006， 33(4-5)：234-247.

[7]陈俊生，莫海鸿.盾构隧道管片施工阶段力学行为的三维有限元分析[J].岩石力学与工程学报， 2006，25(S2)：3 482-3 489.

[8]王非，缪林昌，黎春林. 考虑施工过程的盾构隧道沉降数值分析[J].岩石力学与工程学报， 2013，32(S1)：2 907-2 914.

[9]周宪伟，赵新江，李宏宇.公路隧道衬砌有限元分析[J]. 黑龙江工程学院学报，2014， 28(5)：20-23.

[10]KARAKUS M， FOWELL R J. Effects of different tunnel face advance excavation on the settlement by FEM[J]. Tunnelling and Underground Space Technology， 2003，18(5)：513-523.

[11]DO N， DIAS D， ORESTE P，et al. Three-dimensional numerical simulation of a mechanized twin tunnels in soft ground[J]. Tunnelling and Underground Space Technology， 2014， 42(5)：40-51.

[12]侯公羽， 杨悦， 刘波. 盾构管片设计改进惯用法模型及其内力解析解[J]. 岩土力学， 2008，29(1)：161-166.

[13]陈卫星. 盾构管片均质圆环法计算模型探讨[J]. 有色冶金设计与研究，2011， 32(S1)：39-42.

[14]上官子昌，李守巨，孙伟，等.盾构机掘进工作面土压力计算方法比较分析[J].哈尔滨工业大学学报，2011，43(S1)：111-114.

(责任编辑：何学华，吴晓红)

Numerical Simulation Analysis of Bending Moment Distribution Characteristics in Shield Tunnel Segment

LI Shou-ju1，LI Hao1，SHANGGUAN Zi-chang2

( 1. State Key Laboratory of Structural Analysis for Industrial Equipment, Dalian University of Technology, Dalian Liaoning 116024, China; 2. Institute of Marine and Civil Engineering, Dalian Ocean University, Dalian Liaoning 116204, China)

Abstract:In order to study the distribution of internal force of shield tunnel lining, three kinds of computational procedures for calculating bending moment distribution in segments of shield tunnel were summarized and analyzed. A new loading-structure method for calculating the distribution characteristics of bending moment was proposed based on soil pressure calculation method with the soil mechanics principles. Taking the shield tunnel in Shenyang Metro as an example, the difference of bending moment distribution calculated with the common method, finite element method and loading-structure method were compared. The computational results showed that there are some differences for bending moment distribution calculated with different computational methods. By using finite element method, the influence of the coefficient of earth pressure at-rest on bending moment distributions was simulated. The results showed that the maximum moment on segment decreases with increase of the coefficient of earth pressure at-rest.

Key words:shield tunnel segment; earth pressure; earth mechanics; bending moment; Poisson's ratio of soil

收稿日期：2015-04-10

基金项目：国家重点基础研究发展计划资助项目(2015CB057804)；国家自然科学基金资助项目(51105048, 51209028)；工业装备结构分析国家重点实验室开放基金资助项目(S14206)

作者简介：李守巨(1960-)，男，辽宁沈阳人，教授，博士，研究方向：岩石力学和混凝土结构的参数反演研究。

中图分类号：U459.3

文献标志码：A

文章编号：1672-1098(2016)01-0001-05