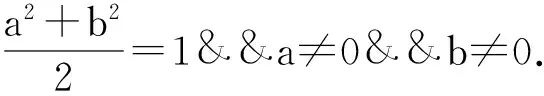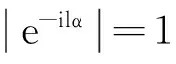一种改进的图像表示算法

孙克争　汤丽娟,2

(1.江苏商贸职业学院　江苏南通　226011； 2.中国矿业大学信息与电气学院　江苏徐州　221116)



一种改进的图像表示算法

孙克争1汤丽娟1,2

(1.江苏商贸职业学院江苏南通226011； 2.中国矿业大学信息与电气学院江苏徐州221116)

摘要：自从极谐波变换(Polar Harmonic Transforms，PHTs)提出后，因其内核计算简单，被广泛用于图像分析和模式识别，而PHTs在高阶时表现出不稳定性，极谐波复指数变换(PCET)在低阶时就有可能表现出不稳定性。为了设计出可以广泛应用于图像表示的矩，提出一种使用新的径向内核函数的极谐波正—余弦变换(Polar Cosine-Sine Transform, PCST)来实现可靠的稳定性。实验结果表明，采用该算法进行图像表示时的稳定性明显优于PHTs，尤其在高阶矩时仍能够保持数值稳定性，同时具有旋转不变性。

关键词：极谐波变换； 旋转不变性； 极谐波正—余弦变换

近年来，学者们提出了多种矩变换和旋转不变矩。例如，Zernike矩[1]，伪Zernike矩[2]，正交Fourier-Mellin矩[3]，Jacobi-Fourier矩[4]等，这些都是基于Jacobi多项式径向内核的方法。由于径向内核的计算涉及复杂的阶乘计算，时间长，因此限制了应用范围。2010年，Pew-Thian Yap等提出了一种改进的二维极谐波变换(PHTs)[5]，这种变换成功地应用于图像水印[6]，模式识别[7]，指纹分类等。然而，PHTs的缺陷是在高阶时表现出不稳定性，极谐波复指数变换(PCET)在低阶时就可能表现出不稳定性，极大地限制了PHTs的广泛应用。

目前，学者们针对PHTs的缺点提出了很多改进算法。Singh等[8]提出了基于数值积分的计算框架，同时降低了几何误差和数值积分误差。Yang等[9]提出利用极坐标分区，利用复指数和三角函数的内在递推关系以提高准确度和数值稳定性。Wo等[10]基于PCET，PCT和PST，设计出三种类型的旋转不变性正交矩，这三类矩的特点就是每种矩依赖于一个参数的值，因此只适用于某些特定的场合，在现实中是很难应用。

本文提出一种极谐波正—余弦变换(PCST)，利用正—余弦函数构造新径向内核来实现稳定性，在图像表示方面，该算法较传统方法更适合于高阶矩的情况，同时具有旋转不变性，图像表示性能优越。

1PHTs存在的问题

1.1PHTs定义

2010年，Pew-Thian Yap等[5]提出了一组基于二维变换的极谐波变换(PHTs)，包括极谐波复指数变换(PCET)，极谐波余弦变换(PCT)和极谐波正弦变换(PST)，复指数函数和三角函数具有计算简单的优点，而且具有正交性，因此用来构建矩。

PHTs的内核是基于极坐标空间在单位圆内定义的正交复函数[11]，而图像是在离散域定义，因此，转换到直角坐标系为：

(1)

其中，

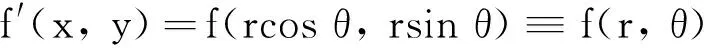
给定一副M*N的图像f(m,n),当m=0,1,2,…,M-1 ，n=0,1,2,…,N-1, 把图像映射到(xm,yn)∈[-1,1]×[-1,1]，

其中

(2)

可推出：

设T是常数， 阶数n和重复度l的限定条件如下:

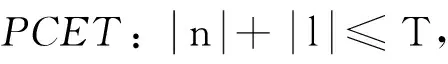
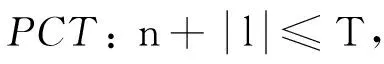
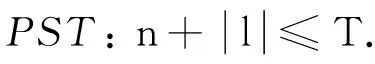
1.2高阶PCET数值不稳定

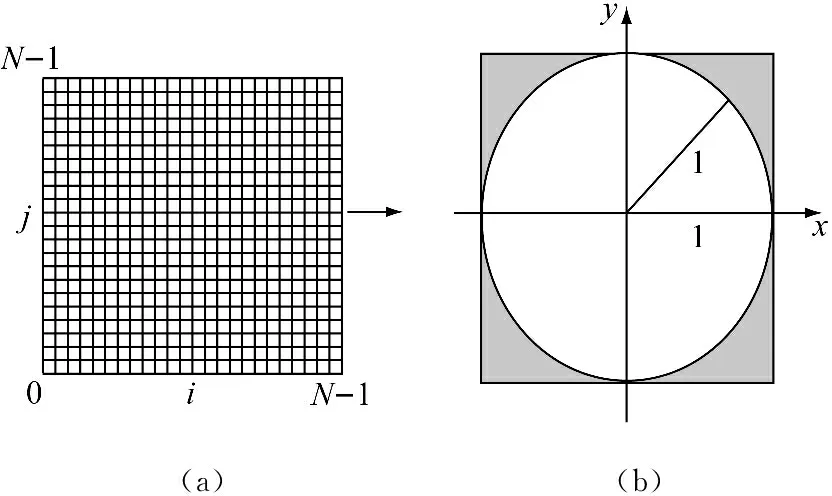
PHTs的内核是一组定义在单位圆内的极坐标空间的正交多项式[12]，如图1所示。

径向内核的数量和径向内核的零分布是评价径向内核的两个重要指标，径向内核Rn(r)为零的数目对应于矩所表示的图像的高频分量，径向内核的零分布关系图像的可压缩程度[12]。

(a)(b)

图1(a)图像平面 (b)图像平面从方形到圆形的映射

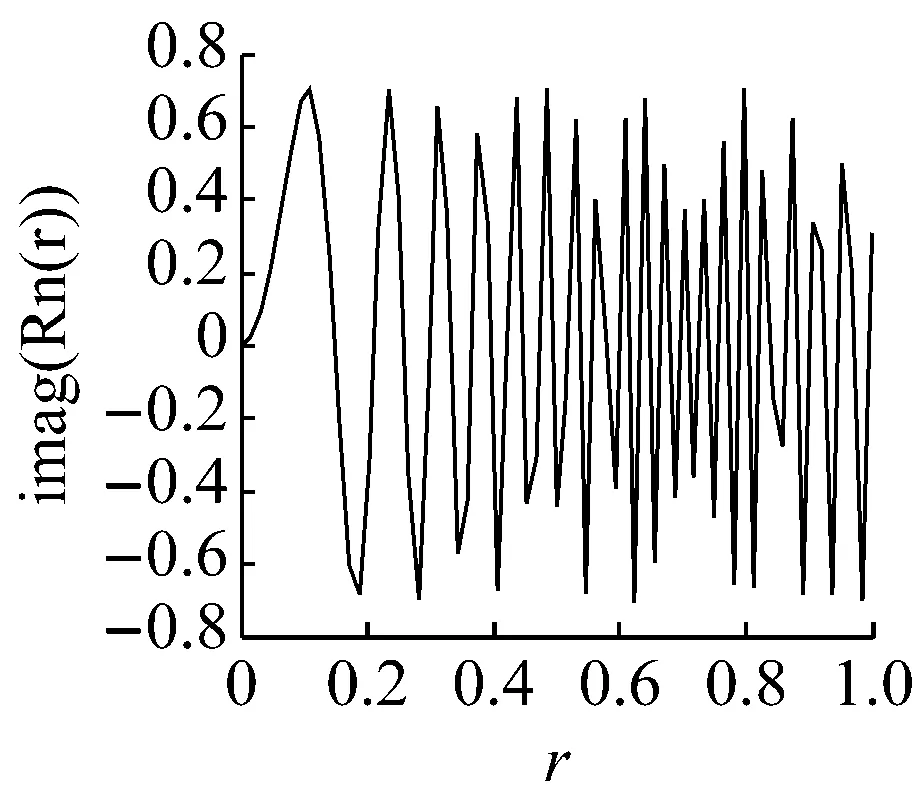
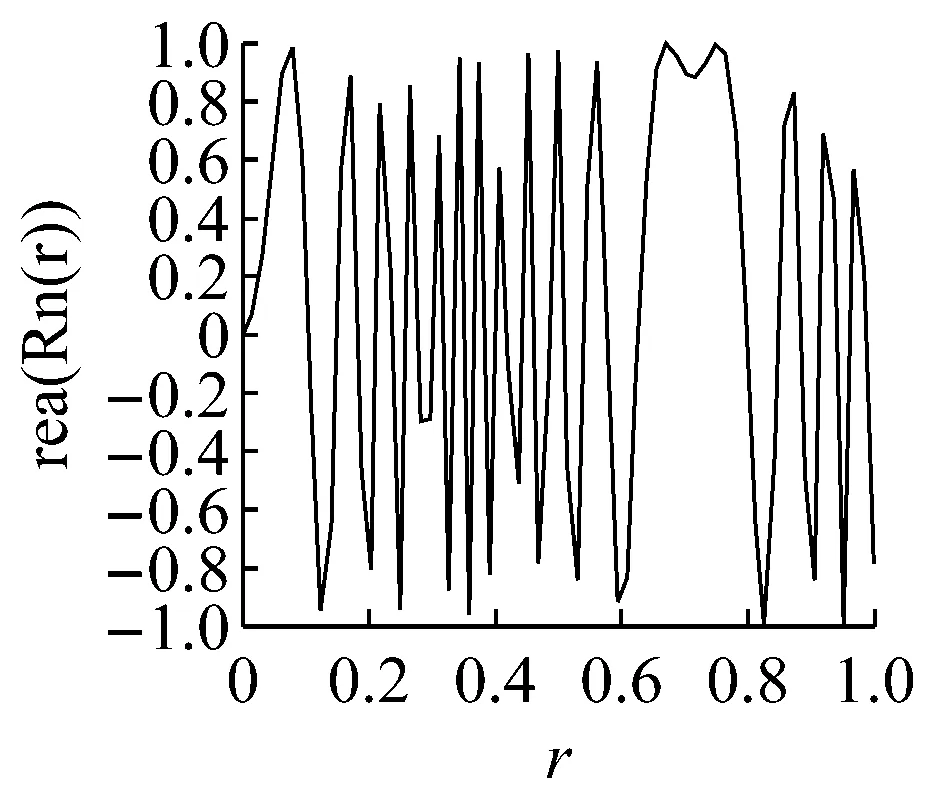
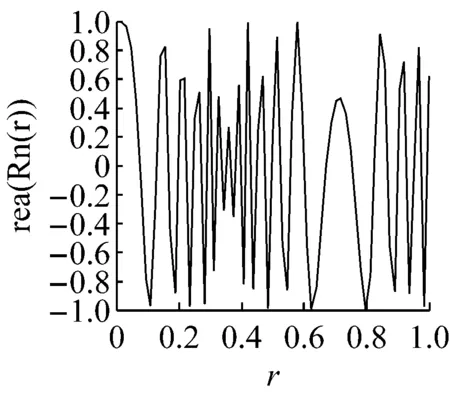
把N×N图像映射到单位圆，半径r为N/2。给定一个128×128图像映射到单位圆，半径分成64份，该128×128图像的PCET的径向内核示于图2。

(a)

(b)

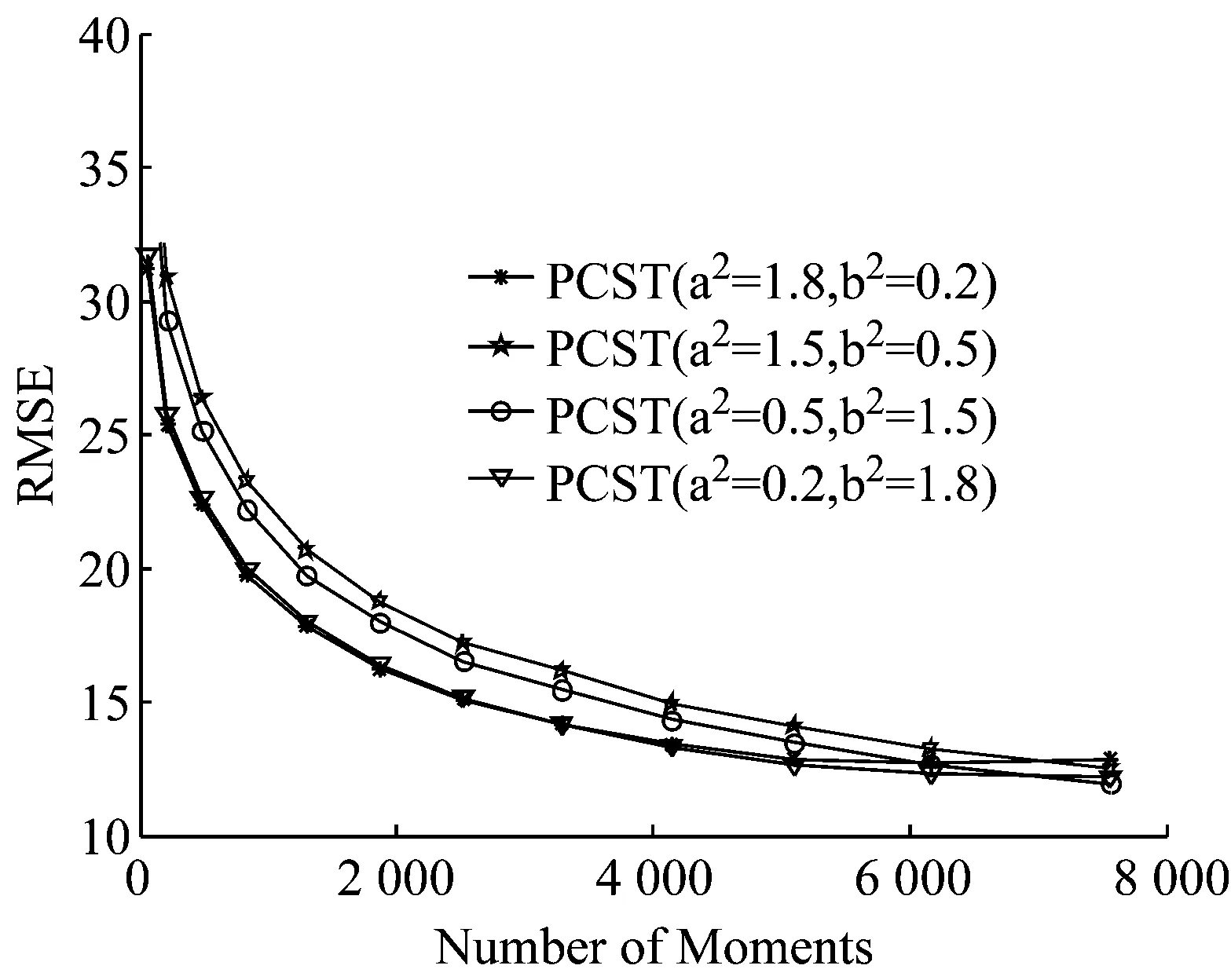
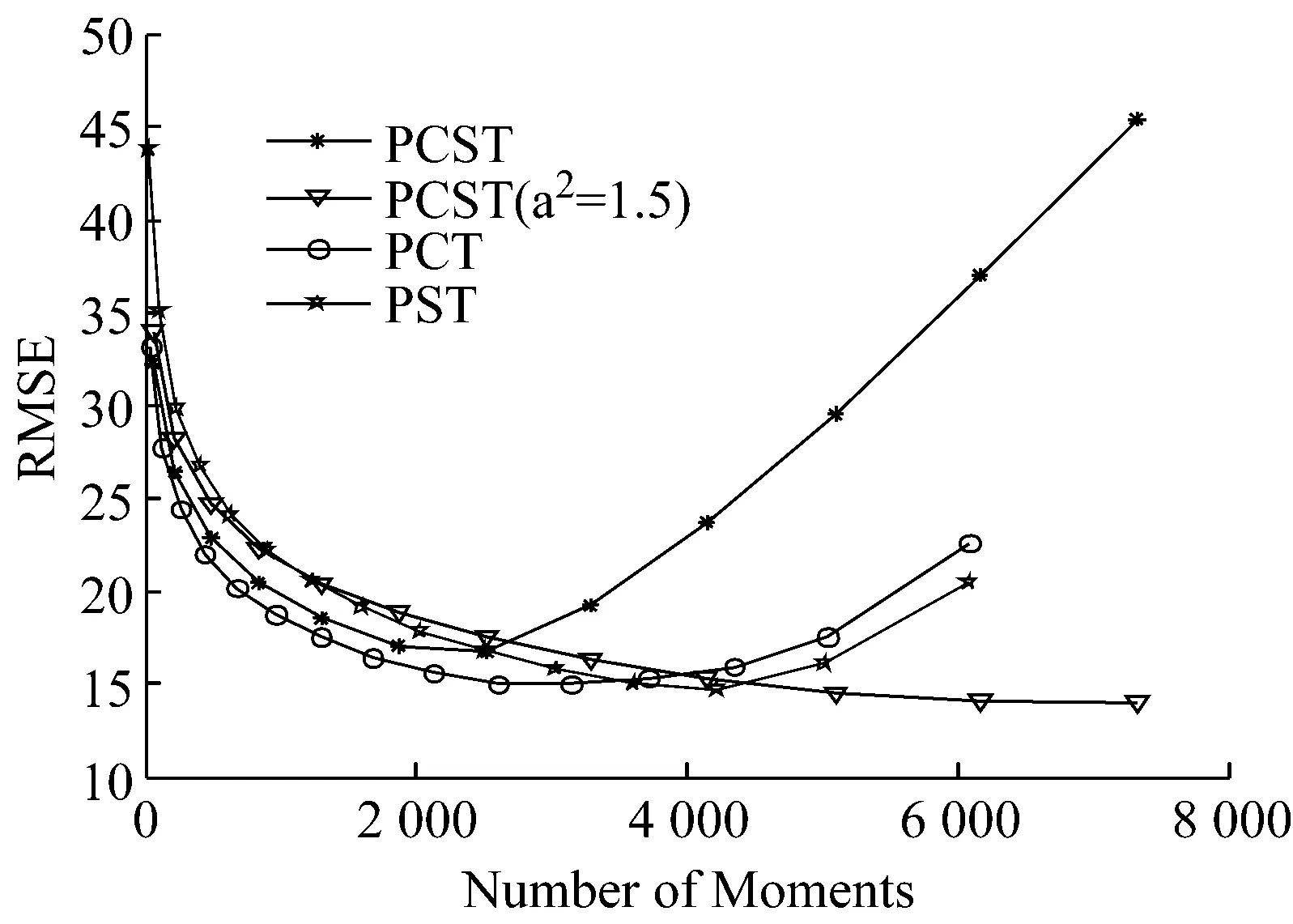
从图2可见，PCET的径向内核没有完全覆盖0.6

2极谐波正—余弦变换

综观现有的文献，几乎没有是通过重构径向核函数来提高稳定性的。本文提出一种使用正—余弦函数作为径向内核的极谐波正—余弦变换(PCST)，所提出的径向内核的零数量和分布都优于传统的PHTs，在用高阶矩表示图像能力方面PCST明显优于PHTs。

2.1PCST的定义

阶数n重复度l的极谐波正—余弦变换定义为:

(3)

内核函数Hnl(r,θ)可以分为径向和环向部分：

(4)

其中包含正—余弦函数的径向部分为：

(5)

满足正交条件:

得：

πδnn′δll′

(6)

因子1/π是规范化因子，对内核函数微调如下:

(7)

得

(8)

图像f(r,θ)用PCST以α角度逆时针旋转的相关系数为fα(r,θ)=f(r,θ-α):

Mnle-ilα

(9)

(10)

其中nmax, nmin, lmax和lmin分别代表PCST的阶数和重复度的最大值和最小值。

2.2分析PCST

(a)

(b)

3实验

3.1实验设置

在本节中，通过一些实验来验证PCST的性能。首先，讨论参数a和b对图像重建的影响。其次，通过实验比较PHTs与PCST在图像表示方面的性能；最后，验证PCST的旋转不变性。为了验证提出的PCST方法能适应不同的场合，设置了不同的阶数n和重复度l。

3.2a和b两个参数对PCST的影响

参考文献在[5]中，原始图像f(r,θ)和重建图像(r,θ)之间的差别使用均方根误差(RMSE)来衡量：

(11)

选3幅大小为128×128的图像用来测试，a和b的平均RMSE值见图3，当参数a，b取不同的值时，即使矩的数目增大到近8 000，PCSTs仍然具有数值稳定性，相比PCET，PCT和 PST效果更优。

参数a和b对PCSTs的RMSE值的影响是很小的，通过实验来验证，选择4组值a2=1.8，b2=0.2， a2=1.5， b2=0.5， a2=0.5， b2=1.5， a2=0.2， b2=1.8，并分别绘出曲线，可得出RMSE随着矩的增加而减小。根据参数a的值的变化，分为两组：第一组是a2∈(0，1)，第二组是a2∈(1，2)，图像的矩的数量限制在7 000以内。从图4的实验结果可以看出，第一组使用矩的数量超过7 000后的效果反而比第二组的效果好，两条曲线在7 000的时候交汇并达到较小的值。事实上，第一组是局部传统的PST，第二组是加强的PCT。因此，参数a和b的值的变化，不会对PCST有较大的影响，这种特性使得PCST对特定的场景具有更好的适应性。

图4　参数a和b的不同值确定的PCST的RMSE曲线

基于图4的结果分析，选择a2=1.5， b2=0.5来进行下面的实验。

3.3图像重建

为了验证所提出的PCST的性能，将提出的PCST与传统的方法进行实验比较。

CSIQ数据库[13]的图像广泛用于图像处理，本实验从CSIQ数据库抽取30副图像用来测试，如图5所示，每副图像大小256×256，它涵盖了不同的主题，如城市风景、动物、风景湖泊、山、植物等，测试之前将30副图像调整成128×128像素。

图5　用于图像重构的30副图像

其中一幅图像的重建实例示于图6，图像b组和c组的矩的数量分别是61，481，2 521，3 121，3 961，6 613，7 321，7 565；图像d组和e组的矩的数量分别是64，484，2 601，3 136，4 096，6 724，7 396，7 569。PCET和PCST使用相同数量的矩；PCT和PST使用相同数量的矩。因无法对四种算法使用相同数目的矩进行测试，但使用矩的数量非常接近，分别为7 565和7 569，数量只差4个，理论上也是可行的，在图像重构过程中，随着矩的数量增加，重建的图像越来越接近于原始图像。从图4可得出，PHTs算法当矩的数量快速增加时，它的数值稳定性突然变差，而本文提出的PCST算法性能较好。

(a)

(b)

(c)

(d)

(e)

(a)原始图像(b)极正弦余弦变换(c)极复指数变换(d)极余弦转换(e)极正弦转换

图7显示了这30副图像的平均RMSE的曲线，从中得出PCST算法比PHTs算法的数值稳定性要好，特别是优于PCET算法，而且当矩的数量超过2 600以后，PCET算法的RMSE值快速增加，PCT和PST这两种算法也有类似的问题，当矩的数量分别达到3 100和4 200时，它们的RMSE值也快速增加，然而，本文提出的PCST算法依然保持下降的趋势。因此，本文的算法用于图像表示时，在高阶矩情况下依然能够保持数值稳定性。

图7　PCSTs和PHTs的平均RMSE值

3.4旋转不变性

为了验证PCST的旋转不变性，将图像大小调整为128×128，并按照8个角度进行旋转，PCST算法中nmin的值设为0，nmax的值设为3。PCST算法的旋转后的结果示于图8，从图8可以看出，无论怎样旋转图像，其矩的模值是保持不变的，PCST具有旋转不变性。

(a)

(b)

图8(a)表示平面图像的原始图(b)从左到右(从上到下)旋转的角度分别为：30°， 60°， 120°， 155°，200°， 255°，300°and 345°

4结论

本文提出了一种极谐波正—余弦变换(PCST)算法，通过实验验证，与PHTs算法相比，它能够在高阶矩时仍能保持数值稳定性，而且具有旋转不变性。因此，PCST算法可广泛地应用于图像检索、人脸识别等领域。

[1]F. Zernike. Beugungstheorie des schneidenver-fahrensund seiner verbesserten form, der phasenkon-trastmethode[J]. Physica, 1934(1): 689-704.

[2]A. B. Bhatia, and E. Wolf. On the circle polynomials of Zernike and related orthogonal sets[J]. Mathematical Proceedings of the Cambridge Philosophical Society, 1954 (50): 40-48.

[3]Y. Sheng, and L. Shen. Orthogonal FourierCMellin moments for invariant pattern recognition[J]. Journal of the Optical Society of America, 1994(11): 1748-1757.

[4]G. Amu, S. Hasi, X. Yang, and Z. Ping. Image analysis by pseudo-Jacobi (p = 4, q = 3)Fourier moments[J]. Applied Optics, 2004(43): 2093-2101.

[5]P. -T. Yap, X. Jiang, and A. C. Kot. Two-dimensional polar harmonic transforms for invariant image representation[J]. IEEE Trans. Pattern Anal. Mach. Intell, 2010(32): 1259-1270.

[6]石红梅. 一种强鲁邦性的图像数字水印算法的设计[J]. 常州信息职业技术学院学报，2011(6)：36-39.

[7]T. V. Hoang, and S. Tabbone. Generic polar harmonic transforms for invariant image description[C]. Proc. of the 18th IEEE International Conference on Image Processing, Brussels, Belgium, 2011: 845-848.

[8]C. Singh, and R. Upneja. Accuracy and numerical stability of high-order polar harmonic transforms[J]. 2012(6): 617-626.

[9]Z. Yang, and S. Kamata. Fast polar harmonic transforms, Proc. of the 11th Int. Conf. on Control,Automation[J]. 2010: 673-677.

[10]Y. Wo, and J. Xu. Accurate and Fast Harmonic Transform of Polar Coordinates[J]. Journal of South China University of Technology (Natural Science Edition), 2012(40): 23-29.

[11]T. V. Hoang, and S. Tabbone. Generic polar harmonic transforms for invariant image representation,Image and Vision Computing[J]. 2014(32): 497-509.

[12]S. Liao, and M. Pawlak. On the Accuracy of Zernike Moments for Image Analysis[J]. 1998(20): 1358-1364.

[13]E. C. Larson and D. M. Chandler. “Categorical image quality (CSIQ)database,” [Online]. Available: http://vision.okstate.edu/csiq.

收稿日期：2016-03-14

基金项目：南通市科技计划项目(BK2014022)

作者简介：孙克争(1983-)，男，讲师，主要研究方向：软件设计、图像处理和信息安全

中图分类号：TP 391

文献标志码：A

文章编号：1672-2434(2016)03-0018-05

An Improved Image Representation Algorithm

SUN Kezheng1TANG Lijuan1,2

(1. Jiangsu Vocational College of Business, Nantong 226011, China；2. School of Information and Electrical Engineering, China University of Mining and Technology, Xuzhou 221116, China)

Abstract：Since the introduction of polar harmonic transforms, it has been widely used in image analysis and pattern recognition because it is simple in calculation. However, PHTs shows instability in higher-order transformation and harmonic complex exponential transform (PCET) may exhibit instability in the low order transformation. In order to design the moment which can be widely used in image representation, a new Cosine-Sine Transform Polar (PCST) is proposed, which uses a new radial kernel function to achieve reliable stability. The experimental results show that the stability of image representation is better than that of PHTs, especially in the higher order moment. And it has the rotation invariance, and keeps the stability of the image.

Key words：PHTs; rotation invariants; PCST