矩阵的初等变换在几何学上的应用

孙 卫 卫

(青岛理工大学 琴岛学院，山东 青岛 266106)



矩阵的初等变换在几何学上的应用

孙 卫 卫

(青岛理工大学 琴岛学院，山东 青岛 266106)

摘要：基于矩阵的初等变换法化简二次型为标准形思想，给出了求与实对称矩阵合同的对角矩阵的定理，并应用到几何学上，即运用矩阵的初等变换来推断一类二次曲线和一类二次曲面的大体形状，并给出了相应的定理性结论。

关键词：初等变换；二次曲线；二次曲面；实对称矩阵；二次型

DOI：10.13757/j.cnki.cn34-1150/n.2016.02.029

对于一般的二次曲线与二次曲面的形状的推断是困难的，用矩阵的初等变换法可以解决这一问题。

1求与实对称矩阵合同的对角矩阵的初等变换法

引入实对称矩阵A与向量x、y：

A所对应的二次型为

f(x1,x2,…,xn)=xTAx

(1)

对于二次型(1)总存在可逆的线性变换[1-2]x=Cy，将其代入(1)式得到此二次型的标准形：

f(x1,x2,…,xn)=yTAy

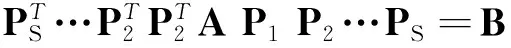
定理1对实对称矩阵A施行一次初等列变换，再施以相同的初等行变换，这样进行若干次就可把A化简成对角矩阵B，并且有A与B合同。

例1求与下列矩阵合同的对角矩阵：

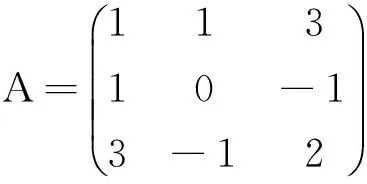
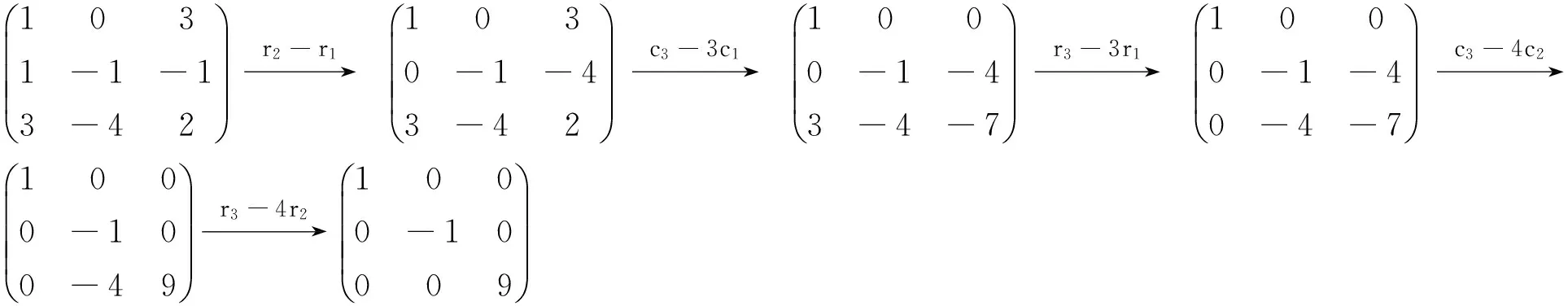
2运用初等变换法推断一类二次曲线的形状

给定二次曲线方程

a11x2+a22y2+2a12xy+c1=0

(2)

引入实对称矩阵与3个向量

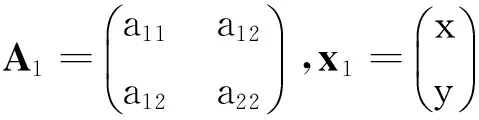
由定理1知，可通过初等变换法求出与A1合同的对角矩阵B1，这里设B1=diag(d1,d2)，则有如下定理：

定理2形如(2)式的二次曲线的大体形状，由d1、d2及c1的正负确定。

(3)

(4)

由于正交变换保持向量的内积和长度不变[3]，因此(2)式与(4)式所表示的曲线形状相同。 因为A1与B1合同且A1与diag(λ1,λ2)合同，可知B1与diag(λ1,λ2)合同，故B1=diag(d1,d2)与diag(λ1,λ2)具有相同的秩与正惯性指数，所以(3)式与(4)式表示同一种类型的二次曲线，故(2)式与(3)式所表示的曲线形状大致相同，即可得形如(2)的二次曲线的大体形状，由d1、d2及c1的正负确定。

例2判定下列二次曲线为何种二次曲线

(1)x2+3y2-2xy-1=0；

(2)x2-y2-2xy+1=0。

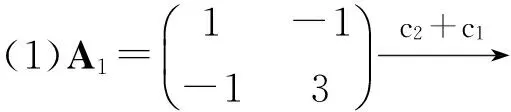
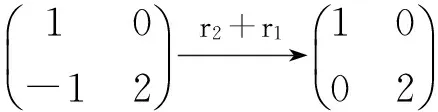
由定理2，x2+3y2-2xy-1=0与x2+2y2-1=0的形状大致相同，因此x2+3y2-2xy-1=0，为椭圆。

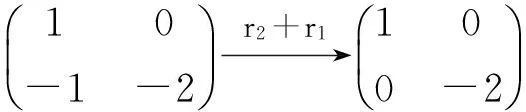
由定理2知x2-y2-2xy+1=0与x2-2y2+1=0的形状大致相同，因此x2-y2-2xy+1=0，为双曲线。

3运用初等变换法推断一类二次曲面的形状

给定二次曲面方程

b11x2+b22y2+b33z2+2b12xy+

2b13xz+2b23yz+c2=0

(5)

并引入实对称矩阵

(6)

(7)

例3判定下列二次曲面为何种二次曲面。

(1)x2+z2-2xy+1=0；

(2)x2+2y2+6z2-4xz-4yz-2=0。

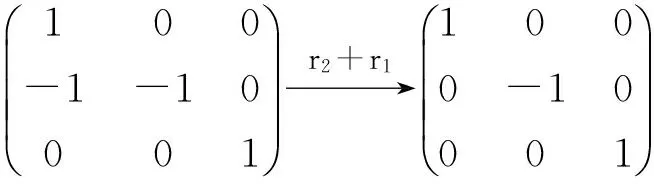
由定理3知x2+z2-2xy+1=0与x2-y2+z2+1=0的形状大致相同，因此x2+z2-2xy+1=0表示椭圆锥面。

由定理3知x2+2y2+6z2-4xz-4yz-2=0与x2+2y2-2=0的形状大致相同，因此x2+2y2+6z2-4xz-4yz-2=0表示椭圆柱面。

参考文献:

[1] 吴赣昌. 线性代数(理工类)[M]. 4版. 北京: 中国人民大学出版社, 2011: 78-83.

[2] 黄益生. 高等代数 [M]. 2版. 北京: 清华大学出版社, 2014: 153-160.

[3] 杨文茂. 空间解析几何 [M]. 2版. 武汉: 武汉大学出版社, 2004: 201-207.

[4] 同济大学数学系. 高等数学(下册)[M]. 6版. 北京：高等教育出版社, 2007: 20-22.

[5] 华东师范大学数学系. 数学分析(下册)[M]. 4版. 北京: 高等教育出版社, 2010: 52-55.

[6] 徐森林. 数学分析(第三册)[M]. 2版. 北京: 清华大学出版社, 2007: 43-45.

ApplicationofElementaryTransformationofMatrixinGeometry

SUNWei-wei

(QingdaoCollege,QingdaoTechnologicalUniversityQingdao,Qingdao,Shandong266106,China)

Abstract:Quadraticformcanbesimpliedtostandardformbyusingelementarytransformationmethod.Inspiredbythis,inthispaper,theelementarytransformationmethodisgiven.Thismethodisemployedtofindthediagonalmatrixthatiscongruentwiththerealsymmetricmatrix.Thenthecorrespondingtheoremisgiven.Fromthispointofview,theelementarytransformationofthematrixisappliedingeometry.Theseshapesofakindofquadraticcurvesandakindofquadraticsurfacesarededucedusingelementarytransformationmethod.Furthermorethecorrespondingrationalconclusionisgiven.

Keywords:elementarytransformation;quadraticcurve;quadraticsurface;realsymmetricmatrix;quadraticform

* 收稿日期：2015-09-22

作者简介：孙卫卫，女，山东烟台人，硕士，青岛理工大学琴岛学院讲师，研究方向为应用数学。E-mail: xiesunweiwei@126.com

中图分类号：O13

文献标识码：A

文章编号：1007-4260(2016)02-0121-03

网络出版时间：2016-06-08 12:57网络出版地址：http://www.cnki.net/kcms/detail/34.1150.N.20160608.1257.029.html