基于PCA-BP神经网络的岩石爆破平均粒径预测*

史秀志,郭　霆,尚雪义,姬露露

(中南大学 资源与安全工程学院，长沙 410083)



基于PCA-BP神经网络的岩石爆破平均粒径预测*

史秀志,郭霆,尚雪义,姬露露

(中南大学 资源与安全工程学院，长沙 410083)

摘要:岩石爆破平均粒径的预测对岩石采装及二次破碎具有重要意义，然而常规的神经网络预测岩石爆破平均粒径存在较大的误差。为更加合理准确预测岩石爆破粒径分布，选取台阶高度与钻孔荷载比(H/B)，间距与荷载比(S/B)，荷载与孔径比(B/D)，炮泥与荷载比(T/B)，粉因数(Pf)，弹性模量(E)和现场块度大小(XB)7个主要影响岩石爆破粒径的因素，并结合BP神经网络较好的预测性，以及主成分分析(PCA)能消除自变量间的相关性和减少BP神经网络输入数据的特点，建立了基于PCA-BP神经网络的岩石爆破粒径预测模型。以48组实测数据为例，对7个影响因素进行主成分分析，最终降为4个主成分，进而将其作为BP神经网络的输入因子，对岩石爆破粒径进行了预测。结果表明：BP神经网络与最小二乘法预测的平均误差分别为15.71%、27.32%，而PCA-BP神经网络预测平均误差仅为9.21%，实现了对岩石爆破粒径的较准确预测。综上所知，PCA-BP神经网络模型为岩石爆破平均粒径预测提供了一种科学、可靠的方法。

关键词:岩石爆破粒径；主成分分析法；BP神经网络；预测模型；最小二乘法

在露天矿爆破作业中，合适的爆破粒径分布不仅有利于矿石的装载和运输，提高采装效率，而且可降低二次破碎带来的风险[1]。因而实现最佳的破岩粒度分布无疑成为了岩石爆破的重点。然而岩石的爆破粒径受爆破设计参数、炸药参数以及岩体性质等因素的影响[2]，且各因素之间又存在极其复杂的非线性关系。传统的爆破粒径预测模型大多为经验或理论模型，其适用范围相对较窄。以人工智能理论为基础对岩石爆破粒径预测的方法主要有：灰色关联理论[3]、模糊逻辑[4]、人工神经网络[5]、支持向量机等[6]。这些方法虽然能够预测岩石爆破粒径，但由于其采用了较多相互关联的指标，使得预测的效率降低。通过主成分分析法对样本数据进行分析，保留主要的影响因子，提高运算效率[7]。此外，BP神经网络具有较强的自学习、自适应能力和非线性映射能力，具有较好的预测功能[8-9]。为此，建立PCA-BP岩石爆破粒径的预测模型，主要考虑了影响岩石爆破粒径的7个主要因素，利用主成分分析法提取出4个主成分作为BP网络的输入因子，以期提高BP神经网络对岩石爆破粒径预测的精度。

1主成分分析基本原理

主成分分析法是在保存原有主要信息的前提下，对多个影响因子进行降维处理得到相互之间没有关联的综合指标[10]。这种方法能够将原本复杂的多指标问题简易化，数量相对较少的综合指标在计算中极大的提高了运算效率，使原本冗余的计算过程得到简化，同时保证了计算的精确性，最终得到可靠的计算结果。

关于n个样品p个变量x1、x2…xp的问题(n>p)，对其原数据进行整理，得到原始数据矩阵为

(1)

为消除不同指标的量纲不同会造成指标的不可公度性，在运用主成分分析法处理之前需通过式(2)对各指标数据进行无量纲化处理。

(2)

数据无量纲化后的矩阵用x表示，即将x=(x1,x2,…,xp)′的p个变量综合成p个新变量，新的综合变量可由原来的变量p线性表示，即

(3)

并满足

(4)

式中，k=1,2,…,p。系数uij满足以下原则：

(1)yj与yij( i≠j,i, j=1,2,…,p)无关联性。

(2)yp为 y1,y2,…,yp-1都不相关的x1,x2,…,xp所有线性组合中方差最大者。

利用上述方法可计算出原变量第1，第2，…，第p个主成分所对应的综合变量 y1,y2,…,yp。且所得综合变量的方差占总方差的比重逐步降低。主成分的选取个数通过累积方差贡献率的计算来确定，方差贡献率过大则保留的数据信息更多，但计算量也会随之增大；方差贡献率过小虽然提高了运算效率，但会造成信息的大量丢失，影响最终计算结果的准确性。通常情况下以累积方差贡献率大于80%为标准来确定所要选取的主成分[11]。

2岩石爆破粒径预测的神经网络模型

2.1基本原理

BP神经网络具有很强的多层次、非线性映射能力，能较好地解决少数据、贫信息、不确定性问题，且不受非线性模型的限制[12]。最优的输入、输出因子以及学习、训练样本是建立合理、高效的BP神经网络预测模型的关键。一般情况下选取由输入层、隐含层和输出层组成的3层BP神经网络计算模型[13-15]。网络原理如图1所示。

2.2算法简介

在样本数据输入神经网络之前需对样本进行归一预处理，以此来确保神经网络的收敛性和高效性。对于给定训练样本的输入，在网络输出能准确逼近给定训练样本输出时，该网络完成了训练过程[16]。BP神经网络预测模型算法流程如图2。

转换函数f为Sigmoid函数

(5)

误差函数为

(6)

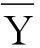
(7)

任意选取权系数初值，隐层与输入层的权值调整量为

(8)

(9)

3PCA-BP神经网络预测岩石爆破粒径模型的建立与应用

3.1PCA-BP网络预测岩石爆破粒径模型的建立

影响岩石爆破粒径的主要因素有爆破设计参数、炸药参数和岩石性质等。爆破设计参数主要包括台阶高度(H)、钻孔荷载(B)、炮泥(T)、间距(S)和孔径(D)五个因素。一些爆破研究人员认为爆破设计参数应为比率[2]，以台阶高度与钻孔荷载比(H/B)，间距与荷载比(S/B)，荷载与孔径比(B/D)，炮泥与荷载比(T/B)作为爆破设计参数。粉因数(Pf)为反映炸药性质的参数。基于爆破设计参数、弹性模量和现场块度大小等7个参数建立PCA-BP网络岩石爆破粒径预测模型。

首先使用主成分分析法对样本影响因子进行降维处理，将得到的综合变量作为BP神经网络的输入样本，通过迭代计算后输出结果，最终建立了基于PCA-BP网络的岩石爆破粒径预测模型，见图3。

3.2相关性分析

借助SPSS计算原始变量间的相关系数，且选取输入因素为[2]：台阶高度与钻孔荷载比(H/B)，间距与荷载比(S/B)，荷载与孔径比(B/D)，炮泥与荷载比(T/B)，粉因数(Pf)，弹性模量(E)和现场块度大小(XB)。输出因素为爆破岩石的粒径(X50)，各参数具体数值见表1。选用Pearson检验计算相关系数，并得到相关系数矩阵如表2所示。

由表2可知:输入的样本数据中部分指标间存在多重相关性，为提高计算精度，需对其利用主成分分析法进行降维处理。

3.3主成分分析

为消除影响因子之间由于单位或者数量级不同造成的误差，利用式(2)对数据进行无量纲化处理。

借助SPSS得到相关系数矩阵特征值，进而得到各成分的贡献率(见表3)。由3表可知：前四个成分累计贡献率已大于80%，及其已达到了主成分方差占总方差80%以上的要求。因此通过主成分分析，7个主成分可以降为4个，故只需求出第1、第2、第3和第4主成分y1、y2、y3、y4即可。表4为主成分因子荷载矩阵，由此得到各因子表达式

y1=-0.0589x1-0.7340x2+1.0823x3+0.2450x4+

0.5298x5-0.2687x6-0.5808x7

(10)

y2=0.4627x1-0.6691x2-0.3943x3-0.4055x4+

0.4490x5-0.5885x6+0.5750x7

(11)

y3=0.4599x1+0.3470x2-0.0399x3-0.5503x4+

0.1376x5-0.1195x6-0.6111x7

(12)

y4=0.3876x1-0.3136x2-0.0314x3+0.1932x4-

7027x5-0.1666x6-0.1838x7

(13)

根据上述表达式对无量纲化后的数据进行主成分分析计算，部分计算数据见表5。

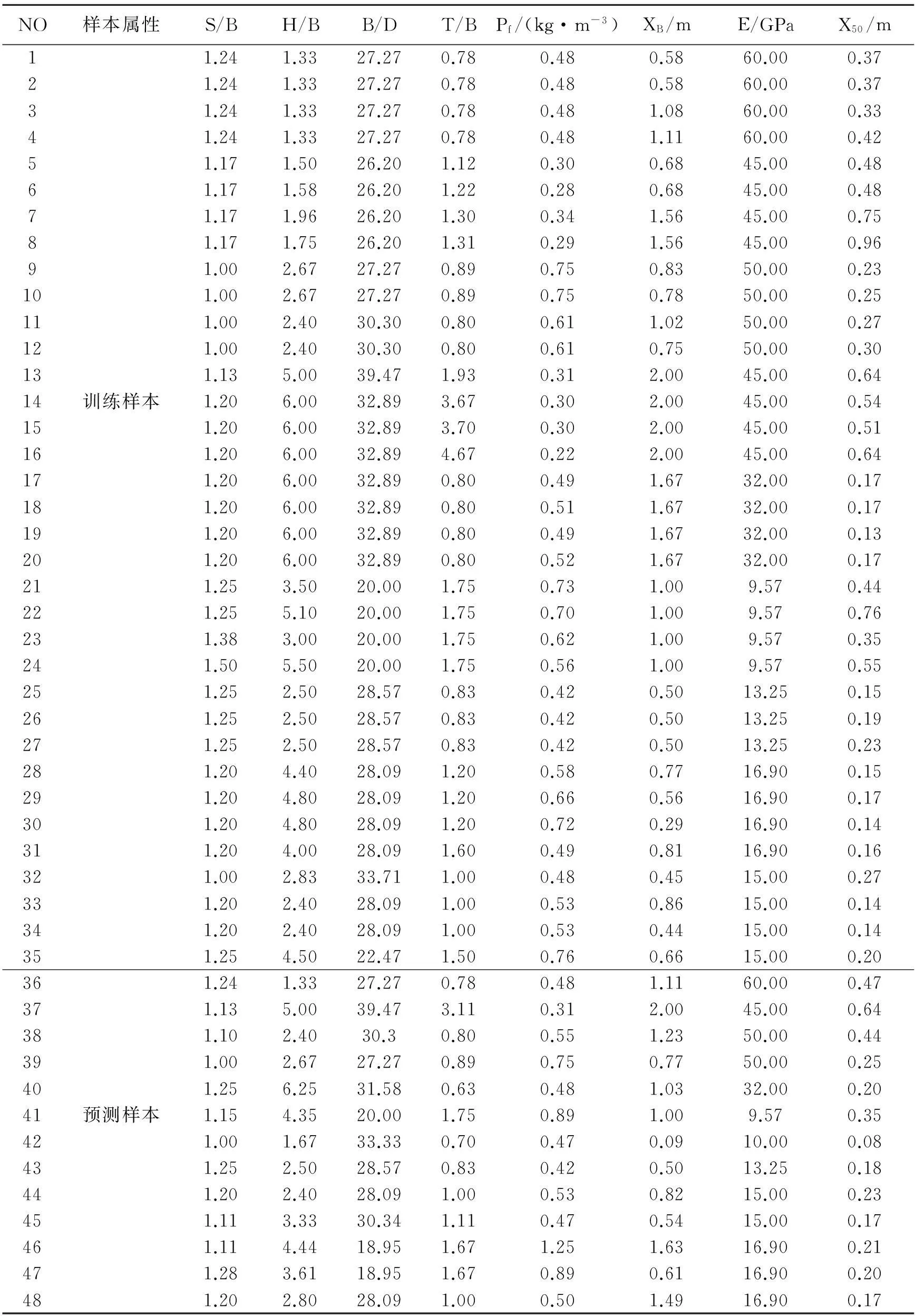
表1　影响岩石爆破粒径因素及其样本统计

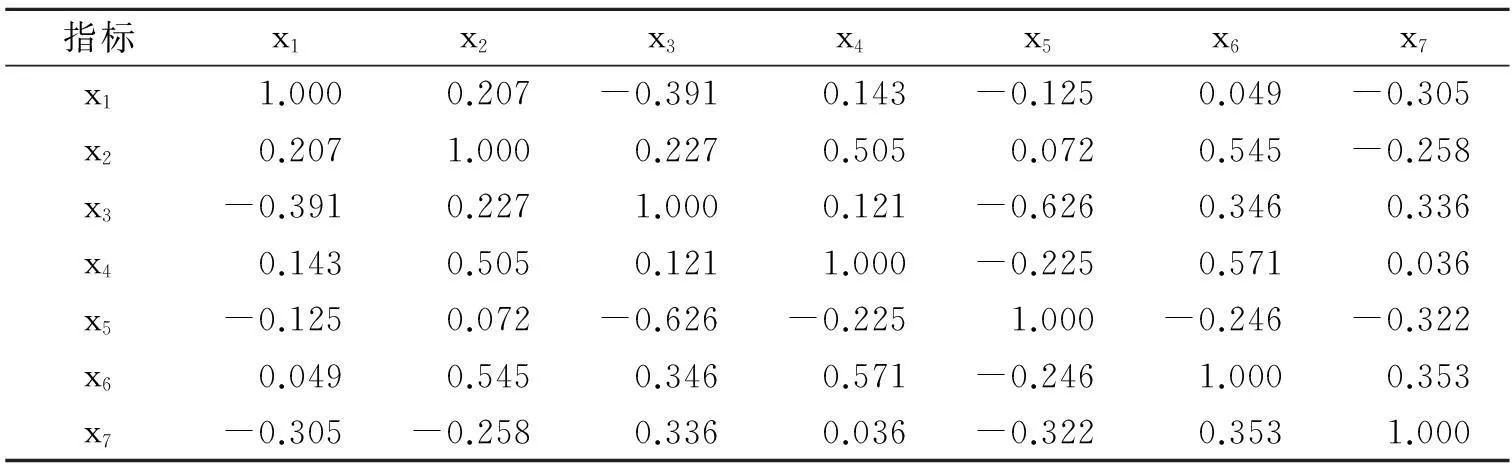
表2　各因素间的Pearson相关系数矩阵

表3　主成分贡献率

表4　主成分因子荷载矩阵

3.4BP网络模型的设计、训练与预测

以上文y1、y2、y3、y4作为输入因素，岩石爆破粒径(X50)为输出因素，学习率0.9，冲量系数0.7。通过计算得隐含层个数为7，最终确定4∶7∶1的3层BP神经网络模型。将主成分分析计算后的数据作为训练与预测样本，其中前35组为训练样本，后13组为预测样本。预测样本的预测结果见表5。

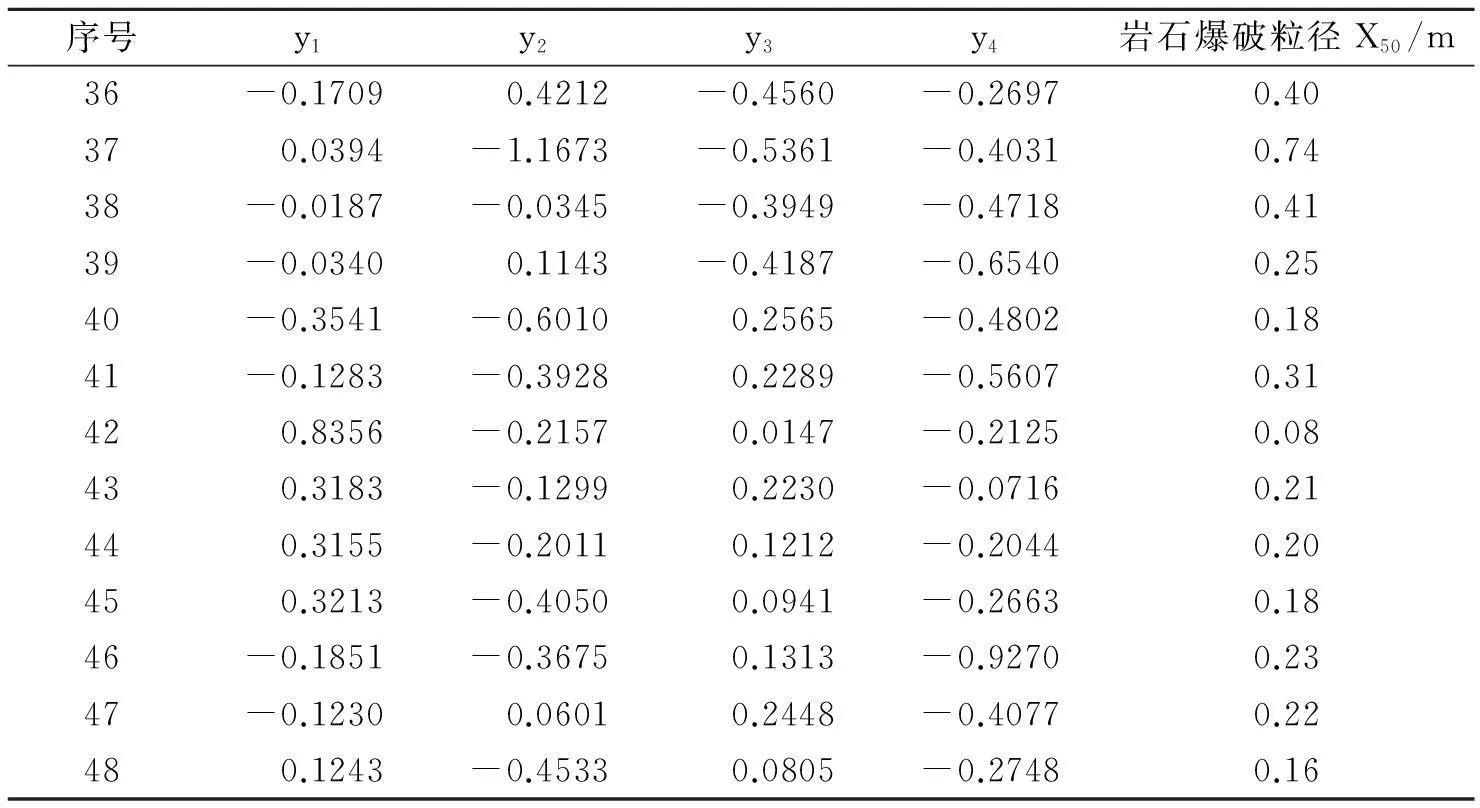
表5　主成分分析后的部分数据

将PCA-BP神经网络与BP神经网络、最小二乘法的预测结果进行对比可得表6，由表6可知：BP神经网络、最小二乘法预测的平均相对误差分别为15.71%、27.32%，而PCA-BP神经网络模型预测的平均相对误差仅为9.21%。PCA-BP网络的预测结果达到较理想的水平。

图4为最小二乘法预测值、BP神经网络预测值、PCA-BP神经网络预测值和实测值曲线，由图4可知，最小二乘法的预测值曲线与实测值曲线普遍偏移较大，BP神经网络、PCA-BP神经网络的预测值曲线与实测值曲线的趋势一致。究其原因是最小二乘法对影响因素与爆破粒径进行线性拟合，而爆破影响因素与粒径间的关系可能为非线性，故而最小二乘法拟合误差较大。BP神经网络拥有较好的学习和映射能力，同时其又具有自学习功能可以不断用新数据训练网络，修正预测模型。因而BP神经网络较最小二乘法预测结果准确。而PCA-BP神经网络利用主成分分析法去除参数间的相关性，提高了模型的预测精度，使得PCA-BP神经网络较BP神经网络预测结果更准确。由此可知PCA-BP神经网络模型的预测结果较最小二乘法和BP神经网络准确，与实测值的拟合度更好。

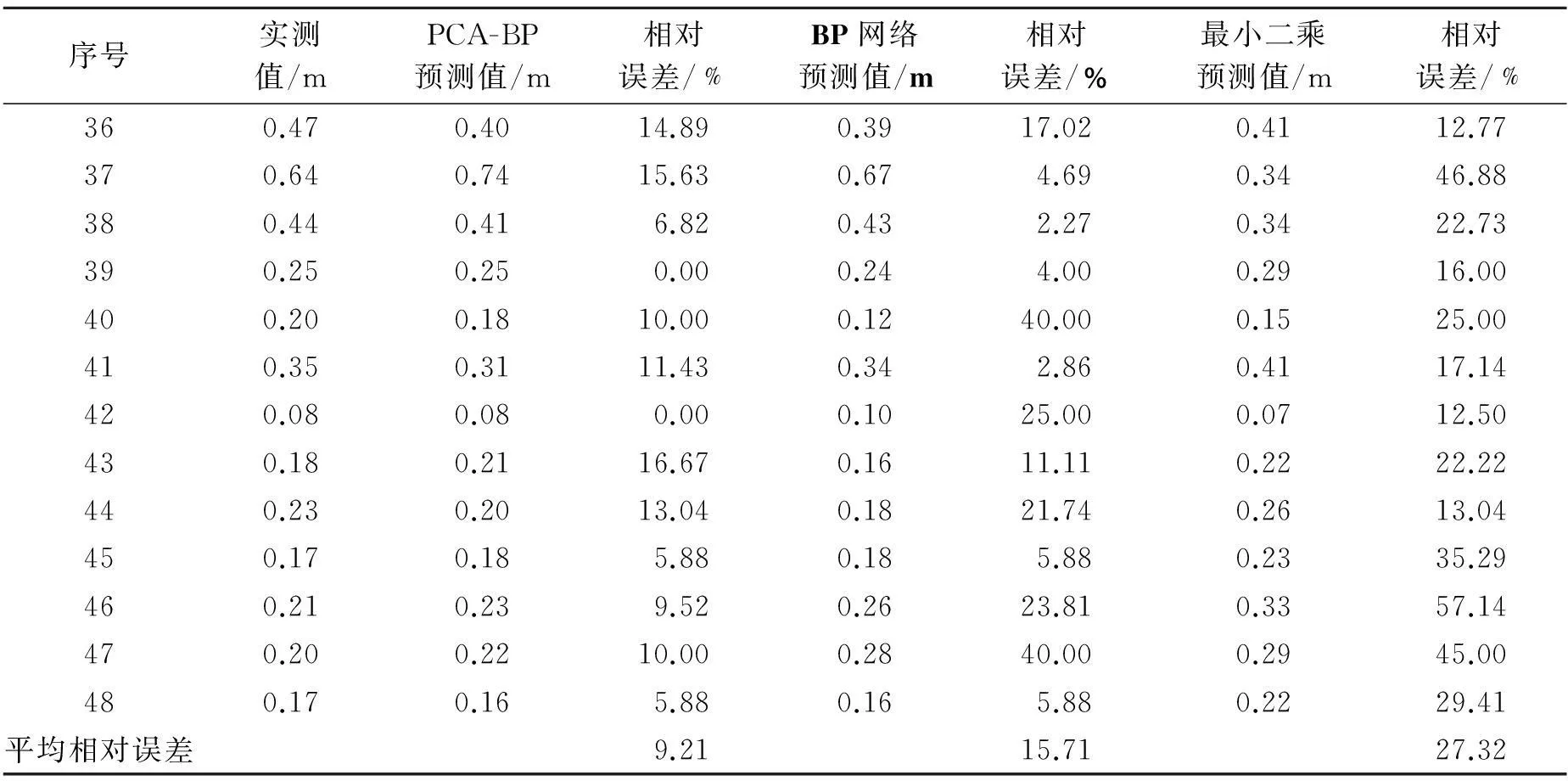
表6　最小二乘法、BP神经网络与PCA-BP神经网络预测结果对比

4结论

针对神经网络和最小二乘法预测岩石爆破粒径存在误差较大的问题，将主成分分析法与BP神经网络结合，建立了PCA-BP神经网络预测模型，分析了PCA-BP神经网络预测岩石爆破平均粒径的效果，最终得到以下三方面的结论，具体论述如下：

(1)PCA-BP神经网络模型预测的平均相对误差控制在10%以内，预测精度较最小二乘法和未经主成分分析法处理的神经网络有着显著的提高。

(2)主成分分析法有效解决了自变量间的多重相关性，同时减少了BP神经网络的输入神经元个数，在保证计算精度的同时有效的降低了运算量，表明PCA-BP网络模型对岩石爆破粒径预测具有较好的改进意义。

(3)基于PCA-BP神经网络建立的岩石爆破粒径预测模型，其预测结果良好。表明PCA-BP神经网络预测模型能够对岩石爆破提供可靠、科学的指导。

参考文献(References)

[1]SHI Xiu-zhi,ZHOU Jian,WU Bang-biao,et al.Support vector machines approach to mean particle size of rock fragmentation due to bench blasting prediction[J].Transactions of Nonferrous Metals society of China,2012,22(2):432-441.

[2]P H S W-Kulatilake,WU Qiong,HUDAVERDI T,et al.Mean particle size prediction in rock blast fragmentation using neural networks[J].Engineering Geology,2010,114(3/4):298-311.

[3]李斌，许梦国，王平，等.基于灰关联得井下采矿爆破块度分析[J].有色金属(矿山部分),2012,64(6):55-58.

[3]LI Bin,XU Meng-guo,WANG Ping,et al.Blasting fragmentation in underground mine based on Grey Correlation Analysis[J].Nonferrous Metal(Mining Section),2012,64(6):55-58.(in Chinese)

[4]MONJEZI M,REZAEI M,VARJANI A Y.Prediction of rock fragmentation due to blasting in GoI-E-Gohar iron mine using fuzzy logic[J].International Journal of Rock Mechanics and Mining Sciences,2009,46:1273-1280.

[5]MONJEZI M,AMIRI H,FARROKHI A,et al.Prediction of rock fragmentation due to blasting in Sarcheshmeh copper mine using artificial neural networks[J].Geotechnical and Geological Engineering,2010,28:423-430.

[6]潘玉忠，张义平，王强，等.台阶爆破块度的SVM预测模型研究[J].矿业研究与开发,2010,30(5):97-99.

[6]PAN Yu-zhong,ZHANG Yi-ping,WANG Qiang,et al.Study on support vector machines model for prediction of rock fragment size of bench blasting.[J].Mining R & D,2010,30(5):97-99.(in Chinese)

[7]陈建宏，刘浪，周智勇，等.基于主成分分析与神经网络的采矿方法优选[J].中南大学学报:自然科学版,2010,4l(5):1967-1972.

[7]CHEN Jian-hong,LIU Lang,ZHOU Zhi-yong,et al.Optimization of mining methods based on combination of principal component analysis and neural networks[J].Journal of Central South University:Science and Technology,2010,41(5):1967-1972.(in Chinese)

[8]杨凯，陈建宏.基于主成分分析与BP神经网络的冲击地压预测[J].广西大学学报:自然科学版,2012,37(5):997-1003.

[8]YANG Kai,CHEN Jian-hong.Research of rock burst prediction based on combination of principal component analysis and neural network[J].Journal of Guangxi University:Natural Science Edition,2010,37(5):997-1003.(in Chinese)

[9]邬书良，陈建宏，杨姗.基于主成分分析与BP网络的锚杆支护方案优选[J].工程设计学报,2012,19(2):150-155.

[9]WU Shu-liang,CHEN Jian-hong,YANG Shan.Optimization of bolting scheme based on combination of principal component analysis and BP neural network[J].Chinese Journal of Engineering Design,2012,19(2):150-155.(in Chinese)

[10]林杰斌，刘明德.SPSS 10.0与统计模式建构[M].北京:人民统计出版社，2001:185-190.

[11]叶双峰.关于主成分分析做综合评价的改进[J].数理统计与管理，2001,20(2):52-55,61.

[11]YE Shuang-feng.Application and consideration about principal component analysis[J].Application of Statistics and Management,2001,20(2):52-55,61.(in Chinese)

[12]李晓峰，徐玖平，王荫清，等.BP人工神经网络自适应学习算法的建立及其应用[J].系统工程理论与实践，2004(5):1-8.

[12]LI Xiao-feng,XU Jiu-ping,WANG Yin-qing,et al.The establishment of self-adapting algorithm of BP neural network and its application[J].Systems Engineering—Theory & practice,2004(5):1-8.(in Chinese)

[13]李松，刘力军，翟曼.改进粒子群优化BP神经网络的短时交通流预测[J].系统理论与实践,2012,32(9):2045-2049.

[13]LI Song,LIU Li-jun,ZHAI Man.Prediction for Short-term traffic flow based on modified PSO optimized BP neural network[J].Systems Engineering—Theory & Practice,2012,32(1):2045-2049.(in Chinese)

[14]何长虹，黄全义，申世飞，等.基于BP神经网络的森林可燃物负荷量估测[[J].清华大学学报:自然科学版，2011,51(2):230-233.

[14]HE Chang-hong,HUANG Quan-yi，SHEN Shi-fei,et al.Forest fuel loading estimates based on a back propagation neutral network[J].Journal of Tsinghua University:Science and Technology,2011,51(2):230-233.(in Chinese)

[15]李云，刘霁.神经网络与主元分析在采矿工程中的应用[J].中南林业科技大学学报，2010，30(6)：140-146.

[15]LI Yun,LIU Ji.Application of combination of neural networks and principal component analysis in mining engineering[J].Journal of Central South University of Forestry & Technology,2010,30(6):140-146.(in Chinese)

[16]冯岩，王新民，程爱宝，等.采空区危险性评价方法优化[J].中南大学学报:自然科学版,2013,44(7):2881-2888.

[16]FENG Yan,WANG Xin-min,CHENG Ai-bao,et al.Method optimization of underground goaf risk evaluation[J].Journal of Central South University:Science and Technology,2013,44(7):2881-2888.(in Chinese)

Prediction of Mean Particle Size of Rock Blast based on Combination of PCA and BP Neural Networks

SHIXiu-zhi,GUOTing,SHANGXue-yi,JILu-lu

(School of Resources and Safety Engineering,Central South University,Changsha 410083,China)

Abstract:The prediction of mean particle size of rock blast is of great importance in rock transportation and secondary rock breaking.However,the conventional neural networks have relatively large errors in mean particle size prediction.To predict the particle size distribution of rock blast fragment more precisely and accurately,seven main factors influencing the particle size of rock blast fragment were chosen,including the ratio of bench height to drilled burden(H/B),ratio of spacing to burden(S/B),ratio of burden to hole diameter(B/D),ratio of stemming to burden(T/B),powder factor(Pf),modulus of elasticity(E) and in-situ block size(XB).In addition,the BP neural networks has a good predictability and the principal component analysis(PCA) can eliminate the correlation between independent variables and reduce the BP neural network input data.Then the particle size of rock blast fragment predict model was built,combines with the PCA and BP neural networks.Furthermore,the PCA-BP method was tested on 48 group data,and a principal component analysis was performed on the seven factors which were eventually reduced into four main factors.Then the four factors were used as BP neural networks input to predict particle size of rock blast fragment.Results show that,the average errors of BP neural networks and the least square method are 15.71% and 27.32%,while the same reference value of PCA-BP neural networks prediction is only 9.21%.In conclusion,the PCA and BP neural networks model provides a scientific and reliable method for the prediction of mean particle size of rock blast fragment.

Key words:particle size of rock blast fragmentation; principal component analysis; BP neural networks; prediction model; least squares method

doi:10.3963/j.issn.1001-487X.2016.02.011

收稿日期:2016-01-29

作者简介:史秀志(1966-)，男，博士、教授、博士生导师，从事爆破工程与安全科学技术研究，(E-mail)csublasting@163.com。 通讯作者:郭霆(1989-)，男，硕士研究生，从事采矿工艺与爆破方面的研究工作，(E-mail)csubaopo@163.com。

基金项目:国家科技支撑计划项目(2013BAB02B05)

中图分类号:TD235.1

文献标识码:A

文章编号:1001-487X(2016)02-0055-07