考虑脑力负荷的自治装配单元绩效优化
丁祥海, 武历达
(杭州电子科技大学工业工程与管理研究所,浙江 杭州 310018)
考虑脑力负荷的自治装配单元绩效优化
丁祥海, 武历达
(杭州电子科技大学工业工程与管理研究所,浙江 杭州 310018)
摘要:针对脑力负荷过高导致产品质量低、脑力负荷过低导致生产效率低的问题,对自治装配单元中的绩效优化模式进行了研究.模式综合考虑质量和效率,以最佳绩效为目标,采用时间压力模型对脑力负荷进行建模,并考虑了操作者经验因素的影响.应用自适应惯性权重粒子群算法求解该模型,并通过实例验证了该模型可为自治装配单元的生产运作提供优化分析决策.
关键词:脑力负荷;自治装配单元;时间压力模型;粒子群算法
0引言
自治装配单元是指以手工装配为主,由轻巧易移动的低成本设施构成,致力于装配一种或几种产品并承担该产品大部分或全部装配工作的装配单元.在企业统一生产计划的前提下,自治装配单元的作业计划由工作人员(或工作团队)自主安排,工艺规划、生产计划、制造加工、质量保证等任务均在单元内部完成,物料和信息在单元内部高度集成.由于以手工操作为主,存在大量人因失误,造成单元绩效不稳定.在既定任务模式下,脑力负荷是影响人因失误的主要因素[1-2].工作站的复杂度也是自治装配单元中造成人因失误的主要因素之一[3].在考虑复杂性的前提下,脑力负荷维持在什么水平时自治装配系统的绩效最优,目前尚未见到这方面的相关研究.本文根据自治装配单元的特点,将复杂性分为选择复杂性(零件、夹具、工装、装配顺序的选择[4])、工艺复杂性(描述了装配操作的难易度)和设计复杂性(由装配件的组合方式和物理特性来衡量),并用基本装配时间和操作者对刺激状态做出的平均反映时间来描述复杂度[5],在此基础上构建了以质量(直通率)和效率(交货期)加权为多目标函数的最佳脑力负荷优化模型,给出了模型求解方法,通过实例对模型和方法进行了验证.
1问题建模
1.1自治装配单元的结构
工作站是自治装配单元的基本单元,工具、设备和物料都布局在工作站上,操作者的操作也在工作站内完成.自治装配单元可用集合J={1,2,…,j,…,n}表示,其中,j表示第j个工作站.在生产每个模块中需要一系列的物料,用Vj={Vj1,Vj2,…,VjLj}表示,其中Vjl(l=1,2,…,Lj)表示工作站j生产模块的第l个物料.用Nj表示操作者在每个工作站的装配操作动作数,包括物料、夹具、工装、装配程序等的选择任务和基本操作任务,其中用tj表示工作站j的操作动作中最少的时间.工作站j有Kj个选择操作活动,其中工作站j在进行第k个选择操作活动时,不仅受到工作站j其自身的物料影响,还有可能受到装配顺序在前的工作站的物料影响.
1.2脑力负荷的描述
脑力负荷通常被形容为操作员工在完成其目前工作的这段时间内由认知活动所引起的脑部资源的消耗量.现有数学模型很难精确地描述所有因素,“时间压力”模型已被证明与实际脑力负荷水平非常接近[6].工作站j的脑力负荷水平PMWLj用时间压力模型表示为:
PMWLj=(1-ρPELj)(TTSj+TTAj)/Tj..
(1)
其中,Tj表示工作站j的周期时间;TTAj表示工作站j的基本装配时间;TTSj表示工作站j的操作员工的平均反应时间;PELj(0≤PELj≤1)表示操作者的经验水平;ρ为操作者的经验水平对脑力负荷的影响系数.
由海曼(Hick-Hyman)定律,工作站j的操作员工的平均反应时间可描述为:
TTSj=aj+bjCCj.
(2)
其中,aj,bj表示对应的经验系数.
工作站j的选择复杂度CCj可描述为[7]:
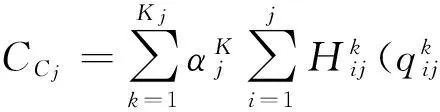
(3)
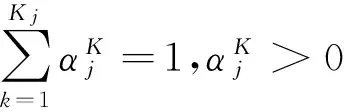
(4)
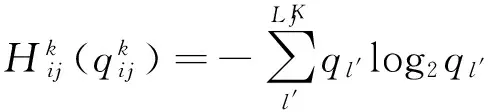
(5)
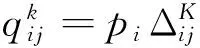
(6)
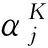
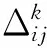
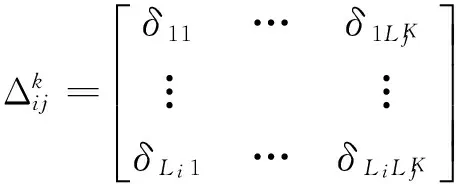
1.3绩效描述
串联布局是自治装配单元使用频率最高的布局方式[9],所以本文选择该布局方式开展研究.同时,选择质量和效率来描述单元的绩效.
1)质量的描述方法
直通率是指一次性合格率,在串联布局的生产线中可以通过将各个工作站的合格率相乘求得.在本文中用直通率来代表装配系统的质量,是1个无量纲的量.
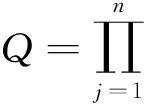
Qj=Yje-(PMWLj/θ)β.
(7)
其中,Yj表示只考虑复杂性的情况下,工作站j的一次合格率;θ,β分别为对应的尺度和形状参数.
Yj=Rje-NDPUj.
(8)
Rj=μ[1-e-γ(TTSj-δ)],
(9)
NDPUj=g(CTj,CDj),
(10)
CTj=TTAj-tjNj.
(11)
其中,NDPUj表示工作站所装配模块的单位缺陷数[10],Rj表示操作者的选择可靠性的概率[11];μ为调整选择可靠性的参数;γ表示一种敏感度参数,这里用来指反应时间对操作可靠性的敏感度;δ表示休整反应时间的参数;CTj表示工作站j的工艺复杂度,由Shibata模型可知;CDj表示工作站j的设计复杂度(设计复杂度可由专家打分所得;而函数g(CTj,CDj)是由关于设计复杂度和工艺复杂度直线回归函数求得;tj表示工作站j的最小装配动作时间,Nj表示工作站j的装配操作动作数.
2)效率描述方法
本文以交货期占计划生产时间的比率来表示效率的高低,即交货期越短效率越高,交货期越长效率越低.交货期可以用下面公式表示:
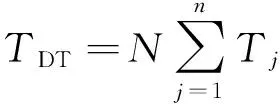
(12)
其中,N表示订单量,TDT表示交货期时间.
则效率PPE可以通过交货期占计划生产时间的比率来表示:
PPE=1-TDT/TPT+z..
(13)
其中,TPT表示订单计划生产时间,z表示效率调整因子.
3)绩效描述方法
通过对上述装配生产线脑力负荷对人因失误造成的问题进行分析,建立以最优脑力负荷为基础的产品生产直通率和效率的平衡数学模型.从质量的角度来说,装配产品追求的是最大的直通率.但是随着质量的单方面增加,操作者的耗时必随之增加,效率自然而然就会降低.故本文建立直通率与效率的双重优化函数,用加权法求最佳的系统绩效,最佳绩效对象的脑力负荷为最佳脑力负荷,表达式如下:
Maximize∶O=ω1Q+ω2PPE.
(14)
其中,ω1和ω2分别表示对直通率和效率赋予的权重,ω1+ω2=1,且ω1,ω2>0.
2算例验证
已知某自治装配单元生产电动工具产品,保证产能的最大生产时间是90s,该单元由3个工作站串联构成.工作站1生产的模块有3种物料类型,工作站2生产的模块有2种物料类型,工作站3生产的模块有3种物料类型.有1批订单,需要生产400个工具,限定在10h内交货.其装配布局如图1所示.
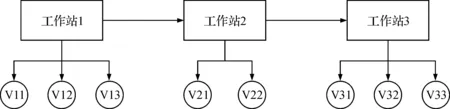
图1 自治装配单元中装配线结构布局图
每个工作站所对应生产模块的工艺复杂度由表1求出.

表1 工艺复杂度参数表
各个模块的设计复杂度先由专家对上述的设计复杂度参数打分,然后运用层次分析法对最终所得到的参数数据分析,以上3个模块的设计复杂度的最终结果为4.6,4.5和4.8.由上述可知,单位缺陷数NDUP可以通过工艺和设计复杂度用直线回归拟合[10],得出:
NDPUj=-6.691×10-4+1.786×10-5CDj+4.225×10-4CTj.
在每个工作站上须装配相应不同的物料,则3个工作站中物料混合需求的比率依次分别为[0.60.20.2],[0.50.5],[0.50.30.2].操作者在其对应的工作站进行装配工作时,需要进行以下4个选择任务:物料的选择、工具的选择、夹具的选择和装配程序的选择.其中,工作站间装配物料类型与选择活动的关系通过表2来表示.
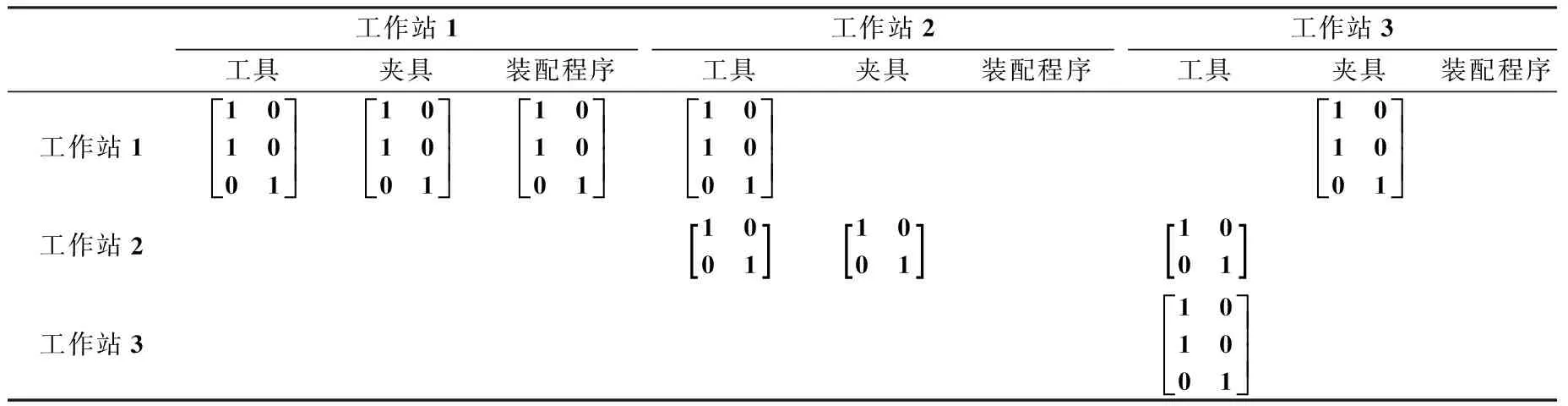
表2 工作站间装配物料类型与选择活动的关系
在此算例中,参数设定如下:所有工作站中的工具、夹具和装配程序的选择对选择复杂度的影响比重都是相同的,分别为0.4,0.4和0.2;式(1)中经验水平对脑力负荷的影响系数ρ为0.32;式(2)中的操作员工反应时间模型中参数a,b分别为0和1;式(7)中θ为1.2,β为5;式(9)中μ为1,γ为5,δ为0.2;式(13)中z为0.59.工作站所对应的操作员工的经验水平分别为0.7,0.65和0.75;目标函数式(14)中直通率和效率所占的权重ω1,ω2分别为0.6,0.4.
虽然标准粒子群优化算法(ParticleSwarmOptimization,PSO)可以有效地解决许多单目标优化问题,但是PSO易陷入局部最优解中.为了防止PSO算法无法取得全局最优解,本文选择自适应惯性权重粒子群优化算法来求解上述模型.取初始种群为40,为了更好地收敛于全局最优解,算法中的最大最小惯性权重分别取为0.9,0.6.种群规模被设定为(@fitness,40,2,2,0.9,0.6,200,3),通过自适应权重粒子群算200次迭代,求出目标函数最优时的结果,如表3所示.3个工作站的在目标函数取最优时的工作周期为81s,79s和82s,对应的脑力负荷分别为65.85%,66.26%和65.65%.此时的直通率Q为75.13%,交货期占计划期的比率为91.85%,即在规定的时间内提前完成订单.若自治装配单元在生产时不考虑脑力负荷对产品质量的影响,即Tj=TTAj+TTSj,此时3个工作站相应的脑力负荷分别为77.60%,79.20%和76.00%,且装配线的直通率为62.12%.

表3 考虑脑力负荷与不考虑脑力负荷的对比结果
在自治单元装配单元中,脑力负荷与绩效的关系图如图2所示,本文中假定最大脑力负荷工作站代表整条生产线的脑力负荷水平.
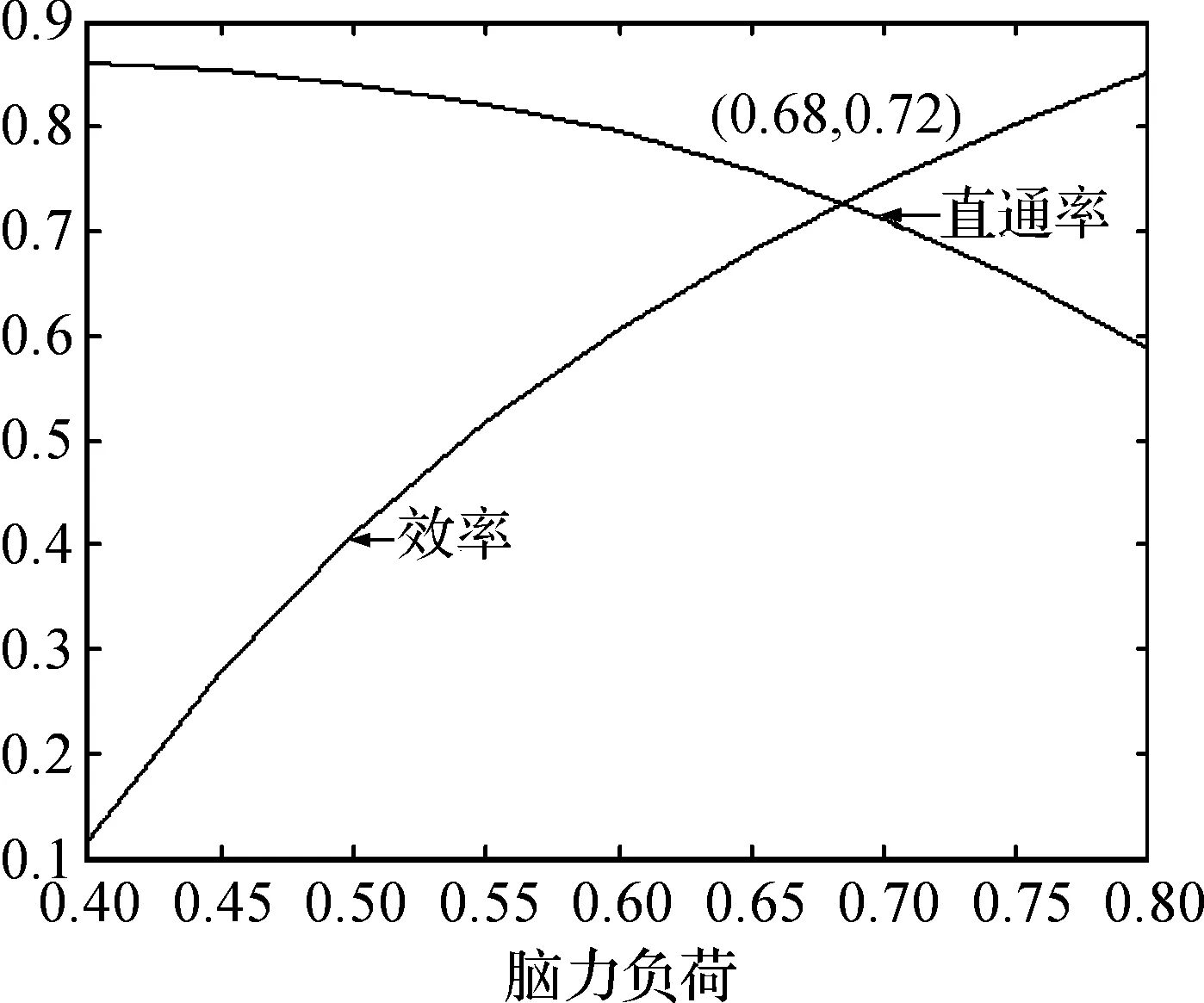
图2 脑力负荷与直通率和效率关系图
综上所述,在优化设计自治装配单元时,若不考虑脑力负荷对绩效的影响,直接采用基本装配时间和反应时之和作为工作站的周期时间,这种情况下,操作员工的脑力负荷处于较高水平.随着脑力负荷的增加,质量水平显著下降,即直通率随之降低.从生产图2脑力负荷与直通率和效率关系图的成本角度来讲,随着直通率的降低,报废的产品增加,对整个工厂的运营是非常不利的.
3结束语
本文考虑了工作站的基本装配时间、装配选择复杂性所引起的平均时间、操作者的脑力负荷以及操作者的经验水平,建立了考虑脑力负荷的自治装配单元的绩效优化模型.研究证明,保持适宜的脑力负荷能够提高自治装配单元的绩效.根据自治装配单元的现有信息,应用绩效优化模型可为其生产运作和优化设计提供决策支持.
参考文献
[1]ZHANGW.Causationmechanismofcoalminers’humanerrorsintheperspectiveoflifeevents[J].InternationalJournalofMiningScienceandTechnology,2014, 24(4): 581-586.
[2]明东,柯余峰,何峰,等.基于生理信号的脑力负荷检测及自适应自动化系统研究:40年回顾与最新进展[J].电子测量与仪器学报,2015,29(1):1-13.
[3]WALTERC,SCHMIDTS,ROSENSTIELW,etal.UsingCross-TaskClassificationforClassifyingWorkloadLevelsinComplexLearningTasks[C]//AffectiveComputingandIntelligentInteraction(ACII), 2013HumaineAssociationConferenceon.IEEE, 2013:876-881.
[4]ZHUX,HuSJ,KORENY.ModelingofManufacturingComplexityinMixed-ModelAssemblySystemsLines[J].JournalofManufacturingScience&Engineering, 2008, 130(5): 649-659.
[5]于新.变速箱装配线人因质量事故控制及其复杂性研究[D].长春:吉林大学,2011.
[6]廖建桥.脑力负荷的预测与分析方法[J].工业工程.1998,1(1):38-42.
[7]饶运清.基于信息熵的制造系统复杂性测度及其在调度中的应用[J].机械工程学报,2006,42(7):8-13.
[8]李莉.基于脑力负荷的混流装配产品质量与效率平衡优化研究[D].天津:天津大学,2014.
[9]于瑞峰,王永县.手工装配作业单元的布局优化设计研究[J].工业工程与管理,2004,2(2):36-39.
[10]窦惠婷,苏强,陶文昊.汽车发动机装配过程中人为缺陷预测研究[J].工业工程与管理,2013(1):129-134.
[11]YANGM,GAOJ,ZHAOB,etal.Studyofoperatorreliabilityinnuclearpowerplants[J].Chinesesciencebulletin, 1997, 42(19): 1585-1590.
Study on the Performance Optimization of Autonomous Assembly Unit Based on the Mental Workload
DING Xianghai, WU Lida
(InstituteofIndustrialEngineering,HangzhouDianziUniversity,HangzhouZhejiang310018,China)
Abstract:According to the mental workload was too high, which led to low quality of the products and the mental workload was too low lead to the problem of low production efficiency, performance of autonomous assembly unit optimization model was studied. By considering the influence of operator experience, time pressure model to mental workload was established for quality and efficiency of production units trying to take the best performance as the target. Adaptive weight particle swarm optimization algorithm was applied to solve the model and the example of a practical problem was applied to verify the model which can provide the optimal analysis and decision for the production and operation of the autonomous assembly unit.
Key words:mental workload; autonomous assembly unit; the time pressure model; particle swarm optimization
DOI:10.13954/j.cnki.hdu.2016.04.021
收稿日期:2015-11-30
基金项目:浙江省自然科学基金资助项目(LY13G010007)
作者简介:丁祥海(1971-),男,湖南湘潭人,副教授,工业工程.
中图分类号:TH186
文献标识码:A
文章编号:1001-9146(2016)04-0098-05

