修正的Stancu型q-Baskakov-Shurder-Szász算子的逼近
吴华亭,胡晓敏
(杭州电子科技大学数学研究所,浙江 杭州 310018)
修正的Stancu型q-Baskakov-Shurder-Szász算子的逼近
吴华亭,胡晓敏
(杭州电子科技大学数学研究所,浙江 杭州 310018)
摘要:研究了一类修正的Stancu型q-Baskakov-Shurder-Szász算子的逼近性质,给出了加权空间下的逼近,通过光滑模下的加权空间给出该类算子的误差估计.利用K-泛函和光滑模给出了这类算子的一些逼近性质.最后,运用King型定理优化了误差估计并得到优化后的加权估计.
关键词:修正;逼近;K-泛函;光滑模
0引言
近年来,随着q-整数的发展,其在逼近论中的应用也越来越广泛,成为该领域中的一个研究热点.越来越多的专家学者投入到对q-整数的不同算子的逼近研究中,并取得了许多结果[1-5].文献[1]和文献[2]分别介绍了Durrmeyer型修正的q-Baskakov算子和单纯型q-Baskakov算子的逼近性质,文献[3]得到了q型Szász-Beta算子的逼近收敛性质,文献[4]则是在文献[2]的基础上研究了广义的q-Baskakov算子的逼近性质,文献[5]介绍了q-Baskakov-Szász算子的逼近收敛性质.本文在文献[6]的基础上进行修正,得到了一种新的q-Baskakov-Shurder-Szász算子的形式,修正后的算子既常数保持又线性保持.本文在修正后的这一类算子的基础上,研究了其stancu型的逼近性质,并运用King型定理进行了优化,对于探究该类修正的q-Baskakov-Shurder-Szász算子的逼近等性质有一定的研究意义.
1相关定义及引理
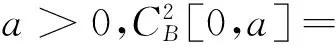
定义1设f是区间[0,∞)上的实值连续函数,p,k∈N,n∈N{0},A>0,得到修正的q-Baskakov-Shurder-Szász算子:
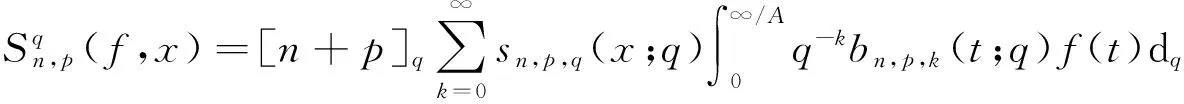
(1)
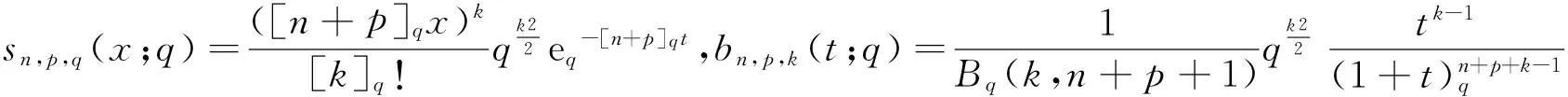
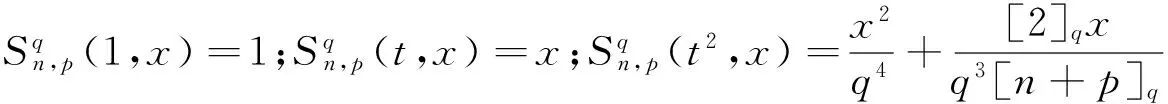
定义2设f是区间[0,∞)上的实值连续函数,p,k∈N,n∈∞{0},A>0,定义stancu型的q-Baskakov-Shurder-Szász算子为:
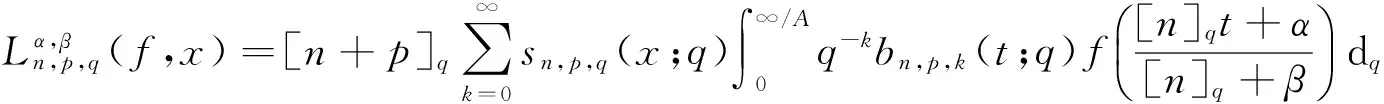
(2)
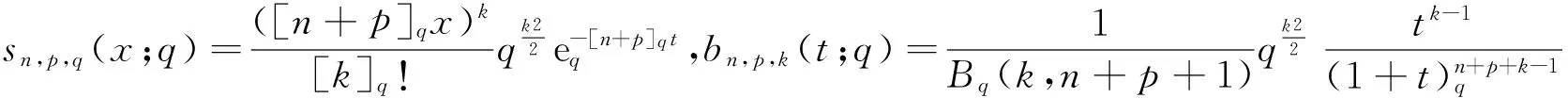
由引理1得出:
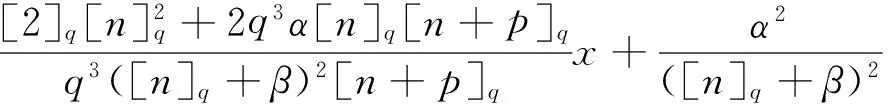
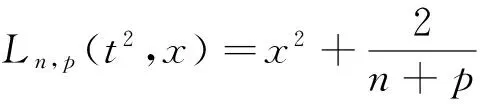
注2由引理2易得:
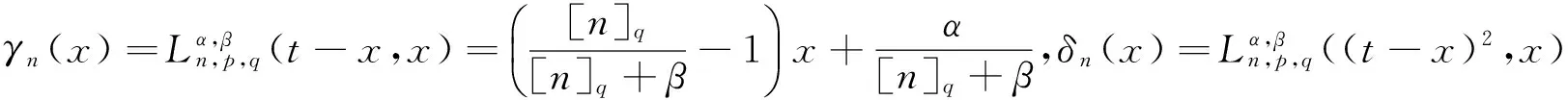
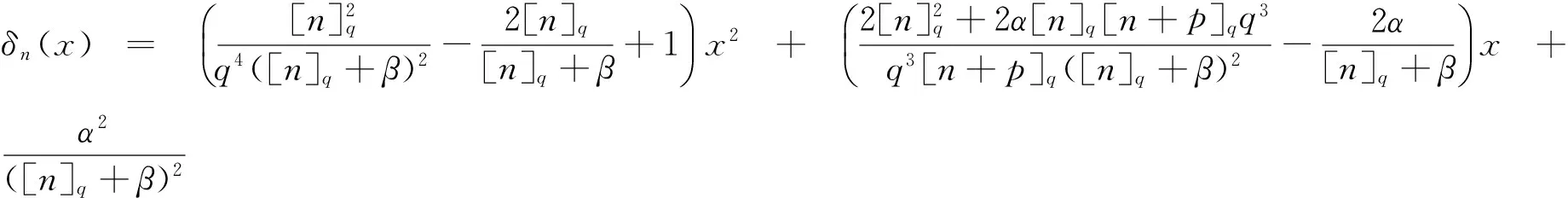

预计全年原油表观消费量约6.33亿吨,同比增长4.5%;天然气表观消费量约2810亿立方米,增幅17.5%;成品油表观消费量约3.27亿吨,增长2%,其中柴油表观消费量约1.67亿吨,与上年大致持平;化肥表观消费量约4780万吨(折纯),下降4%,其中尿素表观消费量约为2220万吨,降幅6%;合成树脂表观消费量约1.12亿吨,增长4.5%;乙烯表观消费量约2085万吨,增长3%;烧碱表观消费量约3215万吨,增幅2.5%。
2主要定理
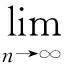
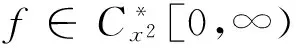
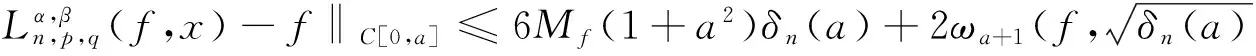
证明只需证:
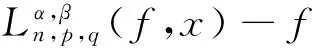
(3)
对所有的(x,t)∈[0,a]×[0,∞)∶S,记:S=S1∪S2∶={(x,t)∶0≤x≤a,0≤t≤a+1}∪{(x,t)∶0≤x≤a,t>a+1}.
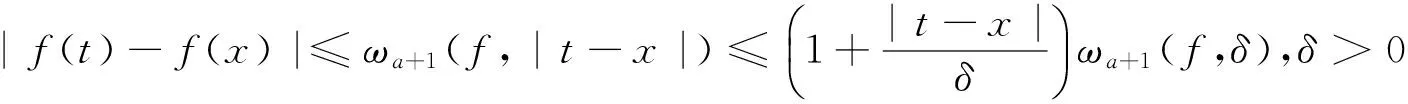
(4)
|f(t)-f(x)|≤Mf(1+x2+t2)≤Mf(1+3x2+2(t-x)2)≤6Mf(1+a2)(t-x)2.
(5)
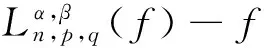
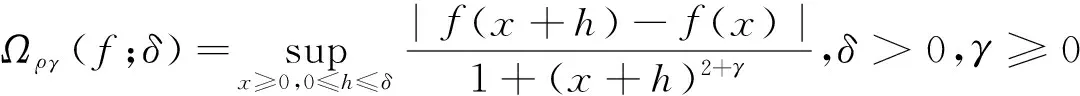
(6)
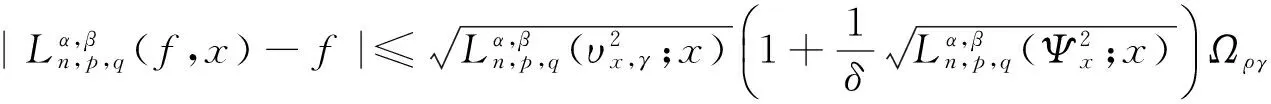
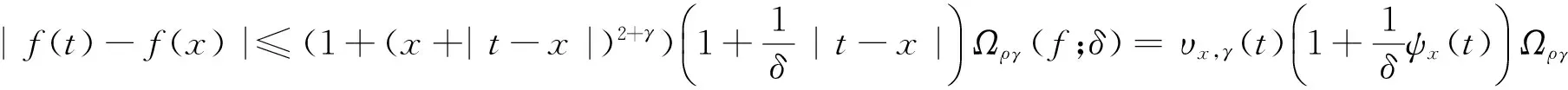
(7)
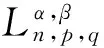
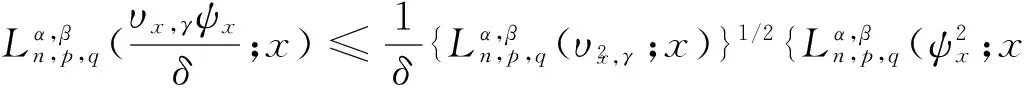
(8)
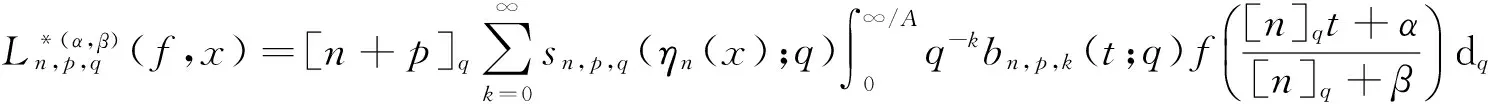
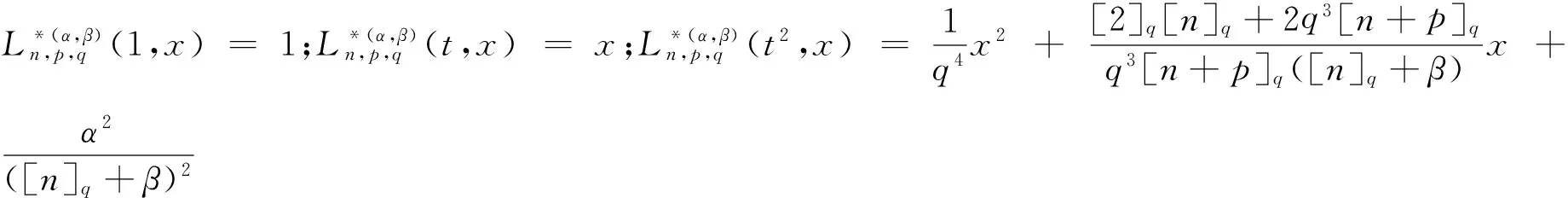
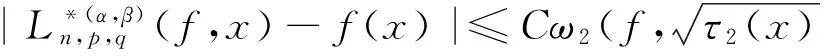
证明方法与定理3相同.
3结束语
本文在文献[6]的基础上进行q型Baskakov-Shurder-Szász算子的修正,得到了一种新的Stancu型q-Baskakov-Shurder-Szász算子的形式,研究了该类算子的各阶矩和中心矩的误差估计和逼近性质,并运用King型定理对该类算子进行了优化,拓展了对一般q型算子的认识.本文没有对该类算子进行加权统计收敛性质研究,将对该类问题进行进一步探讨.
参考文献
[1]ARAL A, GUPTA V. On the Durrmeyer type modification of the q-Baskakov type operators[J].Nonlinear Analysis: Theory, Methods & Applications, 2010, 72(3): 1171-1180.
[2]ARAL A, GUPTA V. On q-Baskakov Type Operators[J]. Demonstratio Mathematica, 2009, 42(1): 109-122.
[3]GUPTA V, ARAL A. Convergence of the q analogue of Szász-Beta operators[J]. Applied Mathematics and Computation, 2010, 216(2): 374-380.
[4]ARAL A, GUPTA V. Generalized q-Baskakov Operators[J]. Mathematica Slovaca, 2011, 61(4): 619-639.
[5]GUPTA V. A note on q-Baskakov-Szász operators[J]. Lobachevskii Journal of Mathematics, 2010, 31(4): 359-366.
[7]DITZIAN Z, TOTIK V. Moduli of Smoothness[M]. New York: Springer-Verlag, 1987: 10-23, 159-175.
[8]KING J P. Positive linear operators which preserve x2[J]. Acta Mathematica Hungarica, 2003, 99(3): 203-208.
Approximation Properties of Modified q-Baskakov-Shurder-Szász of Stancu Type Operators
WU Huating, HU Xiaomin
(InstituteofMathematics,HangzhouDianziUniversity,HangzhouZhejiang310018,China)
Abstract:In this paper, we are dealing with a new type of Stancu type modified q-Baskakov-Schurder-Szász operators. We give some errors estimations by using a weighted modulus of smoothness associated to the weighted space. The rate of convergence in terms of usual moduli of smoothness is given, and investigated the convergence in certain weighed spaces. We also give better error estimations for the operators using King type approach and obtained weighted approximation properties.
Key words:modified; approximation; Peetre’s K-functional; modulus of smoothness
DOI:10.13954/j.cnki.hdu.2016.04.020
收稿日期:2015-11-30
作者简介:吴华亭(1992-),女,河南濮阳人,硕士研究生,函数逼近论.通信作者:胡晓敏副教授:E-mail:mathhuxm@163.com.
中图分类号:O174.41
文献标识码:A
文章编号:1001-9146(2016)04-0094-04

