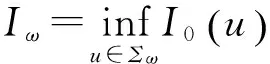一维向列相液晶模型方程孤立波解的存在性

张真真,　章国庆

(上海理工大学 理学院,上海　200093)



一维向列相液晶模型方程孤立波解的存在性

张真真,章国庆

(上海理工大学 理学院,上海200093)

摘要：在证明W1,2(-∞,+∞)空间中向列相液晶模型方程孤立波解的存在性的过程中,关键是要证明相关的泛函是紧性的.因此,首先可根据临界点理论中的集中紧性原理的方法,证明二分性以及消失性不成立,即在W1,2(-∞, +∞)空间中泛函的极小化序列的紧性是成立的,进一步利用极值原理的方法,得到一维向列相液晶模型方程孤立波解的存在性.

关键词：向列相液晶模型方程组; 能量极小孤立波解; 存在性

1问题的提出

本文研究如下一维向列相液晶模型方程组

(1)

其中,m>0为常数.令E(x,z)=eiλzu(x),z>0,λ∈,代入问题(1),则问题(1)的孤立波解满足

(2)

近年来,由于向列相液晶的非线性与非局部的特性产生了许多有意义的物理现象,因此,问题(2)深受许多学者的关注.2003年,Assanto等[1]发现空间向列相液晶的孤立波是稳定的; 在文献[2-5]中,实验和理论计算都表明空间孤立波都能在非局部向列相液晶中稳定地传播;Peccianti等[6]综述了在向列相液晶中孤立波解的最新进展;Panayotaros等[7]研究了二维向列相液晶中孤立波解的存在性及其对称性;Bellazzini等[8]和Georgiev等[9]也研究了m=0时问题(2)在三维空间上基态解的存在性以及对称性.

对于问题(2),当m=0时,文献[10]研究了基态解的存在性和唯一性,但问题(2)的第二个方程对应为Coulomb位势;当m≠0时,问题(2)的第二个方程对应为Yukawa位势[11].本文主要利用临界点理论中集中紧性原理和极值问题来证明问题(1)能量极小孤立波解的存在性.

2预备知识和主要结论

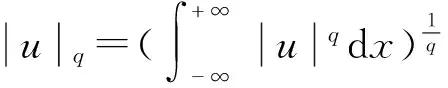
以及相应的范数为

由问题(2)的第二个方程可得

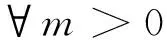
(3)

将式(3)代入问题(2)中的第一个方程可得如下非线性非局部问题

(4)

因此,求解方程(4)等价于求解问题(2).现考虑如下泛函

引理1泛函V(u),I(u)在W1,2(-∞,+∞)上是一阶连续可微的.

证明令{un}⊂W1,2(-∞,+∞)且un→u,其中,u∈W1,2(-∞,+∞),则序列{un}是有界的且

其中,C>0是常数.因此,当n→∞时,有V(un)→V(u).对于∀u,v∈W1,2(-∞,+∞),可得

其中

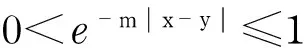
其中,C0,C,C1>0为常数.显然

令

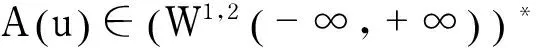
其中,C0,C,C1,C2>0为常数.因此,泛函V(u)是一阶连续可微的,且

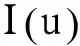
其中,∀u,v∈W1,2(-∞,+∞).因此,泛函I(u)的临界点即为问题(4)的弱解.

现考虑如下极小值问题

其中

以及

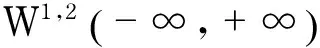
本文的主要结果为:

定理1对于任意m>0,问题(2)存在能量极小孤立波解u,且u是正的、径向对称以及严格递减的.

3主要结果的证明

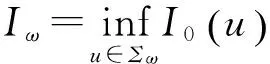
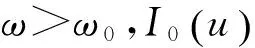
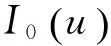
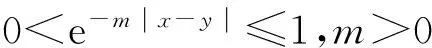
其中,C为常数.据u∈Σω,可得

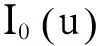
引理3对任意的m>0,存在ω0>0,使得

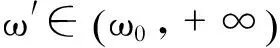
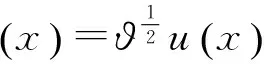
以及

因此,可得

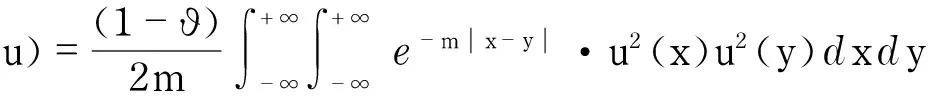
从而引理3得证.

断言1现用反证法,假设消失性成立,则

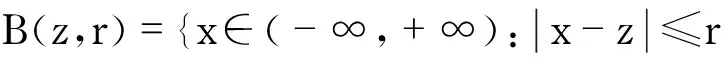
由引理2可得,序列{un}在W1,2(-∞,+∞)上是有界的.因此,由Lions引理可得,在Ls(-∞,+∞)(s>2)中,un→0,则由Hölder不等式有

从而可得,Iω≥0.由引理3知,当ω充分大时,在Σω上Iω<0,故得出矛盾,即消失性不成立.

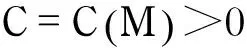
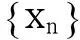
选取序列Rn→∞,且当n充分大时,Rn≥R且满足

定义

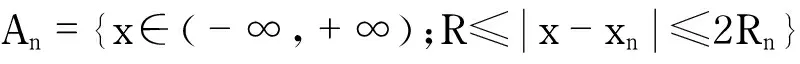
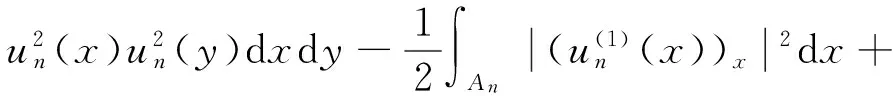
以及

其中,当ε→0时,δ(ε)→0.因此,当n→∞时,成立

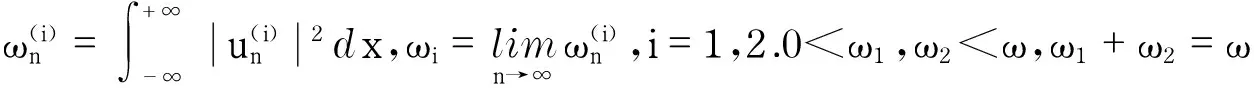
(7)

因为

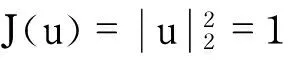
因此,

故可得Iω

综合断言1以及断言2可知,I0(u)在Σω中的极小化序列{un}在Σω上是相对紧的.

即u为问题(4)的弱解.

类似于文献[7]中引理4.8以及引理4.9的证明,可得u>0,且是径向对称以及严格递减的,即问题(2)存在能量极小孤立波解.

参考文献：

[1]ASSANTO G,PECCIANTI M,CONTI C.Nematicons:optical spatial solitons in nematic liquid crystals[J].Optics and Photonics News,2003,14(2):44-48.

[2]HENNINOT J F,BLACH J F,WARENGHEM M.Experimental study of the nonlocality of spatial optical solitons excited in nematic liquid crystal[J].Journal of Optics A:Pure and Applied Optics,2007,9(1):20-25.

[3]ASSANTO G,MINZONI A A,PECCIANTI M,et al.Optical solitary waves escaping a wide trapping potential in nematic liquid crystals:modulation theory[J].Physical Review A,2009,79(3):033837.

[4]ALBERUCCI A,PICCARDI A,PECCIANTI M,et al.Propagation of spatial optical solitons in a dielectric with adjustable nonlinearity[J].Physical Review A,2010,82(2):023806.

[5]CONTI C,PECCIANTI M,ASSANTO G.Route to nonlocality and observation of accessible solitons[J].Physical Review Letters,2003,91(7):073901.

[6]PECCIANTI M,ASSANTO G.Nematicons[J].Physics Reports,2012,516(4/5):147-208.

[7]PANAYOTAROS P,MARCHANT T R.Solitary waves in nematic liquid crystals[J].Physica D:Nonlinear Phenomena,2014,268:106-117.

[8]BELLAZZINI J,SICILIANO G.Stable standing waves for a class of nonlinear Schrödinger-Poisson equations[J].Zeitschrift für Angewandte Mathematik und Physik,2011,62(2):267-280.

[9]GEORGIEV V,PRINARI F,VISCIGLIA N.On the radiality of constrained minimizers to the Schrödinger-Poisson-Slater energy[J].Annales de L’Institut Henri Poincare(C)Non Linear Analysis,2012,29(3):369-376.

[10]CHOQUARD P,STUBBE J.The one-dimensional Schrödinger-Newton equations[J].Letters in Mathematical Physics,2007,81(2):177-184.

[11]LIED E H,LOSS M.分析学[M].王斯蕾,译.2版.北京:高等教育出版社,2007.

[12]LIONS P L.The concentration-compactness principle in the calculus of variations,the locally compact case,part I[J].Annales de L’Institut Henri Poincaré-Aanalyse Non Linéaire,1984,1(2):109-145.

(编辑:丁红艺)

Existence of Solitary Wave Solutions for One-dimensional Nematic Liquid Crystals Model Equations

ZHANG Zhenzhen,ZHANG Guoqing

(College of Science,University of Shanghai for Science and Technology,Shanghai 200093,China)

Abstract：In the process of proving the existence of solitary wave solutions for one-dimensional nematic liquid crystal model equations in W1,2(-∞,+∞), the key point is to prove that the relevant functional is compact.Therefore,firstly,using the method of concentrated-compactness principle in the critical points theory,two bad cases:dichotomy and vanishing were eliminated,and prove the compactness of the minimizing sequences was proved.Then,the existence of solitary wave solutions for one-dimensional nematic liquid crystal model equations was obtained by using the extremum principle.

Keywords：nematic liquid crystals model equations; energy minimizing solitary wave solution; existence

文章编号：1007-6735(2016)03-0218-05

DOI：10.13255/j.cnki.jusst.2016.03.003

收稿日期：2015-07-20

基金项目：上海市自然科学基金资助项目(15ZR1429500);沪江基金资助项目(B14005)

通信作者：章国庆(1973-),男,副教授.研究方向:非线性泛函分析.E-mail:745826192@qq.com

中图分类号：O 175.25

文献标志码：A

第一作者： 张真真(1989-),女,硕士研究生.研究方向:非线性泛函分析.E-mail:1215934987@qq.com