初中生学习数学的兴趣培养

沈志明

兴趣是最好的老师，当我们对一件事有兴趣的时候，会不由自主地关注它，想方设法地了解它，自觉主动地探究它。兴趣甚至能让人废寝忘食。激发学生对学习数学产生兴趣，直接关系到学生学习数学的效果。数学的抽象性往往使学生对它望而生畏，它不像其他自然科学容易引起学生的兴趣。有时老师缺少分析或不当讲述还会让学生感觉“学数学真难，我没这个天分”的挫败感；而低效甚至无效的自主探究，也常因难以体验成功的喜悦而使学生逐渐丧失信心，继而失去学习兴趣。初中阶段如何培养学生学习数学的兴趣，下面笔者就自身的实践谈谈看法。

一、处理好直观与抽象的关系

初中生正处于形象思维和抽象思维的过渡阶段，直观具体和形象的事物学生较易接受。教学中应注意以形助数，数形结合，或结合生活中的实例，使问题具体化，使学生易于理解接受。对自主探究，能体验探究且有所获，学生才会对探究活动产生兴趣。要做到这点，首先，课程内容要贴近生活、贴近学生实际。如用“一只青蛙一张嘴、两只眼睛四条腿……”探索具体问题中的数量关系和变化规律。又如利用生活中的轴对称现象，引导学生欣赏身边的轴对称图形，观察枫叶、蝴蝶等图片，用自己的语言描述图形的特点，既能体验从具体情境中抽象出数学符号的过程，又能唤起学生学习数学的兴趣。其次，应引到学生学会应用“特殊到一般”的思想分析解决问题。如问题：k为任意常数、试证直线y=（k+1）x-k-1恒过某一定点。初中生对带参变量的直线经常头痛，一些学生观察关系式便可知直线必过定点（1，0），大部分学生会茫然不知所措。此时，可引导学生，既然y=（k+1）x-k-1对任何k都成立，则任取K的两个具体值所得的两条确定直线必过定点，从而通过解方程组也可得到定点。通过抽象问题具体化使不同的人在数学上得到不同的发展。

二、引导学生学会“转化”体验“获取”知识快乐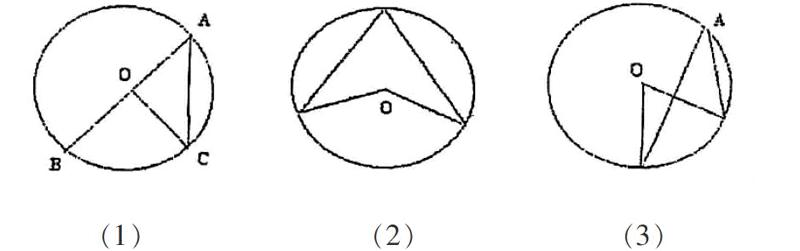

数学知识往往环环相扣，新旧知识间总存在联系，学生如何在已有的知识基础上，将新的知识内化为自己的知识，形成新的知识体系，最基本也最有效的方法是“转化”。例如，因式分解与整式乘法是互逆的关系，学生有了整式乘法的知识后，只要给出分解因式定义，便可引导学生逆用分配律m（a+b+c）=ma+mb+mc，获得因式分解方法——提取公因式法；观察乘法公式特征，逆用乘法公式即可获取因式分解的另一种方法——运用公式法。又如，学生有了解一元一次方程的经验后，可引导学生利用等式的性质将分式方程转化为整式方程；对二元一次方程组的求解问题可引导学生通过“代入消元”或“加减消元”将多元转化成一元、利用公式=|a|=a a≥0-a a<0可将求算术根问题转化为求绝对值问题……

自主探究是学习数学的重要方式，帮助学生进行有效探究的途径是以旧引新，实现新旧知识的转化。获得感和成就感能不断提高学生学习数学的兴趣。

三、教学要符合学生的认知规律，探求知识应由简到繁

譬如，对一元二次方程求解问题，可先从最简形式x=a入手，因方程x=a的求解问题换一个角度可看成求平方根问题，从而转化成学生熟悉的、已掌握的问题，进而引导学生探求方程（x+a）=c的根，此时只要将（x+a）看成新“元”，利用换元法即可转化为已解决的问题。最后对一般方程ax+bx+c=0（a=0）解的探求，可引导学生通过配方法转化为（x+a）=c的求根问题，进而引导出求根公式，从而彻底解决一元二次方程的求根问题。类似地，探索二次函数知识时，可从最简函数y=x入手，通过描点作图，获取函数性质后，左、右平移可探得y=（x+a）的图像和性质，上、下平移可探得y=x+h的图像性质，利用平移性质掌握了y=（x-h）+k的图像和性质，有了基础，再探索一般形式二次函数y=ax+bx+c问题，只需利用配方法将一般式化成y=a（x-h）+k即可使问题迎刃而解。

四、前瞻性引导，让学生少走弯路

学生探索知识犹如初次登山，虽有目标，但不熟悉途径，往往多走弯路，教师则由于已登顶峰，居高临下，更能看清来路。如，学生分解因式x-x总犯分解不彻底的错误：x-x=x（x-1）。为避免学生分解不彻底问题，教学分解因式定义“把一多项式化成几个整式的积的形式，这种变形叫做把这个多项式分解因式”时，可引导学生将“因式分解，必须分解到每一项都不能分解为止”作为定义的一部分，加以理解应用。这样，学生因分解不彻底而产生错误的概率就大为减少。又如当不等式组x2m-1无解，求m的取值范围，学生往往记得口诀“大于大、小于小”不等式组无解，从而得出错解：由2m-1>m+1得m>2。为避免错误，可先设计问题：不等式组x>3x<3有解吗？通过特例记住不等式组无解的所有情况。

五、优化探究问题的设计，让学生乐此不疲

学生自主探索是否有效，与教师对探究过程的充分考虑有关。要使学生体验发现的乐趣，必要的铺垫设计是前提。以圆周角定理探索为例，让学生从纷繁的圆周角中发现定理的结论，可设计如下问题串，将学生一步一步引向成功。

问题一：圆周角与圆心的位置关系有几种情况？引导学生观察图（1）、（2）、（3）得出结论：以圆上任意一点为顶点的圆周角，虽然有无数多个，但它们与圆心的位置关系却有三种：

问题二：圆周角与圆心角虽是不同的角，但是只要它们对着同一条弧，彼此之间就有着一定的关系。那么圆周角与对同一条弧的圆心角之间有什么关系呢？

可引导学生观察图（1）、（2）、（3），凭直觉猜想，动手测量，从特殊情况入手（特殊位置往往能得到特别的结论）。由图（1）学生不难发现：当圆心在角的一边上时，一条弧所对的圆周角等于它所对圆心角的一半。

问题三：仅由图（1）得出的结论能否得到“一条弧所对的圆周角等于它所对的圆心角的一半”？

问题四：能否通过作适当的辅助线把图（2）、（3）情况转化成图（1）情况？

利用（1）得出的结论，学生不难发现，当圆心在角的内部、外部时，结论仍然成立。此时，可引导学生将所发现的事实概括成定理，还可顺藤摸瓜，扩大成果。

问题五：半圆是不是弧，当圆周角是直角，或弧为半圆时，由圆周角定理可得什么结论？

总之，只有充分了解初中生的年龄特征，遵从学生的认知规律，精心设计学生的探索途径，才能使学生多体验成功少感受挫折，才能激发学生的学习热情，培养学生的学习兴趣。