基于DBN,SVM和BP神经网络的光谱分类比较
李俊峰,汪月乐,胡 升,何慧灵*
1. 三峡大学计算机与信息学院,湖北 宜昌 443002
2. 三峡大学理学院,湖北 宜昌 443002
基于DBN,SVM和BP神经网络的光谱分类比较
李俊峰1,汪月乐1,胡 升2,何慧灵2*
1. 三峡大学计算机与信息学院,湖北 宜昌 443002
2. 三峡大学理学院,湖北 宜昌 443002
恒星的分类对了解恒星和星系形成与演化历史具有重要的研究价值。面对大型巡天计划及由此产生的海量数据,如何迅速准确地将天体自动分类显得尤为重要。通过对SDSS DR9的恒星光谱数据进行深度置信神经网络(DBN)、神经网络和支持向量机(SVM)等算法分类的对比,分析三种自动光谱分类方法在恒星分类上的适用性。首先利用上述三种方法对K,F恒星进行识别分类,然后再分别对K1,K3和K5次型和F2,F5,F9次型识别,最后基于SVM支持向量机的二次分类模型,利用K次型的数据,构建剔除不属于K次型的模型。结果表明:深度置信网络对K,F型恒星分类效果较好,但是对K,F次型的分类效果不佳;SVM支持向量机在K,F型恒星分类以及相应的次型分类都具有较好的识别率,对K,F型分类效果要好于K,F次型的分类效果;BP神经网络对K,F型恒星以及其次型的识别一般;在剔除不属于K次型实验中,剔除率高达100%,可知SVM能够对未知的光谱数据进行筛选与分类。
深度置信网络;BP神经网络;SVM支持向量机;光谱自动
引 言
随着天文观测技术的不断改进,获取数据能力的提升和大型光谱巡天计划的实施,天体光谱数据的自动处理研究越来越受到重视和关注[1]。恒星的分类是天文学的基本分类任务之一,主要是根据恒星在不同波段的表现性质的不同,应用不同的方法将它们各自区分开来。恒星的分类对了解恒星和星系形成与演化历史具有重要的研究价值。面对大型巡天计划及由此产生的海量数据,如何迅速准确地将天体自动分类显得尤为重要。通过深度置信神经网络(deep belief network,DBN)自动分类方法[2-4],神经网络(back-propagation, BP)和支持向量机(support vector machine, SVM)[5-6]对恒星光谱进行了分类。
目前,已经有很多研究者在恒星分类上进行了研究。例如:Ball, Nicholas M等[7]的利用决策树对斯隆数字巡天DR3的数据进行星系分类。Banerji, Manda等[8]的Galaxy Zoo: 利用人工神经网络对DR6的星系数据进行了分类。严太生等[9]的基于自动聚类的算法的恒星/星系分类,对SDSS DR6的恒星/星系的测光数据进行了分析,恒星识别率高达98.52%。刘忠宝等的流形判别分析和支持向量机的恒星光谱数据自动分类方法,对SDSS的光谱数据进行了分类,也得到了较好的结果。屠良平等的基于局部均值的K-近质心近邻光谱分析,对SDSS DR8光谱数据进行了分类,其中恒星的识别率达到了98.9%。其他光谱分类上也有大量的研究。李乡儒等的RVM有监督特征提取对Seyfert光谱的分类。杨金福等利用核覆盖算法对星系和类星体的分类。赵梅芳等的利用自适应增强的方法对活动星系核的分类。
本文通过DBN,BP神经网络和SVM对SDSS DR9的恒星测光数据进行分析处理,比较三种方法在K型、F型恒星光谱分类上的差别,特别对于少有文献报道的光谱次型分类和未知光谱的分类方面做了相关研究。结果表明:SVM在K,F的次型分类方面明显优于DBN与BP神经网络方法。
1 模型介绍
1.1 深度置信网络(DBN)
1.1.1 深度置信网络介绍
深度置信神经网络(DBN)是一种无监督学习下的机器学习模型,它由N个受限制的玻尔兹曼机单元构成。Boltzmann机是基于能量的概率模型,概率分布模型为
(1)
玻尔兹曼机由可见层v与隐层h构成的无向图模型(同层的节点之间无连接),其能量函数为
(2)
其中,E为h,θ={Wij,bi,cj}的函数;bi,cj分别为可见单元i的偏置和隐层单元j的偏置;Wij为可见单元i与隐层单元j的连接权重;vi,hj分别为单元i与隐层单元j的各个节点的值。
1.1.2 学习算法
无监督的贪婪算法将采用自底朝上的顺序,分层对DBN进行无监督学习。具体算法如下:
Step1: 以x=h0为外界输入,训练第一层的RBM使其达到能量平衡;
Step2: 将第一层训练得到的联合分布,作为第二层的RBM的输入;
Step3: 重复Step2,直至最后一层。
Step4: 精调网络各层参数
1.2 BP神经网络介绍
BP神经网络是一种有监督的机器学习方法,旨在反映人脑结构及功能的一种抽象数学模型。
(1)计算各单元输出层的实际输出值yi
(3)
其中wij输入层第i单元与隐层第j单元的连接权重,θj隐层第j单元阈值。
(2)计算各单元输出层的实际输出值yt
(4)
(3)设定误差参数
(5)
(4)计算输出层的各单元的调整误差δt
(6)
(5)调整反向修正各层权值w和阈值θ
(7)
(8)
c为动量因子,η为学习率。
1.3 支持向量机(SVM)
1.3.1 支持向量机(SVM)介绍
支持向量机的学习目标就是构建一个决策函数,将数据正确分类。学习目标函数如下
(9)
其中,C为惩罚参数。
采用Lagrange乘子法求解式(9)。具有线性约束的二次规划问题,对应的对偶问题为
(10)
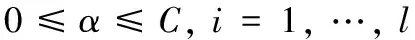
其中,K为核函数,其中不为0的αi所对应的样本为支持向量机。最后得出判别函数。
1.3.2 学习算法
Step1: 将大型的QP问题转化为一系列规模较小的QP问题;
Step2: 找到所有的非零的Lagrange乘数并删除;
Step3: 将上一个剩的具有非零的Lagrange乘数样本以及M个不满足KKT条件的的最差样本作为下一个QP问题的样本;
Step4: 如果在某一子QP问题中,不满足KKT条件的样本数不足M个,则这些样本全部加入到新的QP问题中;
Step5: 所有非零Lagrange乘数都被找到,从而解决了初始的大型QP问题。
1.3.3 二叉树型支持向量机多类分类器
如图1:二叉树型支持向量机的基本思想是从根节点开始,采取某种方法将该节点所包含的类别划分为两个子类,然后再对两个子类进一步划分,如此循环,直到子类中只包含一个类别。

图1 二叉树型支持向量机
2 光谱分类
2.1 对K,F型光谱的分类
选择了SDSS DR9中K,F光谱数据作为实验样本库。且每类光谱的数据量为15 000条。每条光谱均匀采样3 800个点,并采用对数波长数据格式。为使分类器有效的识别两种类型,需保持两个样本的训练集数量的均衡。DBN训练集数据为F,K型各4 900条;SVM训练集数据为F,K型各1 500条;BP神经网络训练集数据为F,K型各2 500条。分别从样本库中随机抽取测试集,剩下的作为测试集。且为了使实验具有统计的意义,实验独立重复10次。然后将数据归一化,利用深度置信网络训练、BP神经网络和SVM支持向量机进行光谱的分类并对比,最后利用测试集来检测分类的准确。实验结果如表1所示。
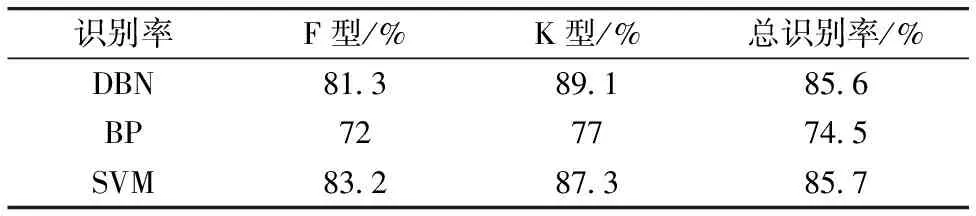
表1 K,F型的分类结果
2.2 次型光谱分类
该实验分为两个独立的实验,实验数据仍以SDSS DR9中光谱数据作为实验样本库。K次型光谱分类数据:DBN训练集数据为K1,K3,K5型各4 000条;SVM训练集数据为K1,K3,K5型各2 000条;BP神经网络训练集数据为K1,K3,K5型各2 500条。分别从样本库中随机抽取测试集,剩下的作为测试集,独立重复10次。F次型光谱分类数据:DBN训练集数据为F2,F5,F9型各4 000条;SVM训练集数据为F2,F5,F9型各4 000条;BP神经网络训练集数据为F2,F5,F9型各2 500条。分别从样本库中随机抽取测试集,剩下的作为测试集,独立重复10次。实验结果如表2所示。
2.3 基于SVM的剔除不属于K次型分类器
介于目前的分类器只能对其训练的类别进行分类,这里提出利用“一对多”分类思想,基于SVM支持向量机的二次分类模型,利用K次型的数据,构建剔除不属于K次型的模型。并利用2 000条G型光谱和2 000条F型光谱数据做了分类器的剔除不属于K次型的实验,结果如表3所示。

表3 排除率
3 结果分析
由表1表明:在恒星K,F型光谱分类上SVM与DBN方法的识别率分别为85.6%,85.7%。两种方法的识别率相差不大。但与BP神经网络对比结果可知,DBN和SVM的在恒星分类效果明显好于传统的BP神经网络。DBN和SVM对K,F型光谱的分类更具有效性。但是DBN和SVM的总的识别率都不是特别的高,这也反映了在F,K型分类上两个方法确实有其局限性。由表2表明:SVM在恒星次型的分类上要明显好于DBN和BP神经网络。且SVM的K1,K3和 K5的识别率高达99.7%,99.8%和99.6%。对F2,F5和F9的识别率也分别高达96.3%,95.2%和93.8%。这说明SVM的在次型分类上与DBN和BP神经网络相比具有更好的实用性。与表1的对比中可知:DBN和BP神经网络对K,F型恒星的识别率高于对K,F次型的识别率,而SVM对K,F次型的识别率高于对K,F型恒星的识别率。表明DBN和BP神经网络更适合构建K,F型的恒星分类器,利用SVM在次型的分类上能构建更好的恒星分类器。
结合表2与表3可知,SVM可以对不属于K次型的数据进行100%的剔除。这说明了SVM可以对未分类的光谱数据进行筛选和分类。
4 总 结
研究了DBN,SVM以及BP神经网络在光谱分类上的应用。通过比较这三种算法在光谱分类中的应用,可知:在DBN和BP神经网络更适合构建K,F型的恒星分类器,不适合构建K,F次型恒星的分类器,SVM则K,F型的恒星和K,F次型恒星分类上都具有较高的适合率,且在对K,F次型恒星分类上的优势尤为突出,利用其构建K,F次型恒星分类器具有更好的分类效果。
由于SVM可以对不属于K次型的数据进行100%的剔除,介于目前的分类器只能对其训练的类别进行分类,这一方法可以运用到对以后未知的光谱数据的筛选中去,并通过筛选出的数据对未知光谱进行分类。
[1] LI Xiang-ru, HU Zhan-yi, ZHAO Yong-heng(李乡儒,胡占义,赵永恒). Spectroscopy and Spectral Analysis(光谱学与光谱分析),2007,27(9): 1898.
[2] HU Zhen, FU Kun, ZHANG Chang-shui(胡 振,傅 昆,张长水). Journal of Computer Research and Development(计算机研究与发展),2014, 51(9): 1945.
[3] Kuremoto T,Kimura S,Kobayashi K,et al. SI, 2014, 137: 47.
[4] LIU Jian-wei, LIU Yuan, LUO Xiong-lin(刘建伟,刘 媛,罗雄麟). Application Research of Computers(计算机应用),2014,31(7):1921.
[5] XIONG Yu-hong, WEN Zhi-yu, CHEN Gang, et al(熊宇虹,温志渝,陈 刚,等). Acta Photonica Sinica(光子学报),2005,34(10):1514.
[6] RUAN Hua, DAI Lian-kui(阮 华,戴连奎). Chinese Journal of Scientific Instrument(仪器仪表学报),2010,31(11):2440.
[7] Ball N M, Brunner R J, Myer A D, et al. The Astrophysical Journal, 2006, 650(1): 497.
[8] Banerji M, Lahav O, Lintott C J, et al. Monthly Notices of the Royal Astronomical Society, 2010, 406(1): 342.
[9] YAN Tai-sheng, ZHANG Yan-xia, ZHAO Yong-heng, et al(严太生,张彦霞,赵永恒,等). Science in China Press(中国科学),2009,39(12):1793.
(Received Jul. 3, 2015; accepted Nov. 12, 2015)
*Corresponding author
The Comparison of Spectral Classification Based on DBN, BP Neural Network and SVM
LI Jun-feng1, WANG Yue-le1, HU Sheng2, HE Hui-ling2*
1. College of Computer and Information, China Three Gorges University, Yichang 443002, China
2. College of Science, China Three Gorges University, Yichang 443002, China
The stellar classification was an important research field for understanding the formation and evolution of stars and galaxies. With large sky surveys and its massive data, the speed and accuracy of the celestial automatic classification was very important. The depth confidence neural network (DBN), support vector machines (SVM) and BP neural networks used in the star classification were compared in this paper. And the applicability of star classification with these three methods was analyzed. First, K, F stars are classified according to the depth of confidence neural network and BP neural network and support vector machine.Then the K1, K3, K5 sub-type and F2, F5, F9 sub-type were separately identified. Finally, the data which did not belong to the k sub-type were excluded by a secondary classification model based on SVM support vector machine . The results shows that: the depth of belief networks is better for K, F-type star classification, but it is poor for K, F sub-type classification results; The recognition rate of SVM is high for the K, F-type stars and the classification effects of this method is better for K, F-type stars than the corresponding sub-type stars by comparison; The recognition rate of BP neural network is ordinary general for K, F-type stars and their sub-types. The experiment showed that the accuracy of excluding non-k-sub-type data can be up to 100% which indicates that the unknown spectral data can be screened and classified with SVM.
Depth belief networks;BP neural network;Support vector machine;SVM spectra classification
2015-07-03,
2015-11-12
国家自然科学基金天文联合基金项目(U133113),湖北省教育厅科研项目(B2015251),三峡大学科学基金项目(KJ2013B018)资助
李俊峰,1993年生,三峡大学计算机与信息学院本科学生 e-mail: 1097009502@qq.com *通讯联系人 e-mail: hlhe1980@163.com
TN911.7
A
10.3964/j.issn.1000-0593(2016)10-3261-04
- 光谱学与光谱分析的其它文章
- Gd靶激光等离子体光源离带辐射及其等离子体演化的研究
- Probing the Binding of Torasemide to Pepsin and Trypsin by Spectroscopic and Molecular Docking Methods
- Mn(Ⅱ)-5-Br-PADAP共沉淀-火焰原子吸收光谱法测定虾、贝样中的镉
- Near Infrared Spectroscopy Study on Nitrogen in Shortcut Nitrification and Denitrification Using Principal Component Analysis Combined with BP Neural Networks
- 内蒙古草原植被最大光能利用率取值优化研究
- 健康和糖尿病大鼠红细胞荧光光谱非线性程度差异

