固体热载体法褐煤热解过程中的传质传热特性
李方舟,李文英,冯杰
(太原理工大学煤科学与技术教育部和山西省重点实验室,山西省煤科学与技术省部共建国家重点实验室培育基地,山西 太原 030024)
固体热载体法褐煤热解过程中的传质传热特性
李方舟,李文英,冯杰
(太原理工大学煤科学与技术教育部和山西省重点实验室,山西省煤科学与技术省部共建国家重点实验室培育基地,山西 太原 030024)
2015-05-12收到初稿,2015-11-06收到修改稿。
联系人:李文英。第一作者:李方舟(1990—),男,博士研究生。
Foundation item: supported by the National Natural Science Foundation of China (51276120,U1361202),the Higher Specialized Research Fund for the Doctoral Program (20121402110016) and the National High Technology Research and Development Program of China(2011AA05A202).
摘要:为揭示在固定床反应器中固体热载体法快速热解褐煤工艺过程中的热、质传递机理,建立了固体热载体法褐煤热解过程中的传质传热模型。模型包括球型颗粒的一维非稳态导热方程和基于分布活化能模型的动力学模块,分别采用有限容积法与Matlab软件中遗传算法工具箱对二者进行数值计算。通过呼伦贝尔褐煤热重实验数据与温度测定实验数据分别验证了预测的动力学参数及颗粒传热模型结果。研究发现,热、质变化在固体热载体法褐煤热解工艺中呈现复杂的耦合特性。此外,考察了在不同初始温度、热载体进料比与煤颗粒半径条件下,褐煤在热解过程中颗粒内部温度场在径向上随时间的变化规律,并分析了产物释放速率与温度场的关联性,结果表明热历程改变是工艺条件对热解产物分布造成影响的根本原因。
关键词:固体热载体;褐煤热解;传热;传质;数值模拟
引 言
固体热载体法褐煤热解技术是指在热解条件下,将褐煤与具有载热功能的固体载体混合加热,得到焦油、煤气和半焦的技术,属于褐煤热解提质加工工艺。采用固体热载体作为给热介质,增大了传热面积,避免了外热式热解时焦油在反应器边壁分解的问题。此外,褐煤在快速热解条件下,所含的含氧官能团、烷基侧链断裂会形成更多的煤气和焦油,焦油中的脂肪烃、芳烃和酚类物质可加工获得化学品和燃料油,热解半焦热值得到提高,可作为燃烧或气化的合格原料[1],工艺实现了褐煤的分级炼制,提升了氢、氧的元素利用率,是综合利用褐煤资源的有效方式之一。
为了掌握固体热载体煤热解过程中工艺条件对产物组成及分布的作用规律,许多学者从实验分析与模型计算两个角度进行了研究。其中通过建立数学模型来研究固体热载体法煤热解工艺引起了越来越多的关注,例如,Liang等[2]针对移动床固体热载体热解工艺建立了一维稳态数值模型,包含气相-双固相传热理论与多重反应模型,模型能预测气、煤与热载体的轴向温度以及在不同操作条件下产物的变迁,但忽略颗粒内温度梯度;郭治等[3]用差分法解固体热载体法热解传热模型,但边界条件仅考察热辐射,并用一级动力学模型描述煤热解挥发分释放过程;王洪亮等[4]对固体间的传热途径做了详尽的分析,建立了热载体球煤粉热解过程的传热模型,计算采用Comsol软件,但简化了能量方程中源项和动力学部分。
尽管通过数值计算的方法来研究固体热载体法煤热解过程方面已有了一定的成果,但由于系统内热量传递不仅方式多样,且与颗粒内传质过程相互影响,并进一步影响产品分布,使机理趋于复杂化,以上对该工艺的数值模拟均对源项部分或热解动力学进行了较大的简化,弱化模型的准确性。
近年来,通过数值模型对大颗粒煤单独热解过程中颗粒内的传热规律的研究逐渐完善。其中,Zhao等[5]采用传热方程和复杂煤热解模型(FGDVC),研究了在流化床或固定床中燃烧的大颗粒煤的热解过程,模型计算将煤热解的热效应设为零;刘训良等[6-7]在Adesanya等[8]与胡国新等[9]基础上,结合分布活化能模型(DAEM)及能量守恒方程对煤颗粒单独热解的传热传质过程建立数学模型,将反应热与挥发分对流散热纳入源项,提升了模型的准确度。因而有必要结合大颗粒煤热解过程规律,建立更全面的数值模型来进一步探究固体热载体法煤热解过程的热、质传递机理。
在褐煤固体热载体固定床热解工艺中,原料煤的Biot数(Bi)大于临界值0.1[10],研究固体热载体法热解的传热过程不宜选用集总热容法,即大颗粒煤内的温度梯度产生传热阻力,会影响毫米级褐煤颗粒的热解反应与传质速率,最终改变产物组成与分布。因此,探究固体热载体与大颗粒煤混合时的质、热传递规律是揭示该工艺中热解产品所经历温度变化的基础,本文通过分析进料比、温度、粒径和停留时间对传热过程的扰动,选择匹配的工艺条件参数,为反应器设计、运行提供理论依据。
1 实验样品及方法
1.1样品
实验所用原料选取呼伦贝尔褐煤,元素分析和工业分析见表1。将原煤破碎、筛分至0.15~0.18 mm及8 mm左右两种粒径的颗粒样品,均置于110℃的烘箱内干燥8 h,之后,用锉刀打磨大粒径的煤粒,制成类球体形状,将处理后的样品均分别放到密封容器内待用。并选取粒径在1.8~2 mm的石英砂样品(SiO2含量达99.5%以上)备用。

表1 呼伦贝尔褐煤的工业分析与元素分析Table 1 Physical properties analysis of Hulunbuir lignite
1.2实验装置
本文建立的固定床实验装置如图1所示,该系统主要由固定床反应器、温控电炉、测温元件和尾气处理装置组成。固定床反应器材质为石英玻璃,为减小挥发分释放过程中的二次反应,反应器的高径比设计为1:1(ϕ60 mm×60 mm),距反应器下端15 mm处安装有石英烧结作为物料支撑板,高纯氮(99.999%)作为载气,从反应器底端进气口吹进,进料口与出气口位于顶端。热电偶6、7分别测量反应器外壁和器内物料表面温度,选用标号WRNK-162的K型热电偶,规格ϕ0.5×600×L2400,允差值为±2.5℃,灵敏度能满足测量要求。
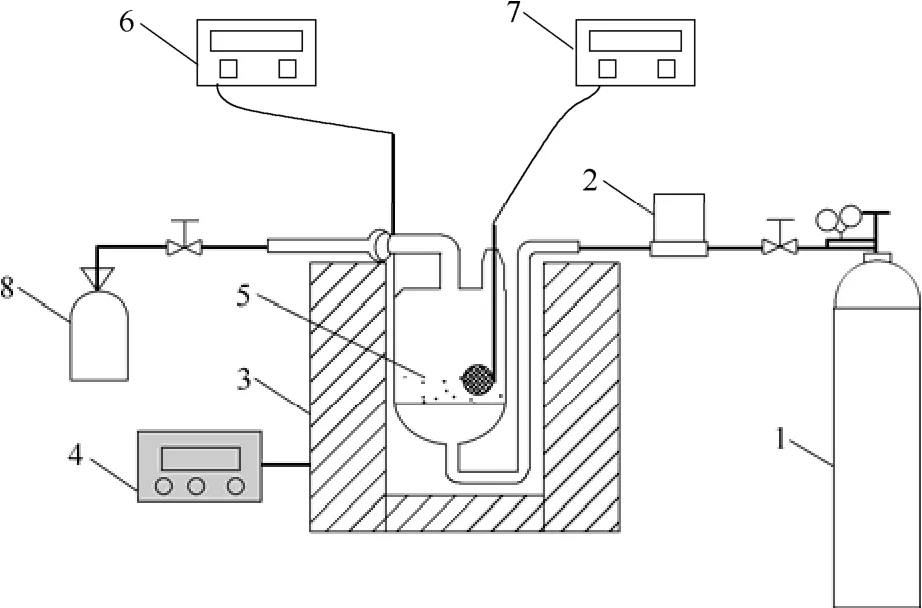
图1 固定床实验装置流程Fig.1 Flowsheet of fixed bed reactor1—N2cylinder; 2—mass flowmeter; 3—heating furnace; 4—temperature controller; 5—quartz reactor; 6,7—thermocouple; 8—off gas collector
1.3实验方法
1.3.1热重实验在HCT-1型热重分析仪(北京恒久科学仪器厂)上,以30 K·min-1升温速率将粒径为0.15~0.18 mm的10.3 mg样品从室温程序升温到1233 K进行热重实验。载气为高纯氮(99.999%),流量为100 ml·min-1。
1.3.2测温实验热电偶分别用铜丝固定在单颗煤粒表层和中心,采集所在部位温度信息。设定加热炉升温程序及载气流量参数,待系统稳定运行后,将石英砂按一定质量比例加入固定床反应器,并将反应器置于加热炉中,在石英砂达到设定温度后,将反应器迅速移出加热炉,同时将连有热电偶的煤颗粒插入反应器,使煤颗粒进入石英砂热载体床层,开始记录时间和温度,在显示温度开始从峰值缓慢下降时,认为进入散热阶段,停止计时。
2 模型建立与数值分析方法
在固定床反应器中用固体热载体使褐煤热解的过程包含复杂的热量传递机理。在固定床反应器中将预热后的固体热载体(石英砂)与煤快速混合,热载体向周围环境发散热量,煤颗粒表面先受到气-固间对流与固-固间辐射的传热作用,部分直接接触热载体的煤会发生导热现象。热流从煤颗粒表层经固相向中心传递,整个煤颗粒处于热的非稳态,表现为颗粒径向上的温度梯度随时间而变化。在颗粒逐渐升温过程中伴随着煤的分解,热解的反应热会扰动颗粒温度梯度,同时,颗粒内反应速率、孔隙率及物性参数如热导率、比热容等也随温度变化而变动。非黏结性煤释放的挥发分与蒸发的水分以气体形式从孔道内向颗粒表面扩散,经二次反应后进入外部载气,并带走部分热量,如图2所示。
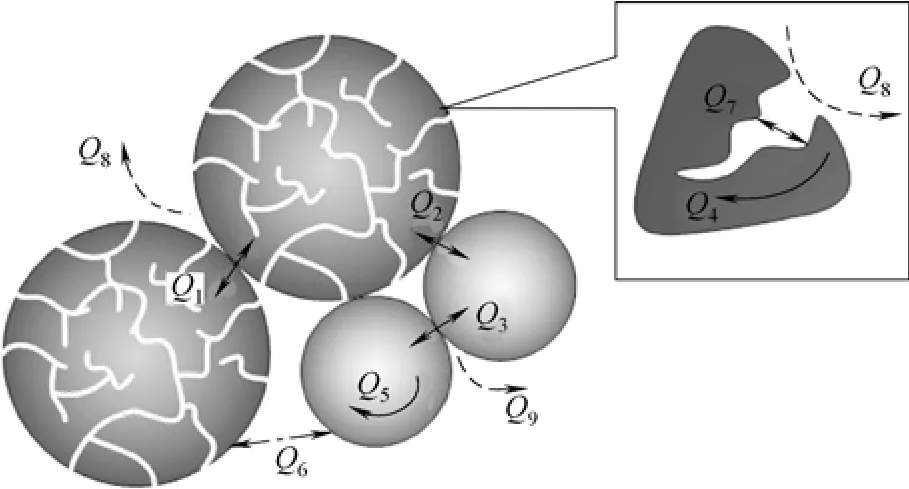
图2 褐煤与固体热载体的传热途径Fig.2 Heat transfer methods between lignite (L) and solid heat carriers (S)Q1—heat transfer interparticles L; Q2—heat transfer between L and S;Q3—heat transfer interparticles S; Q4—heat conduction in L; Q5—heat conduction in S; Q6—heat radiation between L and S; Q7—heat radiation in pores of L; Q8—heat convection between L and volatiles; Q9—heat convection between S and volatiles
针对褐煤固体热载体法热解工艺提出下列假设来简化模型:
(1)假设物料与热载体在极短时间内均匀混合,且忽略固定床内的轴向返混现象,即物料颗粒停留时间相等,受热过程相同;
(2)褐煤与石英砂均认为是实心球形颗粒,在快速热解过程中颗粒形状、体积不变;
(3)假设颗粒内热量传递是一维非稳态过程,传热仅在颗粒径向上发生;
(4)模型未考虑二次反应的影响。
2.1固体颗粒传热模型
褐煤和石英砂的内部由于存在孔隙及孔内的气氛,热量传递是由热传导、对流传热和辐射传热3种基本方式共同完成。在假设颗粒均为实心颗粒后,仅考察最主要的热传导方式,参照固体在球坐标系中的能量守恒方程式分别建立褐煤与石英砂热载体的导热方程。
2.1.1固体热载体颗粒的导热方程固体热载体反应前是等温热源,颗粒表层热量会以接触煤粒传导、相邻煤粒辐射和与气氛对流的方式向外发散,并从热载体内部得到补充。仅作为供热介质无需考虑广义源项,其一维非稳态导热方程[4]
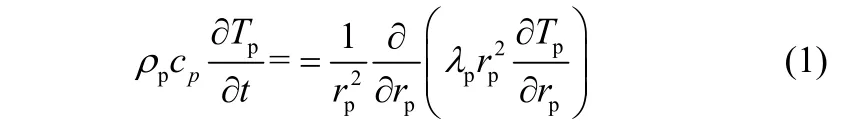
初始条件:边界条件:

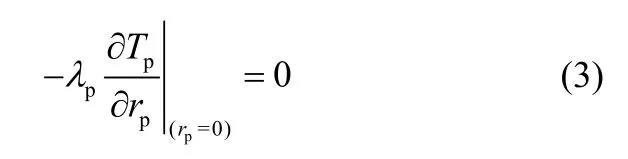
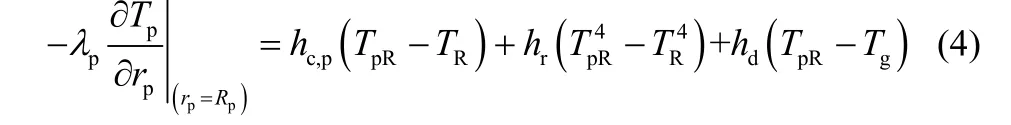
2.1.2煤颗粒的导热方程褐煤受热分解时,热量以颗粒内部气、固相为传递介质,主要的热流向包含外界受热、热解各反应吸放热(含蒸发热)和挥发分逸出的对流热散失。颗粒内部温度梯度的能量平衡方程[6,9]
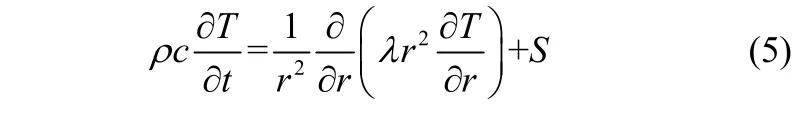
源项S包含了不能归入非稳态相、对流相及扩散相中的一切其他项,式(6)右边3项分别为热解反应热、蒸发热和热解挥发分逸散携带的显热
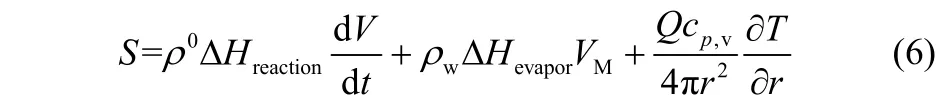
由于认为煤颗粒内部存在热、质传递阻力,挥发分释放速率不再均匀,挥发分在r处质流率为
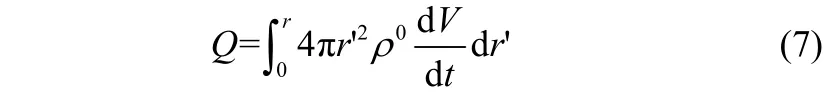
初始条件:

当褐煤快速热解时,挥发分剧烈释放,近似认为环绕颗粒周围气氛与煤粒表面温度相同,忽略对流传热作用。
边界条件:
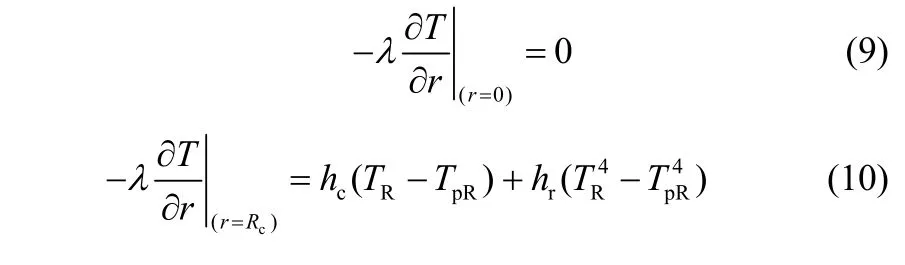
2.1.3质量守恒方程由于已经假设煤颗粒粒径保持不变,可近似得到其质量守恒方程
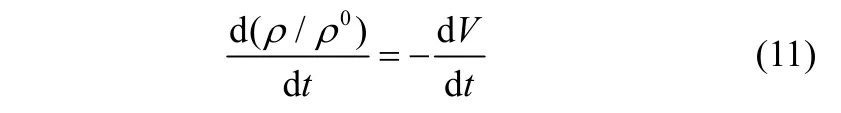
2.2传热模型参数
2.2.1褐煤物性参数的经验公式由于褐煤在受热过程中会发生复杂的热裂解、热缩聚反应,其物性参数在过程中不再是恒定不变的,而是随着热历程与反应程度改变,采用经验公式来表示
比热容[4]

2.2.2传热系数的经验公式
(1)接触传热系数的经验公式
Sun和Chen[11]、Natarajan等[12]以及Watson 等[13]都对颗粒间接触传热问题进行过研究。Watson 等[13-14]曾推导出适用于完全弹性碰撞的光滑理想球体的经验公式,本文传热模型中不考虑煤与固体热载体间的接触应力或摩擦力,可采用这种接触传热系数的经验公式
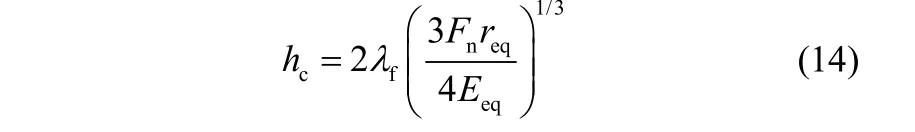
复合热导率
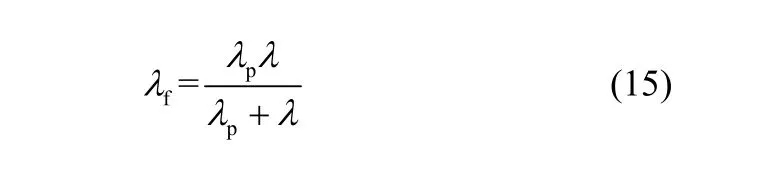
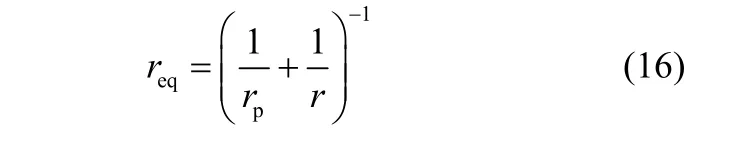
杨氏模量
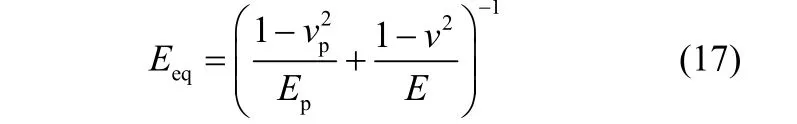
(2)对流传热系数的经验公式
气固相传热系数已有多种经验公式,比如Wakao等[15]和Ranz[16]以及Rowe等[17]气固传热系数模型,可以看出模型中Nu=f(Re,Pr),Re反映了颗粒周围流场惯性力的影响,Pr则体现了气体物理性质的影响,考虑到固体热载体工艺一般包含不同粒径颗粒混合的特点,床层的平均空隙率也应纳入考察,这里采用Gunn[18]提出的经验公式,其偏差较小[5,19]
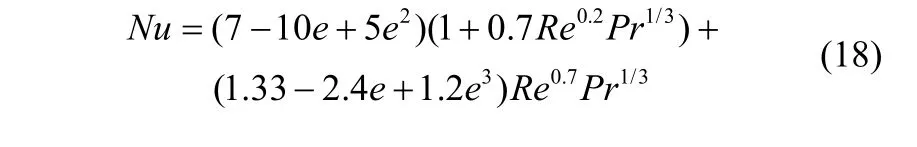
Nusselt数

Prandtl数
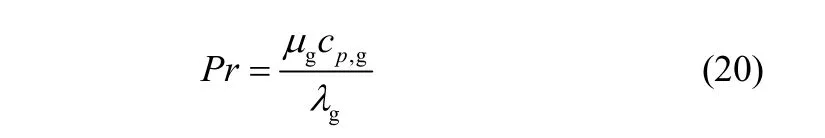
Reynolds数
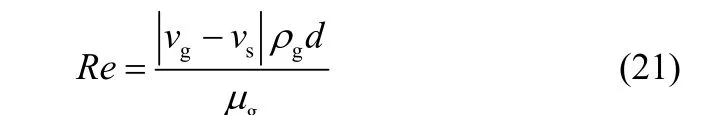
(3)辐射传热系数的经验公式
②文化负载词意义需引申:游览故宫时,导游讲解到:“每一座宫都是一个院落,墙高院深,门户严密。”笔者经过释意分析,认为“院深”意在表现宫殿的封闭和安静,因此并未直接译出其字面含义deep,而是将其解释为closed and quiet.
在工程实际中一般将固体材料视为灰体,引入修正参数系统黑度εδ,则辐射传热系数可表示为

其中,系统黑度[4]为
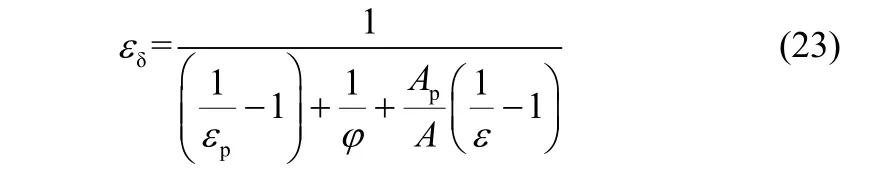
2.3源项中动力学参数模型
源项S公式[式(6)和式(7)]中热解反应速率和对流散热量都由挥发分的释放速率反映。为得到呼伦贝尔褐煤热解挥发分释放的活化能等动力学参数,在模型中引入对煤种和升温速率有宽广适应性的分布活化能模型(DAEM)[20],该模型通过式(24)来计算煤热解到某一时刻挥发分的释放量。
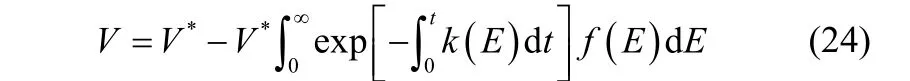
为了方便计算及以热重实验数据验证,将DAEM方程记做非等温条件下热解的DAEM形式
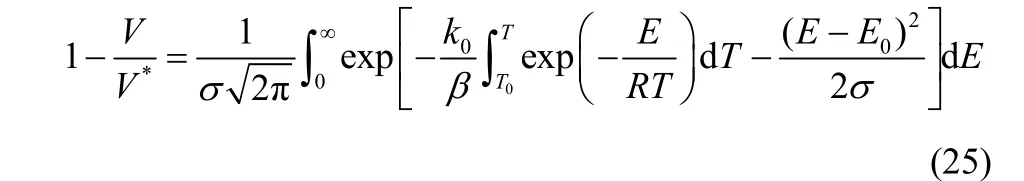
其中,β为褐煤热解的升温速率。
本文所研究的固体颗粒传热模型包含了球形颗粒的一维非稳态导热方程和基于分布活化能模型的动力学模块,其数值求解方法包括以下几个步骤:①采用内节点法将空间区域离散化;②采用有限容积法(FVM)来离散导热方程,离散过程为全隐式格式[21];③采用三对角矩阵法(TDMA)对离散后的方程进行迭代求解;④DAEM公式(25)的内层积分参考文献[22]的方法简化
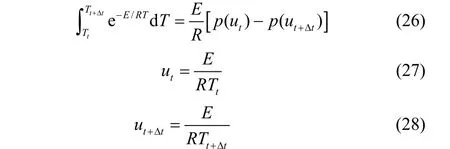
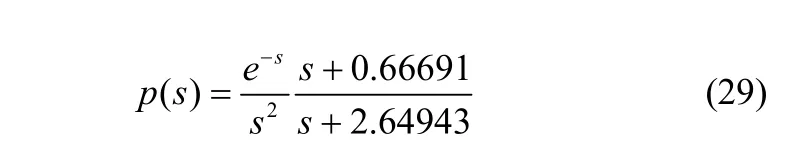
使其适用于离散方程,外层积分用Romberg算法[23]求得高精确度的解;⑤DAEM中的动力学参数采用Matlab软件中的遗传算法工具箱(GAOT)求得。
3 实验结果与讨论
3.1动力学参数求解与验证
为了计算过程的简便,假设热解反应的DAEM中动力学参数均为恒定值。对DAEM公式(25)中的动力学参数E0、k0与σ采用Matlab软件中的遗传算法工具箱(GAOT)来求得最优解[24]。其中在给定的动力学参数范围内(150<E0<300;10<σ<70)[25],目标函数选取各温度下数值解与实验数据的偏差,偏差最小时得E0、k0与σ最优解。
目标函数:
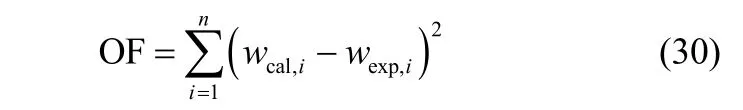
其中,wcal,i、wexp,i分别为不同温度点处失重的数值解和实验值,实验值源自热重数据,实验条件见1.3.1,n为选取的计算点数,程序编制流程见图3。
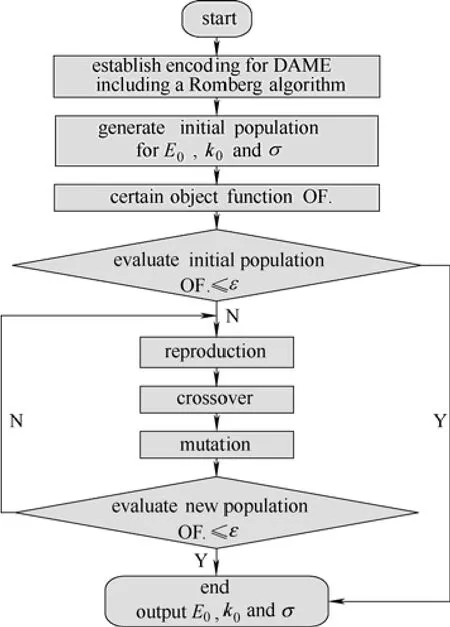
图3 呼伦贝尔褐煤的DAEM动力学参数在GAOT中程序框图Fig.3 Computing programme of GAOT determining kinetic parameters of Hulunbuir lignite in DAEM
结合热重实验数据,将上述程序编制流程在Matlab软件中运行,计算结果为E0=233.14 kJ·mol-1,k0=5.14×1012s-1,σ=29 kJ·mol-1。采用1.3.1实验条件下的热重实验数据对计算结果验证,对比结果见图4。
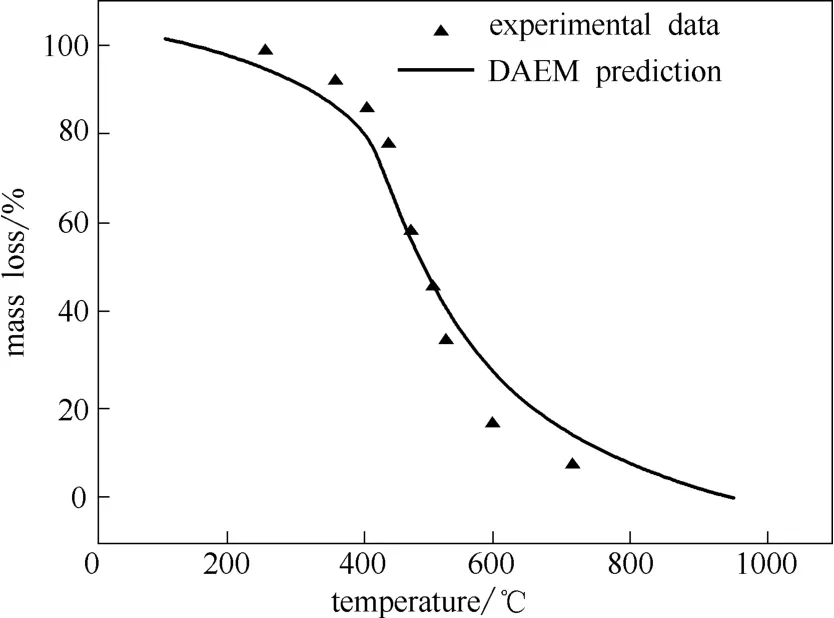
图4 DAEM预测呼伦贝尔褐煤热解相对失重与实验数据的对比Fig.4 Comparison of DAEM prediction and experimental data from lignite thermogravimetric analysis
从预测结果与实验结果的对比发现,用DAEM来预测褐煤热解失重时会与实验值有一定的误差。在DAEM的假设中认为分布活化能E近似为一个正态分布的函数,并将频率因子k0看作定值,在GAOT的编程中接受这一假设。但有研究表明频率因子并非常数,而是会随着活化能的增大而增大,二者之间存在“补偿效应”[20,26]。当采用恒定的频率因子进行计算时会产生误差,且误差会随着温度升高而增大。但由于本文考察褐煤中低温快速热解的热历程,因此忽略上述原因造成的误差影响。
3.2颗粒传热模型的验证
为验证传热模型的正确性,在固定床实验室装置上分别测定了热解过程中煤颗粒表面、中心及石英砂热载体表面的温度,测温实验方法见1.3.2,实验条件设定与表2中工况3的计算参数相同,与传热模型预测结果对比见图5。
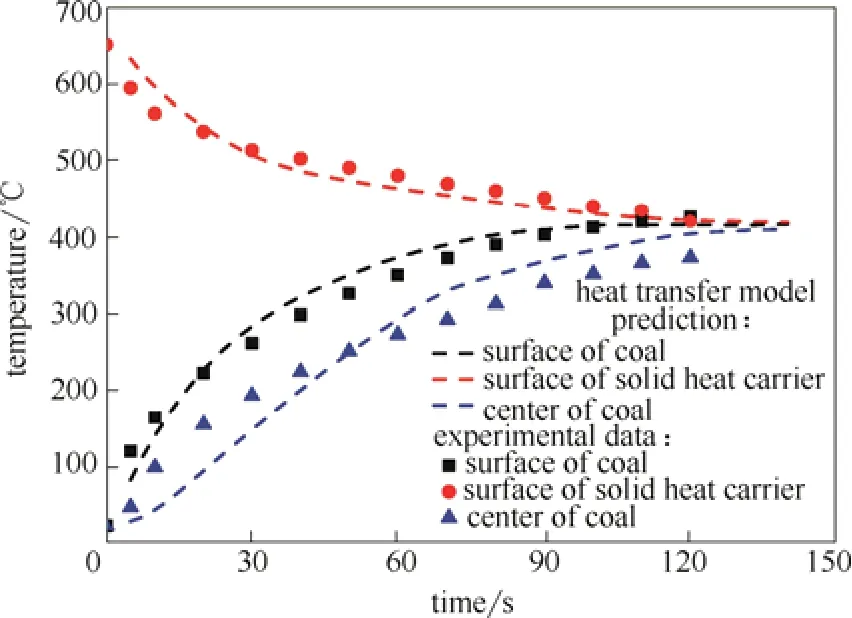
图5 颗粒传热模型预测结果与测温实验数据对比Fig.5 Comparison of particle heat transfer model prediction and temperature measuring experiments
由图5可见,在相同参数条件下,颗粒传热模型的计算结果与实验结果吻合较好,表明建立的模型适用,二者稍有偏差的原因可能是煤颗粒与固体热载体在固定床中接触方式不同,煤颗粒并非均匀受热的理想状态,相互之间的热量传递受到影响。
3.3煤颗粒内部热量传递的计算结果
为了探究不同初始温度、热载体进料比与煤颗粒粒径等工艺条件下,褐煤在热解过程中颗粒内部温度场和产物释放速率随时间在径向上变化规律,表2列举了4种工况下的条件参数。
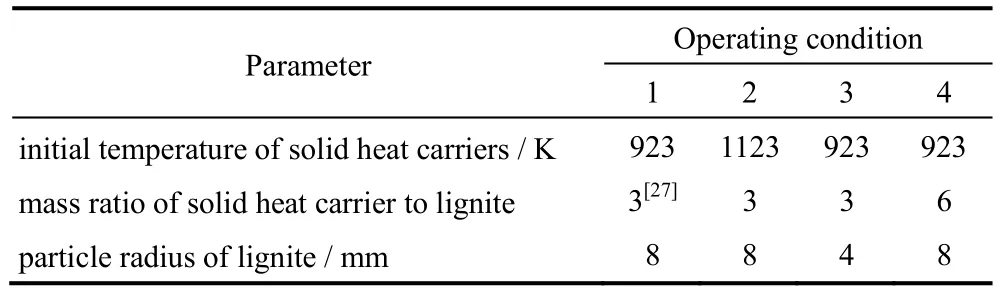
表2 工况参数Table 2 Parameters of operation conditions
图6为对应的4个工况下褐煤颗粒内部温度场随时间在径向上变化的情况。均以工况1[图6(a)]作为基准与其他工况条件进行比较。
工况2是将固体热载体的进料温度提高了200 K,从图6(b)中可见,褐煤颗粒热解最终的平衡温度提升了近220 K,且煤粒达到表面与中心温差低于3 K的时间缩短了约72 s,外层到达650 K仅用了约19 s,可归结为更高初始温度的热载体与煤接触,传热动力正比于温差值,使得颗粒表层升温速率加快,同时也提升颗粒内层热量传递的剧烈程度,煤颗粒内层直到中心在相对较短时间达到均一温度,热解反应快而彻底。煤颗粒表层和中心升温速率相差较大,在到达平衡温度前的某一时刻煤颗粒径向上传热滞后,产生间隔温差很大的温度梯度,在20 s时颗粒外层与中心最大温差约250 K,之后差距会逐渐减小,煤颗粒自身的传热阻力是热解快慢的速控步骤。
工况3是将褐煤粒径缩小一半,从图6(c)中可见在某一时刻,煤颗粒径向上升温速率差距较小,即颗粒内部各层温度梯度不显著,煤粒表面与中心的温差达到小于3 K的时间缩短了约85 s。因为小体积煤颗粒在与固体热载体堆积过程中,会有更多的表面接触到热源,固体间热传导与辐射作用增强;且热量传递到颗粒中心的距离缩短,越靠近颗粒内层其升温速率的提升效果越显著。此外,减小颗粒体积只能促进煤近表面部分的升温均匀程度,但对煤粒内部升温速率以及最终平衡温度影响小。
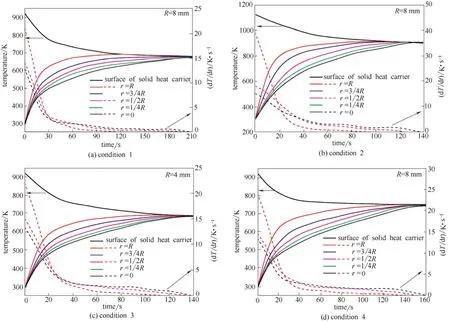
图6 不同工况下褐煤颗粒内部温度场变化情况Fig.6 Changing temperature field in inner particles of lignite under different conditions
工况4是将固体热载体与褐煤的进料质量比增大了一倍,在图6(d)中反映出煤颗粒热解最终平衡温度提升60 K以上,且煤粒表面与中心的温差达到小于3 K的时间缩短了约45 s,煤颗粒表层初始升温速率增大,可以反映出煤颗粒在刚接触热载体时受热均匀,近表面层的热流密度大,这是因为增加固体热载体量加大了有效传热面积;颗粒表层与中心的温度差随时间呈先增大后减小的趋势,但径向上温差减小的幅度不大,颗粒内仍会产生明显的温度梯度。由于煤颗粒表面与颗粒内的传热方式不同,所以颗粒内外呈现出不同的升温曲线,由Fourier定律可知,煤颗粒表面主要受到热传导与热辐射作用,传热系数较大,有效传热面积对热通量影响大,而煤的热导率较小,颗粒内热通量主要受限于传热阻力,固体热载体量增加对煤表层温度场扰动剧烈,但对颗粒内影响较弱;此外,煤热解平衡温度上升是由于系统内初始能量总量增加,更多的热量可供给煤的升温与热解过程。
3.4煤颗粒内部挥发分逸出的计算结果
与温度场类似,颗粒较大的褐煤内部各处的热解反应速率由于受热程度不同步,在颗粒内距表层不同位点处也会出现挥发分瞬时释放量的差异。假设不考虑气体、焦油在逸出过程中的二次反应影响,那么挥发分的释放速率可认为是温度与升温速率的函数,利用温度场的规律就能进一步研究煤颗粒局部挥发分逸出特性。对工况1,褐煤径向上各处挥发分随时间的释放速率如图7所示。
由图7可见,在热解过程中,褐煤颗粒局部挥发分释放速率随时间变化呈抛物线形,沿煤颗粒半径方向的挥发分生成存在“滞后效应”,煤颗粒表面达到最大释放速率的时间比中心提前了约95 s,且越接近颗粒内部挥发分最大释放速率值越高,时间上越滞后,这与文献[6]结果类似。与图6(a)对比,褐煤颗粒内局部挥发分最大释放速率均出现在对应径向上的升温结束阶段,即最终的平衡温度区,可见最大热解反应速率的产生与局部温度和升温速率有内在关联。根据DAEM中活化能分布假设,升温速率会影响煤热解的基元反应途径,造成各反应的活化能呈现某种连续分布的函数形式,使热解反应在不同的温度段具有不同的活化能;DAEM的建立基于Arrhenius方程,反应速率受活化能与温度影响。褐煤在工况1下热解30 s后,颗粒中心升温速率超过表面,且升温阶段比表面长,造成颗粒中心挥发分最大瞬时释放速率大于表面。
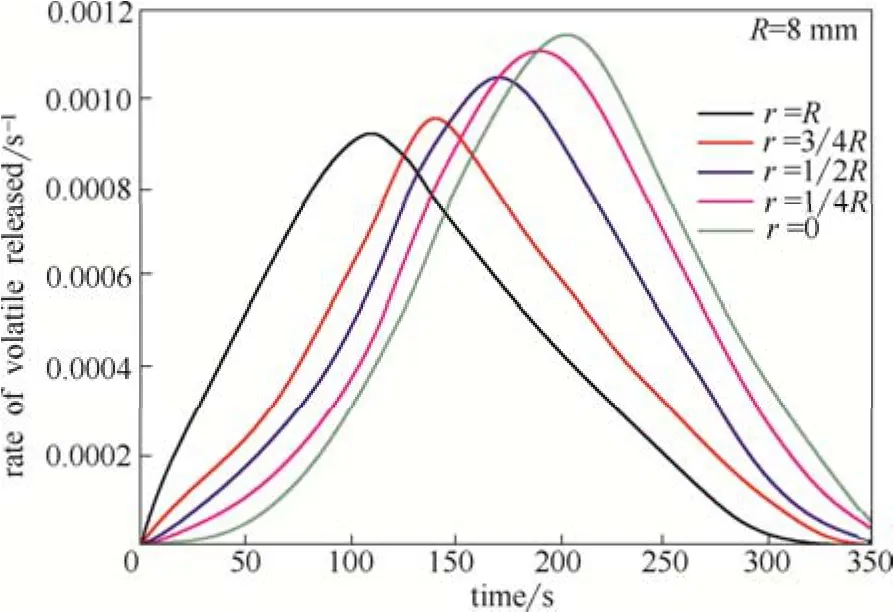
图7 工况1中褐煤颗粒局部挥发分瞬时释放速率Fig.7 Local transient volatile yield rate of a lignite particle under condition 1
在计算过程中,挥发分释放速率是导热方程源项中的一个动力学参数,反映了褐煤热解反应和褐煤与气相对流散热程度,但同时它的计算又依赖于导热方程提供的颗粒内局部的温度数据,体现了质、热传递之间存在复杂的耦合特性。
从计算结果分析,褐煤不断受到固体热载体传递的热量,会发生由表及里推进的热解过程,生成的挥发分以气体的形式从褐煤颗粒的孔道中逸出,释放速率受热解反应和传质的剧烈程度影响。固体热载体向褐煤传热越多,热解反应速率越快,生成大量挥发分,造成颗粒内外的气相浓度差,它与冷热气流的对流作用一起构成了挥发分逸出的驱动力,热量传递主导着这一过程。煤热解挥发分的释放速率规律与煤颗粒热解过程中的热历程之间存在关联性。
4 结 论
用数值模拟结合实验数据分析方法,对固体热载体法热解褐煤这一特定工艺过程中的热、质传递机理进行了研究,详尽考察了煤与固体热载体之间的热量传递方式以及褐煤热解过程中颗粒内部热、质传递间的交互作用;模拟获得了4个不同工况下,煤颗粒径向上温度场的变化规律。此外,还探究了挥发分释放速率在径向上随时间的变化规律,结论如下。
(1)固体热载体法褐煤热解工艺条件的变化均会影响煤颗粒内部的温度场,其中初始温度升高、热载体进料比加大及煤颗粒粒径减小能在不同程度上缩短颗粒整体达到均一、平衡温度的时间,提高热解效率。
(2)煤颗粒内局部的挥发分释放速率随时间表现出类抛物线的变化规律,不同径向上的位点到达速率峰值的时间不同,越接近颗粒中心滞后效应越明显,且在颗粒中心位置挥发分释放速率峰值最高。
(3)在同一工况下,褐煤颗粒内部的温度场与挥发分释放速率之间存在有关联性的变化规律。热历程主导着煤颗粒内部热解反应进度与方式,是工艺条件对热解产物造成影响的根本原因。
对固体热载体法热解褐煤过程,挥发分在大颗粒煤的多孔基质内及固体颗粒间存在对流与扩散的传质现象,并伴随较剧烈的聚合、裂解等二次反应。因此,后续的研究会进一步考察褐煤热解挥发分在颗粒内的传质机理及二次反应作用,探究热、质传递历程中的交互影响,并得出不同工艺条件下的褐煤热解最终产物组成及分布。
符号说明
A——颗粒表面积,m2
c——颗粒比热容,J·kg-1·K-1
cp,g——流体比定压热容,J·kg-1·K-1
cp,v——挥发分比定压热容,J·kg-1·K-1
d——褐煤颗粒粒径,m
E——颗粒杨氏模量,Pa
E0——平均分布活化能,kJ·mol-1
e——床层平均空隙率
Fn——法向应力
ΔHevapor——水分的蒸发热,kJ·kg-1
ΔHreaction——褐煤热解的反应热,kJ·kg-1
R——气体常数,8.314 J·(mol·K)-1
Rc,Rp,r——分别为煤颗粒半径、固体热载体颗粒半径和
颗粒径向上任意位置到中心的距离,m
T,T0,TR——分别为颗粒任意位置温度、颗粒初始温度和
颗粒表面温度,K
Tg——流体温度,K
t——时间,s
V,V*——分别为煤热解挥发分析出量、平衡析出量,ml
VM——工业分析中水分(ad),ml
v——颗粒泊松比
|vg−vs|——气固相相对速率,m·s-1
wC,wH——分别为干燥基下煤中C、H元素的质量分数,%
β ——升温速率,K·s-1
ε ——颗粒黑度
λ,λg——分别为颗粒热导率、流体热导率,W·(m·K)-1
μg——流体动力黏度,kg·(m·s)-1
ρ,ρ0,ρg,ρw——分别为颗粒密度、煤颗粒初始密度、流体密
度和水密度,kg·m-3
σ0——黑体辐射(斯蒂芬‐玻尔兹曼)常数,5.67×
10-8W·m-2·K-4
σ ——活化能分布的标准偏差,kJ·mol-1
φ ——颗粒间角系数
下角标
p ——固体热载体
t,t+Δt ——分别为某时间节点、与时间节点t相差Δt的时间节点
References
[1] 李文英,邓靖,喻长连. 褐煤固体热载体热解提质工艺进展[J]. 煤化工,2012,40(1): 1-5. LI W Y,DENG J,YU C L. Development of lignite pyrolysis with solid heat carrier [J]. Coal Chem. Ind.,2012,40(1): 1-5.
[2] LIANG P,WANG Z F,BI J C. Simulation of coal pyrolysis by solid heat carrier in a moving-bed pyrolyzer [J]. Fuel,2008,87(4/5): 435-442.
[3] 郭治,杜铭华,杜万斗. 固体热载体褐煤热解过程的数学模型与模拟计算[J]. 神华科技,2010,8(2): 69-72. GUO Z,DU M H,DU W D. The mathematical model and simulation of solid heat carrier pyrolysis of lignite [J]. Shenhua Sci. Technol.,2010,8(2): 69-72.
[4] 王洪亮,蒙涛,张华,等. 球型固体热载体煤粉热解过程传热计算及分析[J]. 洁净煤技术,2014,20(3): 90-94. WANG H L,MENG T,ZHANG H,et al. Heat transfer calculation and analysis of coal particle pyrolysis with solid ball heat carrier [J]. Clean Coal Technol.,2014,20(3): 90-94.
[5] ZHAO Y X,SERIO M A,SOLOMON P R. A general model for devolatilization of large coal particles [J]. Symp. (Int.) Combust.,1996,26(2): 3145-3151.
[6] 刘训良,曹欢,王淦,等. 煤颗粒热解的传热传质分析[J]. 计算物理,2014,31(1): 59-66. LIU X L,CAO H,WANG G,et al. Numerical analysis of heat and mass transfer during pyrolysis of coal particle [J]. Chin. J. Comput. Phys.,2014,31(1): 59-66.
[7] LIU X L,WANG G,PAN G,et al. Numerical analysis of heat transfer and volatile evolution of coal particle [J]. Fuel,2013,106: 667-673.
[8] ADESANYA B A,PHAM H N. Mathematical modelling of devolatilization of large coal particles in a convective environment [J]. Fuel,1995,74(6): 896-902.
[9] 胡国新,田学伟,许伟,等. 大颗粒煤在移动床中的热解模型[J].上海交通大学学报,2001,35(5): 733-736. HU G X,TIAN X W,XU W,et al. Devolatilization model of large coal particles in moving bed [J]. J. Shanghai Jiaotong Univer.,2001,35(5): 733-736.
[10] CHERN J S,HAYHURST A N. A simple theoretical analysis of the pyrolysis of an isothermal particle of coal [J]. Combust. Flame,2010,157(5): 925-933.
[11] SUN J,CHEN M M. A theoretical analysis of heat transfer due to particle impact [J]. Int. J. Heat Mass Transfer,1988,31(5): 969-975.
[12] NATARAJAN V V R,HUNT M L. Heat transfer in vertical granular flows [J]. Exp. Heat Transfer,1997,10(2): 89-107.
[13] WATSON L V,MCCARTHY J J. Heat conduction in granular materials [J]. AIChE J.,2001,47(5): 1052-1059.
[14] BHARADWAJ R,KETTERHAGEN W R,HANCOCK B C. Discrete element simulation study of a Freeman powder rheometer [J]. Chem. Eng. Sci.,2010,65(21): 5747-5756.
[15] WAKAO N,KAGUEI S,FUNAZKRI T. Effect of fluid dispersion coefficients on particle-to-fluid heat transfer coefficients in packed beds: correlation of Nusselt numbers [J]. Chem. Eng. Sci.,1979,34(3): 325-336.
[16] RANZ W E. Friction and transfer coefficients for single particles and packed beds [J]. Chem. Eng. Prog.,1952,48(5): 247-253.
[17] ROWE P N,CLAXTON K T,LEWIS J B. Heat and mass transfer from a single sphere in an extensive flowing fluid [J]. Trans. Inst. Chem. Eng.,1965,43(1): T14-T31.
[18] GUNN D J. Transfer of heat or mass to particles in fixed and fluidised beds [J]. Heat Mass Transfer,1978,21(4): 467-476.
[19] 郭雪岩,柴辉生,晁东海. 大颗粒流化床传热数值模拟与气固传热模型比较[J].上海理工大学学报,2012,34(1): 81-87. GUO X Y,CHAI H S,CHAO D H. Numerical simulation of large particle fluidized bed and comparison of gas-particle heat transfer models [J]. J. Univ. Shanghai Sci. Technol.,2012,34(1): 81-87.
[20] 杨景标,张彦文,蔡宁生. 煤热解动力学的单一反应模型和分布活化能模型比较[J]. 热能动力工程,2010,25(3): 301-305. YANG J B,ZHANG Y W,CAI N S. A comparison of a single reaction model with a distributed activation energy one based on coal pyrolysis kinetics [J]. J. Eng. Therm. Energy Power,2010,25(3): 301-305.
[21] 陶文铨. 数值传热学[M]. 上海: 上海交通大学出版社,2001: 79-103. TAO W Q. Numerical Heat Transfer [M]. Shanghai: Shanghai Jiaotong University Press,2001: 79-103.
[22] CAI J M,YAO F S,YI W M,et al. New temperature integral approximation for nonisothermal kinetics [J]. AIChE J.,2006,52(4): 1554-1557
[23] GAO F. Applications of matlab in mathematical analysis [J]. J. Software,2011,6(7): 1225-1229.
[24] 孙玉凤,高虹,王通洲. 生物质热解分布活化能模型的遗传算法实现[J]. 沈阳理工大学学报,2010,29(3): 63-66. SUN Y F,GAO H,WANG T Z. Application of genetic algorithm in distributed activation energy model of biomass pyrolysis [J]. J. Shenyang Ligong Univ.,2010,29(3): 63-66.
[25] MUSTAFA G,SEMMIN F. A direct search method for determination of DAEM kinetic parameters from nonisothermal TGA data (note) [J]. Appl. Math. Comput.,2002,130: 619-628.
[26] MIURA K,MAKI T. A simple method for estimating f(E) and k0(E) in the distributed activation energy mode [J]. Energy Fuels,1998,12: 864-869.
[27] YI Q,FENG J,LU B C,et al. Energy evaluation for lignite pyrolysis by solid heat carrier coupled with gasification [J]. Energy Fuels,2013,27(8): 4523-4533.
Characteristics of mass and heat transfer in lignite pyrolysis with solid heat carrier
LI Fangzhou,LI Wenying,FENG Jie
(Key Laboratory of Coal Science and Technology of Ministry of Education and Shanxi Province,Training Base of State Key Laboratory of Coal Science and Technology Jointly Constructed by Shanxi Province and Ministry of Science and Technology,Taiyuan University of Technology,Taiyuan 030024,Shanxi,China)
Abstract:A comprehensive numerical model coupled two correlative one-dimensional unsteady heat conduction equations of spherical particle with distributed activation energy model has been developed for heat and mass transfer mechanism in lignite pyrolysis with solid heat carrier. The finite volume method and the genetic algorithm optimization toolbox based on Matlab software were employed to calculate the thermal and dynamic parameters,separately,and the reliability of the predictions was further validated by thermogravimetric data of the Hulunbuir lignite and temperature measuring experiment on a laboratory-scale fixed bed reactor,respectively. It was found that the variations in mass and heat transfer during lignite pyrolysis with solid heat carrier showed a complex coupling characteristic. The time-dependent rules of temperature field in radial direction have been obtained by varying operation conditions,such as coal particle radius,the initial temperature and feed amount of solid heat carrier. Besides,the relationship between the releasing rate of pyrolytic products and temperature field revealed that the change of temperature field with heating time in lignite pyrolysis was the primary cause of differentdistribution of the pyrolytic products.
Key words:solid heat carrier; lignite pyrolysis; heat transfer; mass transfer; numerical simulation
基金项目:国家自然科学基金项目(51276120,U1361202);高等学校博士学科点专项科研基金(20121402110016);国家高技术研究发展计划项目(2011AA05A202)。
Received date: 2015-05-12.
Corresponding author:LI Wenying,ying@tyut.edu.cn
DOI:10.11949/j.issn.0438-1157.20150598
中图分类号:TQ 021
文献标志码:A
文章编号:0438—1157(2016)04—1136—09

