分布式拉杆转子扭转振动系统动力学特性分析*

李忠刚陈照波焦映厚梁廷伟侯磊

（1.哈尔滨工业大学机电学院，哈尔滨 150001）（2.哈尔滨工业大学航天学院，哈尔滨 150001）



分布式拉杆转子扭转振动系统动力学特性分析*

李忠刚1，2†陈照波1焦映厚1梁廷伟2侯磊2

（1.哈尔滨工业大学机电学院，哈尔滨 150001）（2.哈尔滨工业大学航天学院，哈尔滨 150001）

摘要为了更好的提高能源利用率，以新兴、高效的分布式拉杆转子系统为代表的燃气轮机与蒸汽轮机联合发电技术在电力部门得到快速发展.本文主要研究了分布式拉杆转子系统扭转振动的非线性动力学特性，通过等效简化等方法建立了分布式拉杆转子系统扭转振动方程.利用平均法获得动力学方程解析解和系统扭转振动幅频曲线，进一步研究了其周期解的稳定特性，并发现系统阻尼，立方刚度和外激频率等参数对其影响规律.本文的分析结果对燃气轮机转子系统动力学设计具有一定的指导意义.

关键词非线性转子动力学， 分布式拉杆转子， 扭转振动， 平均法， 稳定性分析

2015-03-06收到第1稿，2015-10-14收到修改稿.

*国家自然科学基金资助项目（11302058，11272100）和中国博士后面上基金资助项目（2013M541360）

引言

目前，燃气-蒸汽联合循环机组（Gas - Steam Combined Cycle，GSCC）和整体煤气化燃气-蒸汽联合循环机组（Integrated Gasification Combined Cycle，IGCC）发电是当今国际上先进的洁净煤发电技术，具有高效、低污染、节水和综合性能高等优点.此外，由于燃气轮机拥有功率密度大、启动速度快和噪声低频分量低等先天优势，也被广泛应用在航空、舰船和车辆等动力机械中.伴随着燃气轮机技术的发展，分布式拉杆转子在重型和轻型燃气轮机中获得了广泛的应用.分布式拉杆转子是燃气轮机的核心部件，其转子动力学特性决定了机组的整机工作性能.但是研究拉杆转子力学模型及其振动特性的文献起步较晚，且结果不多［1］.目前，国内对拉杆转子系统动力学研究主要集中在对弯曲振动方面的研究，主要包括拉杆转子力学建模［1 -2］，拉杆接触刚度计算［3］、临界转速计算［4 -5］.而关于拉杆转子扭振方面的研究并不多见［6 -7］，本文将根据分布式拉杆转子结构特征进行简化，并建立扭转振动的动力学模型，并利用平均法研究分布式拉杆转子扭转振动非线性系统主共振幅频特性，进一步研究分布式拉杆非线性转子系统主共振周期解的稳定性，为分布式拉杆转子扭转振动特性研究提供一种理论分析方法，并为后续试验研究提供理论指导及基础.

1 分布式拉杆转子扭转振动模型

一般盘式分布拉杆燃汽轮机转子结构可以简化如图1所示.为方便对拉杆转子扭转振动进行研究，不考虑各个拉杆两端螺栓预紧力等因素对拉杆的扭转振动影响，假设整个转子由N个拉杆组成，每个拉杆为圆柱等截面梁，忽略转速对分布拉杆惯性矩的影响，将每个轮盘的转动惯量等效集总到右端为J；在转子左端旋转面建立固定坐标系Oxyz，转速为ω0，如图1所示；拉杆转子受到扭转作用时，拉杆右端（末端）由原始位置A移动到位置B，在右端建立旋转坐标系Ox′y′z，当扭转力作用时拉杆右端截面变形位移示意图如图2所示.

对单个拉杆进行受力分析，可得一个拉杆由弯曲变形所产生的扭转力矩为：

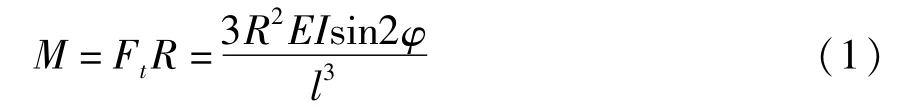
其中，Ft为拉杆弯曲力的切向分量；R为拉杆中心到转子中心的距离；E为弹性模量；I为惯性矩；l为拉杆的长度.

此外，令每个拉杆圆柱面末端扭转角度为2φ，如图2所示，则其圆柱截面的扭转力矩为：

其中，G为剪切弹性模量；Ip为截面的极惯性矩.

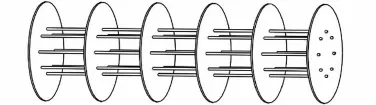
图1 分布式拉杆燃汽轮机转子结构示意简图Fig. 1 Schematic of a distributed rod fastening rotor in the gas turbine

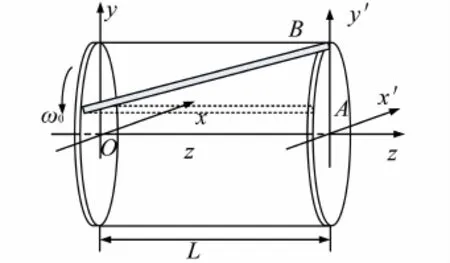
图2 分布式拉杆转子等效简化结构图Fig. 2 Equivalent simplified structure of the distributed rod fastening rotor

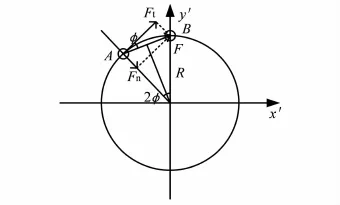
图3 拉杆末端截面位置示意图Fig. 3 Position schematic of the end section of a fastened rod

在实际工程中，燃气轮机分布式拉杆在预紧力作用下，螺母与轮盘之间存在一定的摩擦系数，且各轮盘接触面上也存在摩擦系数；此外，拉杆材料本身拥有抗扭内阻.因此，需要在实际的动力学系统中存在一定的弱阻尼影响，不妨假设其为弱阻尼项系数为εμ；当分布式拉杆转子在扭转外激励Λcosωt作用下，则再可根据上述公式将分布式拉杆转子系统动力学方程写为：

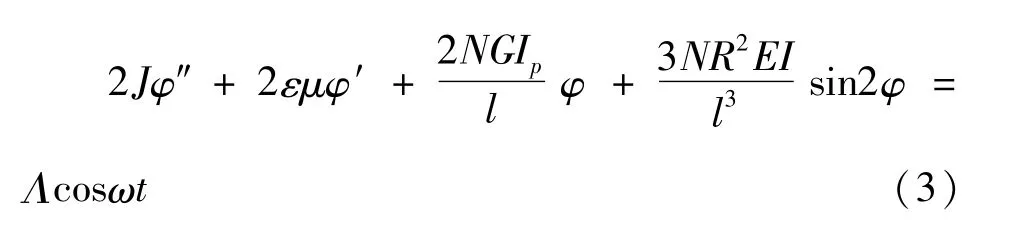
其中，当扭转角度较小时，可由Taylor展开级数得到可知，.因此，动力学系统（3）可简化整理为：

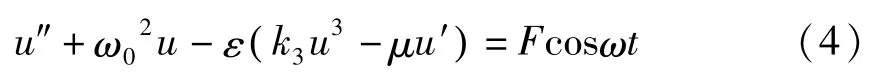
2 非线性扭转振动系统主共振分析

当外激励频率ω接近派生系统频率ω0时，系统发生主共振，由于系统是线性小阻尼系统，这时很小的外激励幅值F就会激发出强烈的共振，此时对外激励幅值和频率加以限制标上小量：F =εF，ω2=ω0

2（1 +εσ），其中σ作为激励频率调谐参数.则动力学系统（4）可表示为：

本文应用平均法［8］可得到动力学系统（5）平均方程为：

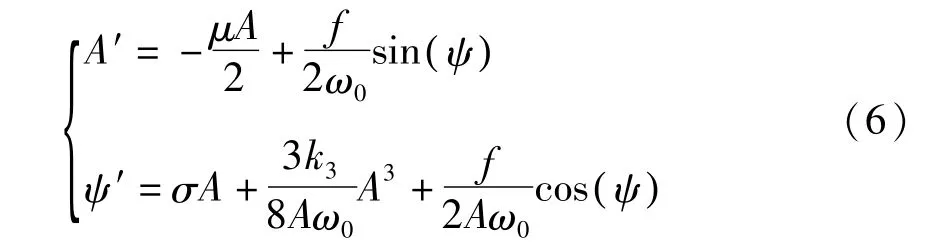
为确定稳态运动定常解振动幅值和相位，则消除三角函数后的系统分岔方程为：

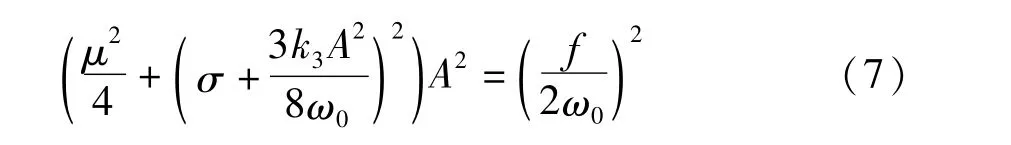
图4为动力学系统（5）不同参数下的幅频曲线，分析可知扭转振动系统的刚度在主共振时有时会表现为软弹簧特性，并幅值存在三解特征，如图中间红曲线是不稳定解，黑曲线为稳定解.图4（a）说明，当系统阻尼系数越高，系统在主共振附近的振动越低，而且当系统阻尼增加到一定程度后，动力学系统将不再会出现跳跃现象，而且振动幅值也会减低，这一现象主要是由于非保守动力学系统中的阻尼将消耗系统振动能量.而外激励的振动幅值与之相反，如图4（b）所示.图4（c）说明系统主共振时的幅频曲线出现软弹簧特性是由于系统非线性刚度引起的，只有当非线性刚度较小时动力学系统会表现出线性振动特性.因此，在实际工程设计时，首先需要在设计参数上避免出现分岔现象，其次需要将振动幅值尽量降低，以便在通过共振区时系统拥有较强的动力学稳定性.

图4 幅频曲线Fig. 4 Frequency response diagrams

3 动力学系统主共振周期解稳定性分析

下面进一步深入研究动力学系统（5）主共振定常解的稳定性边界，进而为转子设计提供理论指导.可将平均方程（6）在周期运动附近线性化，其小扰动Δa和Δψ的自治微分方程可表示为：

由特征方程可得方程（5）定常解解失稳条件为：

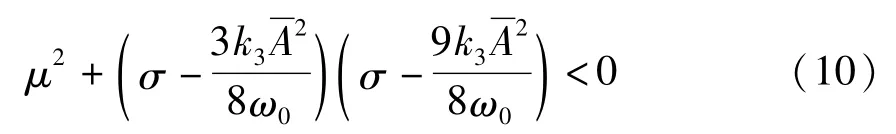
由公式（10）可知，动力学系统（5）的系统参数对其定常解稳定性都会产生影响.如图5所示，为在不同σ值下非线性振动系统幅值A的失稳边界，即转子转速在派生系统固有频率ω0附近变化时，系统不同的振动幅值会导致系统周期解的稳定性发生根本性的改变.可见对于非线性系统，幅值的大小会影响系统周期解的性态.图6为取不同幅值参数下稳定周期解的相图，系统振幅在临界值变化时，系统周期解会有明显变化.

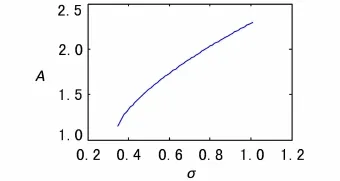
图5 幅值失稳边界Fig. 5 Instability boundary ofamplitude

图6 不同初值下的周期解相图Fig. 6 Phase diagrams for periodic solutions withdifferent initial values

4 总结

对拉杆转子扭转振动非线性动力学模型周期解进行了稳定性分析，研究结果表明：非线性动力学系统中的阻尼、非线性刚度和外激励频率等参数对系统周期解的稳定性有一定的影响，利用Duffing方程扰动方程的稳定性给出了系统周期解失稳判定曲线.此外，振动幅值大小也会影响周期解大小.

因此实际工程中，拉杆转子在设计阶段需要尽量避开公式（13）所给出的导致系统周期失稳的敏感区域；而且当系统产生周期解时，拉杆转子系统在运行中尽量降低突加扭转负荷，即扭转振动幅值，使系统尽量稳定到幅值较小的周期解上.

在文本理论分析基础上，课题组将继续开展扭转振动实验，验证理论分析结果，并通过参数控制实现系统较高的动力学稳定性.

参 考 文 献

1 汪光明，饶柱石，夏松波.拉杆转子力学模型的研究.航空学报，1993，14（8）：419～423（Wang G M，Rao Z S，Xia S B. The analysis of mechanical model of rod fastening rotor. Acta Aeronautica et Astronautica Sinica，1993，14 （8）：419～423（in Chinese））

2 章圣聪，王艾伦.盘式拉杆转子振动特性研究.振动与冲击，2009，28（4）：117～120（Zhang S C，Wang A L. Analysis of vibration characteristics of a disk-rod-fastening rotor. Journal of ViIbration and Shock，2009，28（4）：117 ～120（in Chinese））

3 李辉光，刘恒，虞烈.考虑接触刚度的燃气轮机拉杆转子动力特性研究.振动与冲击，2012（7）：4～8（Li H G，Liu H，Yu L. Dynamic characteristics of a rod fastening rotor for gas turbine considering contact stiffness. Journal of Vibration and Shock，2012，31（7）：4～8（in Chinese））

4 王少波，孟成，苏明.燃气轮机拉杆转子动力学建模及临界转速计算.上海交通大学学报（自然版），2013，V47（3）：381～384（Wang S B，Meng C，Su M. Dynamic modeling and critical speed calculation of gas turbine rod fastening rotor. Journal of Shanghai Jiaotong University （Sci.），2013，47（3）：381～384

5 何鹏，刘占生，张广辉等.分布拉杆转子动力学建模与分析.汽轮机技术，2010，52（1）：4～8（He P，Liu Z S，Zhang G H，et al. Dynamic modeling and analysis of distributed rod fastening rotor. Turbine Technology，2010，52 （1）：4～8（in Chinese））

6 王艾伦，骆舟.拉杆转子扭转振动研究.振动与冲击，2009，28（5）：165～168（Wang A L，Luo Z. Study on rod fastening rotor＇s torsional vibration. Journal of Vibration and Shock，2009，28（5）：165～168（in Chinese））

7 高进，袁奇，李浦等.燃气轮机拉杆转子考虑接触效应的扭转振动模态分析.振动与冲击，2012，31（12）：9～18（Gao J，Yuan Q，Li P，et al. Torsional vibration modal analysis for rod-fastened gas turbine rotor considering contact effects. Journal of Vibration and Shock，2012，31 （12）：9～18（in Chinese））

8 陈予恕.非线性振动.北京：高等教育出版社，2002 （Chen Y S. Nonlinear Vibration. Beijing：Higher Education Press，2002（in Chinese））

Received 6 March 2015，revised 16 October 2015.

*The project supported by National Natural Science Foundation of China（11302058，11272100），Supported by China Postdoctoral Science Foundation（2013M541360）

ANALYSIS OF CHARACTERISTICS OF THE TORSIONAL VIBRATION OF THE DISTRIBUTED ROD FASTENING ROTOR SYSTEM*

Li Zhonggang1，2†Chen Zhaobo1Jiao Yiinghou1Liang Tingwei2Hou Lei2
（1. School ofMechatronics Engineering，Harbin Institute Technology，Harbin 150001，China）（2. School of Astronautics，Harbin Institute Technology，Harbin 150001，China）

AbstractIn order to improve efficiency，the gas and steam turbine cycle technology，represented by newly distributed rod fastening rotor system，gets fast development in electrical production departments. In this paper，

nonlinear characteristics of the distributed rod fastening system are studied by a novel torsional vibration model. By using equivalent and simplification method，torsional vibration model of the distributed rod fastening rotor system are established. Based on the average method，analytical solutions and the amplitude frequency curves of the dynamic system are obtained. Further，the stability of periodic solutions of the dynamic system is studied，and impacts of the external excitation，damping and cubic stiffness are investigated respectively. Analysis results of the dynamic system have a guiding significance to design.

Key wordsnonlinear rotor-dynamics， distributed rod fastening rotor， torsional vibration， average method，stability analysis

DOI：10. 6052/1672-6553-2015-011

通讯作者†E-mail：lizhonggang@ hit. edu. cn

Corresponding author†E-mail：lizhonggang@ hit. edu. cn