薄壁圆柱壳的高阶模态振动特性研究*

王宇罗忠李昌刘 健

（1.辽宁科技大学机械工程学院，鞍山 114051）（2.东北大学机械工程学院，沈阳 110819）



薄壁圆柱壳的高阶模态振动特性研究*

王宇1†罗忠2李昌1刘 健1

（1.辽宁科技大学机械工程学院，鞍山 114051）（2.东北大学机械工程学院，沈阳 110819）

摘要采用解析法研究了不同边界条件下薄壁圆柱壳的高阶模态振动特性.首先基于Love壳体理论，在简支-简支、固支-固支和固支-自由三种边界条件下，通过伽辽金法建立了动力学模型，对模态特性进行求解，得到了高阶固有频率和三维模态振型，并通过文献和有限元法进行了比较.算例结果表明，两端简支边界条件下采用解析法得到的固有频率误差值不超过2%，当周向波数较小时固有频率先减小后增加，在高阶时的固有频率逐渐升高，当轴向半波数增加时固有频率明显增大，通过解析法、文献和有限元法得到的三维模态振型相吻合.

关键词薄壁圆柱壳， 边界条件， 高阶固有频率， 三维模态振型

2014-12-04收到第1稿，2014-12-27收到修改稿.

*国家自然科学基金资助项目（51105187）、辽宁科技大学青年基金资助项目（2014QN13）

引言

薄壁圆柱壳是指壁厚与其它最小特征尺寸之比在1/80和1/5之间的壳体［1］.薄壁圆柱壳构件在航空航天和造船等领域中应用广泛，例如航空发动机的机匣、鼓筒和卫星外壳等，在外界复杂工况下的振动行为复杂，可能会产生高阶共振、失稳和损伤等故障，对薄壁圆柱壳构件的高阶振动特性进行深入研究，具有重要的应用价值.

目前，关于薄壁圆柱壳构件低阶固有特性的研究较多，而许多薄壁壳体的振动疲劳问题中，主要是高阶模态所对应的共振引起的，国外学者的研究成果如下：Rongong J A和Tomlinson G R［2］针对带阻尼层的薄壁圆环，对其高节径（即周向波数）的振动特性进行了研究. Wang C和Lai J C S［3］采用波动方法预测了有限长圆柱壳的固有频率，但没有考虑相应的模态振型. El-Kaabazi N和Kennedy D［4］基于Donnell、Timoshenko和Flügge理论，采用Wittrick-Williams方法研究了变厚度圆柱壳的固有特性，而对高阶模态特性并不太清楚. El-Mously M［5］通过对三种壳体理论方程，仅对固有频率进行了求解.我国学者对圆柱壳类结构的低阶固有特性进行了许多研究，但是对高阶固有频率和三维模态振型的研究较少［6～9］.陈正翔和陈维衡［10］对圆柱壳中较高阶周向模态振动波的频散特性进行了研究，得到了自由振动波随频率变化的规律.韩清凯、王宇和李学军［11］对圆柱壳的高阶固有频率进行了求解，但是没有考虑模态振型的特性［11］.李晖［12］等利用实验方法对约束态圆柱壳的模态振型进行了测试，得到了部分低阶模态振型.陈丽华［13］等用哈密顿原理和Rayleigh - Ritz方法研究了简支、自由和固定边界条件下三阶剪切变形板的固有频率和振型.

针对薄壁圆柱壳构件，基于Love薄壳理论，在简支-简支、固支-固支和固支-自由三种边界条件下，采用解析法对高阶模态特性进行了求解，通过算例分析得到了其高阶固有频率和三维模态振型，并通过相关文献和有限元法对振动特性进行了比较.

1 薄壁圆柱壳的模态特性求解

1. 1 力学模型

如图1所示为薄壁圆柱壳模型.

在柱坐标系Oxθz中，坐标原点O为端面圆心，纵向x轴与轴线重合，径向z轴在端面径向上，切向θ为端面上偏离z轴初始位置的偏转角，u、v和w表示中面上任意一点在轴向、切向和径向的位移，L、H和R分别表示薄壁圆柱壳的长度、厚度与中面半径.

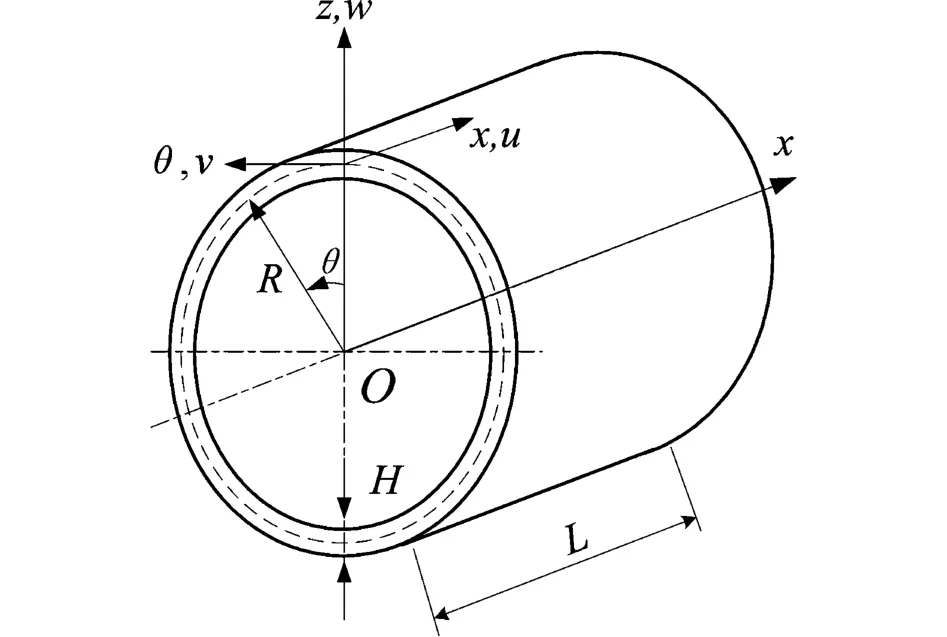
图1 圆柱坐标系中的薄壁圆柱壳模型Fig. 1 thin cylindrical shell in cylindrical coordinate system

1. 2 模态特性求解

薄壳理论假定应力与应变服从Hooke′s定律，各点的振动位移比厚度H小得多，基于Love壳体理论［14］采用位移u（x，θ，t）、v（x，θ，t）和w（x，θ，t）表示的动力学平衡方程为

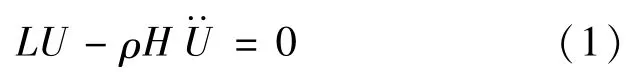
式中，‘·’表示位移对时间的求导，ρ为材料密度，L算子的表达式为

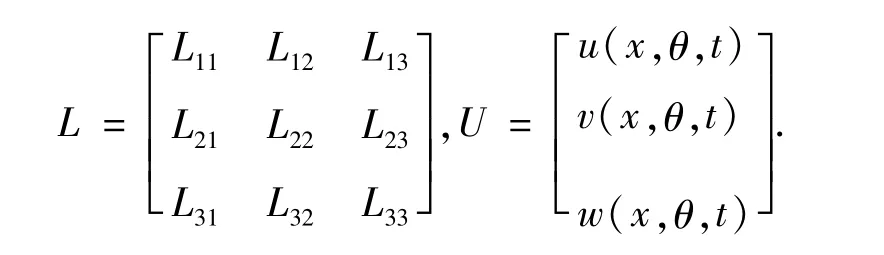
式中，Lij（i，j =1，2，3）表示微分算子，具体表达式为

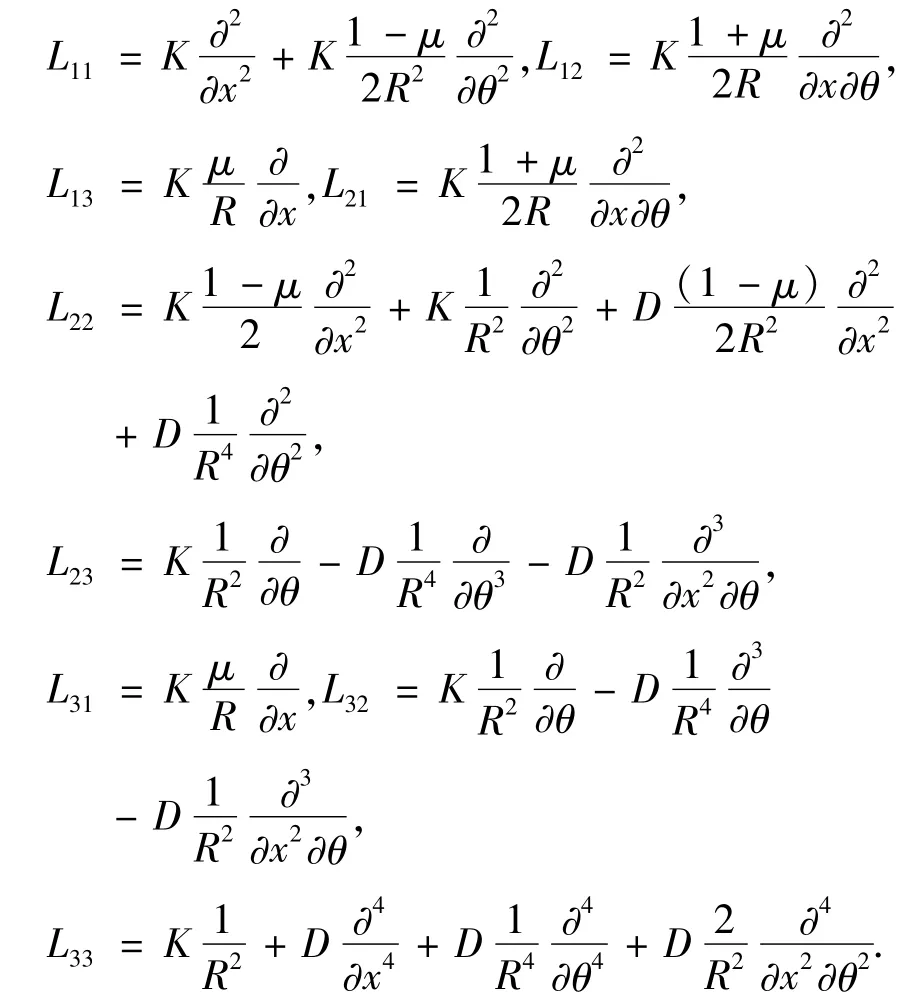
选取振动位移解的形式为

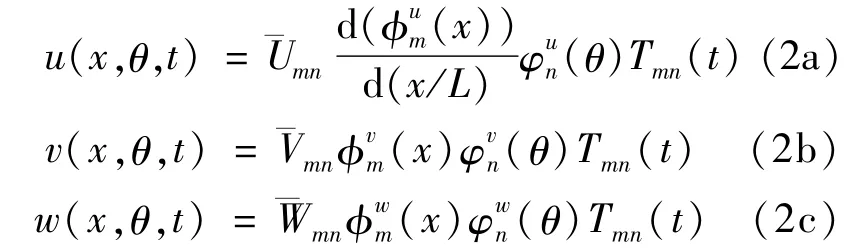
式中，m表示轴向半波数，n表示周向波数，¯Umn、¯Vmn和¯Wmn为振型幅值系数，Tmn（t）为模态坐标，轴向振型函数φkm（x）（k = u，v，w）表示为

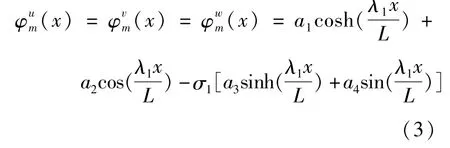
式中，λ1、σ1和αi（i =1，2，3，4）的数值由边界条件确定，具体表达式如下：

（1）简支-简支边界条件

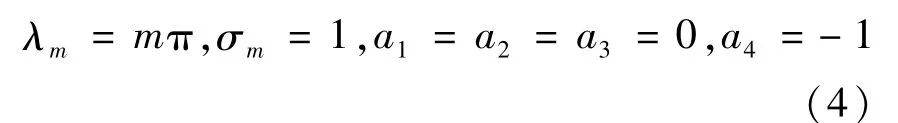
（2）固支-固支边界条件

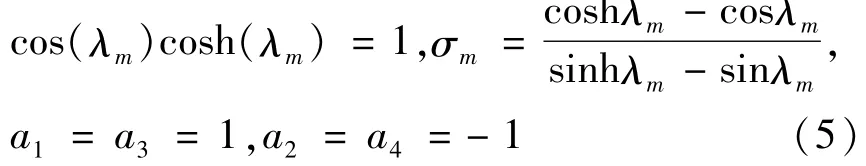
（3）固支-自由边界条件

周向振型函数φkn（θ）（k = u，v，w）表示为

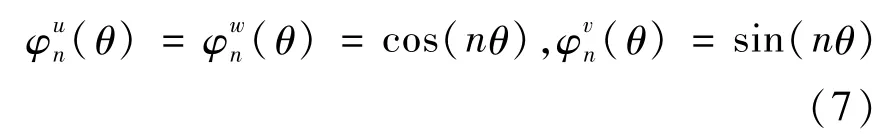
将式（2）代入式（1），进行Galerkin离散得

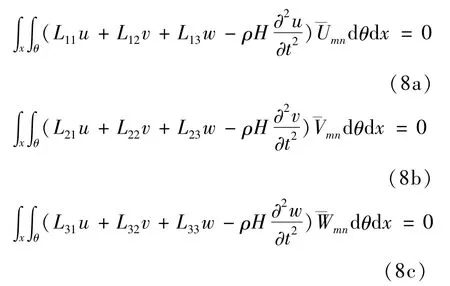
对式（8）进行积分运算，得到固有频率特征方程为

式中，cij（i，j =1，2，3）的具体表达式为

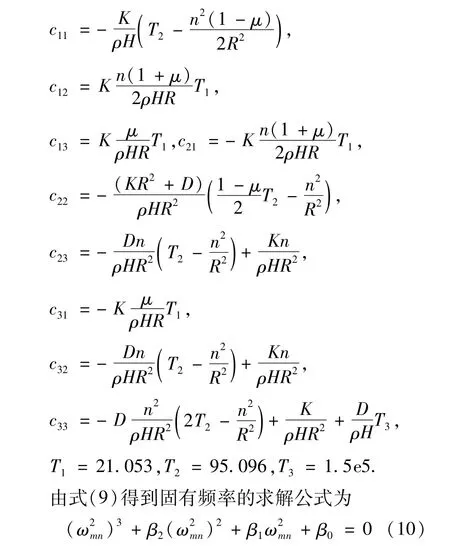
式中，

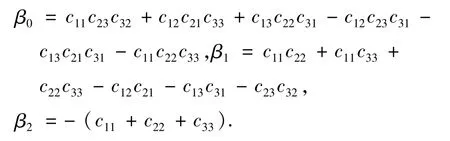
通过式（10）求解固有频率，然后利用振型函数式（2）可得到三种边界条件下对应的三维模态振型.

2 算例分析

利用解析法、有限元法和文献［15］，在简支-简支、固定-固定和固定-自由三种边界条件下，求解薄壁圆柱壳的m = 1～3和n = 1～25阶固有频率和三维模态振型，其材料参数和几何参数如表1所示.利用有限元程序ANSYS进行求解时，取三维高阶实体单元SOLID186，采用VROATA命令从截面绕轴旋转生成圆柱壳模型，通过从相邻面扫掠体的方法生成网格，共计3420个单元，19530个节点.

表1 薄壁圆柱壳的材料参数和尺寸参数Table 1 Material properties and geometric parameters of a thin cylindrical shell

（1）简支-简支边界条件

在简支-简支边界条件下，采用解析法、文献和有限元法得到的各阶固有频率随轴向半波数和周向波数变化的关系如图2所示.由图2（a）可知，通过三种方法求得的固有频率随着周向波数的变化趋势相同，当周向波数较小时，固有频率先减小后增大，当m = 1，n = 7时的固有频率达到最小值2404Hz，当周向波数继续增大时的固有频率逐渐升高；同时，随着轴向半波数的增加固有频率也随之增加，在高阶m =3，n =25时的固有频率达到最大值.由图2（b）可知，通过解析法与文献和有限元法的固有频率误差比较可知，在m =1～3，n = 1～25范围内，固有频率的最大误差值均小于2%，通过文献求得的固有频率值稍大于解析法求得的结果，而通过有限元法求得的固有频率值略小于解析法的频率值，这是因为有限元法是一种近似方法，其模态分析只能针对线性结构，文献得到的结果是基于经验公式，而解析法的位移解是基于梁函数的假设，导致了三种方法计算误差的存在.

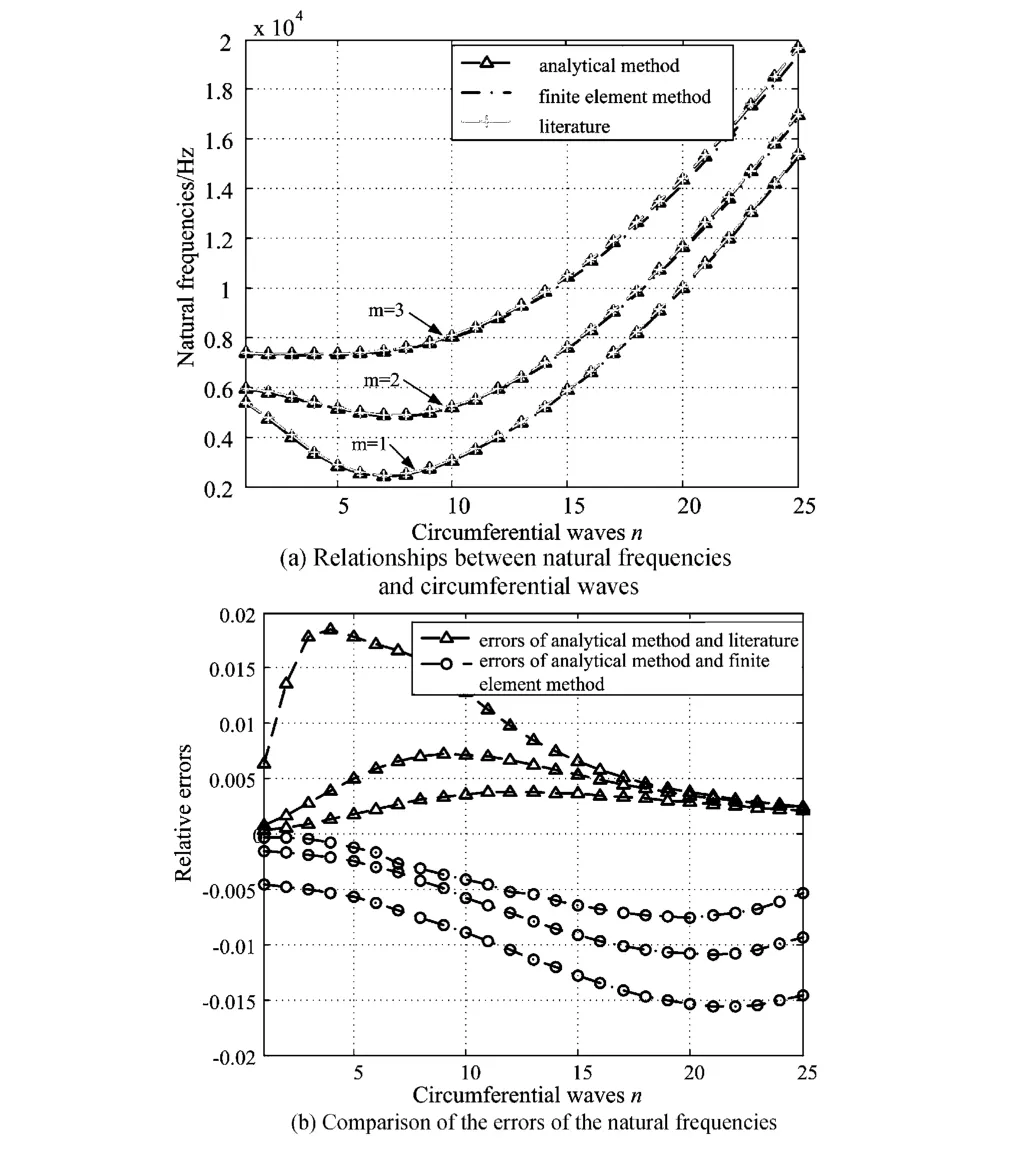
图2 简支-简支边界条件下薄壁圆柱壳的固有频率Fig. 2 Natural frequencies of thin cylindrical shell under simply supported-simply supported boundary condition

薄壁圆柱壳的三维模态振型如表2所示，由解析法和有限元法得到的三维模态振型相互吻合，在圆周方向上表现为均匀的花瓣形状，例如在固有频率最低的第（1，7）阶三维模态振型表现为周向波数为7的花瓣形状；由于两端简支的边界条件对上下两侧边界上节点的限制作用相同，引起壳体中部的振动幅度最大；最低阶模态也是构件最容易发生共振的一阶模态，并且在低阶固有频率的振动模态以周向振动为主.

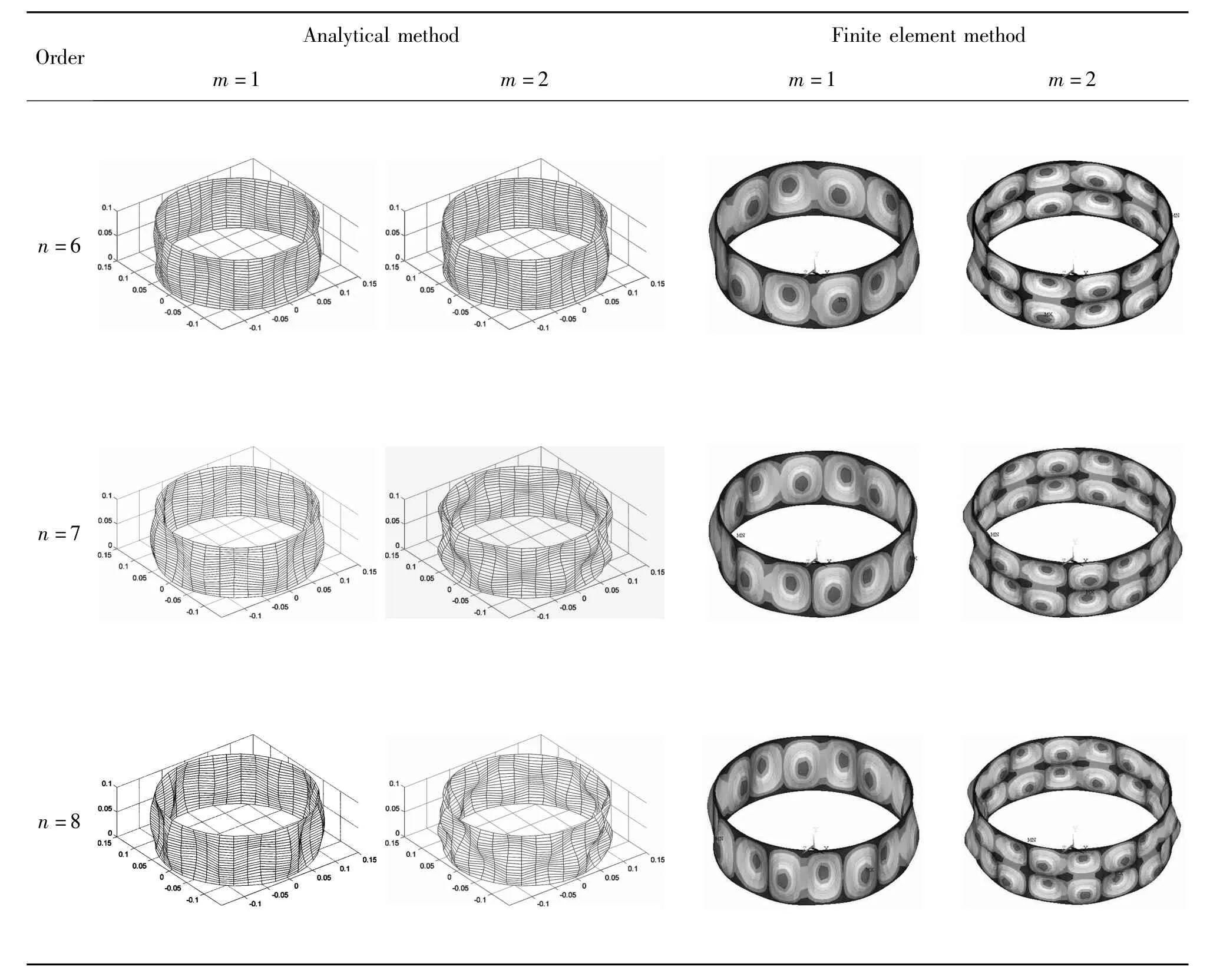
表2 简支-简支边界条件下薄壁圆柱壳的三维模态振型Table 2 3-D modal shapes of a thin cylindrical shell under simply supported-simply supported boundary condition

（2）固支-固支边界条件

在固支-固支边界条件下，薄壁圆柱壳的固有频率变化曲线如图3所示，三维模态振型如表3所示.可以看出，低阶固有频率先减小后增加，当m =1，n =7时的固有频率最小值为3146Hz，高阶固有频率值随着周向波数的增加而逐渐升高；另外，随着轴向半波数的增大，固有频率值也随之增大；薄壁圆柱壳构件的三维模态振型在低阶时以周向模态振动为主，在高阶时出现轴向模态和周向模态的组合振型.这是因为两端固支的边界条件对壳体的作用，限制了边界上各节点的全部自由度，引起中部出现最大振动位移.

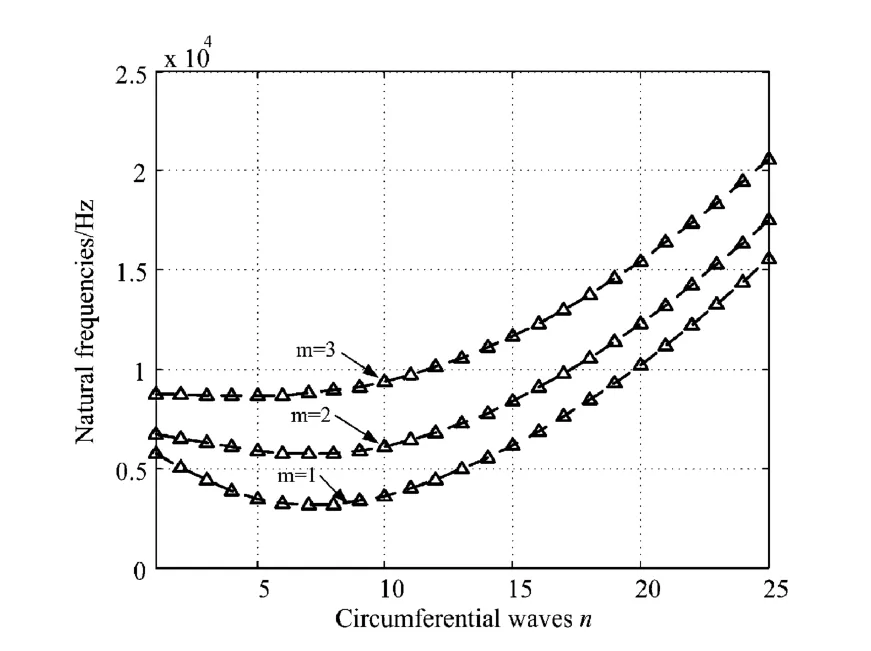
图3 固支-固支边界条件下薄壁圆柱壳的固有频率Fig. 3 Natural frequencies of a thin cylindrical shell under clamped-clamped boundary condition

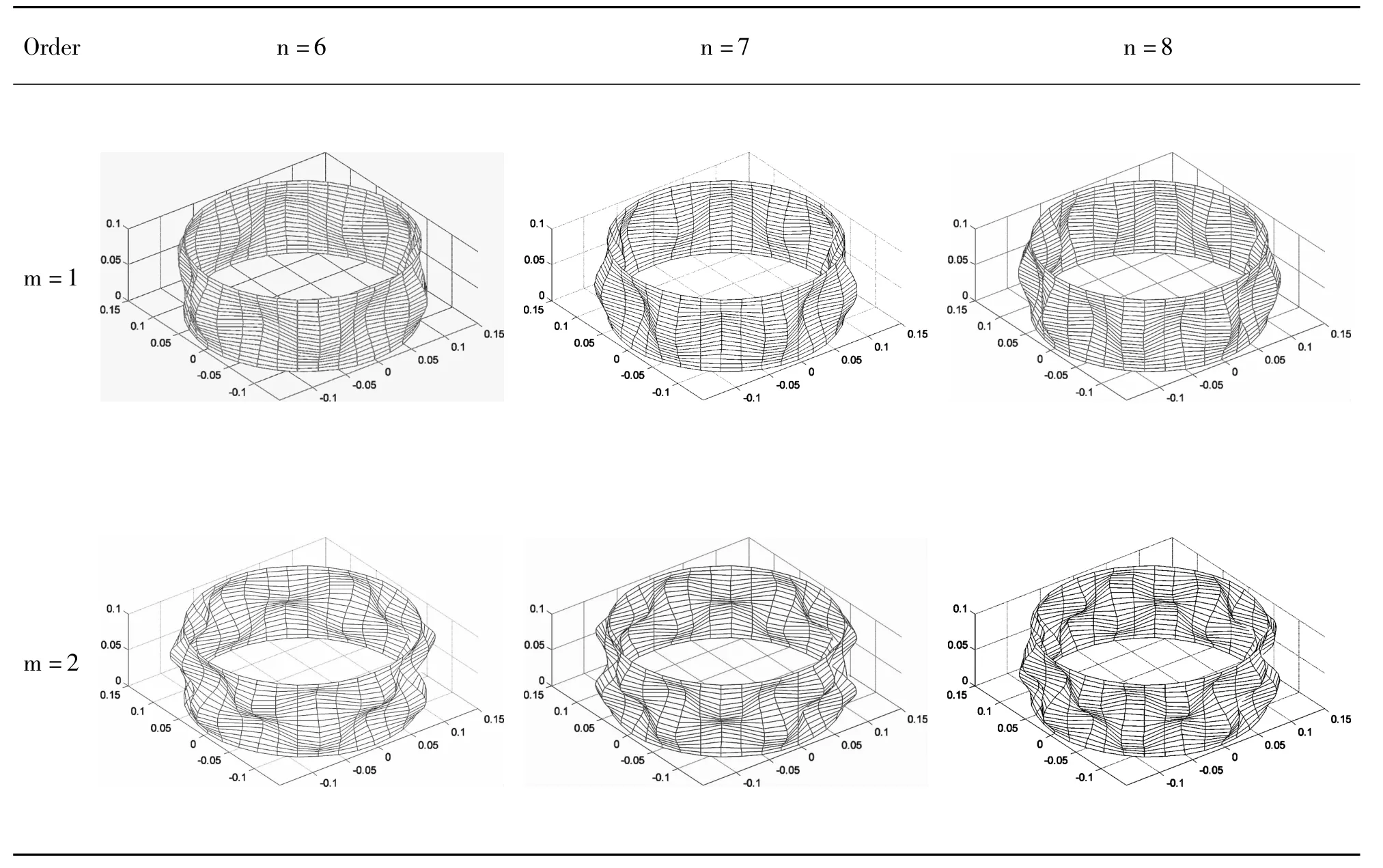
表3 固支-固支边界条件下薄壁圆柱壳的三维模态振型Table 3 modal shapes of a thin cylindrical shell under clamped-clamped boundary condition

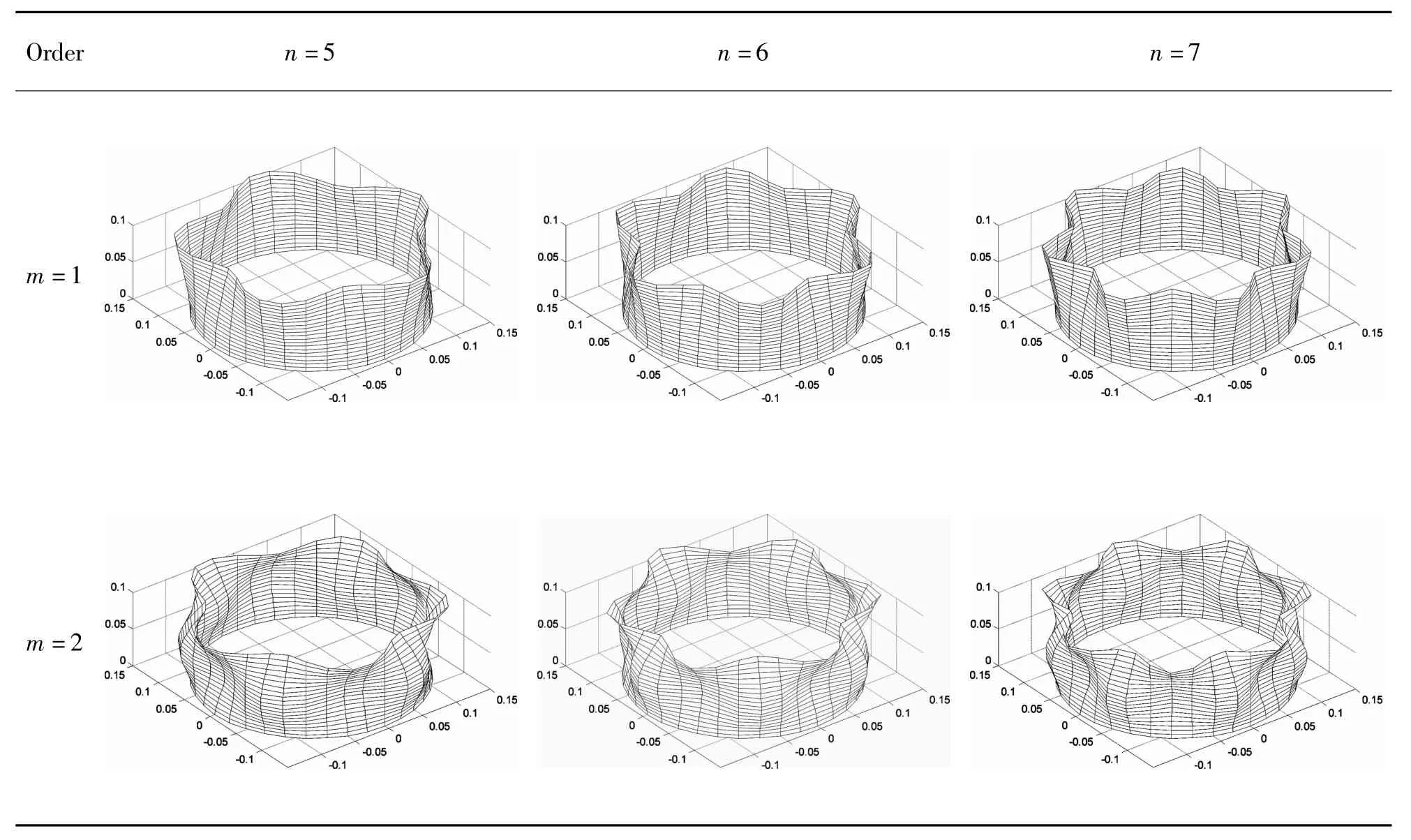
表4 固支-自由边界条件下薄壁圆柱壳的三维模态振型Table 4 3-D modal shapes of thin cylindrical shell under clamped-free boundary condition

（3）固支-自由边界条件

在固支-自由（即悬臂）边界条件下固有频率随周向波数和轴向半波数的关系曲线如图4所示，三维模态振型图如表4所示.可以看出，利用解析法求得的固有频率和简支-简支和固支-固支两种边界条件所求得的结果变化趋势相似，在低阶处的固有频率值先减小后增大，最小值出现在第（1，6）阶，对应的固有频率为1668Hz，在高阶时的固有频率随着周向波数的增加而逐渐升高；同时，随着轴向半波数的增大固有频率明显增加；如表4所示，固支-自由边界条件下的三维模态振型主要表现为自由端周向节点的振动，即悬臂端的振动位移最大，这是因为下端是固定的，对于圆柱壳有较强的约束作用，而对于上部约束影响较小，引起固有频率和模态振型发生相应变化；同时，固有频率最低的（1，6）阶对应的三维模态振型表现为周向波数为6的花瓣形状，是构件在服役过程中容易发生共振和产生故障的一阶模态，应当采取减振措施对振动进行预防和控制.

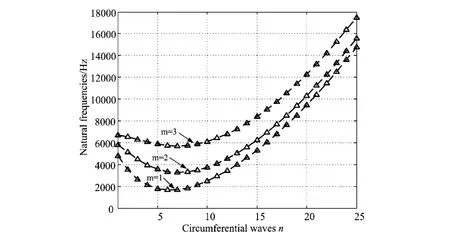
图4 固支-自由边界条件下薄壁圆柱壳的固有频率Fig. 4 Natural frequencies of a thin cylindrical shell under clamped-free boundary condition

3 结论

在简支-简支、固支-固支和固支-自由三种边界条件下，给出了求解薄壁圆柱壳高阶模态特性的解析法，利用文献和有限元法对结果进行了比较，算例结果表明：求得的固有频率值和文献与有限元法得到的结果变化趋势相同，固有频率的误差绝对值在2%以内；当周向波数较小时的固有频率先减小后增加，在高阶时的固有频率逐渐升高，当轴向半波数增加时固有频率依次增大，在简支-简支和固支-固支边界条件下的最低阶固有频率发生在第（1，7）阶，而固支-自由边界条件下的最低阶固有频率发生在（1，6）阶，最低阶模态也是构件在服役过程中最容易发生共振的一阶模态；同时，通过解析法和有限元法得到的三维模态振型吻合，主要表现为周向节点的振动，并且在低阶时以周向花瓣形状的振动模态为主，在高阶时出现轴向模态和周向模态的组合振型.

参 考 文 献

1 吴家龙.弹性力学.北京：高等教育出版社，2001（Wu J L. Elastic mechanics M. Beijing：Higher Education Press，2001（in Chinese））

2 Rongong J A，Tomlinson G R. Suppression of ring vibration modes of high nodal diameter using constrained layer damping methods. Smart Materials and Structures，1996，5（5）：672～684

3 Wang C，Lai J C S. Prediction of natural frequencies of finite length circular cylindrical shells. Applied Acoustics，2000，59（4）：385～400

4 El-Kaabazi N，Kennedy D. Calculation of natural frequencies and vibration modes of variable thickness cylindrical shells using the Wittrick-Williams algorithm. Computers & Structures，2012，104-105（4）：4～12

5 El-Mously M. Fundamental natural frequencies of thin cylindrical shells：a comparative study. Journal of Sound and Vibration，2003，264（5）：1167～1186

6 李国臣，李永强.薄壁圆柱壳固有频率的计算.机械科学与技术，2010，9（9）：1226～1229（Li G C，Li Y Q. Calculating natural frequencies of thin circular cylindrical shells. Mechanical Science and Technology，2010，9（9）：1226～1229（in Chinese））

7 杜长城，李映辉.功能梯度薄壁圆柱壳的自由振动.动力学与控制学报，2010，8（3）：219～223（Du C C，Li Y H. Free vibration of functionally graded cylindrical thin shells. Journal of Dynamics and Control，2010，8（3）：219～223 （in Chinese））

8 张爱国，李文达，杜敬涛等.不同边界条件正交各向异性圆柱壳结构固有振动分析.哈尔滨工程大学学报，2014，（4）：420～425（Zhang A G，Li W D，Du J T，et al. Natural vibration analysis of the orthotropic cylindrical shell structure with various boundary conditions. Journal of Harbin Engineering University，2014，（4）：420～425（in Chinese））

9 杨毅，魏光涛，阎桂荣.圆柱壳自由振动特性分析方法研究.应用力学学报，2011，28（1）：59～63，110（Yang Y，Wei G T，Yan G R. The research of vibration analysis methods for circular shell. Chinese Journal of Applied Mechanics，2011，28（1）：59～63，110（in Chinese））

10 陈正翔，陈维衡.圆柱壳中较高阶结构振动波的传播特性.华中理工大学学报，1997，（11）：93～95（Chen Z X，Zhang W H. Dispersion characteristics of higher orderstructural vibration waves in cylindrical shells. Journal of Huazhong University of Science and Technology，1997，（11）：93～95（in Chinese））

11 韩清凯，王宇，李学军.旋转薄壁圆柱壳的高节径振动特性以及篦齿结构的影响.中国科学：物理学、力学、天文学，2013，43（4）：436～458（Han Q K，Wang Y，Li X J. High nodal diameter vibration characteristics of rotating shell and the effects of its sealing teeth. Scientia Sinica Physica，Mechanica & Astronomica，2013，43（4）：436 ～458（in Chinese））

12 李晖，孙伟，许卓等.基于激光旋转扫描的约束态薄壁圆柱壳模态振型测试新方法.振动与冲击，2014，33 （16）：155～159（Li H，Sun W，Xu Z，et al. Experimental method of laser rotating scanning to measure mode shapes of constrained thin cylindrical shell. Journal of Vibration and Shock，2014，33（16）：155～159（in Chinese））

13 陈丽华，孙玥，张伟.三阶剪切变形板的振动特性研究.动力学与控制学报，2014，12（1）：50～55（Chen L H，Sun Y，Zhang W. Study on vibration characteristic of third order shear deformation theory of plate. Journal of Dynamics and Control，2014，12（1）：50～55（in Chinese））

14 Soedel W. Vibrations of shells and plates. CRC Press，2004

15 洪杰，郭宝亭，朱梓根.高速转动壳体行波振动实验研究.航空动力学，1998，13（4）：390～394（Hong J，Guo B T，Zhu Z G. Experimental investigation on travelling wave vibration of high-speed rotating shell. Journal of Aerospace Power，1998，13（4）：390～394（in Chinese））

Received 04 December 2014，revised 27 December 2014.

*The project supported by the National Natural Science Foundation of China（51105187）and Research Fund for Young Teachers of University of Science and Technology Liaoning（2014QN13）

STUDY ON VIBRATION CHARACTERISTICS OF HIGH-ORDER MODAL FOR A THIN CYLINDRICAL SHELL*

Wang Yu1†Luo Zhong2Li Chang1Liu Jian1
（1. School of Mechanical Engineering，University of Science and Technology Liaoning，Anshan 114051，Liaoning China）（2. School of Mechanical Engineering，Northeast University，Shenyang 110819，China）

AbstractThe vibration characteristics on a high-order modal of a thin cylindrical shell is studied in this paper by analytical method under different boundary conditions. Firstly，the shell dynamics model is established by Galerkin′s method based on Love′s shell theory under simply supported-simply supported，clamped-clamped and clamped-free boundary conditions. Secondly，the modal characteristics are solved，and the high-order natural frequencies as well as three-dimensional mode shapes are obtained. Finally，the results are compared with the data from the related literature and finite element method. The results show that the error values of natural frequencies using analytical method are less than 2%for the shell under simply supported boundary condition at both ends. The natural frequency increases after the first decrease when circumferential wave numbers are small，while it increases gradually when circumferential wave numbers are higher，but the natural frequencies increase significantly when axial half-wave numbers rise. Moreover，the three-dimensional modal shapes obtained from the analytical method，related literature and finite element method are coincident.

Key wordsthin cylindrical shell， boundary condition， high-order natural frequency， three-dimensional modal shape

DOI：10. 6052/1672-6553-2015-012

通讯作者†E-mail：wangyu435@126. com

Corresponding author†E-mail：wangyu435@126. com