细长柔性空间结构几种动力学模型的比较*

赵国威吴志刚，2†

（1.大连理工大学工业装备结构分析国家重点实验室，大连 116024）（2.大连理工大学航空航天学院，大连 116024）



细长柔性空间结构几种动力学模型的比较*

赵国威1吴志刚1，2†

（1.大连理工大学工业装备结构分析国家重点实验室，大连 116024）（2.大连理工大学航空航天学院，大连 116024）

摘要对于自由-自由边界的大型柔性梁式空间结构在轨搬运过程中，其大范围刚体运动和柔性振动会相互耦合，是一类典型的刚柔耦合动力学问题.建立相对准确的动力学模型是设计良好控制系统的前提，但现有文献在研究该问题时却采用了忽略刚柔耦合作用的动力学模型并依此设计控制器，因此有必要建立耦合模型，并探讨其与非耦合模型之间的区别和适用性.首先针对结构自身运动特点选择以瞬时质心为原点的浮动坐标系作为辅助坐标系，将结构两类不同的运动形式进行分解，并利用其产生的附加约束条件简化虚功表达式；其次选择Euler-Bernoulli梁变形形式描述结构变形并采用假设模态法对变形进行变量分离；基于虚功原理推导得到结构大范围运动的刚柔耦合动力学模型；通过仿真算例1对非耦合模型、零次近似模型和一次近似模型进行了对比，验证了非耦合模型的不合理性及零次近似简化模型的准确性和有效性；通过仿真算例2对零次近似简化模型和一次近似模型的对比，说明了二者的使用范围；仿真对比为后续的运动控制系统设计和振动抑制研究提供了依据.

关键词柔性空间结构， 在轨搬运， 浮动坐标系， 刚柔耦合， 自由-自由边界

2014-04-17收到第1稿，2014-07-31收到修改稿.

*国家自然科学基金资助项目（11432010，11072044）、高等学校博士学科点专项科研基金（20110041130001）、教育部新世纪优秀人才支持计划（NCET-11-0054）

引言

未来空间战略发展会对空间结构提出一些新的需求，诸如应对能源枯竭的大型空间太阳能电站、有助于向宇宙深处进军的深空探测平台等的构建，这些结构都体积巨大，可达几千米甚至于几十千米，需要通过子结构在轨搬运装配这一特殊方式来完成构造搭建［1，2］.这些子结构通常都是柔性梁式桁架结构，其轴向尺寸（几十米甚至几百米）远大于其横向尺寸（几米），因此明显具有质量小、体积大、频率低等特点.桁架梁结构的在轨搬运过程是一种大范围机动作用，很容易诱发结构的柔性振动，这样结构刚体运动和柔性振动就会互相耦合互相影响，可见空间柔性结构在轨搬运过程是一类比较典型的刚柔耦合系统动力学问题.

此类问题早期的建模方法是独立分析刚体运动和柔性振动，不考虑两者的耦合作用；之后出现零次近似模型建模方法，仅简单考虑了刚体运动和柔性振动的耦合影响. 1987年，Kane［3］通过对悬臂梁变形的详细描述，建立了一次近似模型，最后指出了零次近似模型的缺陷，并首次提出“动力刚化”概念.之后，该问题开始引起广大学者的广泛关注. Canavin［4］探讨和总结了柔性航天器作大范围运动建模过程中的浮动坐标系选择问题，概括了五种选择方法，并详细描述了它们各自的特点. Zeller［5］、Waszak［6］等利用平均轴坐标系（Mean Axes）建立了无约束柔性体耦合动力学模型，但仅是零次近似模型. Li［7］等分别利用平均轴坐标系和固定轴（Fixed Axes）坐标系对柔性飞行器的动力学建模问题进行了研究，通过对两者的仿真对比，认为它们差别不大，但后者结果更精确. Li［8］等利用连体坐标系（Body-Fixed）对飞艇飞行过程进行了动力学建模和仿真，分析了空气动力学对结构动力学特性的影响. Huang［9］等利用平均轴坐标系和传统的零次近似描述针对变质量火箭结构飞行过程中的刚柔耦合建模问题进行了研究. Nikravesh［10 -12］探讨了关于运动柔性体建模过程中浮动坐标系的选择问题，主要针对惯性主轴（Principal Axes）、固定节点（Node-Fixed Axes）和平均轴三种坐标系所附带的约束方程及对变形的描述等问题进行了分析说明. Shi［13］等深入研究分析了柔性Euler-Bernoulli梁的变形问题，充分考虑横向、纵向变形之间的耦合影响，给出了精确的非线性变形描述.洪嘉振［14，15］对刚柔耦合问题进行了全面的阐述和讨论，推导了一次近似模型，深入探讨了“动力刚化问题”并从实验方面进行了验证.蒋丽忠［16，17］等针对固结在刚体上的大范围转动柔性悬臂梁、板的刚柔耦合建模问题、动力特性和稳定性等问题进行了研究，通过对比给出了传统零次模型的缺陷及一次近似模型的优势.吴胜宝［18］等针对作平面运动的悬臂梁建立了一次近似耦合模型，并针对其与零次模型之间的区别进行了探讨.黎亮［19］等对作大范围运动的悬臂功能梯度矩形薄板的刚柔耦合问题进行了研究，考虑了传统零次模型建模方法中忽略的横向弯曲作用对纵向变形的影响，仿真比较了两种模型的差异.刘锦阳［20］等针对柔性梁刚柔耦合问题，基于绝对节点坐标法研究了几何非线性和一次近似模型在大变形问题中的适用性.以上研究大部分是针对中心刚体-柔性附件结构，一般都采用局部附着坐标系（Locally Attached Frame）作为浮动坐标系，直接建立在刚体上；也有些研究是针对无约束柔性结构，但对本任务有如下一些问题：1）选择结构端部作为浮动坐标系原点，不利于使用质心约束条件；2）平均轴坐标系附带的约束条件太强，一般很难满足，直接使用的做法明显欠妥；3）采用有限元离散导致自由度数目较大，不利于后期控制系统设计.

柔性空间结构在轨搬运过程中的刚柔耦合作用，会产生两方面的问题：一是柔性振动使得推进装置随之发生抖动，导致推进力方向不断变化，从而造成燃料的过多消耗，降低了使用效率；二是受机动作用的影响，当结构机动到达期望位置时，柔性振动不能得到有效抑制，残余振动在很长一段时间难以被消除，由于难以锁定结构位置导致装配机器人无法完成抓取动作，从而严重影响装配工作的顺利开展，极大降低工作效率.建立合理的搬运过程动力学模型，有利于对结构的残余振动行为进行预测，这样可以据此设计相应的柔性结构运动控制系统，达到提高燃料使用率和抑制残余振动的目的. Boning［1］、Ishijima［2］等对空间结构在轨搬运问题进行了结构运动研究，但其研究工作均是基于非耦合动力学模型，并未针对非耦合模型和耦合模型的差别进行的探讨分析，因此选择非耦合模型是否足够合理还是非常值得探讨的，这将会对后续的运动控制系统设计起到至关重要的作用.

1 运动学描述

1. 1 浮动坐标系

细长柔性空间结构通常为桁架梁形式，理论分析中多采用连续梁模型进行处理.考虑如图1所示系统，柔性梁作平面运动. XOY为全局惯性坐标系，xfofyf为浮动坐标系，在初始时刻两坐标系重合.图中实线表示柔性梁任意时刻变形位置；虚线表示该时刻假想的梁未变形时的位置. xfofyf的选择如下：对任意时刻t，选择梁未变形时的质心位置作为浮动坐标系原点of，该点是与梁变形后质心相重合的空间点的位置，注意它并非材料点位置，而是一个瞬时质心；ofxf与梁未变形时的轴线平行，初始向右为正；ofyf与横向平行，初始向上为正.平面梁的密度用γ表示，横截面积用F表示，质量用Mb表示，长度用L表示，体积用V表示，弹性模量用E表示，横截面惯性矩用I表示.

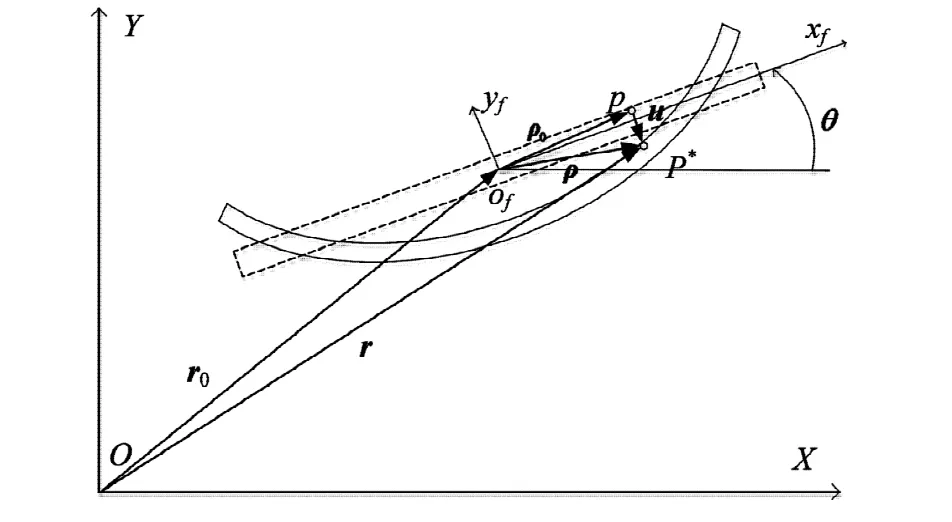
图1 平面梁的位移描述Fig. 1 Displacement description of planar beam

图中各量物理意义如下：p为未变形时梁上任意一点；p*为变形后与p所对应的点；r0为浮动坐标系原点相对于惯性坐标系的位移向量，用来表征梁的大范围平动；θ为浮动坐标系相对于惯性坐标系的旋转角度，以逆时针为正，用来表征梁的大范围转动；ρ0为点p在浮动坐标系中的位置向量，在浮动坐标系下描述，是材料点坐标函数；u为p*相对于原位置p产生的变形量，在浮动坐标系下描述，是材料点坐标和时间的函数；r为p*点在全局惯性坐标系下的绝对位移向量，其表达式可写为

上式中r0=（xbyb）T，ρ0=（x y）T，u =（u1u2）T，其中ρ0中的y在细长梁中可忽略不计，因此后文中直接以零计；A是旋转变换矩阵，形式如下

通过式（1）对时间求导，得到p*点在全局惯性坐标系下的速度表达式

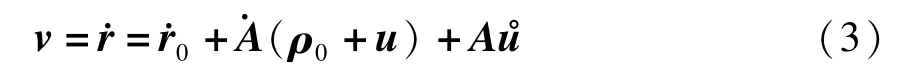
上式中，“·”表示在惯性系下对时间求导；“°”表示在浮动坐标系下对时间求导；同时有

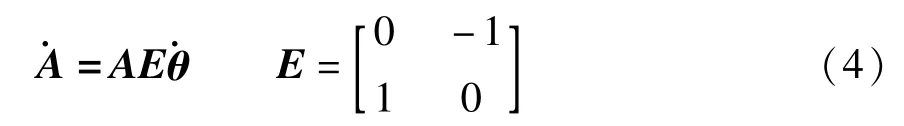
同样的，由式（3）对时间求导，可得到p*点的绝对加速度表达式

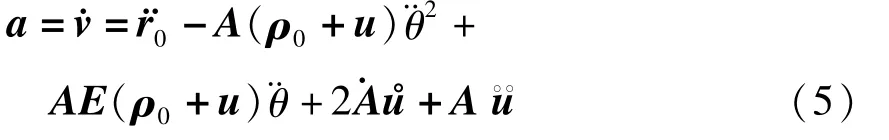
根据前面对浮动坐标系原点的定义，可以得到如下质心约束条件

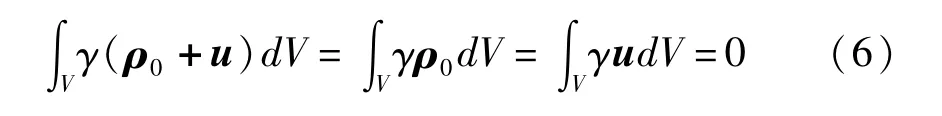
上式在浮动坐标系下对时间求导，可以得到线动量约束条件

若将浮动坐标系原点选择在结构端点是不具备这样的约束条件的，约束条件式（6）和（7）对后面利用虚功原理进行动力学方程的简化推导有着很重要的作用.

1. 2 变形描述

对于这样的细长梁，通常采用Euler-Bernoulli柔性梁的变形理论描述，忽略横截面的影响，可以将任意一点p的变形用与其相对应的同横截面轴线上的点p0的变形来描述.变形的一次近似关系可表示如下

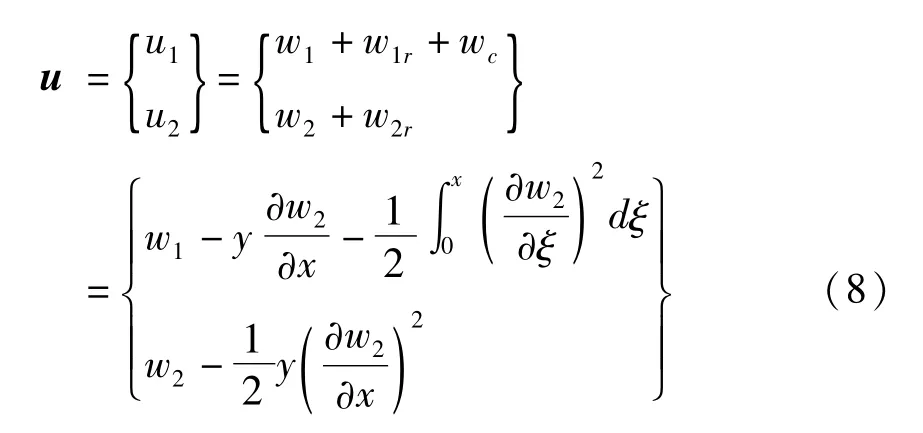
其中，u1表示p点的纵向变形位移，u2表示p点的横向变形位移；w1表示p0点的轴向伸缩变形位移，w1r是由于横截面转动引起的p点相对于p0点的纵向变形位移；wc是由于横向弯曲变形而造成的纵向伸缩量，是一个耦合项，同时也是一次近似模型和传统零次近似模型最重要的区别；w2表示p0点的横向弯曲变形位移；w2r是由于横截面转动引起的p点相对于p0点的横向变形位移，对于细长梁而言，此项相对于w2可忽略，后面推导中不计此项.

2 刚柔耦合动力学方程

2. 1 惯性力所作虚功

选取如下广义状态向量

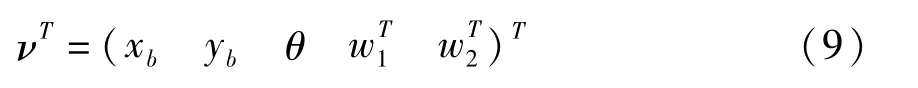
由式（1）和（8），结构的虚位移表示为

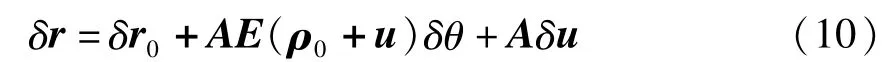
其中

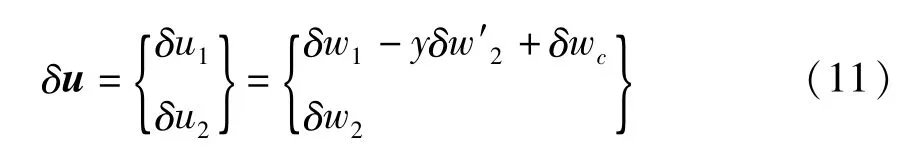
结构惯性力在虚位移上所作的虚功为

上式中的单下划线项在区间上的积分为零，这可由前面的质心约束条件和线动量约束条件很容易得到.这正是对于自由-自由梁结构，选择瞬时质心而非结构端点作为浮动坐标系原点所带来的优势，为理论推导带来了方便，简化了后续运算.

将式（11）带入（12），得到

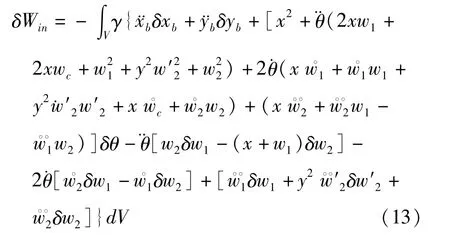
由于wc本身为小量，因此上式中仅保留其一次项，如w1wc、w2wc、wc2等被忽略.

2.2 外力所作虚功

选取与状态向量相对应的外力

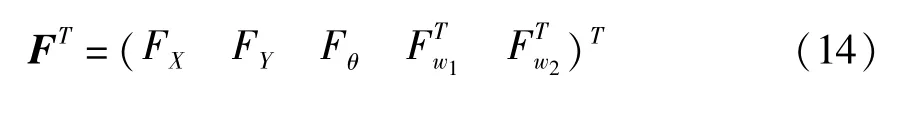
其中FX、FY是合外力主矢在全局惯性坐标系中X、Y方向上的投影；Fθ是合外力关于梁结构质心的主力矩；Fw1和Fw2是分别对应纵向和横向变形的外力主矢分量，则外力所作虚功表示为

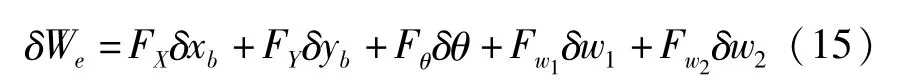
2. 3 虚应变能

对于Euler-Bernoulli梁，不考虑剪切和扭转，梁上任意点纵向正应变可表示为

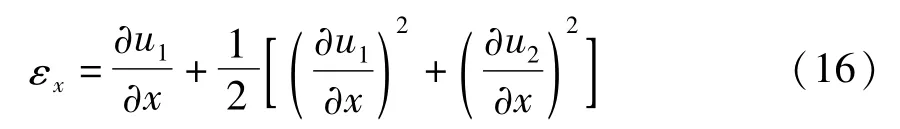
假定梁处于线弹性范围，将式（8）带入并整理，仅保留轴向伸缩应变能和横向弯曲应变能，得到

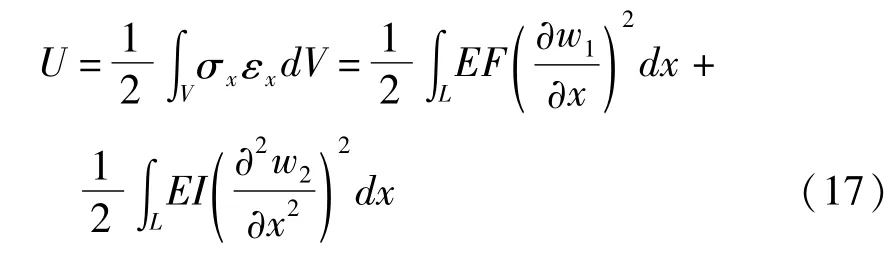
式中I为横截面抗弯刚度，表达式为

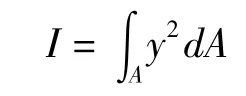
由虚位移引起的结构应变能改变为

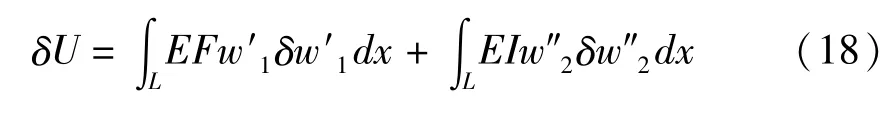
2. 4 分离变量

由于变形量w1和w2不仅是时间的函数，还是材料坐标的函数，属于二元函数，只能得到偏微分形式的动力学方程，很不利于方程的求解和分析.通常需要对其进行变量分离处理：假设模态法和有限元法.有限元可以模拟各种复杂形状和特殊边界的结构，并且相对直观，程式化好，但自由度数目太大，不利于后续控制系统的设计，因此这里选择假设模态法进行变量分离.

取梁上任意点的轴向变形w1和横向变形w2有如下分离变量形式

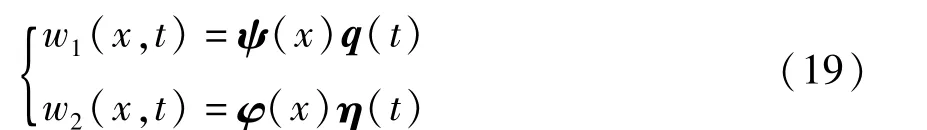
式中，ψ∈R1×n和φ∈R1×n分别是梁纵向振动和横向振动的振型函数矢量，q∈Rn×1和η∈Rn×1分别对应于梁纵向振动和横向振动的模态坐标函数矢量.对于自由-自由边界梁，各阶振型函数可取为

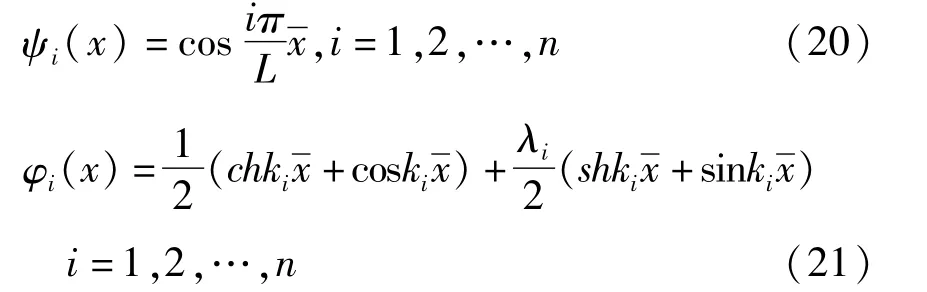
其中ki是chkiLcoskiL =1的第i个根

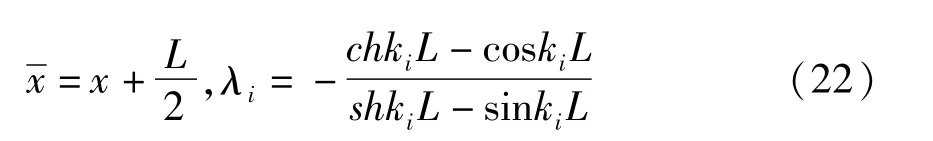
由式（19）可以得到式（11）、（15）和（18）中各变形相关量的变分为

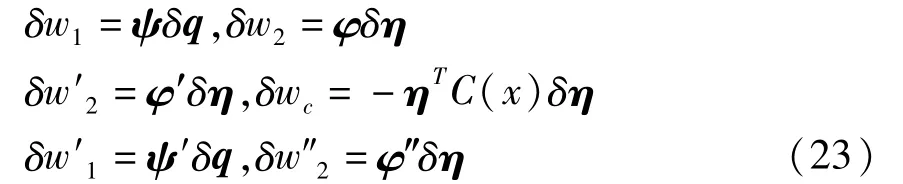
2. 5 动力学方程

运用虚功原理

其中，δU、δWe、δWin分别是虚位移引起的结构应变能的改变、外力在虚位移上所作的虚功和惯性力在虚位移上所作的虚功.

将式（13）、（15）、（18）和（23）代入到式（24）并整理，得到自由-自由边界柔性梁的一次近似刚柔耦合动力学模型

其中各元素的具体表达式如下

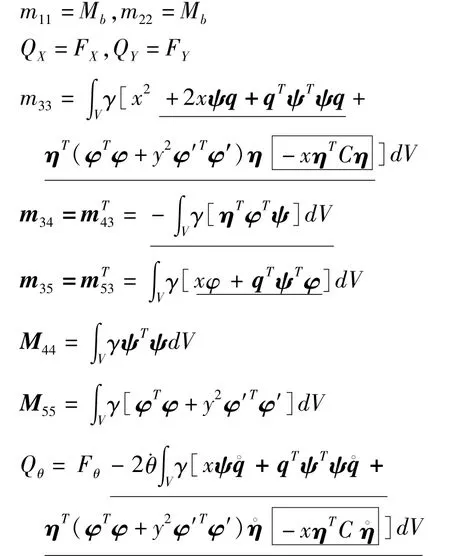
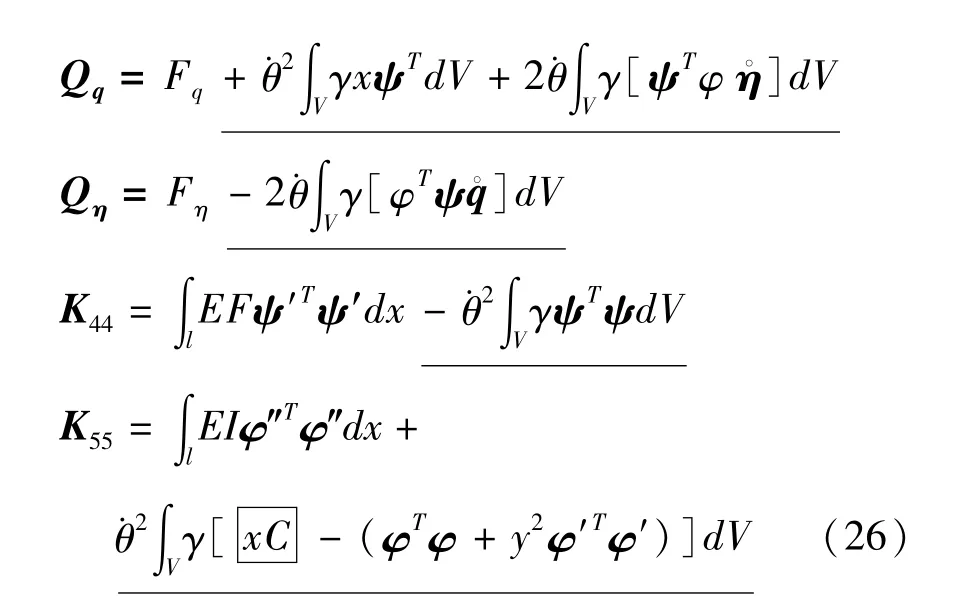
从式（25）、（26）可以看到：对于自由-自由无约束柔性梁在经历大范围运动过程中，其刚体平动运动并不与柔性振动发生相互耦合作用；柔性振动仅与大范围转动相互耦合，柔性振动的刚度项也仅与转动速度有关而与平动无关.对上面表达式进行不同程度的简化可得到如下四种模型：1）非耦合模型，去掉有下划线的项可得，文献［1，2］采用的就是该模型；2）零次近似模型，仅去除带实线方框的项可得，“动力刚化”被提出之前采用该模型；3）零次近似简化模型，去除零次近似模型中的轴向变形方程可得，即令w1=0；4）一次近似模型.从表达式可以看到：后三种均为耦合模型，其轴向和横向的刚度与大范围转动速度有关，因此其频率也与结构动力学中的固有频率意义不同；随着结构转动角速度的增加，零次近似模型的刚度会变成负值，导致发散解，这是不符合实际的；一次近似模型由于考虑了横向变形对纵向变形的影响，即wc项的存在，使得横向弯曲刚度恒大于零，但其轴向刚度却随着转动角速度的增加而减小，最终变成负值.

3 对比验证

由前面的分析知道：结构横向弯曲刚度仅与转动速度有关，故将零次近似模型弯曲刚度为零时的转速作为临界转速，分别在低转速和临界转速两种情况下，针对前面所述的几种模型，对它们的运动轨迹进行仿真，通过对比说明它们之间的不同.仿真计算全部基于Windows 7. X64位操作系统下的大型数值计算软件Matlab进行.根据文献［1，2］选取如下典型的结构相关参数：梁长L = 200m，质量为Mb=600kg，均匀分布，截面尺寸为1m×1m，弹性模量E =181. 72MPa，临界转速为˙θ=1. 2566rad/ s.

对比1：低转速情况.在轨搬运过程有其特殊的工作环境，一般来讲，其运动速度都很小，故此情况下选择文献［1，2］中的非耦合模型以及本文前面介绍的零次近似简化模型和一次近似模型进行仿真，通过结构在给定载荷作用下两端点的运动轨迹曲线的对比，分析非耦合模型和耦合模型之间的差距，并说明哪一种模型更适合作为运动控制系统设计时的参考模型.

假设期望位置和期望时间分别用Xm、Ym、θm、Te表示，则整定轨迹如下表示

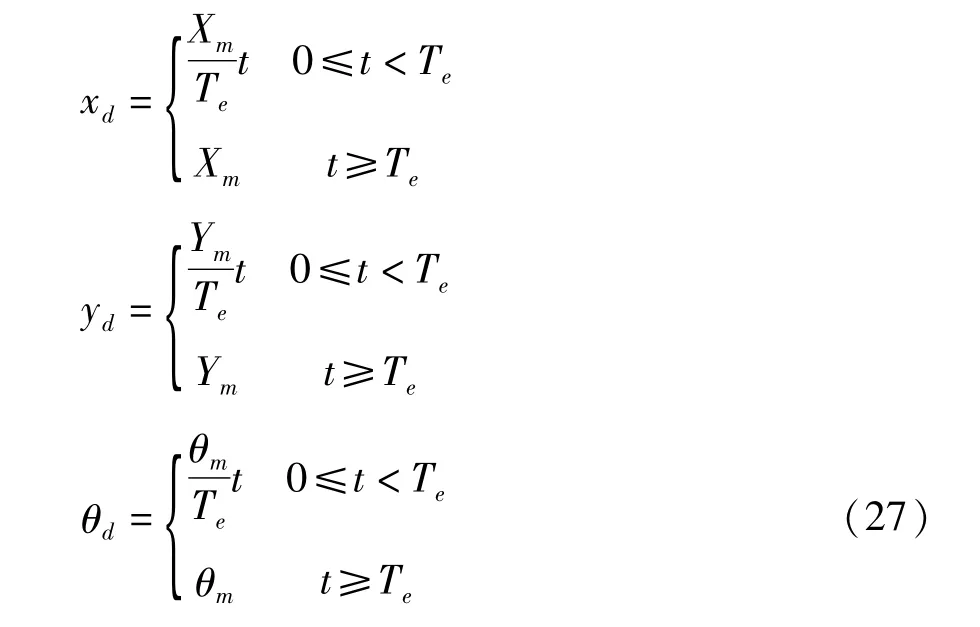
取Xm=200m、Ym=200m、θm=π/2、Te=200s，则结构左、右端点的初始位置分别为：（- 100，0）、（100，0）；在该设计载荷作用下的最终位置应分别为：（200，100）、（200，300），三种模型的仿真轨迹曲线对比如图2～图3.

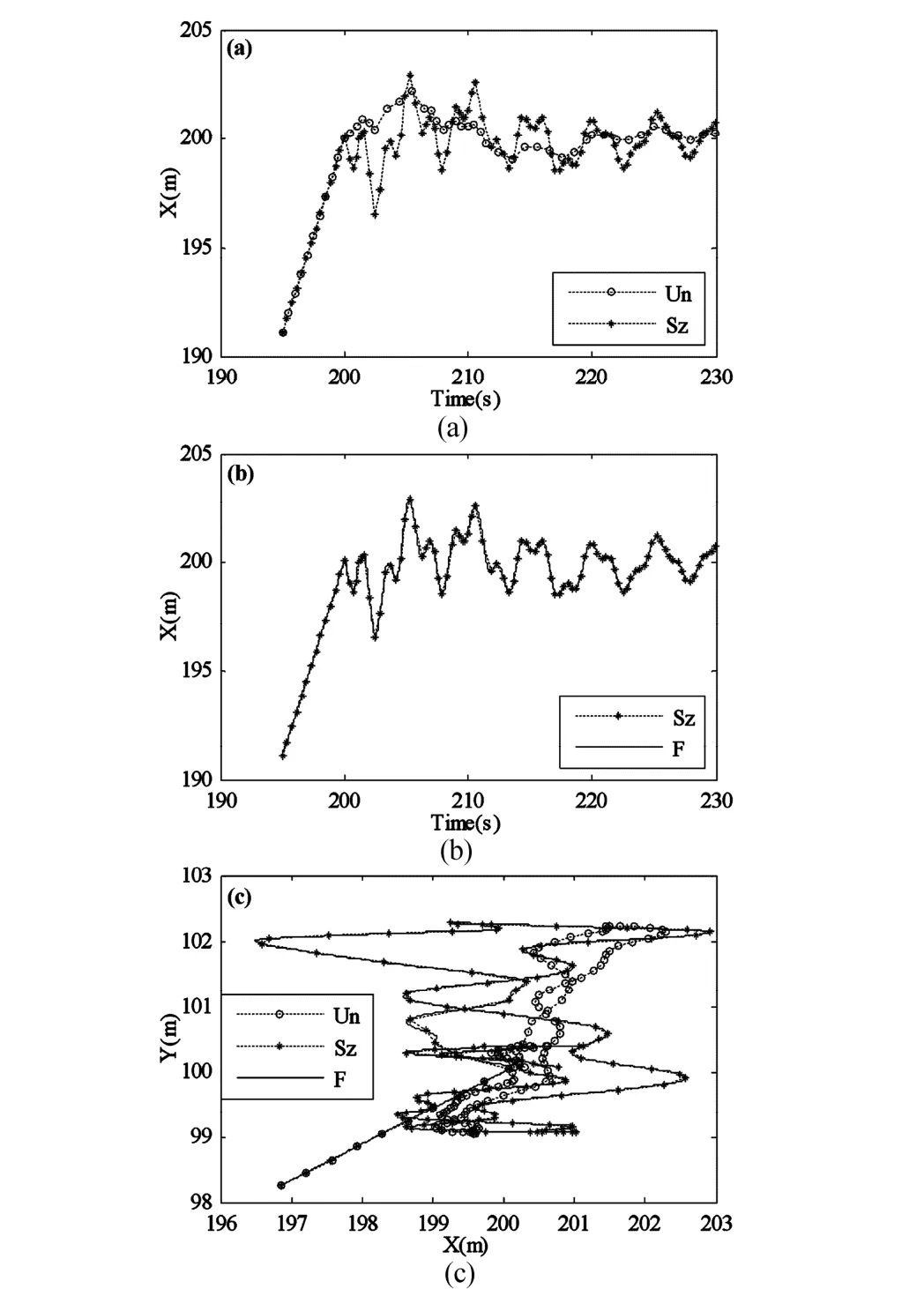
图2 左端点轨迹曲线Fig. 2 Trajectories of left endpoint

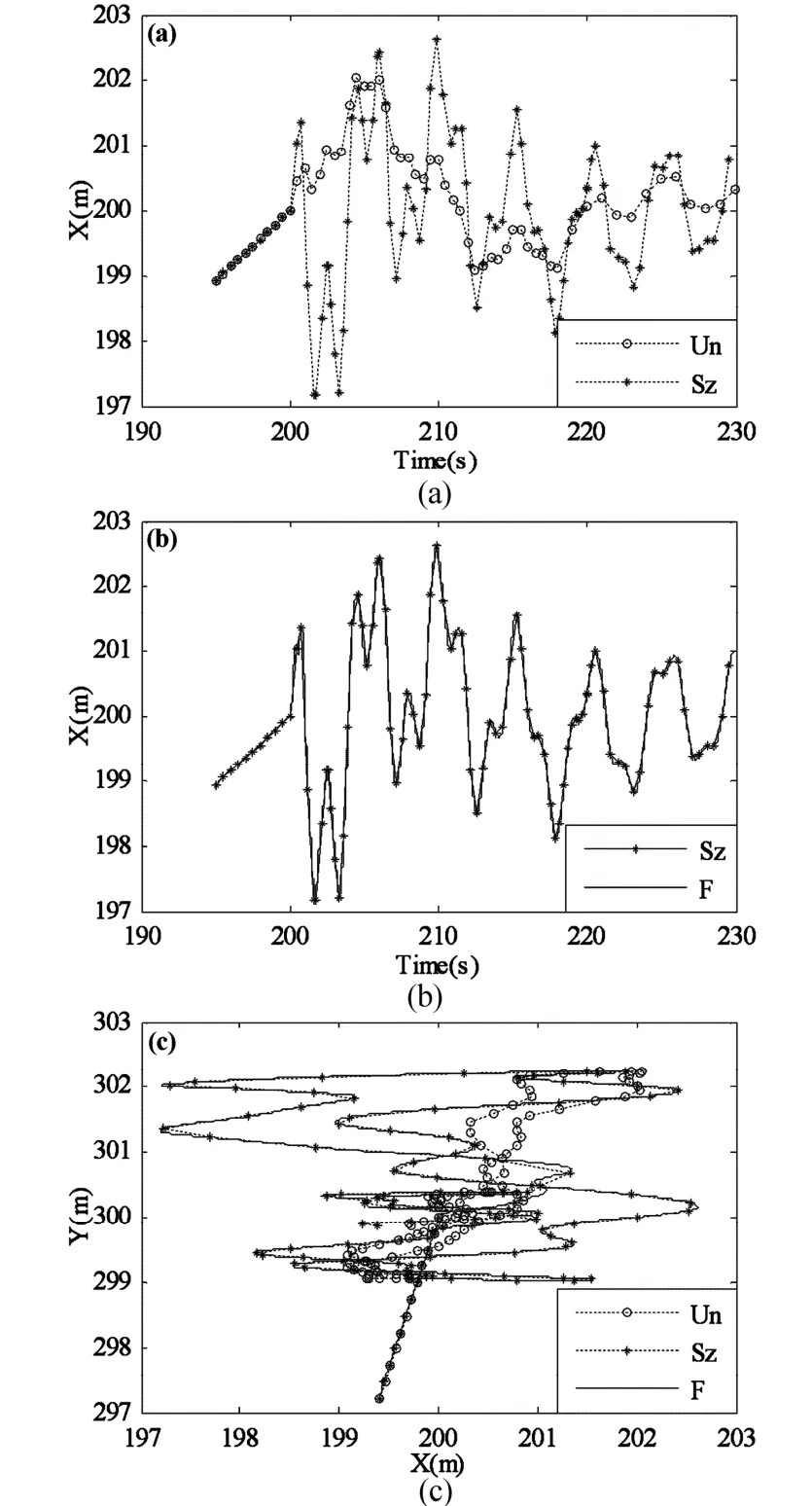
图3 右端点轨迹曲线Fig. 3 Trajectories of right endpoint

图2～图3表示结构左、右端点到达期望位置附近的局部放大图，选取时间间隔为195～230s.由于到达期望位置时，图中的X方向与结构横向弯曲方向一致，而Y方向与结构纵向振动方向一致，因此仅给出X方向位置-时间曲线（如图（a）、（b））和X-Y方向轨迹曲线（图（c））.图中“Un”代表非耦合模型，“Sz”代表零次近似简化模型，“F”代表一次近似模型.从图（a）中可以看到：非耦合模型与零次近似简化模型位置偏差较为明显.从图（b）中可以看到：零次近似简化模型与一次近似模型的位置偏差极小，可以认为两者一样.从图（c）中可以看出，非耦合模型、零次近似简化模型和一次近似模型均能到达指定位置；但三种模型下结构端点到达期望位置后都会出现一些残余振动，其中非耦合模型端点轨迹变化保持在199～202m，残余振动范围约为2～3m；零次近似简化模型和一次近似模型结果相对比较一致，端点轨迹变化范围保持在197m～203m，残余振动范围约为5～6m；非耦合模型结果明显偏小，说明其不能准确地描述结构动力学行为.非耦合模型之所以有这样的结果正是其没有考虑刚柔耦合作用的影响，对模型处理得过于简单而导致，文献［1，2］直接采用该模型进行运动控制系统设计很明显是不合适的，应当采用耦合模型.

刚柔耦合模型在数值计算时，会遇到“刚性”问题而降低计算效率，零次近似简化模型由于耦合较弱，所以计算效率会远远高于一次近似模型，其仿真结果却又能和一次近似模型保持一致.通过以上分析，可以知道对于在轨搬运过程这类低速运动情况下，采用零次近似简化模型要优于非耦合模型和一次近似模型.

对比2：临界转速情况.从式看到零次近似模型的刚度随着转速增大而减小，而一次近似模型的刚度随着转速增大而增大，两者有较大差异.此算例用来验证零次近似简化模型、零次近似模型和一次近似模型三种耦合模型在临界转速附近会有那些不同，对大范围运动会造成哪些影响.

给出如下旋转力矩，结构在其作用下角速度会从零增加至某一恒定值然后保持匀速转动，其中fac表示恒定转速与临界转速的比值.结构左端点、中间点和右端点的初始位置分别为：（- 100，0）、（0，0）、（100，0），加载至恒转速后，中间点保持不动仍为（0，0），两端点围绕中间点作周期性圆周运动，其轨迹为以（0，0）为圆心，以100为半径的圆.三种模型的仿真轨迹曲线对比如图4～图6.

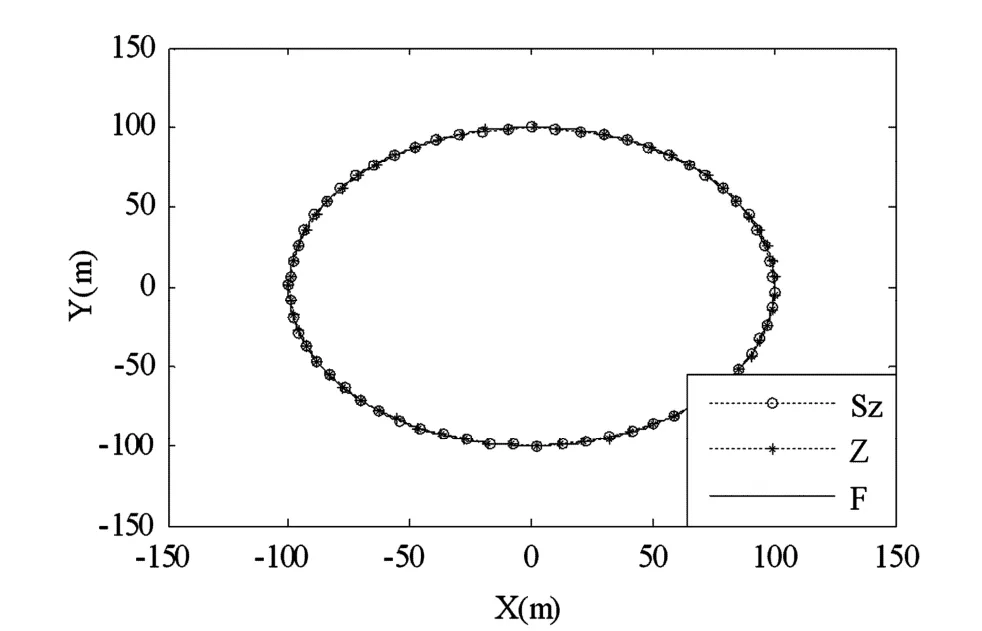
图4 左端点轨迹曲线Fig. 4 Trajectories of left endpoint

图4～图6是当fac =0.8时结构达到恒速后左端点、中间点和右端点的运动轨迹曲线.横坐标表示X方向位置，纵坐标表示Y方向位置.图中“Sz”代表零次近似简化耦合模型，“Z”代表零次近似模型，“F”代表一次近似模型.可以看出，当结构转速接近于临界转速时，零次近似简化模型和零次近似模型的结果与一次近似模型的结果依然是吻合的，并且结构运动轨迹符合预期的周期性圆周运动并保持稳定，由此可见，由转速引起的刚度变化并没有对大范围运动带来明显影响.

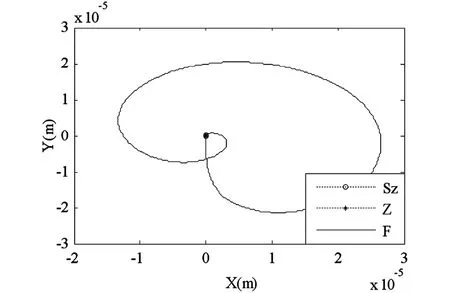
图5 中间点轨迹曲线Fig. 5 Trajectories of midpoint

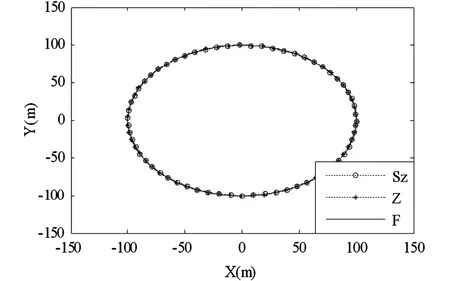
图6 右端点轨迹曲线Fig. 6 Trajectories of right endpoint

图7～图9是当fac = 1. 2时结构达到恒速后左端点、中间点和右端点的运动轨迹曲线.横坐标表示X方向位置，纵坐标表示Y方向位置.图中“Sz”代表零次近似简化耦合模型，“Z”代表零次近似模型，“F”代表一次近似模型.可以看出，当结构转速超过临界转速后，零次近似简化模型、零次近似模型运动轨迹基本保持一致，但两者均出现了较大的波动，偏离了预期的圆周轨迹，失去周期性，变得不稳定，有发散的趋势，不符合基本物理事实；而一次近似模型的运动轨迹与预期的圆周运动相吻合，呈现周期性和稳定性的特点，与实际情况相符.究其原因，零次近似简化模型和零次近似模型的刚度随着转动角速度的增大而减小，超过临界转速后会变成负值，使得结构横向弯曲振动发散，最终导致大范围运动的失稳；而一次近似模型的刚度会随着转动角速度的增大而增大，这正是Kane［3］所指出的“动力刚化”现象.可见当转速达到并超过临界转速的情况下，应采用一次近似模型作为系统的刚柔耦合动力学模型.当然，关于零次近似简化模型的适用范围的精确阐述和研究不在本文讨论范围之内.

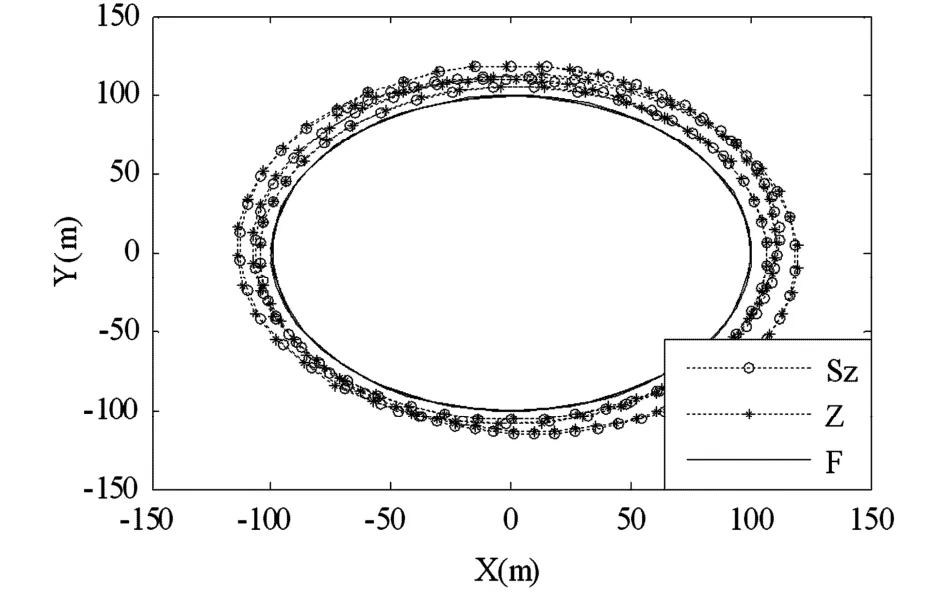
图7 左端点轨迹曲线Fig. 7 Trajectories of left endpoint

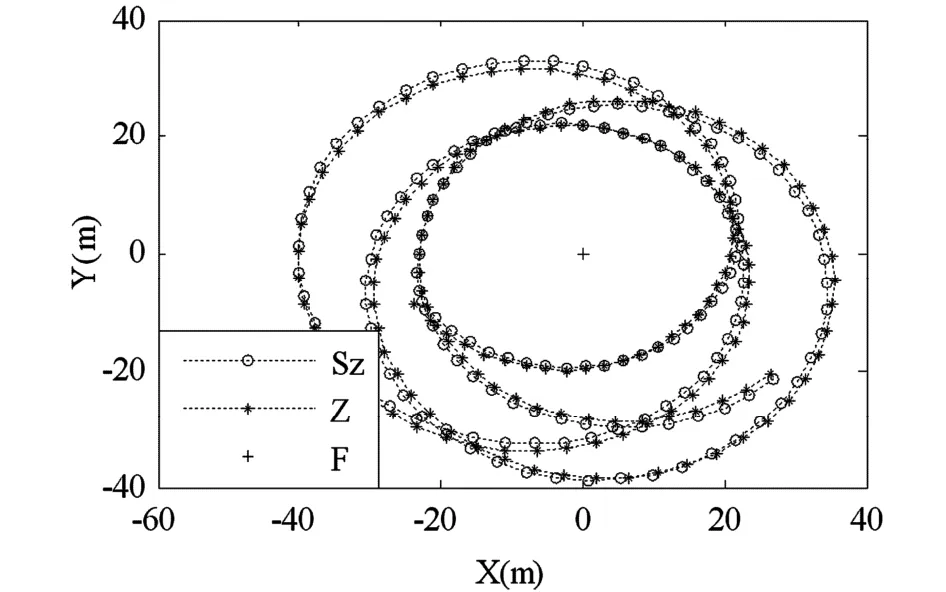
图8 中间点轨迹曲线Fig. 8 Trajectories of midpoint

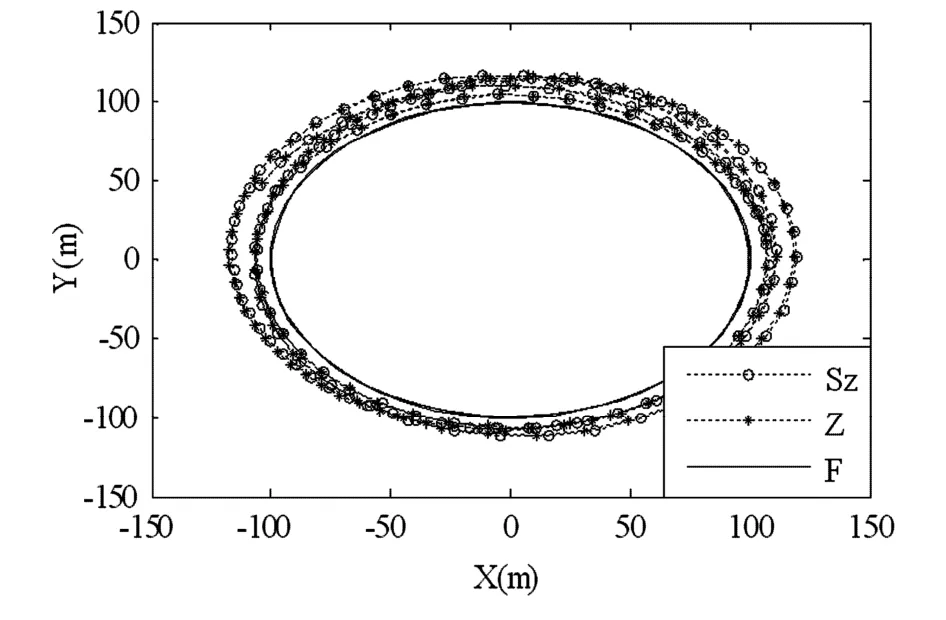
图9 右端点轨迹曲线Fig. 9 Trajectories of right endpoint

4 结论

基于浮动坐标系对柔性空间结构在轨搬运过程的刚柔耦合动力学问题进行了研究，建立了自由-自由边界细长柔性空间梁大范围运动的几种动力学模型，通过与文献［1，2］中的非耦合模型及不同转速情况下的仿真对比，可得到以下几个结论：（1）在轨搬运过程中采用非耦合模型的结果是不准确的，依此设计运动控制系统的效果令人质疑；（2）在轨搬运过程可采用零次近似简化模型，比非耦合模型结果更准确可靠；（3）耦合模型的刚度与大范围平动无关，仅与大范围转动有关，与结构动力学意义下的刚度有本质区别；（4）一次近似模型比零次近似模型更为准确地描述了耦合效应的本质；（5）零次近似模型的适用范围和结构转速有关，但不能简单的仅通过临界转速进行判断.上述对比结果为细长柔性空间结构在轨装配过程运动控制系统设计提供了依据.

参 考 文 献

1 Boning P. The coordinated of space robot teams for the onorbit construction of large flexible space structures［PhD Thesis］. Cambridge：Massachusetts Institute of Technology，2009

2 Ishijima Y，Tzeranis D，Dubowsky S. The on-orbit maneuvering of large space flexible structures by free-flying robots. In：Battrick B ed，ESA SP-603，Proceedings of the 8th International Symposium on Artificial Intelligence，Robotics and Automation in Space. Munich，Germany：European Space Agency，2005

3 Kane TR，Ryan R R，Banerjee A K. Dynamics of cantilever beam attached to moving base. Journal of Guidance，Control and Dynamics，1987，10（2）：139～151

4 Canavin J R，Likins P W. Floating reference frame for flexible spacecraft. Journal of Spacecraft，1977，14（12）：724～732

5 Zeller T A，Buttrill C S. Dynamic analysis of an unrestrained，rotating structure through nonlinear simulation. In：Technical Papers. Part 1（A88-3217612-39），29th Structures，Structural Dynamics and Materials Conference，Williamsburg，VA，United States，1988-4-18-20，Hampton，Virginia，United States：NASA Langley Research Center 1988：167～177

6 Waszak M R，Schmidt D K. Flight dynamics ofareoelastic vehicles. Journal of Aircraft，1988，25（6）：563～571

7 Li N X，Grant P R，Abbasi H. A comparison of the fixedaxes and the mean-axes modeling methods for flexible aircraft simulation. In：The 2010 AIAA modeling and simulation technologies conference（MSTC）Toronto，Ontario Canada. American Institute of Aeronautics and Astronautics，2010，1～25

8 Li Y W，Nahon M，Sharf I. Dynamics modeling and simulation of flexible airships. AIAA Journal，2009，47（3）：592 ～605

9 Huang X，Zeiler T. Dynamics of flexible launch vehicles with variable mass. In：44th AIAA Aerospace Sciences Meeting and Exhibit. Reno，Nevada，United States：American Institute of Aeronautics and Astronautics，2006：1～33

10 Nikravesh P E，Lin Y S. Use of principal axes as the floating reference frame for a moving deformable body. Multibody System Dynamics，2005，13（2）：211～231

11 Nikravesh P E，Lin Y S. Body reference frames in deformable multibody system. International Journal for Multiscale Computational Engineering，2003，1（2）：1～16

12 Nikravesh P E. Understanding mean-axes conditions as floating reference frames. Advances in Computational Multibody Systems. Computational Methods in Applied Sciences，2005，2：185～203

13 Shi P，Mcphee J，Heppler G R. A deformation field for Euler-Bernoulli beams with applications to flexible multibody dynamics. Multibody System Dynamics，2001，5（1）：79～104

14 洪嘉振，蒋丽忠.动力刚化与多体系统刚-柔耦合动力学.计算力学学报，1999，16（3）：295～301（Hong J Z，Jiang L Z. Dynamic stiffing and multibody dynamics with coupled rigid and deformation motions. Chinese Journal of Computational Mechanics，1999，16（3）：295～301（in Chinese））

15 洪嘉振，尤超蓝.刚柔耦合系统动力学研究进展.动力学与控制学报，2004，2（2）：1～6（Hong J Z，You C L. Advances in dynamics of rigid-flexible coupling system. Journal of Dynamics and Control，2004，2（2）：1～6 （in Chinese））

16 蒋丽忠，洪嘉振.作大范围运动弹性梁的动力刚化分析.计算力学学报，1998，15（4）：407～412（Jiang L Z，Hong J Z. Dynamics of an elastic beam in large overall motion. Chinese Journal of Computational Mechanics，1998，15（4）：407～412（in Chinese））

17 蒋丽忠，赵跃宇.作大范围运动柔性结构的耦合动力学.北京：科学出版社，2007（Jiang L Z，Zhao Y Y. The coupling dynamics of flexible structure in large overall motions. Beijing：Science Press，2007（in Chinese））

18 黎亮，章定国，洪嘉振.作大范围运动FGM矩形薄板的动力学特性研究.动力学与控制学报，2013，11 （4）：329～335（Li L，Zhang D G，Hong J Z. Dynamics of rectangular functionally graded thin plates undergoing large overall motion. Journal of Dynamics and Control，2013，11（4）：329～335（in Chinese））

19 吴胜宝，章定国.大范围运动刚体-柔性梁刚柔耦合动力学分析.振动工程学报，2011，24（1）：1～7（Wu S B，Zhang D G. Rigid-flexible coupling dynamic analysis of hub-flexible beam with large overall motion. Journal of Vibration Engineering，2011，24（1）：1～7（in Chinese））

20 刘锦阳，邹凡，余征跃.大变形刚-柔耦合系统仿真和实验研究.振动工程学报，2011，24（6）：646～651 （Liu J Y，Zou F，Yu Z Y. Simulation and experimental study for rigid-flexible couple dynamic system with large deformation. Journal of Vibration Engineering，2011，24 （6）：646～651（in Chinese））

Received 17 April 2014，revised 31 July 2014.

*The project supported by the National Nature Science Foundation of China（11432010，11072044）；The Research Fund for the Doctoral Program of Higher Education（20110041130001）；The Program for New Century Excellent Talents in University（NCET-11-0054）

A COMPARISON OF SEVERAL DYNAMIC MODELS FOR SLENDER FLEXIBLE SPACE STRUCTURE*

Zhao Guowei1Wu Zhigang1，2†
（1. State Key Laboratory of Structural Analysis for Industrial Equipment，Dalian University of Technology，Dalian 116024，China）（2. School of Aeronautics and Astronautics，Dalian University of Technology，Dalian 116024，China）

AbstractDynamic modeling method of on-orbit maneuvering of free-free slender flexible space structures was studied. In literature，a dynamic model without rigid-flexible coupling terms was adopted for designing motion controller. Establishing a dynamic model with relatively accuracy is the premise of obtaining a well-designed motion controller，therefore，it is necessary to establish the coupling model and find the difference between them. A floating reference frame was chosen as local reference frame，whose origin is consistent with the center of mass. The assumed mode method was used for discretizing the deformation parameter. The rigid-flexible coupling dynamic equations of structure undergoing large overall plane motion were obtained based on the virtual work principle. Through several simulation examples，the difference between uncoupling equations and coupling equations was discussed，and the results show that the uncoupling model is not accurate enough and simple zeroorder model is more accurate and effective. The analysis provides an important basis for the subsequent motion controller design and vibration attenuation.

Key wordsflexible space structure， on-orbit transportation， floating reference frame， rigid-flexible coupling， free-free boundary

DOI：10. 6052/1672-6553-2014-070

通讯作者†E-mail：wuzhg@ dlut. edu. cn

Corresponding author†E-mail：wuzhg@ dlut. edu. cn