含间隙齿轮传动系统的非线性动力学特性的研究*

张晨旭杨晓东 张伟

（北京工业大学，北京 100124）



含间隙齿轮传动系统的非线性动力学特性的研究*

张晨旭†杨晓东 张伟

（北京工业大学，北京 100124）

摘要含间隙齿轮传动系统存在着丰富的非线性动力学行为，建立了两自由度齿轮传动系统的动力学模型，首先利用数值方法分析了齿轮传动系统的分岔和混沌动力学行为，然后将非光滑的间隙函数用光滑函数拟合，通过对系统进行多尺度摄动分析和计算，得到间隙函数拟合后的齿轮传动系统的非线性动力学现象，并与无拟合非光滑系统的数值结果进行比较分析，为含间隙齿轮传动系统的研究奠定了基础.

关键词间隙， 非光滑， 分岔

2015-01-22收到第1稿，2015-02-16收到修改稿.

*国家自然科学基金资助项目（11322214，11290150，11290152）

引言

随着我国空间技术的迅速发展，空间飞行器日益大型化和柔性化，空间结构日趋庞大，空间可展机构在现代航天领域中得到广泛应用［1］.空间可展机构中绝大部分都可以视为由铰链作为连接器构成的，由于制造误差、折叠误差及磨损和材料变形等造成的铰链间隙，使结构在展开过程中运动副之间会出现接触和碰撞，导致空间可展机构具有非光滑力学特征，以致出现大型空间结构失稳、指向精度下降等问题，进而影响飞行器的姿态运动和展开精度［2 -4］.

齿轮运动副是可展机构中很重要的一种连接部件，机构锁定之后，齿轮副之间的间隙会使齿轮之间产生碰撞—分离—碰撞这种复杂的冲击现象，产生较大的冲击、振动和噪声，严重时会造成机构的损坏，因此，对含齿侧间隙的齿轮传动系统进行动力学分析有着十分重要的意义［5 -6］.对齿轮传动系统的间隙非线性问题已进行了大量的研究，分别建立了单自由度［7 -10］、三自由度［11］间隙非线性动力学模型，考虑周期时变刚度的影响，并用各种方法研究齿轮系统的周期运动、混沌响应及分岔［12］.但由于齿轮系统中的间隙分段函数产生的非光滑动力学特性的研究仍然是一个难点，本文将间隙分段函数拟合为光滑函数，对比了拟合后的齿轮传动系统与原非光滑系统的动力学行为，对含间隙齿轮传动系统的研究具有一定的促进作用.

1 力学模型及运动微分方程

图1为一含间隙的两自由度齿轮传动系统的力学模型，两个质量M的质块分别由刚度K1、K3的线性弹簧和阻尼连接于支撑，两质块之间通过K2和C2连接，两质块分别受简谐激振力Pj（t）= Pjcosωt，j =1，2.取间隙的中点作为坐标原点，水平向右为正方向，建立坐标系，当右边质块的位移差等于B或- B时，将会与刚度为K4的弹簧接触（即齿轮开始啮合），经过一定时间改变速度方向后，以新的初值运动，啮合分开，然后再与刚度K4的弹簧接触，如此反复.

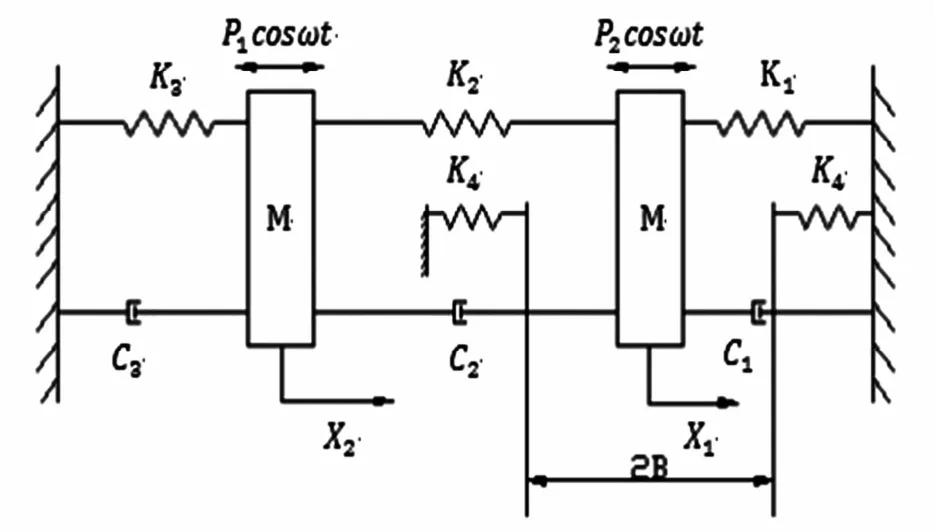
图1 两自由度齿轮传动系统的模型Fig. 1 Model of Two-degrees-of-freedom gear transmission system

图1所示齿轮传动系统的运动微分方程为

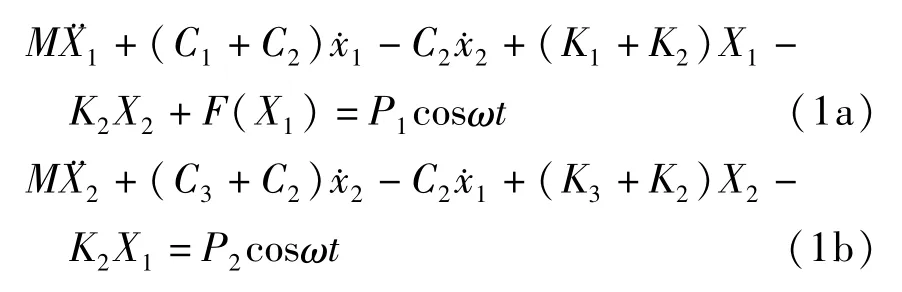
式中

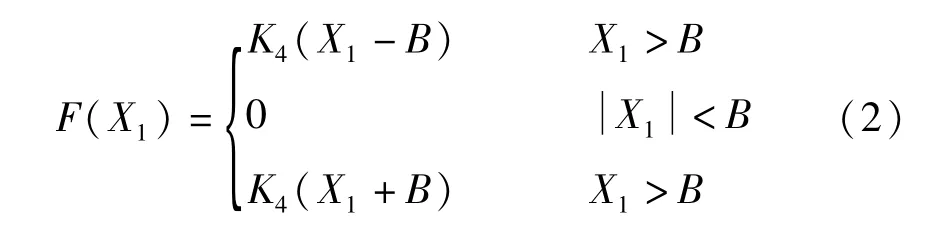
2 含间隙齿轮传动系统的数值研究

对原方程（1）无量纲化进行数值模拟，取无量纲量

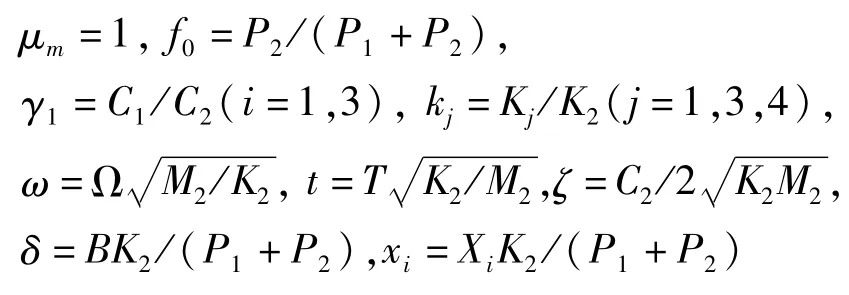
则方程（1）化为无量纲方程

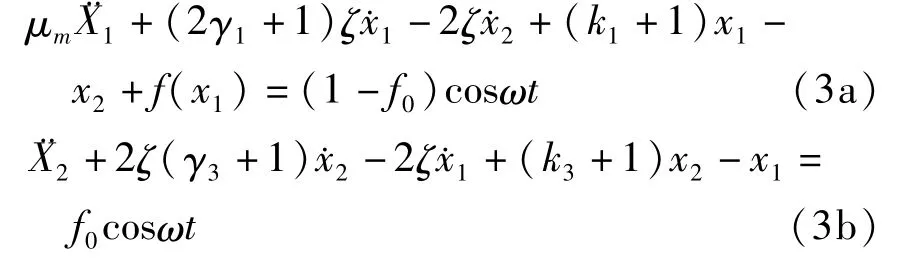
式中

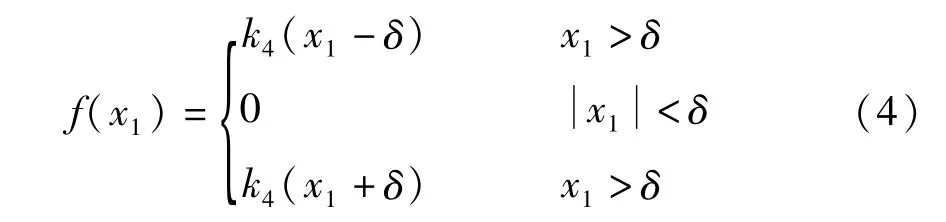
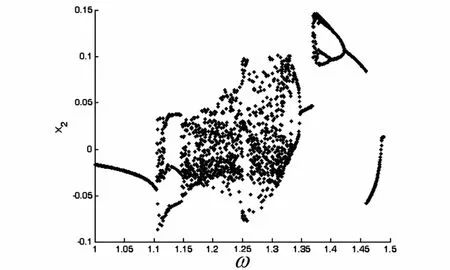
图2 系统的全局分岔图Fig. 2 The global bifurcation diagram of the system

取初始参数μm= 1，ζ= 0. 02，γ1= 2，γ3= 2，k1=5，k3=5，k4= 30，f0= 0. 5，δ= 0. 02，固定这些参数，改变外激励频率，研究齿轮传动系统的非线性动力学行为.由数值仿真得到图2所示的分岔图（图中：横坐标为激励频率；纵坐标为右边质块运动到弹性约束处的速度），揭示了齿轮传动系统的全局动力学特性：外激励频率在一定范围内变化时，非线性系统的动态特性呈现出周期运动与混沌运动交替出现的运动规律.

可见，当参数ω变化时，齿轮传动系统存在丰富的非线性动力学行为，为了更详细地描述系统的分岔行为，对系统进行相图响应分析，如图3所示.

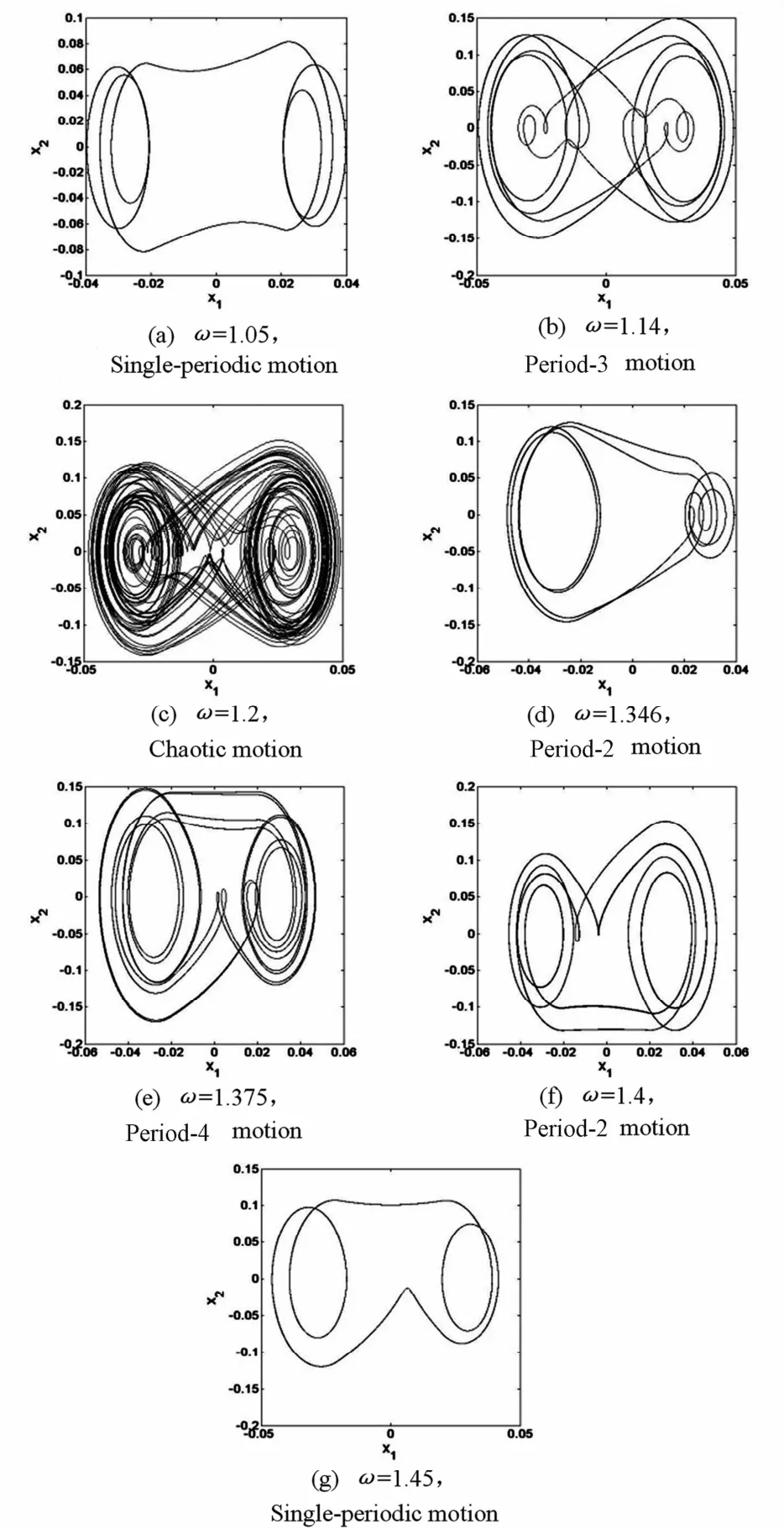
图3 相图Fig. 3 Phase diagram

3 拟合间隙函数的齿轮传动系统的分析

式（2）中，令x1= X1/ B，则方程（1a）中的间隙函数F（X1）变为如下形式

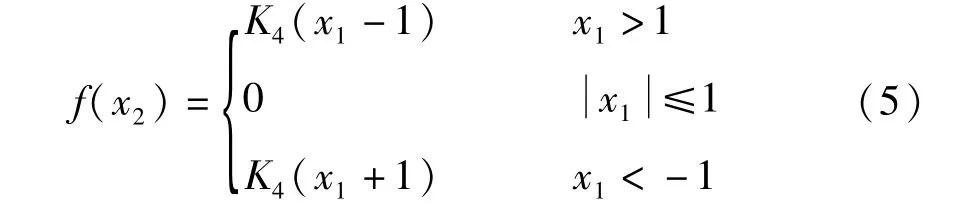
为了能够求得系统的解析解，利用高次多项式拟合分段间隙函数，拟合多项式的次数越高曲线越精确，不同拟合次数的多项式与原间隙函数的对比如图4所示.间隙函数可以写成如下近似表达式

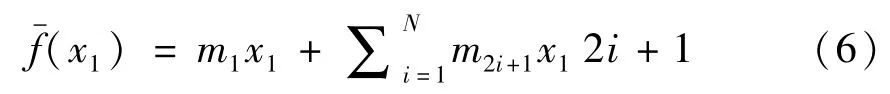
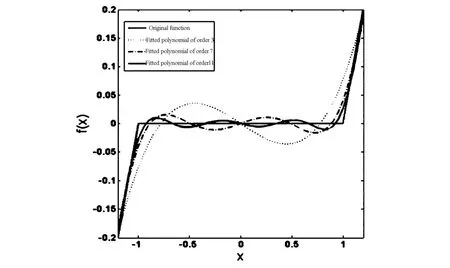
图4 分段间隙函数的拟合多项式与原函数的对比Fig. 4 Comparison of the fitted polynomial and the original piecewise function

将（6）式代入（1）式，取i =1，方程（1）化为

为了简化对式（7）的分析，需要对上述两式解耦，并将系统原有坐标变换成主坐标.首先要求系统的振型矩阵，方程（7）的自由振动微分方程为

Ω为系统的固有频率.

利用上式的特征方程求得系统的固有频率Ω1、Ω2，代入（9）得系统的振型矩阵

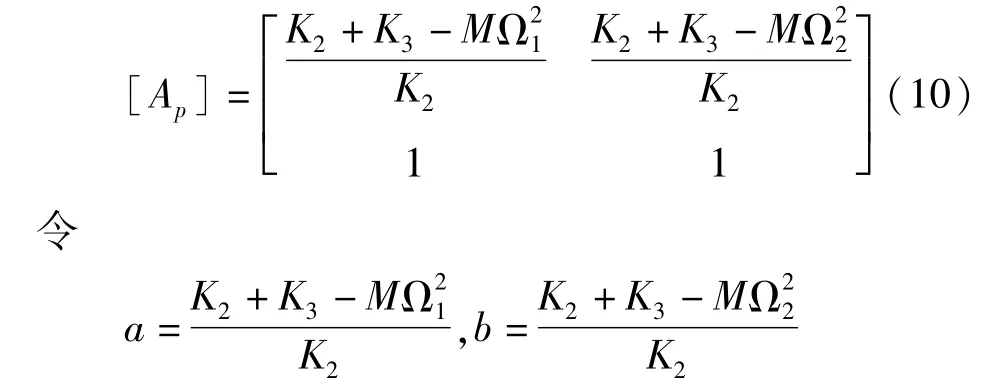
下面进行坐标变换，将方程（7）改写为

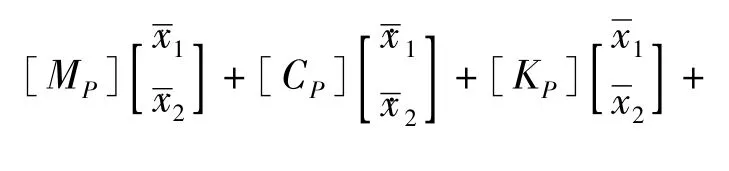
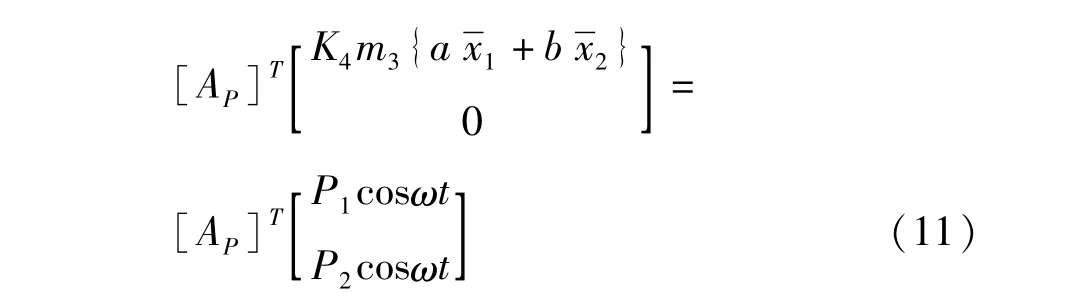
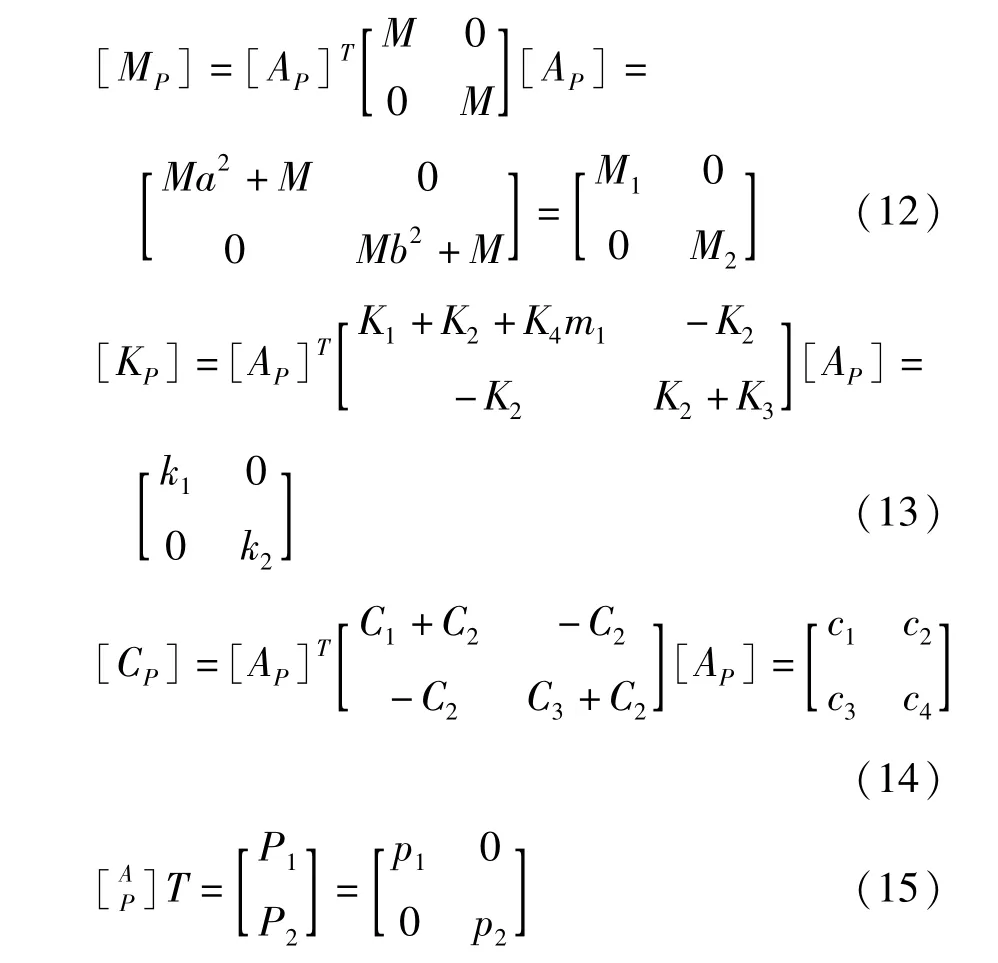
其中［AP］T为振型矩阵［AP］的转置矩阵.

将式（11）展开，省去x上面的横线，并分别除以M1、M2得

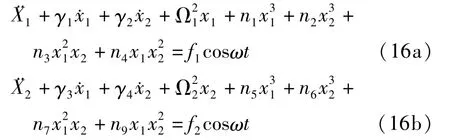
其中

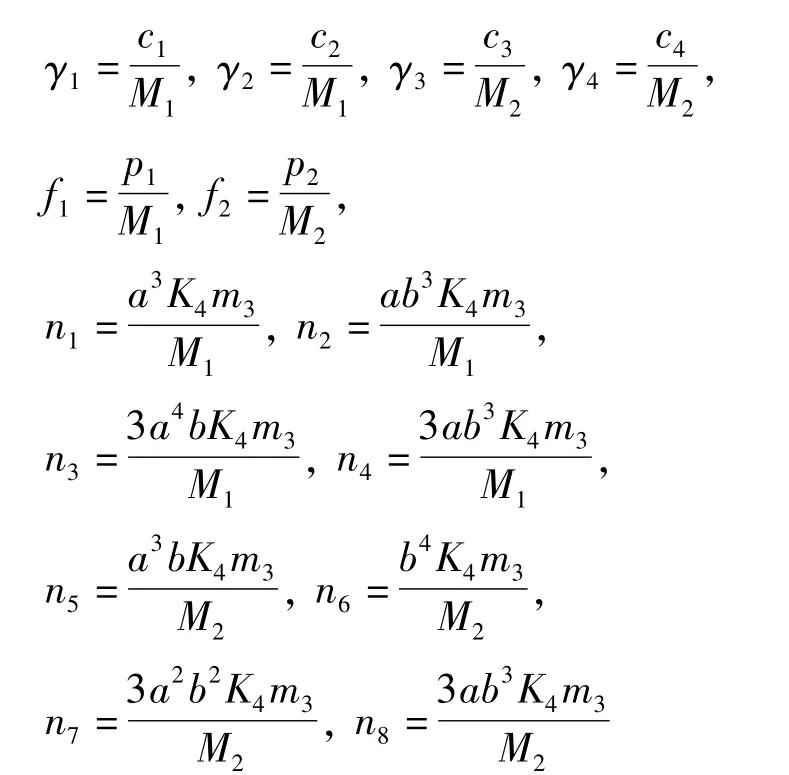
对方程（16）进行多尺度摄动分析，选取共振关系为

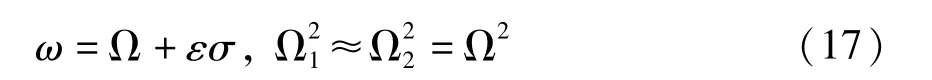
σ为系统的调谐参数.引入小参数将式（18）代入式（16）得

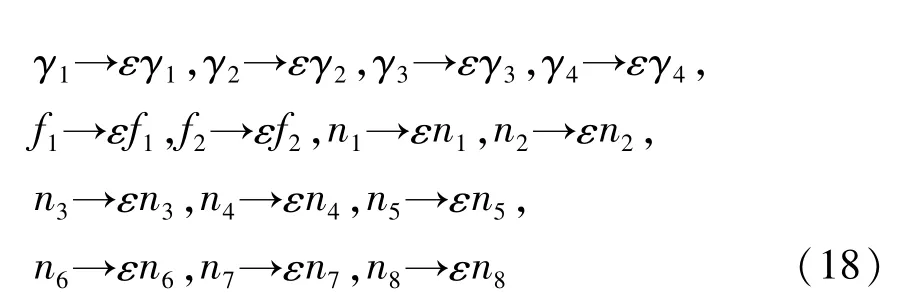
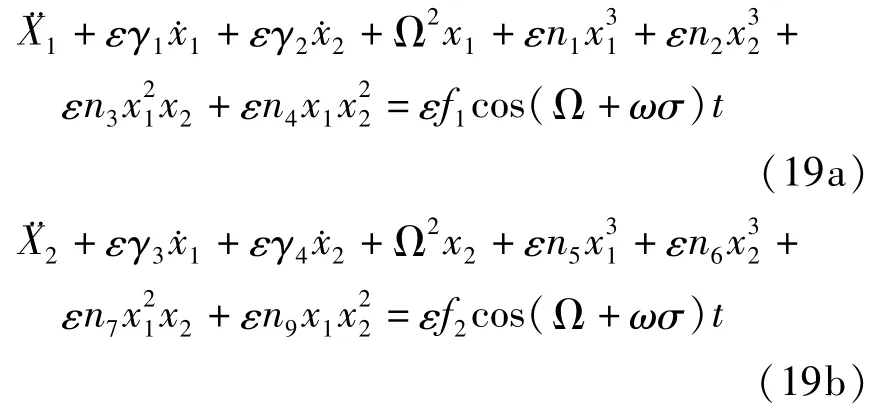
设方程的一致渐近解为

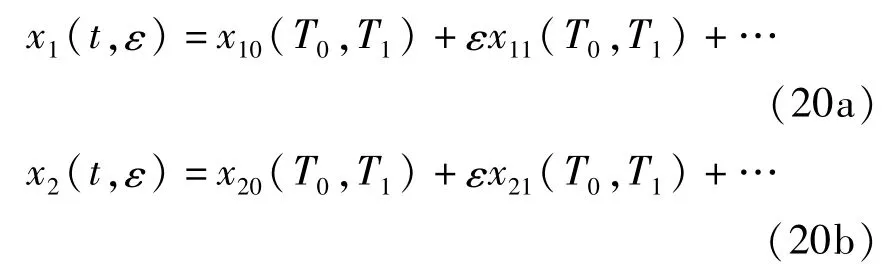
式中T0= t，T1=εt.

定义下列算子

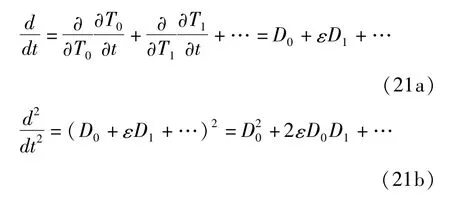
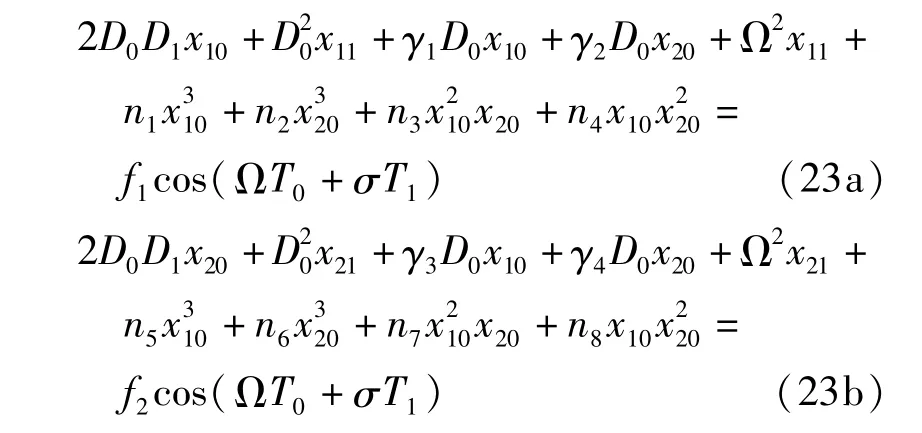
设0阶方程组的解为

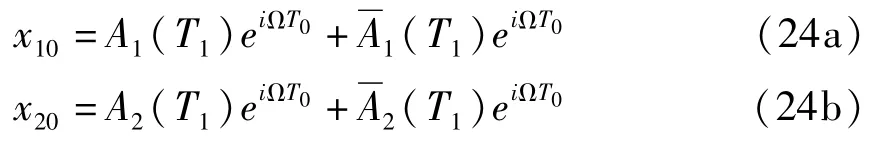
式中A表示A的复共轭项.

将通解（24）代入方程（23）得

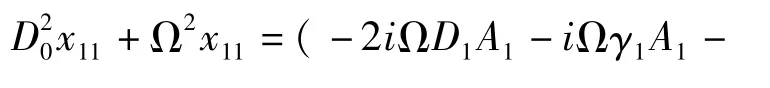
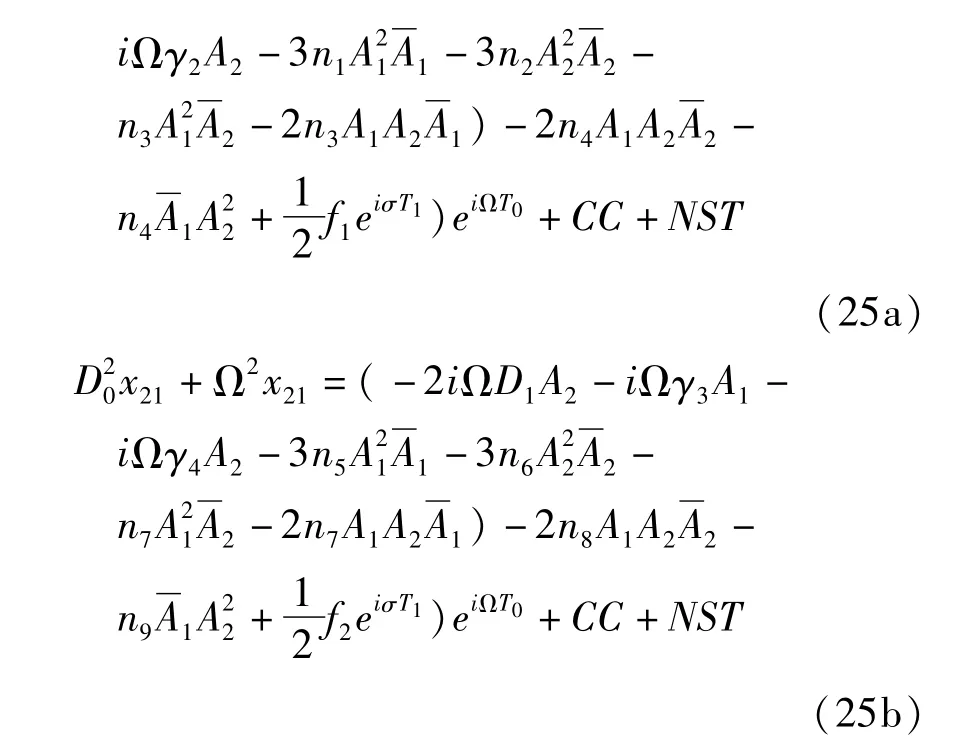
其中CC、NST表示方程的共轭项和长期项.

消除方程（25）的长期项，令系数等于零，得到下列复数形式的平均方程

函数Ai和Ai表示为如下形式

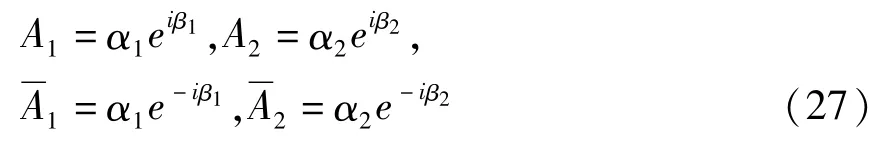
将方程（27）代入方程（26），分离实部虚部，得到极坐标形式的平均方程如下

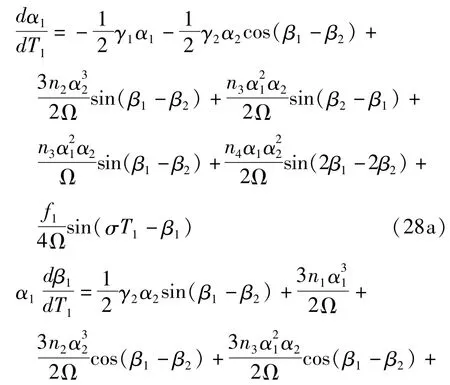
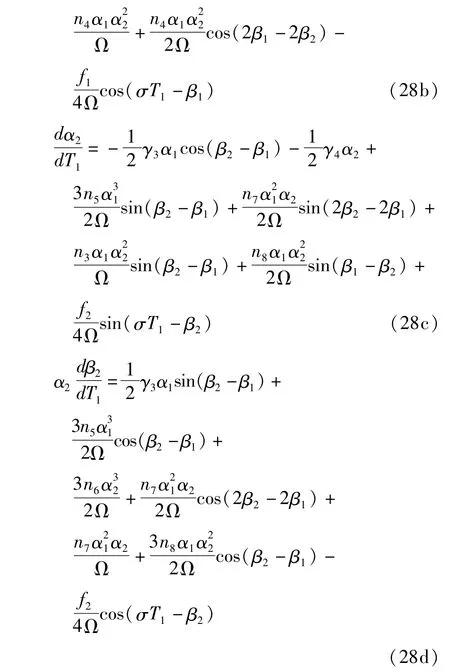
令φ1=σT1-β1，φ2=σT1-β2，考虑稳态响应，即

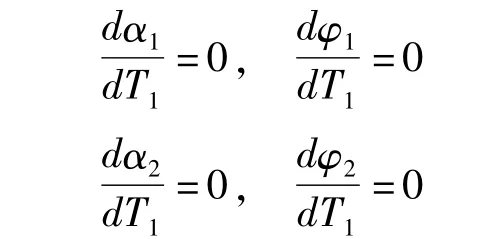
得到幅频响应方程

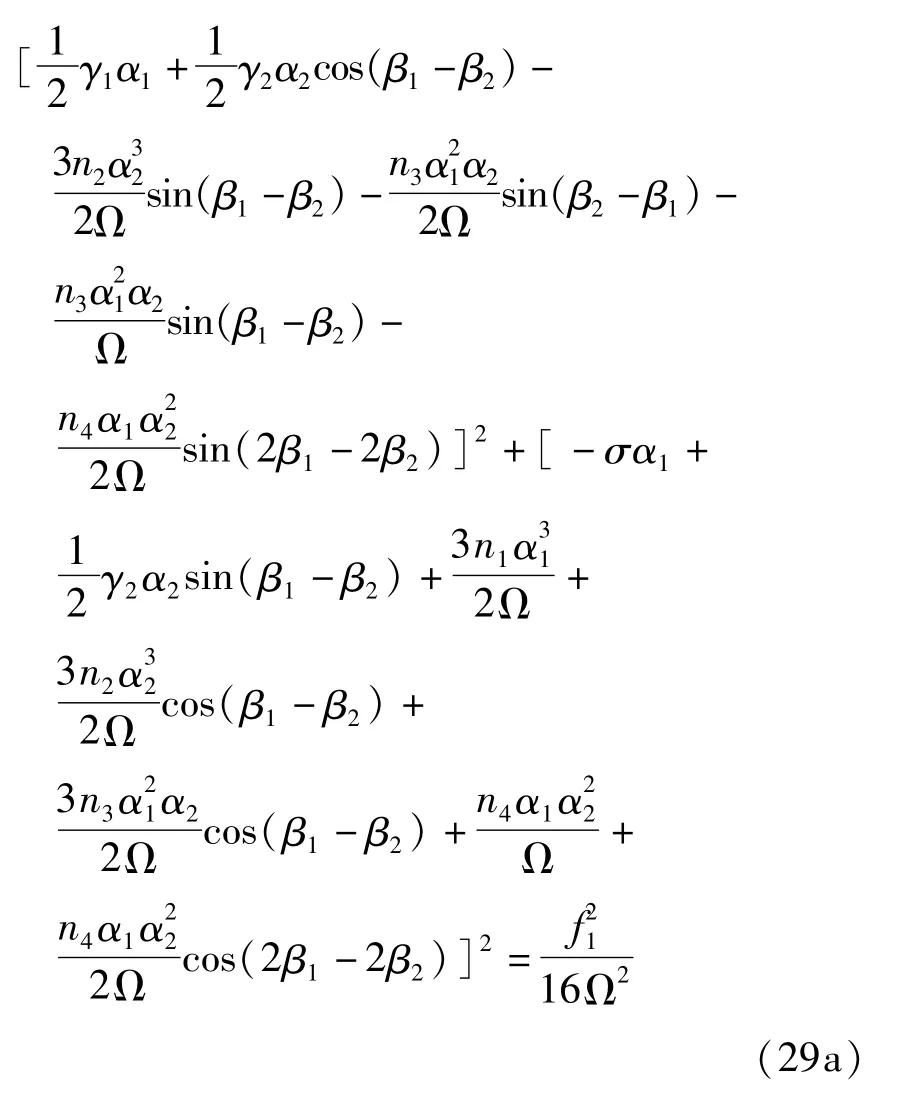
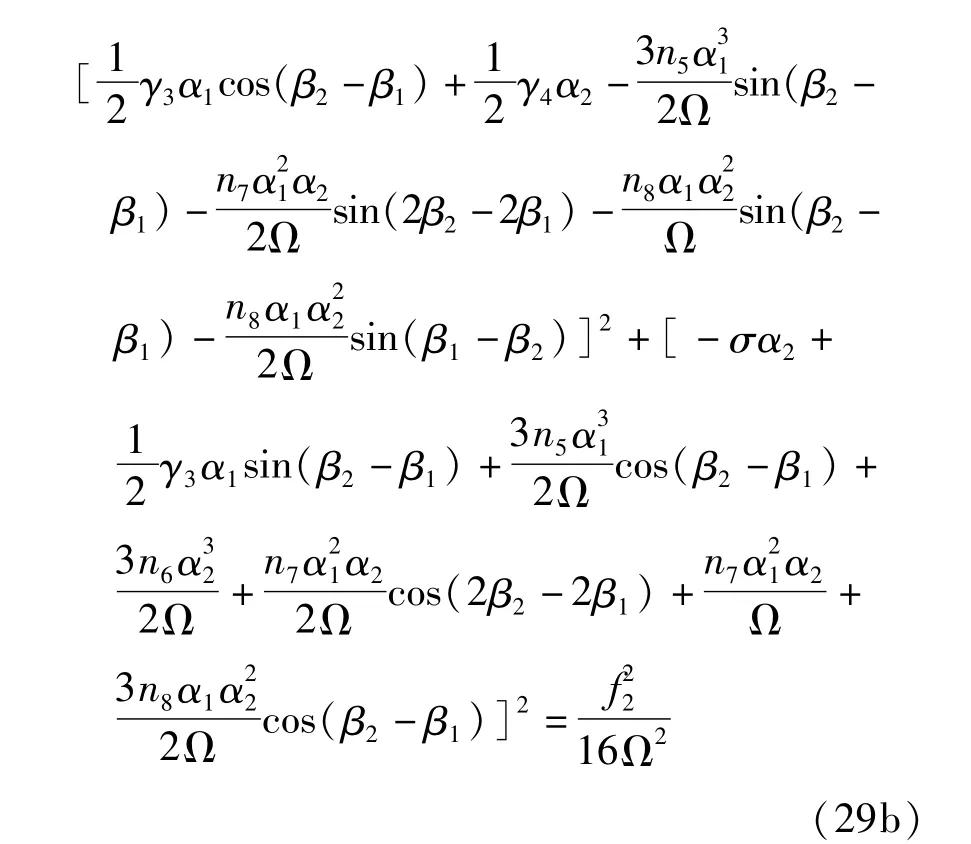
4 数值结果对比

将原方程的数值结果与拟合后的数值结果进行对比，考察将间隙分段函数拟合后方程的近似解析解能够在多大程度上反映原方程的非线性动力学特性.

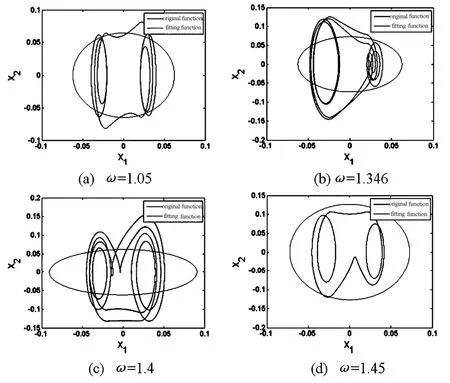
图5 相图响应曲线对比图Fig. 5 Comparison of phase diagram

将拟合后得到的平均方程进行数值模拟，与原方程的相图响应曲线进行比较，如图5所示，可以看到，当系统为单倍周期时，拟合后的结果与原方程的结果相差较小，但当系统运动的周期数增加时，拟合后的结果与原方程相差较大.图6为两种不同频率下原方程的幅频响应曲线与拟合后方程的幅频响应曲线的对比，图中蓝色的“·”表示直接由方程（1）得到的数值解，红色的“·”表示由平均方程（29）得到的结果，可以看到两种方法得到的幅频响应曲线同样呈现硬弹簧特性，两种结果相差不大.表示这种将间隙函数拟合后用多尺度进行解析研究的方法，只能用于近似研究运动情况相对简单的系统，而对于运动情况复杂的系统还需要用其他方法进行研究.

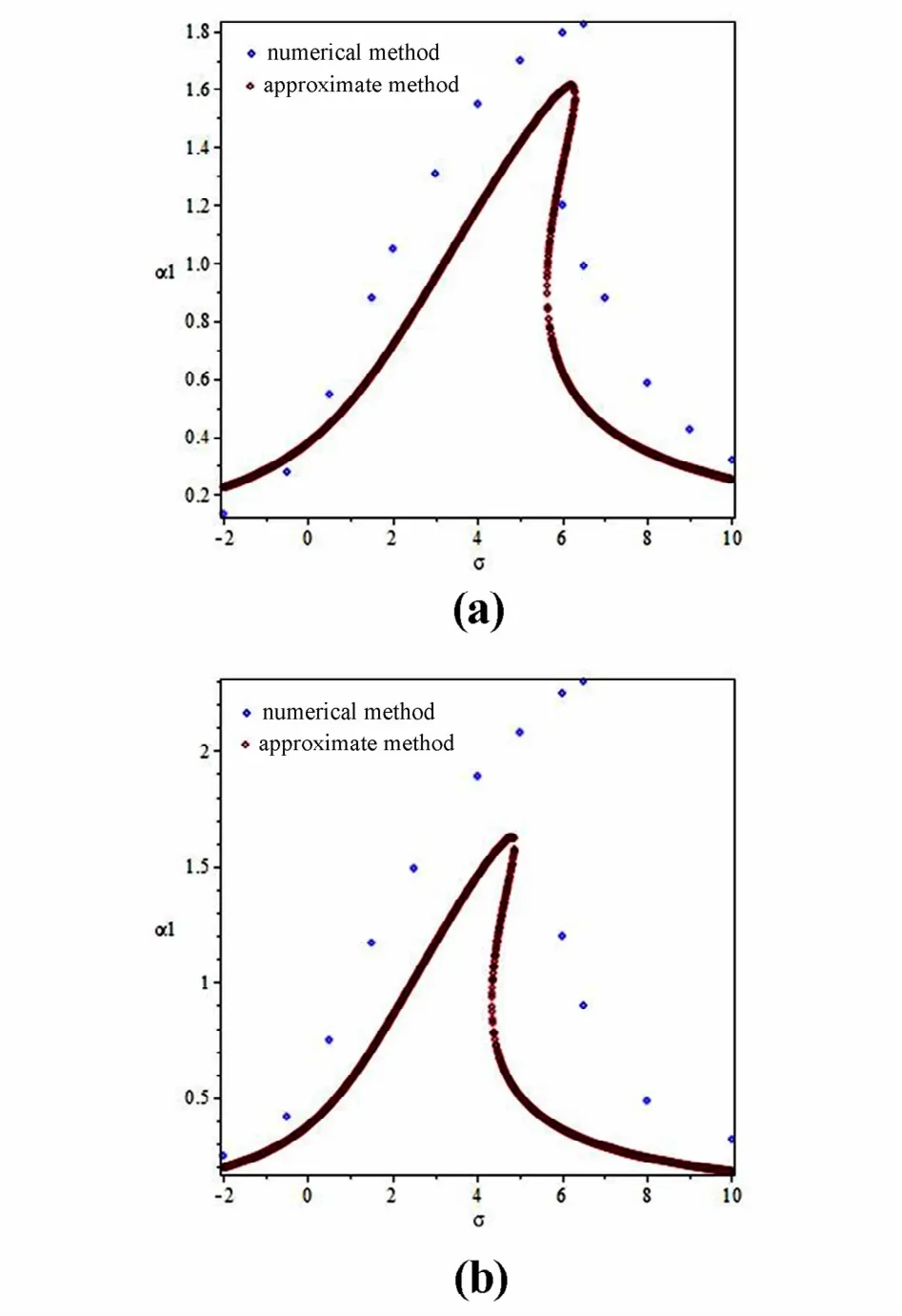
图6 不同频率对应的幅频响应曲线Fig. 6 Frequency response diagrams

5 结 论

1）含间隙的齿轮传动系统，由于受到外部扰动的影响，系统中将会出现周期运动、混沌运动等现象.随着外激励频率的变化，系统依次经历单倍周期运动，混沌运动，多倍周期运动，又回到二倍周期运动，最后系统再次进入单倍周期运动.

2）通过分析含间隙齿轮传动系统出现的几种形式的非线性现象，对于选择合适的系统参数，减小甚至是消除振动对系统的损耗有一定的参考意义.

3）将分段间隙函数拟合后，分别在平均方程和原方程的基础上作出了幅频响应曲线和相图响应曲线，对比表明，将分段间隙函数拟合是研究较简单非光滑系统的有效工具，这种方法给出了一种用解析方法近似研究非光滑动力学系统的途径，对非光滑系统的进一步研究奠定了基础.

参 考 文 献

1 Li X Z，Zheng F B. Dynamic response of solar deployment on spacecraft system considering joint clearance. ActaAstronautica，2012，81（1）：174～185

2 Nurre G S，Sharkey J P，Nelson J D. Bradley. Preserving mission，on-orbit modificationsto Hubble space telescope pointing control system. Journal of Guidance Control and Dynamics，1995，18（2）：222～229

3 马兴瑞，王本利，苟兴宇.航天器动力学-若干进展及应用.北京：科学出版社，2001（Ma X R，Wang B L，Gou X Y. Spacecraft dynamics-development and application. Beijing：Science press，2001（in Chinese））

4 曹登庆，初世明，李郑发等.空间可展机构非光滑力学模型和动力学研究.力学学报，2013，45（1）：3～15（Cao D Q，Chu S M，Li Z F. The nonsmooth mechanics model and dynamics research of spatial developable mechanism. Acta Mechanica Sinica，2013，45（1）：3～15（in Chinese））

5 李万祥，牛卫中.一类含间隙系统的分岔与混沌的形成过程.振动与冲击，2005，24（3）：47～49（Li W X，Niu W Z. Bifurcation and chaos of a system with a pair of symmetric set up elastic stops. Journal of Vibration and Shock，2005，24（3）：47～49（in Chinese））

6 马永靖，丁旺才，杨小刚.碰撞振动系统的参数自调节混沌控制.振动与冲击，2007，26（1）：24～26（Ma Y J，Ding W C，Yang X G. Chaos control of a vibro-impact system with parameter adjustment. Journal of Vibration and Shock，2007，26（1）：24～26（in Chinese））

7 Kahraman A，Singh R. Non-linear dynamics of a spur gear pair. Journal of Sound and Vibration，1990，142（1）：49～75

8 Blankenship G W，Kahraman A. Steady state forcedresponse of a mechanical oscillator with combined parametric excitation and clearance type non-linearity. Journal of Sound and Vibration，1995，185（5）：743～765

9 Raghothama A，Narayanan S. Bifurcation and chaos in geared rotor bearing system by incremental harmonic balance method. Journal of Sound and Vibration，1999，226 （3）：469～492

10 王三民，沈允文，董海军.含摩擦和间隙直齿轮副的混沌与分叉研究.机械工程学报，2002，38（9）：8～11 （Wang S M，Shen Y W，Dong H J. Chaos and bifurcation analysis of a spur gear pair with combined friction and clearance. Chinese Journal of Mechanical Engineering，2002，38（9）：8～11（in Chinese））

11 刘晓宁.三自由度齿轮传动系统的非线性振动及混沌控制.西安：西北工业大学，2003（Liu X Y. Nonlinear oscillations and chaos control for three-degree-of-freedom gear transmission system. Xi′an：Northwestern Polytechnical University，2003（in Chinese））

12 郜志英，沈允文，董海军等.齿轮系统倍周期分岔和混沌层次结构的研究.机械工程学报，2005，41（4）：44～48（Gao Z Y，Shen Y W，et al. Research on period-doubling bifurcation and chaos hierarchy in gear system. Chinese Journal of Mechanical Engineering，2005，41（4）：44 ～48（in Chinese））

Received 22 January 2015，revised 16 February 2015.

*The project supported by the National Natural Science Foundation of China（11322214，11290150，11290152）

STUDY ON NON-LINEAR DYNAMICS OF GEAR TRANSMISSION SYSTEM WITH CLEARANCE*

Zhang Chenxu†Yang Xiaodong Zhang Wei
（Beijing University of Technology，Beijing 100124，China）

AbstractAs the gear transmission system with clearance responses in a way of abundant nonlinear dynamics，this paper establishes a dynamic model of two-degree-of-freedom gear transmission system. Firstly，the bifurcation of the gear transmission system and the chaotic dynamic behavior using the numerical method is investigated，and the nonsmooth function is then fitted with the smooth function. Moreover，nonlinear dynamic phenomenon of gear transmission system with fitted clearance function is achieved using multi-scale perturbation. Eventually，the results are compared with that of nonsmooth system without numerical fitting，which also provides essential data for the future research of gear transmission system with a clearance.

Key wordsclearance， nonsmooth， bifurcation

DOI：10. 6052/1672-6553-2015-042

通讯作者†E-mail：zhangchenxu0218@126. com

Corresponding author†E-mail：zhangchenxu0218@126. com