环型桁架卫星天线的非线性动力学分析*

侯飞张伟

（1.山西大同大学煤炭工程学院，大同 037009）（2.北京工业大学机电学院机械结构非线性振动与强度北京市重点实验室，北京 100124）



环型桁架卫星天线的非线性动力学分析*

侯飞1，2张伟2†

（1.山西大同大学煤炭工程学院，大同 037009）（2.北京工业大学机电学院机械结构非线性振动与强度北京市重点实验室，北京 100124）

摘要我国航天工业迫切需要掌握可入轨后展开的大型网架式空间结构技术，而环形桁架可展天线具有应用空间大、结构形式简明的特点，是目前大型卫星天线较为理想的结构形式［1 -3］.本文基于Zhang et al建立的环形天线模型为研究对象并在此基础上建立了天线振动时的非线性常微分运动方程，运用matlab数值模拟方法研究了热激励对系统非线性动力学行为的影响.

关键词环型桁架， 非线性动力学， 混沌运动

2015-07-06收到第1稿，2015-11-14收到修改稿.

*国家自然基金资助项目（11290152，11272016），山西大同大学校青年科学研究项目（20080827）

引言

随着航天技术的迅速发展，大型卫星天线结构研究越来越受到人们的重视.可展开结构最大的特点就是具有可展开性：在发射时处于收拢状态，在发射入轨接受到指令后开始展开，完成展开后锁定并且保持工作状态.但在一定范围内天线的口径增大，质量并没有成比例的增加，且并不会改变结构形式，是目前大型卫星天线较为理想的结构形式［4 -6］.

图1 环形桁架可展开天线结构Fig. 1 Circular mesh antenna

环形桁架可展开天线结构（图1）由四部分组成：前索网、金属反射网、拉索、可展开环形桁架、后索网.其中可展开环形桁架是由n个结构完全相同的平行四边形单元组成，这些单元通过由固定夹角的铰链相连接成为一个封闭的多边形环结构.前后索网周边固定在环型桁架上，通过中层竖向拉索相互联系，在索网中施加预拉力后，使前索网形成所需的抛物面，金属发射网附着于前索网完成电波反射任务.其展开原理利用了平行四边形对角可伸缩的特点，由连续的驱动索穿过周边环型桁架可伸缩的对角杆单元（套筒机构），通过电机带动驱动索，从而使结构展开.

本文对环形桁架在热场条件下的非线性动力学行为进行数值研究，为环形桁架可展开天线的实践提供重要的依据，同时对大型空间可展开天线问题的研究积累技术手段.

1 环型桁架卫星天线的动力学方程

本文把环形桁架可展天线等效成图2所示的圆柱壳结构［7 -10］.等效后壳体的中面半径为R，轴向的长度为L，圆柱壳沿径向方向的厚度为h.在壳体中面建立曲线坐标（如图2所示），壳内任一点的位移为u、v、w，分别代表x，θ，z三个方向，并假设圆柱壳处于变化的温度场中.

假设等效圆柱壳中面的位移分量分别为u0，v0，w0，根据Reddy一阶剪切变形壳理论［11 -13］采用von Karman的大变形几何关系，并根据Hamilton原理，考虑自由-自由以及固定-固定的边界条件，最终得到系统由横向位移表示的无量纲非线性常微分方程如下

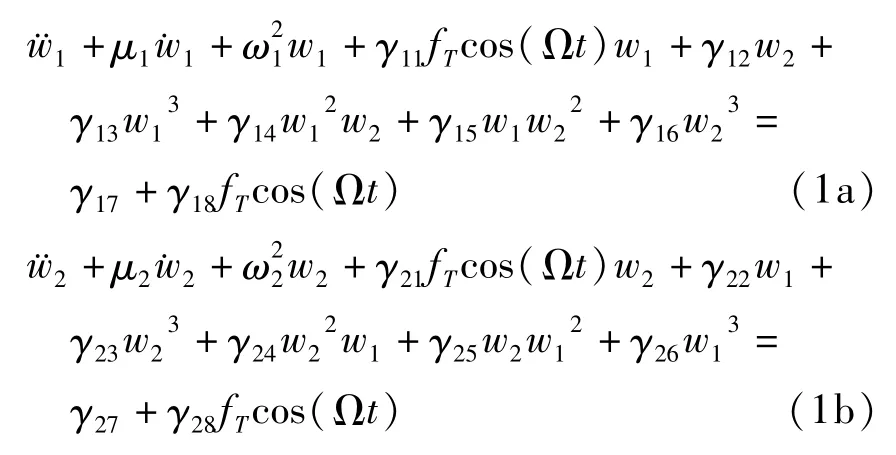
方程（1）的系数表达式详见文献［9 -11］.

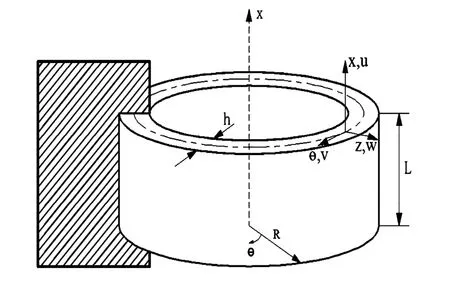
图2 等效圆柱壳的力学模型Fig. 2 The model of equivalent circular cylindrical shell

2 数值分析

本文以热激励作为控制参数对系统的非线性振动特性进行研究，选取的初始条件和参数值分别为

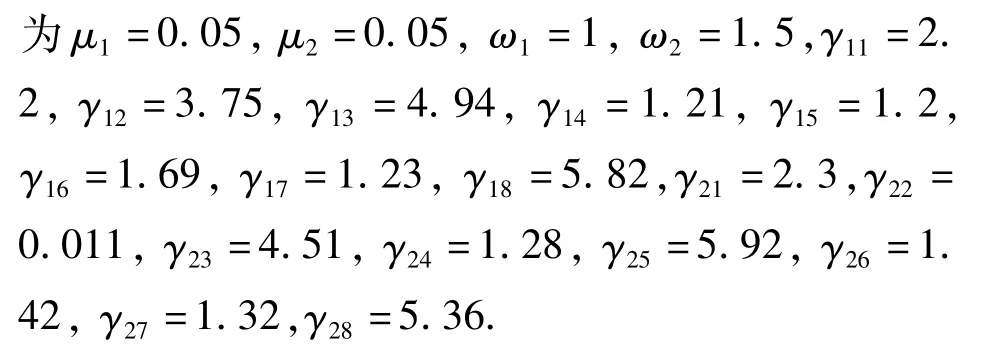
通过固定初始参数，只改变热激励fT的大小，研究热激励fT的变化对等效圆柱壳的动力学行为的影响.图3是系统在受到热激励fT=5～15时的分叉图.

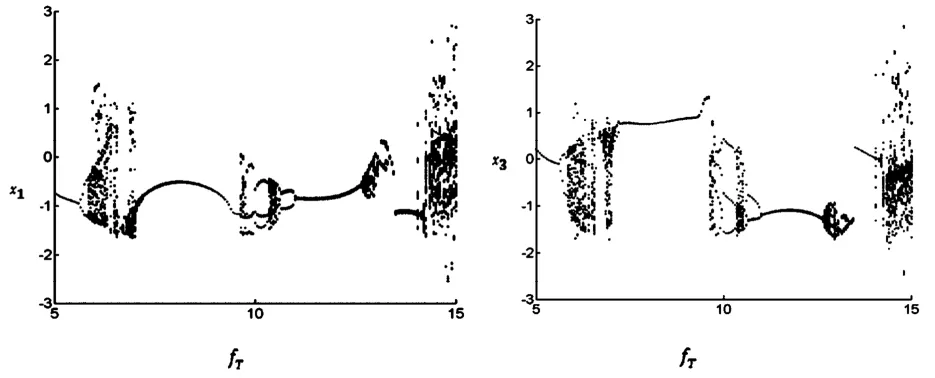
图3 系统随热激励fT变化的分叉图Fig. 3 The bifurcation diagram of x1and x3with the thermal excitation fTfor the system

由图3可以看出，在热激励幅值fT=5～5. 625的区域中，系统出现周期运动，随着热激励幅值的增大系统变为二倍周期运动，随后进入混沌运动.伴随着激励的增大，系统再次出现周期运动，在激励幅值fT=10. 01时系统慢慢进入三倍周期运动，随后出现二倍周期和四倍周期运动，最后又进入混沌运动.其中x1=ω1，x3=ω2.

根据热激励分叉图3，分析环型桁架卫星天线在等效成圆柱壳时非线性动力学特性.由于时变热载荷会导致天线结构和卫星姿态发生明显的振动和响应，在下面的研究中，我们选取特定的热激励幅值.通过对应情况下的二维相图、三维相图、波形图分析系统动力学特性如非线性振动形式和振幅大小等.

下面给出的图示中，图（a）为平面（x1，x2）上的二维相图；图（b）为平面（x3，x4）上的二维相图；图（c）为一阶模态（t，x1）振动特性的波形图；图（d）为二阶模态（t，x3）振动特性的波形图；图（e）～（f）为空间（x1，x2，x3）上的三维相图.其中x2=˙ω1，x4=˙ω2.

通过分叉图3可以发现当热激励幅值fT=5. 5时，系统的振动形式为规律的周期运动，其相图、三维相图，波形图如图4所示.

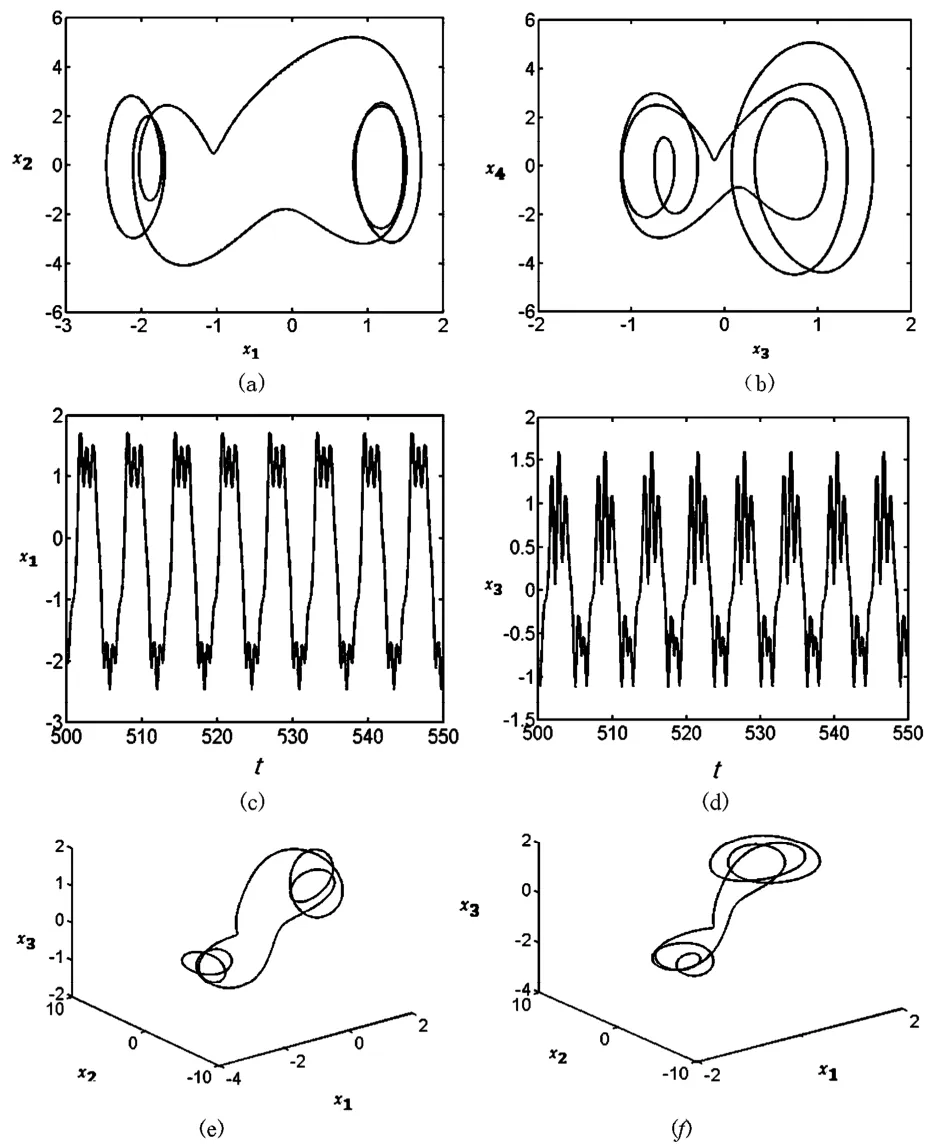
图4 fT=5. 5时系统的周期运动Fig. 4 The periodic motion of the system when fT=5. 5

增大热激励幅值，当fT= 5. 625时系统振动形式出现二倍周期运动，其平面相图、三维相图、波形图如图5所示.

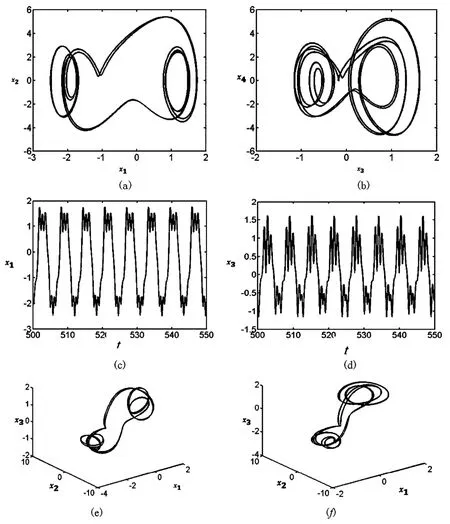
图5 fT=5. 625时系统的二倍周期运动Fig. 5 The period-2 motion of the system when fT=5. 625

随着热激励幅值的增大，系统在fT=6. 2附近进入混沌运动，图6给出了此时系统运动的平面相图、三维相图、波形图和频谱图.

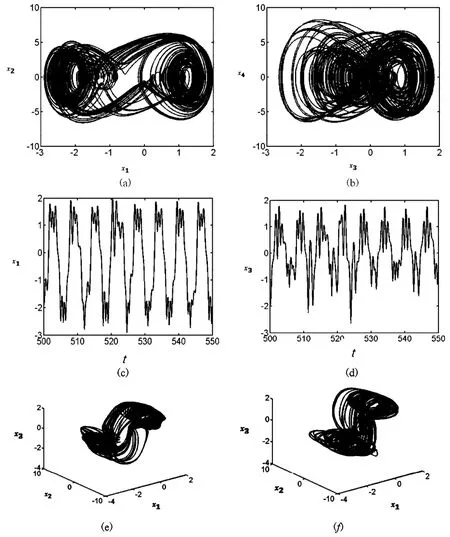
图6 fT=6. 2时系统的混沌运动Fig. 6 The chaotic motion of the system when fT=6. 2

随热激励幅值的增大，系统在fT= 10. 01附近进入三倍周期运动，图7给出了此时系统运动的平面相图、三维相图、波形图和频谱图.

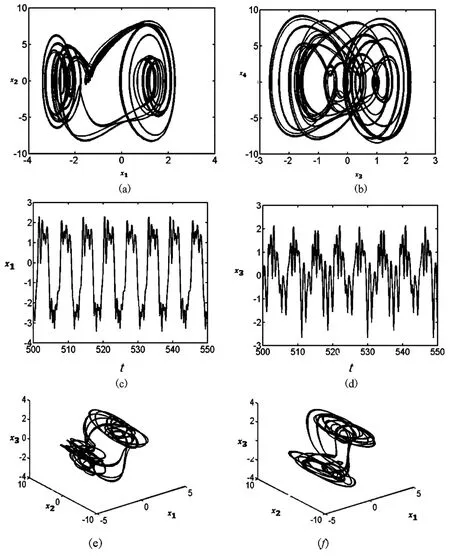
图7 fT=10. 01时系统的三倍周期运动Fig. 7 The period-3 motion of the system when fT=10. 01

进一步增大热激的励幅值，系统在fT= 10. 7附近进入二倍周期运动，图8给出了此时系统运动的平面相图、三维相图、波形图和频谱图.

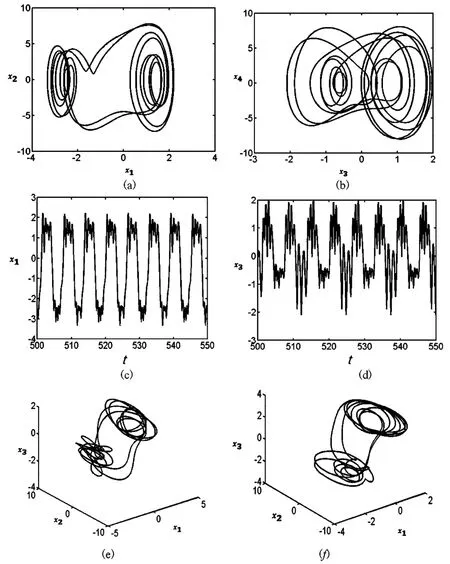
图8 fT=10. 7时系统的二倍周期运动Fig. 8 The two period-2 motion of the system when fT=10. 7

随着热激励幅值的增大，系统在fT= 13附近进入四倍周期运动，图9给出了此时系统运动的平面相图、三维相图、波形图和频谱图.

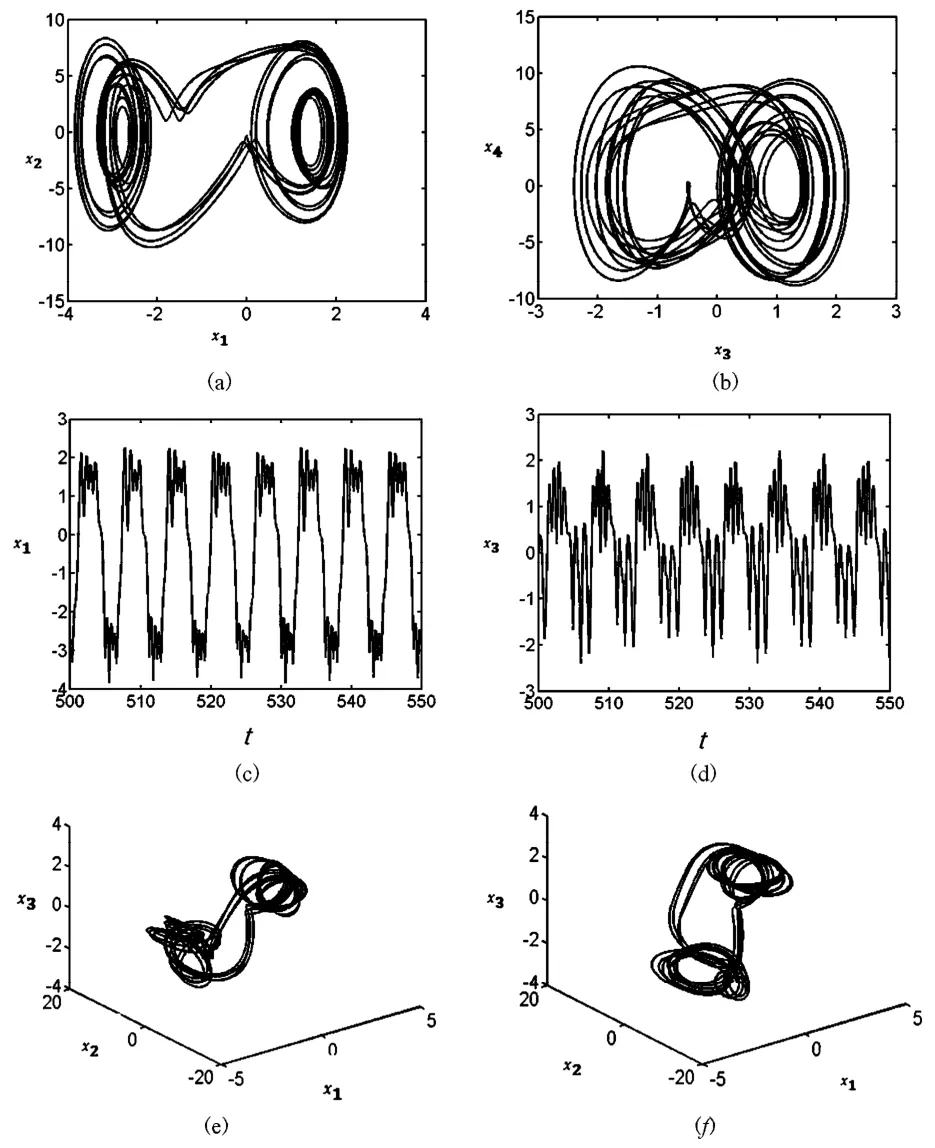
图9 fT=13时系统的四倍周期运动Fig. 9 The period-4 motion of the system when fT=13

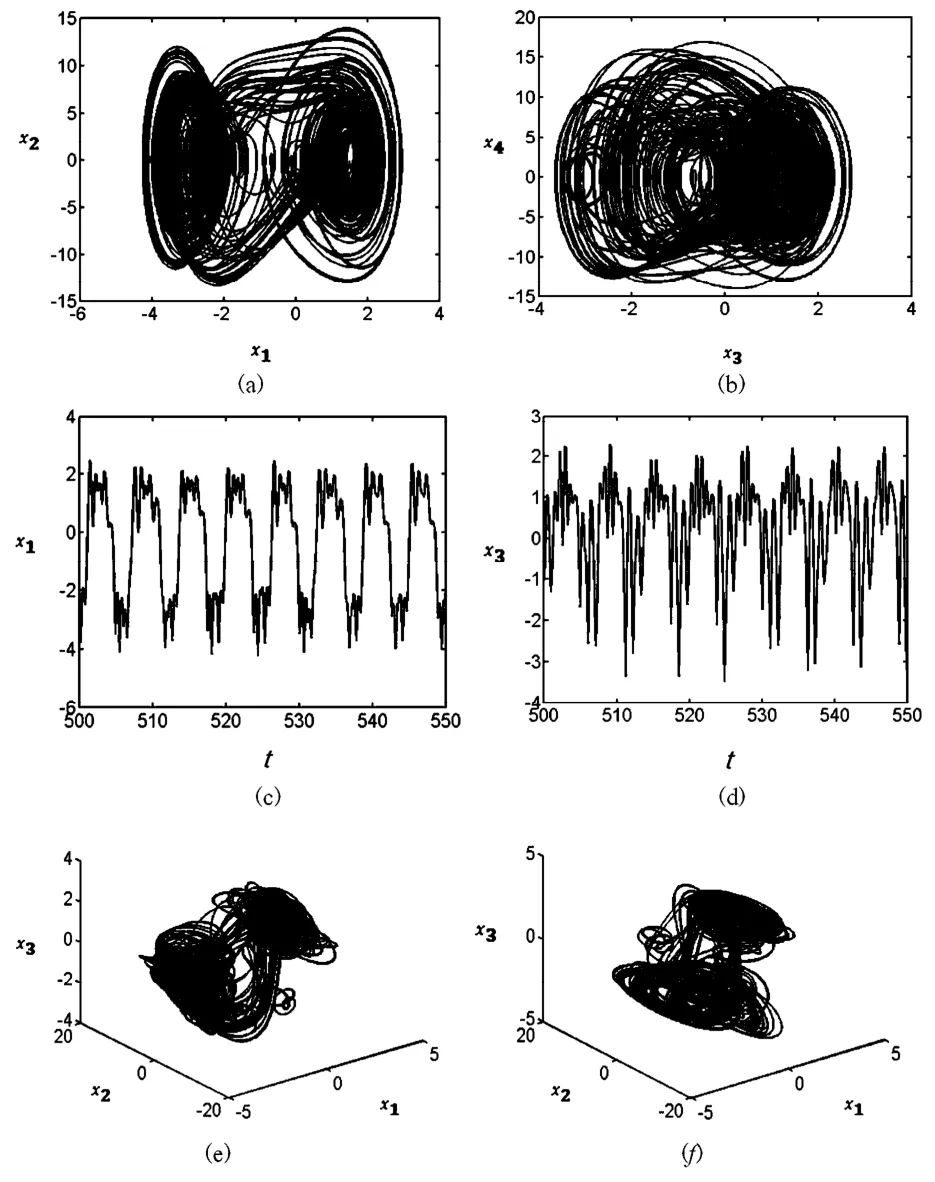
图10 fT=14. 25时系统的混沌运动Fig. 10 The chaotic motion of the system when fT=14. 25

经过一段时间后，热激励的幅值继续增大，系统在fT=14. 25附近再次进入混沌运动，图10给出了此时系统运动的平面相图、三维相图、波形图和频谱图.

4 结论

本文研究环型桁架卫星天线非线性动力学问题，分析了热激励对系统的非线性动力学行为的影响.系统的非线性振动现象如图4～图10所示，我们可以发现系统经历了从周期运动变为混沌运动，结果表明环型桁架卫星天线在受到热激励作用下存在周期运动、多倍周期运动以及混沌运动等多种复杂动力学行为.当系统从周期运动变化到混沌运动时，系统的第一阶模态和第二阶模态的振幅都随着热激励幅值fT的改变而发生较剧烈的改变.由此可知，热激励幅值fT的改变对此系统的非线性振动特性具有重要的影响，时变热载荷会导致天线结构和卫星姿态发生明显的振动响应，天线结构的振动响应主要集中在第一、二阶固有模态上.

参 考 文 献

1 胡海岩，田强，张伟，金栋平，胡更开，宋燕平.大型网架式可展开空间结构的非线性动力学与控制.力学进展，2013，43（4）：390～414（Hu H Y，Tian Q，Zhang W，et al. Nonlinear dynamics and control of large deployable space structures composed of trusses and meshes. Advances in Mechanics，2013，43（4）：390～414（in Chinese））

2 赵孟良，关富玲.考虑摩擦的周边桁架式可展天线展开动力学分析.空间科学学报，2006，26（3）：220～226 （Zhao M L，Guan F L. Deployment dynamic analysis of circular truss deployable antenna with fiction. Chinese Journal of Space Science，2006，26（3）：220～226（in Chinese））

3 闵桂荣，郭舜.航天器热控制.北京：科学出版社，1998 （Min G R，Guo S. The thermal control of spacecraft. Beijing：Science Press，1998（in Chinese））

4 杨玉龙，关富玲，张淑杰.可展桁架天线温度场和热变形分析.空间科学学报，2005，25（3）：235～240（Yang Y L，Guan F L，Zhang S J. Thermal-structural analysis of deployable truss antenna. Chinese Journal of Space Science，2005，25（3）：235～240（in Chinese））

5 朱敏波，曹峰云，刘明治等.星载大型可展开天线太空辐射热变形计算.西安电子科技大学学报（自然科学版），2004，25（1）：28～31（Zhu M B，Cao F Y，Liu M Z，et al. The calculation of thermal radiaiton distortion for large deployable antennas in satellites. Journal of Xidian University，2004，25（1）：28～31（in Chinese））

6 安翔，冯刚，张铎.大型空间析架结构热分析的有限元方法.强度与环境，2000，（2）：18～23（An X，Feng G，Zhang D. Finite-element model for the thermal analysis of large main truss of space station′ssolar-array. Structure & Environment Engineering，2000，（2）：18～23（in Chinese））

7 Hao Y X，Zhang W，Yang J，Wang J H. Dynamic response of cantilever FGM cylindrical shell. Applied Mechanics and Materials，2011，130-134：3986～3993

8 Hao Y X，Zhang W，Yang J. Nonlinear dynamics of cantilever FGM cylindrical shell under 1：2 internal resonance relations. Mechanics of Advanced Materials and Structures 2012，20（10）：819～833

9 Zhang W，Hao Y X，Yang J. Nonlinear dynamics of FGM circular cylindrical shell with clamped-clamped edges. Composite Structures，2012，94（3）：1075～1086

10 Zhang W，Zhou R，Zu J W. Nonlinear vibrations of a shell-shaped workpiece during high-speed milling process. Nonlinear Dynamics，2013，72（4）：1～21

11 Reddy J N，Chandrashekhara K. Geometrically non-linear transient analysis of laminated，doubly curved shells. International Journal of Non-Linear Mechanics，1985，20 （2）：79～90

12 Reddy J N，Liu C F. A higher-order shear deformation theory of laminated elastic shells. International Journal of Engineering Science，1985，23（3）：319～330

13 Reddy J N，Arciniega R A. Shear deformation plate and shell theories：from Stavsky to present. Mechanics of Advanced Materials and Structures，2004，11（11）：535～582

Received 06 July 2015，revised 14 November 2015.

*The project supported by Major Program of National Natural Science Foundation of China（11290152，11272016）and the School Program of Shanxi Datong University（20080827）

ANALYSIS ON NONLINEAR DYNAMICS OF CIRCULAR ANTENNA*

Hou Fei1，2Zhang Wei2†
（1. College of Coal Engineering，Shanxi Datong University，Datong 037009，China）（2. Beijing Key Laboratory of Nonlinear Vibrations and Strength of Mechanical Structures，College of Mechanical Engineering，Beijing University of Technology，Beijing 100124，China）

AbstractThe increasing demand for advanced and large-aperture space antennas has promoted the remarkable development of the aerospace industry. The circular Antennas could be as small as possible during transportation，while it should be as large as needed for effective operation when the antenna is fully deployed on the orbit. Based on the earlier results，a equivalent circular cylindrical shell model is proposed to represent the circular continuum antenna，and the nonlinear governing equations of motion are derived for the equivalent circular cylindrical shell system under thermal excitation. By means of numerical simulations in MATLAB programme，the influence of thermal excitation on the dynamical behaviors for the nonlinear system is investigated.

Key wordscircular antenna， nonlinear dynamics， chaotic motion

DOI：10. 6052/1672-6553-2016-014

通讯作者†E-mail：hfybsy2000@163. com

Corresponding author†E-mail：hfybsy2000@163. com