生条中纤维左头端的分布
张弘强, 胡远波, 姜 展, 匡雪琴, 郁崇文,3
(1. 东华大学 纺织学院, 上海 201620; 2. 上海工程技术大学 基础教学学院, 上海 201620;3. 东华大学 纺织面料技术教育部重点实验室, 上海 201620)
生条中纤维左头端的分布
张弘强1, 胡远波2, 姜 展1, 匡雪琴1, 郁崇文1,3
(1. 东华大学 纺织学院, 上海 201620; 2. 上海工程技术大学 基础教学学院, 上海 201620;3. 东华大学 纺织面料技术教育部重点实验室, 上海 201620)
为进一步探究纱条中纤维的分布规律,模拟纱条中纤维的排列情况,对纤维左头端沿纱条轴向服从均匀分布的假设进行实验验证。通过示踪纤维的方法测定若干给定长度的生条片段中染色纤维的左头端数,并利用χ2拟合检验法对所测数据进行检验。结果表明:生条中纤维左头端沿生条轴向服从均匀分布的假设是合理的;通过改变染色纤维的几何特征、种类及所取生条的片段长度考察了对纤维左头端数的影响,证明了所取生条的片段长度对纤维左头端沿生条轴向服从均匀分布的结论没有显著影响,最终为预测纱条的性能提供了基础。
纱条; 纤维排列; 左头端数; 均匀分布
成纱性能由纤维性能及其在纱条中的排列所决定,因此,对纤维在纱条中随机排列的描述是研究成纱性能的关键。所谓排列是每根纤维沿纱条轴向所呈的分布,通常认为是随机的,而均匀分布是随机分布的一种。为方便研究,前人建立了关于纱条中纤维排列的假设。Martindale[1]提出了理想纱条的概念,即指纤维在纱条中随机地排列,即各纤维相互独立且在纱条中各处出现的机会完全均等,且在纱条不匀理论的研究中假设每根纤维长度、线密度均相同,纤维伸直、头尾相接且与纱轴平行排列等条件。随后,Suh[2]和Zeidman[2]关于纱条不匀理论的研究均以类似的假设为基础。Rao[4]给出了理想纱条严格的数学定义,其中提到在纱条上任何长的区间内恰好出现一个纤维左或右头端的概率仅与区间的长度有关,而与区间所在位置无关。严广松等[5]在Rao所给出理想纱条定义的基础上,考虑纤维的长度分布,将定义变为在纱条上任何长为s的区间上,含有N个纤维的头端,s为纤维的最长长度,这些头端在长为s的任何区间内是均匀分布。Brown等[6]提出了纤维的头端在纱条长度方向上是一个“平稳的点过程”。严广松等[7]指出纤维随机排列的特征可以使用纤维头端在纱长度方向上的分布来表示,提出了一种广义均匀分布来描述纤维头端的分布情况,并在已知纱中纤维长度和纱条不匀率的条件下,得到了这种广义均匀分布的参数估计。Jiang等[8]、严广松等[9]通过假设纤维左头端沿纱条轴向服从均匀分布,建立起对纤维在纱条中随机排列的模拟以及对成纱不匀的分析。
综上所述,均假设纤维左头端沿纱条轴向服从均匀分布,即假设若干等长纱条片段内纤维左头端数无明显差异,但是研究中没有表明纤维左头端分布的实际情况。本文用实验的方法探究纤维左头端在纱条中的实际分布情况,以期为以后模拟更接近实际的纤维状态(纤维不等长度、线密度,不同的弯钩类型、弯钩大小等)在纱条中的排列提供参考。
1 实验部分
为探究纤维左头端在生条中的实际分布,需对一定长度生条片段内的纤维左头端数进行检测。因生条中的纤维数量庞大,为方便计数,将一定量染色纤维混入生条,以代表生条片段中纤维的情况。
一般认为,生条中纤维的形态大致可分为对折、打圈、卷曲、倾斜和弯钩,其中呈弯钩形态的纤维占主要部分[10]。本文定义的纤维左、右头端即为纤维的左、右边界点,纤维的左、右边界点是指在纤维上沿纱条轴向方向的最左、右一点所在的位置。弯钩纤维的左、右头端分别如图1中A、B所示。
图2示出纤维左头端的计数原则,其依据纤维左头端与生条片段边界线(竖直虚线表示)的位置关系。图中的4根纤维,分别标记为1、2、3、4。计算纤维的左头端数以生条段的左边界线为准,即包含恰好达到左边界的纤维左头端,如图2中纤维1计入生条段1;2、3计入生条段2;4计入生条段3。
1.1 实验原料
为探究纤维的不同特性对纤维左头端分布的影响,对几种不同特性的纤维进行染色,染色纤维的特性如表1所示(棉纤维-2取自棉卷,即棉卷中的纤维性能同棉纤维-2)。

表1 染色纤维的参数指标Tab.1 Parameters of colored fiber
1.2 实验条件及方案
本文实验所用为同一种棉卷,其定量为100 g/30 mm(纵向)×40 mm(横向)。
实验方法:将约为1 g的染色纤维随机分布在梳棉机的喂入棉层上,制得含有染色纤维的生条。连续量取一定长度的生条对其中的染色纤维进行计数。先对表面及浅层的染色纤维进行计数,操作中基本不触碰生条;再将生条轻轻拨开,对生条内部的染色纤维进行计数。实验过程应尽量小心操作,切勿使之发生变形与伸长。
2 实验结果与讨论
2.1 实验结果
表2示出所取生条的片段长度为1 cm时,连续截取20个片段中染色纤维左头端数的测试结果,以分析纤维特性与种类对生条中纤维左头端数分布的影响。

表2 1 cm的生条片段中不同染色纤维的左头端数Tab.2 Number of left ends of different kinds of color fibers in 1 cm segment of carded sliver
表3示出将一定长度的生条分别截取若干不同长度的生条片段,观察其中棉纤维-2左头端数的测试结果,以分析所取生条片段长度对纤维左头端数分布的影响。
2.2 实验分析与讨论
2.2.1 纤维左头端数的实际分布情况
用χ2拟合检验法对表2、3数据进行分析。χ2拟合检验法是当总体的分布未知时,根据来自总体的样本,检验关于总体分布假设的一种方法,方法中先假设总体所服从的分布,进而引入K.Pearson统计量[8-10],借此来反映样本的经验分布和所假设的理论分布之间的吻合程度,以此判断是否要接受原假设。本文实验中,假设H0为染色纤维左头端数沿生条轴向服从均匀分布,χ2计算值通过χ2拟合检验法的法则可得,χ2临界值根据显著性水平α=0.01通过查表可得。分析结果分别如表4、5所示。通过表4可知棉纤维-2的χ2计算值小于χ2临界值,接受原假设,表明纤维左头端数沿生条轴向服从均匀分布的假设是合理的。
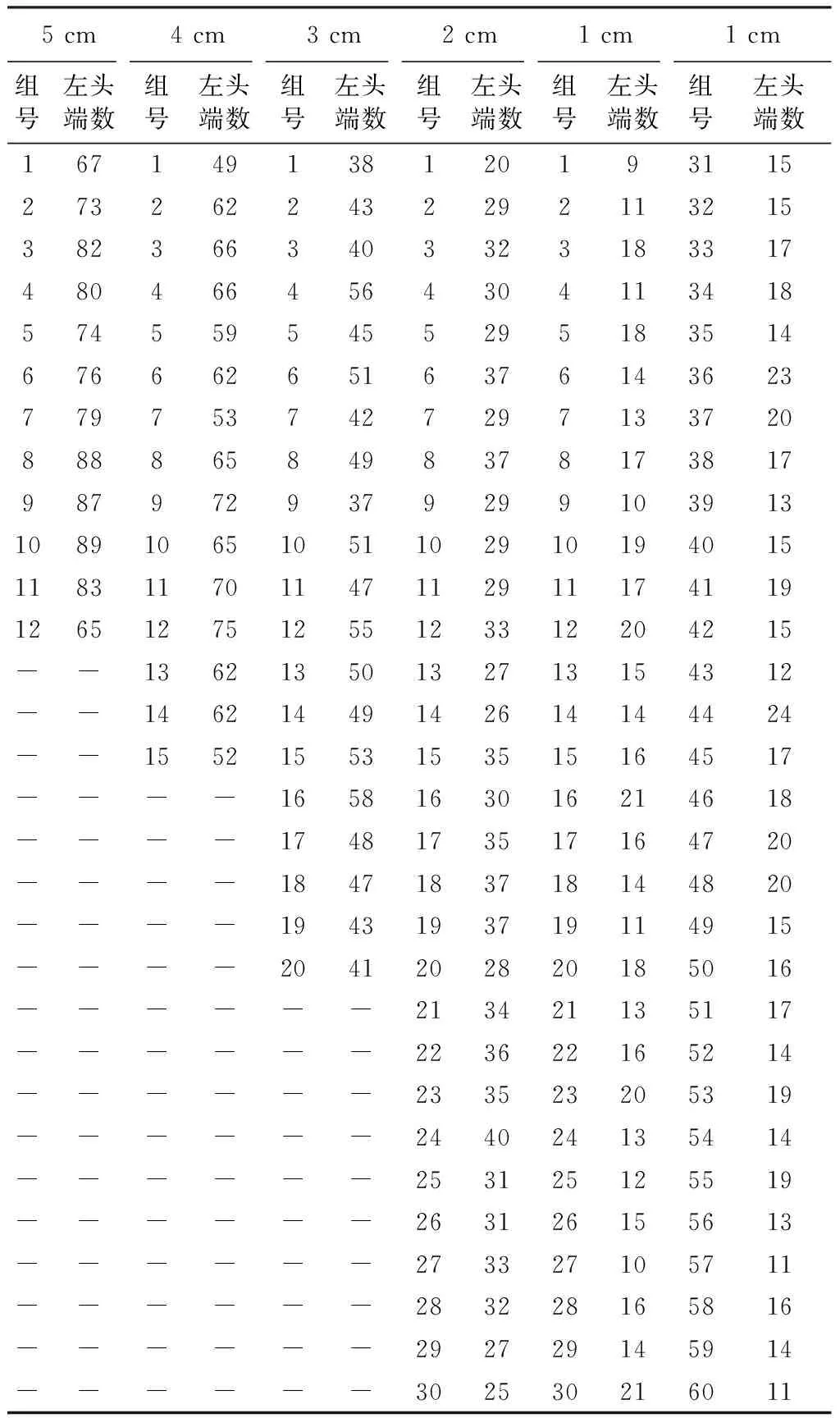
表3 不同片段长度的生条中棉纤维-2的左头端数Tab.3 Number of left ends of cotton fiber-2 carded sliver segments of different lengths

表4 生条中不同染色纤维左头端数分析表Tab.4 Analysis of number of left ends of different kinds of color fibers
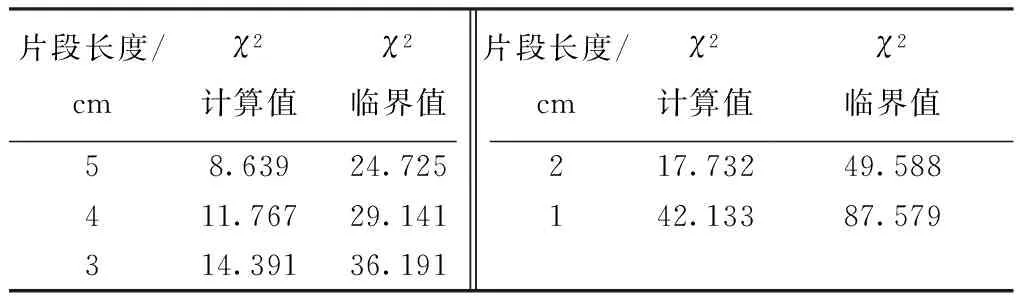
表5 不同片段长度的生条中棉纤维-2左头端数分析表Tab.5 Analysis of number of left ends cotton fiber-2 carded sliver segments of different lengths
2.2.2 纤维几何特征对纤维左头端数分布的影响
比较表4中棉纤维-1、棉纤维-2、棉纤维-3对应的χ2计算值与χ2临界值的关系可知,3种情况下χ2计算值均小于χ2临界值,说明各染色纤维左头端数沿生条轴向均服从均匀分布的假设是合理的,即棉纤维的长度与线密度对其左头端数分布情况无显著影响。
2.2.3 纤维种类对纤维左头端数分布的影响
比较表4中棉纤维、粘胶纤维、腈纶对应的χ2计算值与χ2临界值的关系可知,3种情况下χ2计算值均小于χ2临界值,说明各染色纤维左头端数沿生条轴向均服从均匀分布的假设是合理的,即纤维种类对其左头端数分布情况无显著影响。
2.2.4 生条片段长度对纤维左头端数分布的影响
由表5可知,当所取生条片段长度分别为5、4、3、2、1 cm时,χ2计算值均小于χ2临界值,说明染色纤维左头端数沿生条轴向服从均匀分布的假设是合理的,即所取生条片段长度对其左头端数分布情况无显著影响。
3 结 论
1)用χ2拟合检验法对所取生条片段中染色纤维的左头端数进行分析,结果表明可以接受纤维左头端数沿生条轴向服从均匀分布的结论,证明了前人研究中假设的合理性。
2)纤维的长度、线密度、纤维的种类均对生条中纤维左头端数的分布没有显著的影响。不同长度、线密度、种类的纤维在生条中,左头端数均呈均匀分布。
3)生条的片段长度对纤维头端数的分布没有显著影响,不同片段长度的生条中纤维左头端数沿生条轴向仍服从均匀分布。
为了更好地预测纱条的性能(如纱条不匀、强度等),在模拟纤维在纱条中随机排列时,可以继续假设纤维左头端为均匀分布,并考虑纤维的实际形态(纤维的长度、线密度、弯钩类型、弯钩比例),使模拟的纱条的性能更接近纱条的实际性能。
[1] MARTINDALE J G. A new method of measuring the irregularity of yarns with some observations on the origin of irregularities in worsted slivers and yarns[J]. J Textile Inst, 1943,36(2):35-47.
[2] SUH M W. Probabilistic assessment of irregularity in random fiber array-effect of fiberlength distribution on "variance-length curve"[J]. Textile Res J, 1976,45(2): 291-298.
[3] ZEIDMAN M I. A new perspective on yarn uneven-ness: components and determinants of general unevenness [J]. Textile Res J, 1990,60(3):1-6.
[4] RAO S J. The mathematical model for the ideal sliver and its applications to the theory of roller drafting[J]. J Textile Inst, 1961(52):570-600.
[5] 严广松, 苏玉恒. 理想纱条的纤维排列与随机过程分析[J]. 河南工程学院学报(自然科学版), 2014,26(1):1-5. YAN Guangsong, SU Yuheng. The alignment of fibers in ideal sliver and its analysis by stochastic process[J]. Journal of Henan Institute of Engineering(Natural Science Edition), 2014,26(1):1-5.
[6] BROWN G H, LY G N. Statistics for the number of fiber ends in a segment of a random assembly of aligned fibers[J]. Textile Research Journal, 1985,55(4):206-210.
[7] 严广松, 苏玉恒. 棉纱线中纤维头端的等效分布研究[J]. 河南工程学院学报(自然科学版), 2011,23(2): 1-5. YAN Guangsong, SU Yuheng. Study on the equivalent distribution of fiber ends in cotton yarns[J]. Journal of Henan Institute of Engineering(Natural Science Edition), 2011,23(2):1-5.
[8] JIANG Z, HU Y B, KUANG X Q, et al. Simulation on fiber random arrangement in the yarn[J]. The Journal of The Textile Institute, 2014,105(12):1312-1318.
[9] 严广松, 苏玉恒, 朱进忠. 纱线条干不匀的随机模拟[J]. 纺织学报, 2012, 33(1):33-37. YAN Guangsong,SU Yuheng, ZHU Jinzhong. Stochastic simulation of yarn unevenness[J]. Journal of Textile Research, 2012, 33(1):33-37.
[10] 上海纺织高等专科学校棉纺教研室.棉纺工程:上[M].北京:纺织工业出版社,1989:418-419. Teaching and Research Section of Shanghai Cotton Textile College. Cotton Textile Engineering: Volume One[M]. Beijing: Textile Industry Press,1989:418-419.
Distribution of fiber left ends in card sliver
ZHANG Hongqiang1, HU Yuanbo2, JIANG Zhan1, KUANG Xueqin1, YU Chongwen1,3
(1.CollegeofTextiles,DonghuaUniversity,Shanghai201620,China; 2.SchoolofFundamentalStudies,ShanghaiUniversityofEngineeringScience,Shanghai201620,China; 3.KeyLaboratoryofTextileScience&Technology,MinistryofEducation,DonghuaUniversity,Shanghai201620,China)
In order to further explore the fiber distribution and simulate the fiber arrangement in the sliver,the assumption that fibers left ends were uniformly distributed along the sliver axis in previous researches is required to verify by any experiment method. By counting the number of dyed tracer fibers contained in cotton sliver segment of given length, the verification was conducted usingχ2inspection method. It can be seen from the results that the hypothesis that fiber left ends arrangement in the sliver were uniformly distributed is reasonable. In addition, the varied geometrical natures, type of the dyed fiber and the different length of carded sliver segment are selected in the experiment. The results also indicate that the geometrical features have no significant effect on the distribution of fiber left heads in the sliver, as well as the fiber type and the length of carded sliver segment, which provides the basis for predicting sliver properties.
sliver; fiber arrangement; number of left end; uniform distribution
10.13475/j.fzxb.20150304404
2015-03-24
2015-12-04
国家自然科学基金资助项目(51173023)
张弘强(1990—),男,硕士生。研究方向为纺纱基础理论。郁崇文,通信作者,E-mail:yucw@dhu.edu.cn。
TS 101.1
A

