刚架拱桥的极限承载力研究

■　谢江平（福建省高速公路有限责任公司三明管理分公司，三明　365000）



刚架拱桥的极限承载力研究

■谢江平
（福建省高速公路有限责任公司三明管理分公司，三明365000）

摘要本文基于极限承载力分析的基本理论，以福建省尤溪县坪寨大桥为工程背景，采用ANSYS建立有限元模型，在同时考虑几何非线性、材料非线性及混凝土开裂特性的条件下分析极限承载力，并对刚架拱桥的破坏形式进行全过程研究。结果表明，刚架拱桥的极限承载力是以稳定控制为主，其破坏形式属于第二类弹塑性失稳破坏，安全储备较低，耐超载能力较差。

关键词刚架拱桥极限承载力几何非线性材料非线性

1　引言

刚架拱桥是在我国传统的双曲拱桥、桁架拱桥的基础上结合斜腿刚构的特点发展演变而来的一种桥型，属于有推力的高次超静定结构，其受力兼有拱与梁式刚架的特性，从力学性能和经济性上都较传统的梁式和拱式结构为优［1］。随着计算理论的完善、施工工法的进步以及计算机辅助设计技术的应用，刚架拱桥不仅在跨径上有所突破，而且在桥型上也发展出了新的形式。

目前，综合考虑结构几何、材料非线性影响的弹塑性分析理论被广泛运用于拱桥结构极限承载力分析［2-6］，计算出的临界荷载能较真实地反映结构的承载能力，但关于刚架拱桥的极限承载力系统性研究还是空白，因此，对刚架拱桥的极限承载力进行研究具有重要的现实意义。

2　有限元模型建立及若干问题处理

2.1工程背景

本文以福建省尤溪县坪寨大桥为工程背景，采用ANSYS软件建立有限元分析模型。坪寨大桥全桥总长210.72米，共分三跨，跨径布置为63.625m+63.6m+ 63.625m，桥梁全宽12m，其中主车道9m，两侧人行道各宽1.5m，两侧栏杆各宽0.25m，设计荷载为汽车-20、挂车-100，矢跨比为1/8，正交直桥。

2.2有限元模型

钢筋混凝土模型采用整体式模型即将钢筋弥散于整个单元中，把钢筋混凝土单元视为一个综合的整体单元，全桥共划分Solid65单元3928个，Solid45单元3150个，共有节点16373个，建立的有限元模型如图1所示。

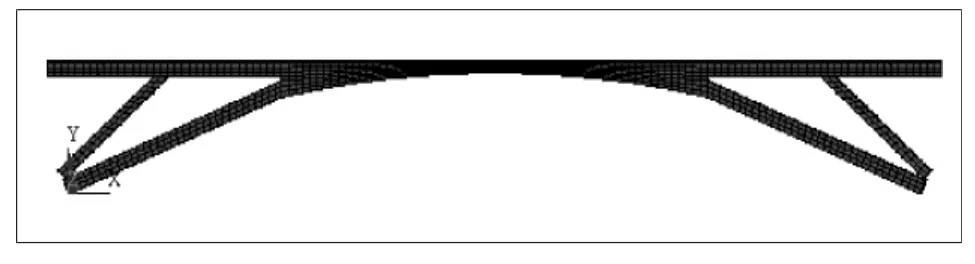
图1　刚架拱桥有限元模型

2.3若干问题处理

为了提高计算速度和减小分析的复杂程度，本文提出若干假设，对模型进行了必要的简化：

（1）忽略连拱效应，取其中一跨模型进行分析，减少了模型的单元总数和分析的复杂程度。

（2）边界条件的模拟：忽略桥墩与桥台的位移，并以相应的约束代替桥墩与桥台的作用，其中拱腿与斜撑均为固结，弦杆约束竖向和横桥向的位移。

（3）混凝土的本构关系采用E．Hongnestad曲线；钢筋的本构关系采用理想刚塑性模型。

（4）采用恒截+全桥均布荷载（工况1）、恒截+半桥均布荷载（工况2）、恒截+半侧均布荷载（工况3）三种加载工况，并且根据等代荷载法将集中荷载换算成全桥均布面荷载，计算出各工况的初始设计活荷载集度为：工况1=4.26kN/m2；工况2=8.51kN/m2；工况3=8.51kN/m2。

3　刚架拱桥的极限承载力分析

3.1双重非线性分析

同时考虑结构的材料非线性和几何非线性因素，并考虑混凝土的开裂特性，通过荷载增量法和迭代法相结合的方法求解结构的极限承载力。分析中考虑了恒载和活荷载的作用，其中活荷载按初始活荷载逐级增加。在三种荷载工况作用下，拱顶截面的活荷载系数－位移曲线如图2～4所示：

图2　工况1作用下拱顶荷载－位移曲线

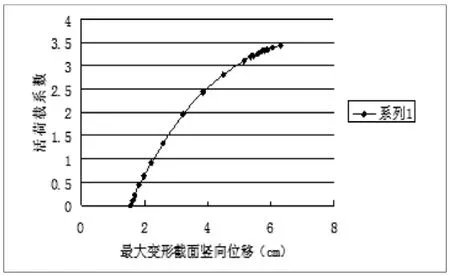
图3　工况2作用下拱顶荷载－位移曲线

图4　工况3作用下拱顶荷载－位移曲线

三种荷载工况下计算所得结构极限活荷载系数分别为λ1=6.15，λ2=3.440，λ3=3.580。

结果表明：一般拱桥的失稳破坏是发生面内反对称失稳，而刚架拱桥在横向偏载作用下横向稳定性较差，由此可见刚架拱桥横向联系的重要性。

3.2刚架拱桥破坏的全过程研究

一般来说，第二类弹塑性失稳发生于下列两种情况的交叉影响：（1）在荷载逐渐增加的过程中，结构的位移随之逐渐增大，当在施加微小增量荷载时，结构即发生大幅度变形而不能使用；（2）在加载过程中，某些杆件由于超过屈服应力而退出工作，导致结构刚度减小，直到退化为几何可变体系。因此，在变形渐大、构件应力渐增，发生局部屈服杆件数目不断增多的联合作用下，最终导致结构整体失稳。

3.2.1荷载工况1作用下结构破坏的全过程研究

当活荷载系数达到6.21时，拱桥发生第二类失稳破坏，即此时荷载达到稳定极限荷载值，相对应的最大挠度发生在拱顶（L/2拱）处，其值为7.775cm。模拟全过程结果如下：当活荷载系数值为1.896时，最大挠度发生在拱顶，位移值为2.799cm，各构件均处于弹性状态，相对而言，拱顶周围、主拱腿特别是大节点附近以及拱脚附近，应力较大，但均未达到屈服强度；在横系梁与刚架拱片交接处存在明显的应力集中现象。随着荷载的增大，跨中桥面板最先进入塑性，大节点附近的主拱腿下缘随后也进入塑性阶段；随着荷载的继续增大，跨中桥面板的塑性向两侧发展，大节点的主拱腿附近下缘的塑性也向两侧及上缘发展，当达到极限荷载时，跨中桥面板塑性区进一步扩大，在很小的荷载增量作用下结构就发生较大变形，导致结构坍塌。图5为结构破坏时全桥的裂缝发展情况。

图5　工况1作用下结构破坏时裂缝发展情况

3.2.2荷载工况2作用下结构破坏的全过程研究

本工况模拟拱桥塞车时的不利状况。当活荷载系数达到3.440时，拱桥发生全桥面内反对称失稳破坏。破坏时由于加载的另一侧主梁下缘的混凝土应力最大，发生压溃，全桥变形很快增大，全桥面内反对称失稳破坏。竖向的最大变形发生在加载一侧大节点与拱顶之间的截面上，最大变形值达到6.313cm。模拟全过程结果如下：在荷载作用的初期阶段，加载的另一侧位于跨中与大节点之间的主梁下缘应力、横系梁（特别是加载的另一侧）与刚架拱片的连接处应力最大；随着荷载的继续增大，未加载一侧的主梁下缘的应力最先达到屈服强度，进入塑性，而另一侧主梁的应力应变仍然非常小，荷载的继续增大使得位于未加载一侧的位于跨中与大节点之间的主梁下缘的混凝土被压溃，在很小荷载作用下，结构变形增长很快，最后发生全桥面内反对称失稳破坏。图6为结构破坏时全桥的裂缝发展情况。

图6　工况2作用下结构破坏时裂缝发展情况

图7　工况3作用下结构破坏时裂缝发展情况

3.2.3荷载工况3作用下结构破坏的全过程研究

本工况模拟拱桥塞车时的不利状况。在半侧均布活荷载作用下，当活荷载系数达到3.580时拱桥发生面外失稳破坏，相对应的最大挠度发生在加载侧跨中桥面板处，其值为9.336cm。模拟全过程结果如下：加载的全过程，加载侧的最外侧一刚架拱片受力相比其它拱片都是最大的，离加载侧越远的刚架拱片应力就越小。随着荷载的增加，跨中加载侧最外沿桥面板达到屈服强度，进入塑性状态，并随着荷载的增加向周围发展，随后靠近加载侧的最外沿的刚架拱片的大节点附近也进入塑性阶段，而离其越远的拱片受力就越小，甚至处在弹性工作阶段，正是这种应力分布状况导致结构破坏时，加载侧的最外沿的刚架拱片跨中桥面板的混凝土被压溃，然后整跨结构向侧倾方向歪扭，发生横向面外失稳破坏。图7为结构破坏时全桥的裂缝发展情况。

综合三种荷载工况作用下结构的破坏全过程研究可以看出：此类较大跨度的钢筋混凝土刚架拱桥，具体的破坏形式与活荷载作用形式有很大关系。总的来说，这类拱桥的破坏形式属于第二类弹塑性失稳破坏，而且破坏前有一定的征兆，如塑性区的开展等。

3.3背景桥梁的稳定安全系数

一般拱桥的破坏形式为第二类弹塑性失稳破坏，即结构整体失稳破坏之前，局部己经发生强度破坏，而且稳定破坏更具严重性，故对于合理的结构设计来说，要求结构的强度破坏早于稳定破坏出现。这就要求拱桥安全系数的最低容许值应该大于强度问题的安全储备。

按照《公路桥涵钢结构及木结构设计规范》的容许应力计算时，安全系数是K＞1.70。因此，拱桥稳定安全系数的最低容许值不应该低于1.70，背景桥梁稳定安全系数略大于按容许应力计算的安全系数容许值。

4　结论

本章对背景桥梁进行了线弹性稳定分析和第二类稳定性分析，并对拱桥极限承力的三种分析方法作了分析比较；文章着重在考虑双重非线性因素影响下，对该结构的破坏过程和破坏形式进行全过程研究。通过分析研究，得出以下结论：

（1）刚架拱桥的横向稳定性较差，主拱腿易发生局部失稳现象。当横向联系不足时，横桥向偏载的作用容易产生横桥向面外失稳破坏。

（2）对于刚架拱桥，破坏形式属于第二类弹塑性失稳破坏，破坏前有一定的征兆，如塑性区的开展等。

（3）经承载力验算，背景桥梁基本满足设计荷载的安全性要求，但耐超载能力较差。

参考文献

［1］姚玲森．桥梁工程．北京：人民交通出版社，1985．

［2］张建民，郑皆连，肖汝诚．钢管混凝土拱桥的极限承载力分析．中南公路工程，2004．

［3］张建民，肖汝诚．巫峡长江大桥极限承载能力分析．公路交通科技，2004，21（2）：37-40．

［4］程进，江见鲸．拱桥结构极限承载力的研究现状与发展．公路交通科技．2002，19（4）：57-59．

［5］金伟良．钢筋混凝土拱桥的极限承载力．浙江大学学报．1997，31 （4）：449-461．

［6］李松，强士中，唐英．钢筋混凝土拱桥极限承载力的参数研究．西南交通大学学报，2006，42（3）：293-298．