一道错题引发的思考

王　璐

(浙江省嘉兴市第一中学，314000)



一道错题引发的思考

王璐

(浙江省嘉兴市第一中学，314000)

数学是研究现实世界的数量关系和空间形式的一门科学，它的基本特点是应用的广泛性、抽象性和严密性(即逻辑严密、结论精确).作为一线数学教师我们发现每每问及学生发生错解、漏解的原因时,他们最常说的一句话是“我想不到啊”.培养学生“思维严密性”是高中数学的基本学习目的,也是高考的一个主要考察方向.它体现在各种各样的问题中,比较典型的如“分类讨论”等,它是检验学生“思维严密性”的一个很好的载体.虽然说培养思维的严密性是数学学习的基本目的,但是很多学生终其三年都很难有所领悟,更别说运用自如了.

一、因“错”而起

1. 将错就错

笔者在解析几何的教学时,在配套学案中发现如下一个题,确切地说是一个错题:

引例已知点M(-3,0),N(3,0),B(1,0),动圆C与直线MN切于点B,过M,N与圆C相切的两直线相交于点P,则P点的轨迹方程为()

笔者把这道题交给学生,让他们当堂来解,并要求有解题过程.

笔者进一步提问,大家在解题的过程中有没有发现什么问题?学生思考之后有个别数学基础扎实的同学发现了问题.

2.刨根问底

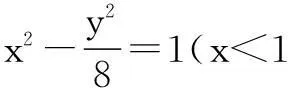
出现漏解的原因,主要还是对于本题中直线与圆相切的情况考虑不充分,使其所作出的图形只反映了其中一种情况而忽略了另外一种可能,其根仍在于“思维严密性”的欠缺.

二、寻根“错结”

那么，如何才能提高学生的思维严密性,使他们能比较轻松地应对这样或那样的数学问题,从而减少错解漏解呢?笔者认为，首先要提高学生对于所学知识的熟悉程度,只有对非常熟悉的东西我们才有可能考虑到它的方方面面,才有可能实现“思维的严密性”.其次要对经常出现错漏的原因分类明确,对于学生反映出来的各种各样的错误进行归类,并组合到自己的教学中去,让学生多见多想,开拓眼界.以下是笔者所作的一些归纳:

1. 部分图象缺漏

这种情况在引例中已经具体阐述过,但是要想防止这一类问题,提高解题严密性,最重要的还是要加强对于这类“隐秘”问题的常规训练,让学生多见多想才能起到好的效果.我们再给出一例.

5月8日，毛泽东再次收到胡乔木当天的来信。信中说，韶山公社食堂已由原有的112个减为6个，其中5个不久都将不办。对于在短短的3天时间内基本解决全公社的食堂问题，群众反应热烈的程度难以想像，有的甚至说这是“第二次解放”。预计最近即可在湖南全省范围内解决。9日，毛泽东转发了此信，认为很有用［2］489－490。

例1已知函数f(x)=|x2+3x|,x∈R.若方程f(x)-a|x-1|=0恰有4个互异的实数根,则实数a的取值范围为______.

这个问题解决的时候我们经常会考虑函数f(x)=|x2+3x|与函数g(x)=a|x-1|公共点个数,在处理上学生经常会画如图3的图形.

这时得到的a的取值范围为09

2. 定义理解不透

3. 忽略隐含条件

有时题目中的条件可以反复运用,而往往条件用过一次之后,学生就不再去细“挖”,造成结果出错或者是出现增根.

(*)

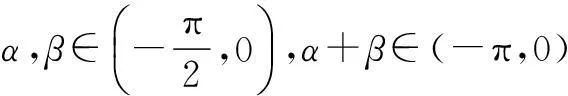
忽略了隐含条件,其结果自然是出现错误,这也是思维不严密的一种体现,因此思考问题时要尽量细致严谨,注意挖掘隐含条件.

4. 审题草率不清

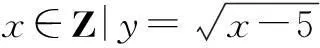
高中数学对于学生思维的严密性提出了较高的要求.数学思维严密的学生,对所学知识的本质有深刻的理解,对知识之间的联系有较好的把握,善于全面地分析问题,摆脱固有模式的束缚,最大限度地避免错解、漏解.因此，教师应在平时的教学中可以有意识地多收集同类问题并对学生的思维加以指导,精心设置问题,灵活变换,从一些简单的或者类似的问题入手，让他们习惯于在解决问题时要考虑到问题的方方面面,引导学生发现问题的本质联系,培养学生思维的严密性.