谐振腔微扰法测量材料复介电常数的仿真研究
牛金民,李旭东,唐园亮
(兰州理工大学 有色金属先进加工与再利用省部共建国家重点实验室,甘肃 兰州 730050)
谐振腔微扰法测量材料复介电常数的仿真研究
牛金民,李旭东,唐园亮
(兰州理工大学 有色金属先进加工与再利用省部共建国家重点实验室,甘肃 兰州730050)
摘要通过对谐振腔微扰法的理论分析,利用电磁仿真软件求解材料微波频段的复介电常数。在软件中分析谐振腔与样品的网格单元尺寸对结果的影响,求出最优解的网格单元尺寸作为其标准用来实现微波频段的多频点测量,并进行叠层型两相复合材料的仿真预测。结果表明:在多频点测量准确度较高,并对预测复合材料的复介电常数具有一定的指导性。
关键词谐振腔;复介电常数;微扰法;复合材料
随着科技的进步,电子产业正在向高频化、宽工作频带、高传输速度方向发展,该趋势促进了高频微波材料的发展,这就对微波介质材料提出了更高的要求[1,2],更为准确地知道被测介质材料的微波复介电常数显得尤为重要[3-6]。
当频率高达微波频段时,集中参数的电容与电感失去了意义,普通的谐振电路就不能再用,而要采用由金属导体组成封闭的、且具有一定几何形状的空间作为微波频段的电磁波的谐振回路,称之为谐振腔。在谐振腔中某些物理条件的微小变化,如腔内引入小体积的介质等,这些物理条件的改变所引起的微小扰动,将会导致谐振腔的谐振频率、品质因数等参量相应地发生微小变化,这种微小变化被称为“微扰”。这时可使用微扰法求解,即根据变化前的未微扰值(原来物理量)和变化后的扰动值(变化后物理量)来计算谐振腔中参量的改变量,从而获得所需要的近似解。
1理论基础
在工程测量中,需要确定的电磁参量便是电介质材料的介电常数的值和损耗角正切的值。在外场作用下,介质材料将其中一部分电能转化为热能的物理过程,即介质材料本身的发热,使得温度上升,称为电介质的损耗[7]。介质损耗主要由电导损耗、极化损耗和谐振损耗引起,其中电介质材料的微波介电常数一般为复数:
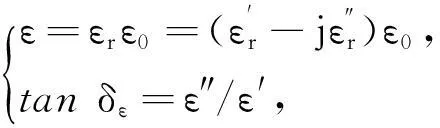
(1)
其中:εr为相对介电常数;ε0为真空介电常数;tanδε为介电损耗角正切。
矩形谐振腔就是将两端封闭的矩形波导加上输出藕合装置与激励组成,是横截面为矩形的空心金属管。将电磁波输入谐振腔中,电磁波便在两端板间不断往复反射。要使电磁波在腔中产生谐振,调整两端板间距离即可,也就是说腔内产生半波长整数倍的驻波。
从广义上来讲,波导是指用来引导电磁波进行传输的一种系统,按照所传输的电磁波的波形来划分,波导被分为四种类型:表面波传输型、横电磁波(TEM 波)传输型、横电波(TE 波)传输型和横磁波(TM波)传输型[8],其中矩形波导就是横截面为矩形的空心金属管。为了增强其导电性能以及减少损耗,管壁一般都是由铜或者铜合金制成。
由一段两个端面封闭的矩形波导,再加上适当的输出耦合与激励装置,就构成一个矩形谐振腔,如图1所示。该矩形腔宽边长为a,窄边长为b ,长边长为c,其中长边两端面用金属板短路,形成了一个封闭的空腔,电能与磁能就储藏在腔内部。将样品放入谐振腔中,从而在放入样品前后形成微扰。
在矩形谐振腔存在着无穷多个横电波传输型振荡模,用TEmnp表示。其下标m、n、p 均为自然数,分别表示了在场分量中沿 x、y、z 方向变化的半个驻波个数。对于TEmnp振荡模,其谐振频率为

(2)
其中:a、b、c为谐振腔的宽、高、长;μ为谐振腔内介质的磁导率;ε为腔内介质的介电常数。
Carter R[9]介绍了谐振腔的微扰理论。设有一谐振腔,腔内充介质(其介电常数为ε,磁导率为μ),则腔内电磁场向量E0、H0满足Maxwell方程:
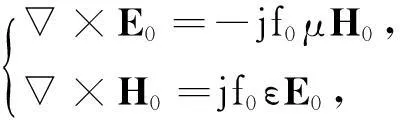
(3)
其中:f0为固有频率。若其介质参数变为(ε+Δε)、(μ+Δμ),则场的固有频率相应地变为f=f0+Δf,这时腔内电磁场向量E、H同样满足Maxwell方程:
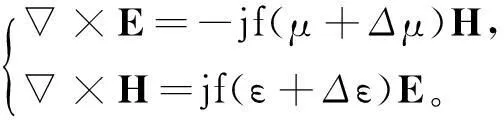
(4)
在放进样品后,除样品所在处的电磁场发生变化外,腔内其他地方的电磁场变化很小,可认为电磁场的变化保持不变,则可得到谐振腔的微扰公式:
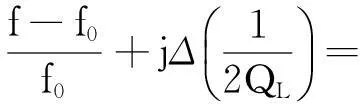
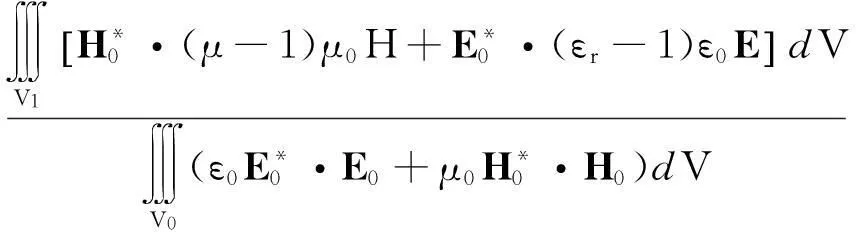
(5)
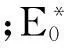
从以上公式得到谐振腔在加载样品前后的谐振频率与品质因数,从而计算出介电常数为
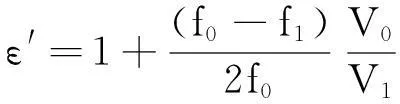
(6)
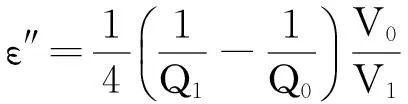
(7)
其中:ε′为介电常数实部;ε″为介电常数虚部;f0为空腔谐振频率;f1为加载样品后的谐振频率;V0为谐振腔体积;V1为样品体积;Q0为空腔品质因数,Q1为加载样品后的品质因数。
2矩形谐振腔设计
有限元软件ANSYS中的电磁模块就是以麦克斯韦方程组为理论基础,通过电磁场的有限元[10,11]计算,得到电磁相关的参量。以 10 GHz 谐振腔为例,使用ANSYS进行仿真。选取BJ100波导为研究对象,则其宽度a=22.86 mm,高度b=10.16 mm。
选择传输类型为TE10p(p为奇数),根据式(2)可求出当p取不同值时谐振腔的长度c值。选取矩形杆样品放入谐振腔中以形成微扰。依据标准[12],矩形样品横截面积大小为
A=wd=d2=a2/900,
(8)
其中:w表示矩形截面的长度;d为矩形截面的宽度。另外在仿真模拟中取样品的高度为谐振腔高度。可求出样品长度w=0.762 mm,高度b=10.16 mm,宽度d=0.762 mm。
腔体内部填充物质为空气,其相对介电常数与相对磁导率都为1。样品选取环氧树脂,根据实验数据样品环氧树脂在微波频段的相对介电常数为2.75,相对磁导率为1,损耗角正切为0.03。即介电常数实部为2.75,介电常数虚部为0.082 5[13]。
研究将谐振腔与样品划分为几组不同大小的网格尺寸,通过仿真研究求出最优解。网格类型为四面体网格,谐振腔网格单元尺寸为0.5 mm,样品的网格单元尺寸为0.1 mm。求出谐振腔加载样品前后的谐振频率与品质因数,根据式(6)、式(7)计算出样品环氧树脂的复介电常数。表1表示在该网格单元下p取不同值时材料的复介电常数误差。
根据仿真结果,可知在该网格尺寸下,p的取值对结果的影响较小,且整体误差都在3%以内,则仿真结果的准确性较高。另外当p=13时结果误差相对较小,则可选取这组网格下p=13的谐振腔做为标准对其他频率下的谐振腔进行网格划分,以减小所求结果的误差,从而实现在微波频段下材料的多频点测量。
令谐振腔的四面体网格单元体积为Ve1,谐振腔体积为V0;样品的四面体网格单元体积为Ve2,样品体积为V1。以10 GHz下p=13的谐振腔的网格划分作为标准,有
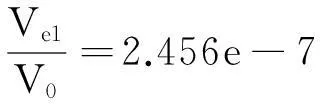
(9)
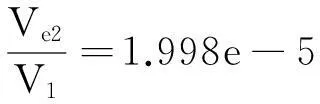
(10)
在2 GHz选择p=9的谐振腔计算,选取BJ22波导为研究对象,则谐振腔宽度a=109.22 mm,高度b=54.01 mm,长度c=927.8mm。由式(9)得谐振腔网格单元尺寸为2.26 mm,测得空腔的谐振频率f0为1.999 3 GHz,空腔品质因数Q0值为24 101.135 3。将长度为3.64 mm,高54.61 mm,宽3.64 mm的样品环氧树脂放入谐振腔正中央,由式(10)得样品的网格单元尺寸为0.5 mm。测得腔的有样谐振频率f1为1.998 4 GHz,品质因数Q1为11 858.523 2。利用式(6)、式(7) 计算出样品的介电常数实部为2.69,误差为2.2% ;介电常数虚部为0.081 87,误差为0.76% 。
在20 GHz选择p=13的谐振腔计算,选取BJ220波导为研究对象,则谐振腔宽度a=10.688 mm,高度b=4.318 mm,长度c=136.736 mm。由式(9)得谐振腔网格单元尺寸为0.236 mm,测得空腔的谐振频率f0为19.992 6 GHz,空腔品质因数Q0值为6 453.989 8。将长度为0.356 mm,高4.318 mm,宽0.356 mm的样品环氧树脂放入谐振腔正中央,由式(10)得样品的网格单元尺寸为0.045 mm。测得腔的有样谐振频率f1为19.986 8 GHz,品质因数Q1为5 467.982 8。利用式(6)、式(7)计算出样品的介电常数实部为2.67,误差为2.9% ;介电常数虚部为0.081 12,误差为1.67% 。
由以上可知计算结果在误差所允许的范围内,从而验证了该方法在微波频段进行多频点电磁参数测量的可行性。
3复合材料的仿真
对于两相复合材料,最基本的有2-2型叠层材料,其复合性能为横向各向同性。假设两种介质(组分材料)A和B的体积含量分别为VA和VB,而其介电常数实部分别为εA和εB,损耗角正切分别为tanδA和tanδB,A和B的混合介质(复合材料)的介电常数实部为ε,损耗角正切为tanδ。混合介质板处于平行于板的电场中,则其符合等效并联RC电路,从而可求得[14]
ε=VAεA+VBεB,
(11)
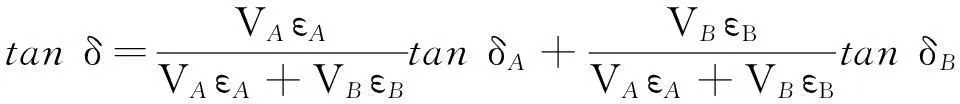
(12)
为了验证预测方法的正确性,先建立了叠层材料的数学模型,赋予不同的材料属性,用前述方法进行预测。将基体材料的介电常数实部设为2,损耗角正切设为0.1。增强相的介电常数实部设为5,损耗角正切设为0.01。令增强相的体积成倍增加,基体体积成倍减小,从而求出在不同体积分数下的介电常数与损耗角正切。图2表示2-2型叠层材料的模型。
图3和图4分别表示2-2型叠层材料的介电常数实部与虚部在F不断增加时,其理论值与模拟值的对比图,F表示增强相所占整体复合材料的体积分数。其中图3横坐标F表示增强相所占整体复合材料的体积分数,纵坐标ε′表示复合材料介电常数的实部。理论计算表示2-2型叠层材料介电常数的理论计算值,有限元方法表示运用有限元计算2-2型叠层材料介电常数时所得到的结果。图4的横坐标F表示增强相所占整体复合材料的体积分数,纵坐标ε″表示复合材料介电常数的虚部。
对比分析图3与图4可知,对于2-2型叠层材料,研究预测的介电常数实部和虚部与理论值基本重合,验证了此方法在预测复合材料复介电常数的可行性。
4结论
研究利用谐振腔微扰理论在电磁仿真软件中的模拟计算得到材料在微波频段的复介电常数,并且找到一种网格标准实现材料复介电常数的多频点测量。通过模拟2-2型叠层材料,得到该复合材料的模拟结果与理论公式计算结果相差较小,验证了此方法预测复合材料复介电常数具有较高的准确度,从而在复合材料复介电常数的预测上找到一种较为简单的方法。
参考文献:
[1]李文兴.高Q值、高稳定微波介质陶瓷材料制作方法的研究[J].电子设计工程,2013,21(11):69-70.
[2]李佶莲,傅仁利,徐越,等.Ba2Ti9O20基微波介质陶瓷的微观组织与微波介电性能[J].电子元件与材料,2014,33(7):12-15.[3]彭显旭.磁性纳米膜微波磁谱测量系统研究[D].武汉:华中科技大学,2006.[4]Daiqing L,Charles F.A Simple Method for Accurate Loss Tangent Measurement of Dielectrics Using a Microwave Resonant Cavity[J].IEEE Microwave and Wireless Components Letters,2001,11(3):118-120.
[5]王国金.微扰法在微波谐振腔中的应用研究[J].宁夏大学学报:自然科学版,2002,23(1):50-52.
[6]Kraszewski A W,Nelson S O.Observations on Resonant Cavity Perturbation by Dielectric Objects[J].IEEE Trans Microwave Theory Tech,1992,40(1):151-155.
[7]邱四伟.介质损耗测量仪的设计与实验[D].成都:电子科技大学,2012.
[8]廖承恩.微波技术基础[M].西安:西安电子科技大学出版社,2000.
[9]Carter R.Accuracy of Microwave Cavity Perturbation Measurements[J].IEEE Trans MTT,2001,49(5):918-923.
[10]金建铭.电磁场有限元方法[M].西安:西安电子科技大学出版社,2001.
[11]陈君辉,杨逢瑜,李正贵,等.基于有限元法的异步变频电机失磁运行转子的涡流损耗计算[J].甘肃科学学报,2012,24(1):127-130.
[12]成都电讯工程学院.GB/T 7265.1-1987固体电介质微波复介电常数的测试方法—微扰法[S].北京:中国标准出版社,1987.
[13]张振华.复合材料结构与介电特性的相关性研究[D].海口:海南大学,2012.
[14]曾竟成,罗青,唐羽章.复合材料理化性能[M].长沙:国防科技大学出版社,1998.
Simulation Study on Material Measurement of Complex Permittivity by Cavity Perturbation Method
Niu Jinmin,Li Xudong,Tang Yuanliang
(State Key Laboratory of Advanced Processing and Recycling of Nonferrous Metals,Lanzhou University of Technology,Lanzhou 730050,China)
Key wordsResonant cavity;Complex permittivity;Perturbation method;Composites
AbstractSolution of complex permittivity of material in microwave frequency band can be deduced by a theoretical analysis of cavity perturbation method and using electromagnetic simulation software.Multi-frequency point measurement of microwave frequency band is accomplished and simulation and forecast of laminated two-phase composite are conducted by taking sizes of grid cell of optimal solution as its standards,which is deduced from analysis of influence of sizes of grid cell of resonant cavity and samples on results in software.The results indicate that measurement on multi-frequency point has higher accuracy which have a certain guidance on forecast of complex permittivity of composites.
doi:10.16468/j.cnki.issn1004-0366.2016.03.018.
收稿日期:2015-03-24;修回日期:2015-03-25.
作者简介:牛金民(1988-),男,甘肃会宁人,硕士研究生,研究方向为材料电磁性能.E-mail:niujinmin123@126.com. 通讯作者:李旭东.E-mail: lixd@lut.cn.
中图分类号:TM934.33
文献标志码:A
文章编号:1004-0366(2016)03-0085-05
引用格式:Niu Jinmin,Li Xudong,Tang Yuanliang.Simulation Study on Material Measurement of Complex Permittivity by Cavity Perturbation Method[J].Journal of Gansu Sciences,2016,28(3):85-88,112.[牛金民,李旭东,唐园亮.谐振腔微扰法测量材料复介电常数的仿真研究[J].甘肃科学学报,2016,28(3):85-88,112.]

