带注资和交易费用的扩散模型的最优分红
岳毅蒙,王 欣,赵 锐
(1.商洛学院 数学与计算机应用学院,陕西 商洛 726000;
(2.商洛学院 经济与管理学院,陕西 商洛 726000)
带注资和交易费用的扩散模型的最优分红
岳毅蒙1,王欣2,赵锐1
(1.商洛学院 数学与计算机应用学院,陕西 商洛726000;
(2.商洛学院 经济与管理学院,陕西 商洛726000)
摘要在带注资和交易费用的扩散模型基础上,以股东的折现分红减去惩罚折现注资的差的期望值最大化为目标,讨论了模型的最优分红策略问题。由随机控制理论建立相应的HJB方程,得到了相应的解及最优分红策略。
关键词扩散模型;注资;HJB方程;分红
分红问题最早是由De Finetti在1957年精算大会上首次提出,随后便成为许多学者研究讨论的热点问题。文献[1]中讨论了最小盈余下经典风险模型的最优分红和注资策略。文献[2]中讨论了带注资和管理费用的风险模型的最优分红和注资策略。我们在前人研究[3-11]的基础上,讨论带注资和交易费用扩散风险模型的最优分红问题,为保险公司的分红和注资提供一定的理论指导作用。
1模型构建


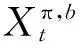

动态方程可描述为


(1) {Dt}是右连左极的,增的适应的过程,且满足D0-=0;
(2) {Zt}是左连右极的,增的适应的过程,且满足Z0=0。
假设保险公司有最低盈余要求m>0,如果赤字太大,注资不合理,破产时刻定义为

对每个可行策略(D,Z,π,b),定义性能指标:

其中:β<1是分红交易费用的比例因子;δ>0是折扣因子;φ>1是罚金因子。我们的目标就是最大化V(D,Z,π,b)(x),定义值函数:
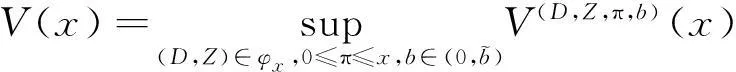
则盈余过程转化为

只考虑有约束的分红策略,即假设分红率为Ut,且

0≤Ut≤u0<∞。
2HJB方程和最优策略
引理1值函数V(x)在[a,∞)上是凹函数。

类似于文献[3],我们可以得到HJB方程:
(θ-η)μ-u]V′(x)+βu-δV(x)+

(1)
其中:u是线性的,所以最优分红策略应满足:
(2)
其中:x0∶=inf{x∶V′(x)≤β}。
证明由f是增的、有界的,假设f收敛到f(∞)<∞。这里存在xn→∞满足f′(xn)→0。令un=u(xn),由最优分红策略的定义,假设un=u0,令n→∞,得到
0=[mπ+λ[θE(r(Y,b))-(θ-η)μ]+βu0-
βu0-δf(∞),
现令U=U*表示由式(2)给出的分红策略,相应的Z*=ZU*。由引理和HJB方程可得
是一个期望为0的鞅。所以




令t→∞,则f(x)≥VU(x)。
所以f(x)=V(x)。
3结语
在扩散模型的基础上考虑注资和交易费用因素,利用随机控制理论求出相应的解及最优分红策略。这一研究推广了前人的理论,使风险模型更加符合实际,更具现实意义,这些结论能为保险公司的稳健性经营提供理论支持。
参考文献:
[1]李岩.经典风险模型中最优分红与注资及最优再保险策略的研究[D].长沙:中南大学,2009.
[2]Scheer N,Schmidli H.Optimal Dividend Strategies in a Cramer-Lundberg Model with Capital Injections and Administration Costs[J].European Actuarial Journal,2011,1(1):57-92.
[3]Schmidli H.Optimal Dividend Strategies in a Cramer-LundBerg Model with Capital Injections[J].Insurance:Mathematics and Economics,2008,5:1-9.
[4]Hunting M,Paulsen J.Optimal Dividend Policies with Transaction Costs for a Class of Jump-diffusion Processes[J].Finance and Stochastics,2013,17(1):73-106.
[5]Zhu J.Optimal Dividend Control for a Generalized Risk Model with Investment Incomes and Debit Interest[J].Scandinavian Actuarial Journal,2013,(2):140-162.
[6]Eisenberg J,Schmidli H.Optimal Control of Capital Injections by Reinsurance in a Diffusion Approximation[J].Blätter Der DGVFM,2009,30(1):1-13.[7]Eisenberg J,Schmidli H.Minimising Expected Discounted Capital Injections by Reinsurance in a Classical Risk Model[J].Scandinavian Actuarial Journal,2011,(3):155-176.[8]Gerber H U,Shiu E S W.On Optimal Dividend Strategies in the Compound Poisson Model[J].North American Actuarial Journal,2006,10(2):76-93.
[9]戴晓枫.带有投资和再保险的分红及资产注入的最优控制[D].北京:清华大学,2011.
[10]Avram F,Palmowski Z,Pistorius M R.On the Optimal Dividend Problem for a Spectrally Negative Lévy Process[J].The Annals of Applied Probability,2007,17(1):156-180.
[11]岳毅蒙.最小盈余约束下风险模型的最优分红策略[J].甘肃科学学报,2015,27(2):19-24.
Optimal Dividends of Diffusion Model with Capital Injection and Transaction Cost
Yue Yimeng1,Wang Xin2,Zhao Rui1
(1.Faculty of Mathematics and Computer Application,Shangluo University,Shangluo 726000,China;2.Faculty of Economics and Management,Shangluo University,Shangluo 726000,China)
Key wordsDiffusion model;Capital injection;HJB equation;Dividends
AbstractIssues about optimal dividends strategies of the model are discussed based on diffusion model with capital injection and transaction cost and by realizing the difference of maximization of value of expectation which equals to discounted dividends of shareholders minus punishment discounting capital injection as a target.The corresponding solutions and optimal dividend strategies are deduced through related HJB equation built by stochastic control theory.
doi:10.16468/j.cnki.issn1004-0366.2016.03.003.
收稿日期:2015-08-17;修回日期:2015-10-09.
基金项目:陕西省教育科学“十二五”规划课题(SGH13406);商洛学院科研项目(15SKY011).
作者简介:岳毅蒙(1984-),男,陕西富平人,硕士,讲师,研究方向为金融数学.E-mail:18740586401@126.com.
中图分类号:O211.6
文献标志码:A
文章编号:1004-0366(2016)03-0013-03
引用格式:Yue Yimeng,Wang Xin,Zhao Rui.Optimal Dividends of Diffusion Model with Capital Injection and Transaction Cost[J].Journal of Gansu Sciences,2016,28(3):13-15.[岳毅蒙,王欣,赵锐.带注资和交易费用的扩散模型的最优分红[J].甘肃科学学报,2016,28(3):13-15.]

