线性二次型最优控制在双关节机械手中的应用

刘中冬,林佳佳

(青岛科技大学 自动化与电子工程学院,山东 青岛　266061)



线性二次型最优控制在双关节机械手中的应用

刘中冬,林佳佳

(青岛科技大学 自动化与电子工程学院,山东 青岛266061)

摘要首先对双关节机械手系统建立数学模型并对此系统在平衡点处进行线性化处理,进而使用线性二次型最优控制的控制策略对双关节机械手系统进行控制,最后使用Matlab进行仿真以检验该控制系统的控制性能。阶跃输入下,系统能够在0.13 s完全跟踪。仿真结果表明其具有很好的响应能力及跟踪能力。

关键词双关节机械手；线性二次型最优控制；Matlab

双关节机械手系统[1-3]具有多变量、非线性[4,5]、强耦合、不确定等特性,由于其动态模型的复杂性,控制双关节机械手系统是一项艰难的任务,人们多采用现代控制理论的方法进行控制[6]。

现代理论中的线性二次型最优控制理论对系统的不确定性具有很好的稳定性和鲁棒性,但是线性二次型最优控制的被控对象是线性系统,为了将双关节机械手系统与线性二次型最优控制有效地结合,需要对非线性系统进行线性化处理。

运用线性二次型最优控制理论对双关节机械手系统的LQR方法进行了研究,提出的方法具有很好的跟踪能力及控制性能,最后通过仿真进行验证。

1双关节机械手系统建模

双关节机械手系统如图1所示。

双关节机械手的动力学方程的封闭形式为

(1)

所以

其中:

Δ=d22d11-d122;

d12=m2(lc22+l1lc2cosθ2)+I2;

d22=m2lc22+I2;

d11=m1lc12+m2(l12+lc22+2l1l2cosθ2)+

I1+I2;

φ1=(m1lc1+m2l1)gcosθ1+m2lc2gcos (θ1+θ2);

φ2=m2lc2gcos (θ1+θ2)。

d22(τ1-φ1)-d12(τ2-φ2)=0,

d11(τ2-φ2)-d12(τ1-φ1)=0。

2线性二次型最优控制

最优控制器的实质是确定一个最优控制u(t),使得系统从初始状态x(t0)转移到终端状态x(tf)时能够使得性能指标J为极大值或者极小值。此时的u(t)称为最优控制作用,所得的x(t)称为最优状态轨线,J称为最优性能指标。

线性系统的状态空间表示为

(2)

其中:A,B,C,D为适当维数的常数矩阵[7],线性二次型性能指标为

(3)

其中:Q为半正定对称时变加权矩阵;R为正定对称时变加权矩阵。Riccati方程为

ATP+PA-PBR-1BTP+Q=0,

(4)

u=-Kx,

(5)

(6)

假设(Q,A)完全能观测,(A,B)完全能控,则存在着最优反馈增益矩阵使得性能指标最小,有

K=R-1BTP。

(4)

其中:P为Riccati方程的唯一正定解。

3线性二次型最优控制的应用

对双关节机械手系统中的变量进行重新定义:

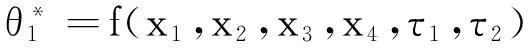
所以

其中:

在平衡点处进行线性化处理:

φ1=(m1lc1+m1l1)gcos θ1+

m2lc2gcos (θ1+θ2)=τ10;

φ2=m2lc2gcos (θ1+θ2)=τ20。

所以

4仿真验证

我们取

m1=1.900 8 kg；m2=0.717 5 kg；

l1=l2=0.2 m；lc1=0.185 22 m；

lc2=0.062 052 m；

I1=0.004 339 9 kg·m2；

I2=0.005 228 5 kg·m2。

每个关节选9个平衡点并进行线性化处理,i=1,2,…,9,且

(8)

式(8)转化到线性二次型最优控制中的矩阵形式为

我们让每一个关节的角度跟踪以下的参考轨迹,进而来检验该控制方法应用的跟踪能力和控制性能:

(9)

第二个关节角对参考轨迹θr2的响应曲线如图3所示。

根据响应曲线可以看出双关节机械手的关节角度对于其对应的参考轨迹具有非常快的响应能力以及非常强的跟踪能力。

为了进一步检测该控制方法的控制性能,我们让θ1、θ2跟随阶跃输入,观察双关节机械手关节角度的响应能力。第一个关节角对阶跃信号的响应曲线如图4所示。

第二个关节角对阶跃信号的响应曲线如图5所示。

仿真结果表明,θ1,θ2对于阶跃输入具有很好的跟踪能力且该系统能够迅速响应,大约0.13 s就能够达到稳定状态,具有响应速度快,跟踪能力高,控制性能好的优点。

5结语

首先对双关节机械手系统建立数学模型,为将线性二次型最优控制与双关节机械手系统有机结合,采用了在系统平衡点处进行线性化处理的方法,最后利用Matlab进行系统仿真。仿真发现,系统对给定的参考轨迹以及阶跃输入信号能够迅速响应。对于参考轨迹,第二个关节角几乎从一开始就能够实现完全跟踪；对于阶跃输入信号,两个关节角在大约0.13 s就能够实现完全跟踪。仿真表明这种控制策略具有很好的响应能力、跟踪能力以及控制性能。

参考文献:

[1]林瑞麟,郭新跃,蒋少茵.机器人的动态特性试验研究[J].华侨大学学报:自然科学版,1995,15(4):424-427.

[2]严学高.机器人原理[M].南京:东南大学出版社,1996.

[3]霍伟.机器人动力学与控制[M].北京:高等教育出版社,2005.

[4]程代展.非线性系统的几何理论[M].北京:科学出版社,1988.

[5]Tarn T J,Bejczy A K.Effect of Motor Dynamics on Nonlinear Feedback in Robot Arm Control,Proc[C]//23rd IEEE Conf.Robotics and Automation,1991.[6]Hisa T C.Adaptive Control of Robot of Manipulators[C]//A Review Proc of the IEEE Conf on Robotics and Automation,1986.[7]张福恩.状态反馈极点配置的直接方法[J].自动化学报,1986,12(2):162-167.

[8]赵广元.MATLAB与控制系统仿真实践[M].北京:北京航空航天大学出版社,2012.

[9]薛定宇,陈阳泉.基于MATLAB/Simulink的系统仿真技术与应用[M].北京:清华大学出版社,2002.

Application of Optimum Control of Linear Quadratic Type on Two-joint Manipulator

Liu Zhongdong,Lin Jiajia

(College of Automation and Electronic Engineering,Qingdao University of Science and Technology,Qingdao 266061,China)

Key wordsTwo-joint manipulator;Optimum control of linear quadratic type;Matlab

AbstractFirst,the thesis introduces math model systematically built by two-joint manipulator and linear processing conducted on the equilibrium point by the system.Then,the thesis introduces systematical controls to two-joint manipulator conducted by using optimum control strategies of linear quadratic type.At last,the thesis introduces control performance of the control system examined by using Matlab to conduct simulation.After step-input,the system can achieve full tracking in 0.13s.The simulation results indicate that it has good responsiveness and tracking ability.

doi:10.16468/j.cnki.issn1004-0366.2016.03.007.

收稿日期:2015-08-17;修回日期:2015-09-28.

作者简介:刘中冬(1962-),男,山东青岛人,教授,博士,研究方向为机电一体化、测量及自动控制技术.E-mail:269529351@qq.com.

中图分类号:TP241

文献标志码:A

文章编号:1004-0366(2016)03-0031-04

引用格式:Liu Zhongdong,Lin Jiajia.Application of Optimum Control of Linear Quadratic Type on Two-joint Manipulator[J].Journal of Gansu Sciences,2016,28(3):31-34.[刘中冬,林佳佳.线性二次型最优控制在双关节机械手中的应用[J].甘肃科学学报,2016,28(3):31-34.]