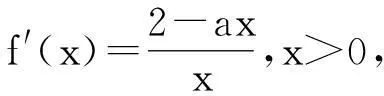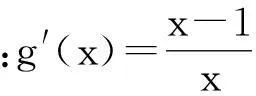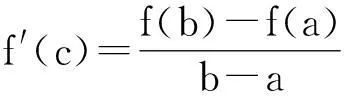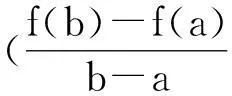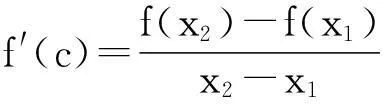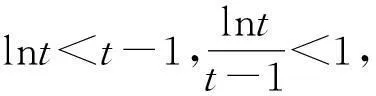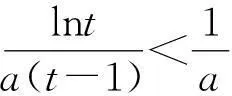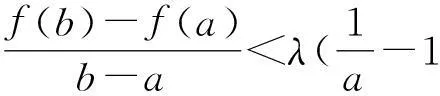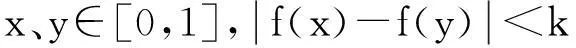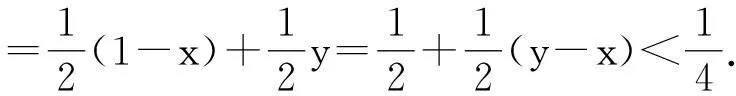由一道高三质检题看两类数学题的探究

云南省易门县第一中学　　吕顺宁　　(邮编：651100)



由一道高三质检题看两类数学题的探究

云南省易门县第一中学吕顺宁(邮编：651100)

2016年云南省玉溪市高中毕业生第一次教学质量检测理科数学第21题为：

题目已知函数f(x)=2lnx-ax+a,(a∈R).

(I) 讨论f(x)的单调性；

(II) 若∀x∈(0,+),f(x)≤0, 证明: 当0

这是一道构思精巧的函数与不等式的综合题，着重考查导数在研究函数的性质以及证明函数不等式中的综合运用，试题呈现起点低、落点高，知识综合性强，对考生能力要求高的特点. 考后分析知试题的第(II)问得分率非常低，可见该题实属不易.由此引发笔者对该问题解法分析和背景溯源以及由此引出的两类高考题解法探究的一些思考,赘述如下.

1试题原解答

(II) 证明由(I)知，若a≤0,f′(x)>0,f(x)在(0,+)上单调递增，又f(1)=0,故f(x)≤0不恒成立. 若a>2, 当时, f(x)单调递增, f(x)>f(1)=0,不合题意；若0f(1)=0,不合题意；若a=2,f(x)在(0,1)上单调递增, 在(1,+)单调递减, 符合题意，故a=2. f(x)=2lnx-2x+2且lnx≤x-1(当且仅当x=1时取“=”). 当0

上述解法由命题组提供. 不难看出, 证明的关键是通过过渡不等式：lnx≤x-1(当且仅当x=1时取“=”)的搭桥，将超越不等式放缩转化为代数不等式，从而使不等式获证.问题在于证明中不等式：“lnx≤x-1”的出现“像是从魔术师的帽子里跑出一只兔子”，显得突兀不自然, “解题应力求简单自然. 要抓住问题的实质，直接剖取核心，不要拖泥带水、兜圈子、使出很多‘费招’”[1]. 因此我们不禁要问:不等式“lnx≤x-1”是怎么想到的？而且能作为证题的关键依据？尽管我们老师知道课后习题：“ex>x+1,x≠0”这一结论(见人教A版选修2—2第32页B组第1题第(3)小题)，对它两边取自然对数,再用x-1替换x即可得到.但不至于又要求学生将其作为重要结论加以记忆，日后用之吧？再者，在高考复习备考中面对学生，面对该题，就用上述证法讲解吗？“以学生的思维为起点，追求自然合理的解法”当是解题教学的重点,而且,“在解题过程中，通过分析、思考引领学生去体味论证逻辑的严谨与合情推理的豁达, 这是数学教学不可缺失的培养学生直观感性认识与理性思维逻辑的重要途径”. 所以，有必要对该题的证法进行探索.

2试题的另证

点评很多时候，我们的确纠结于“问题何解？”而忽视了对“如何解题的思考”？回顾上述另解的过程，不难看出：证明的思维切入点是利用式子的结构特征构造函数，将证明不等式的问题转化为研究新函数的单调性而已. 式子的结构特征如何发现？著名数学家，数学教育家波利亚早就指出：“如果不变化问题，我们几乎不能有什么进展”；而单墫教授也说：“不断地变更问题, 直到它变得易于解决(最好化成一个你所熟悉的问题), 这是解题的常用方法. 从理解题意时，我们就开始这样做”[1].

3试题的背景揭示及在该背景下的相关高考题的另解

根据拉格朗日中值定理，再回到原题. 显然函数f(x)=2lnx-2x+2(x>0)满足:

事实上, 好多高考题或模拟题的压轴题都有高等数学的背景,不仅研究怎样解同时还注意研究试题的背景来源, 弄清了这些问题，则更有利于认识问题的本质.

例1已知函数f(x)=lnx-mx+m,m∈R.

(1)已知函数f(x)的图象在点(1,f(1))处与x轴相切，求实数m的值；

(2)求函数f(x)的单调区间；

现摘录原解答如下：

因为01), 则

结论 已知函数f(x)=λ(lnx-x-1), (λ>0), 对于任意的0

例2 (2014年高考辽宁卷理12题)已知定义在[0,1]上的函数f(x)满足：

①f(0)=f(1)=0;

解现摘录原解答如下：

点评本题主要考察绝对值不等式、分类讨论思想，意在考查考生对数学思想方法的应用能力. 但是, 上述解法中对x-y的分类讨论，其标准的确定是思考的难点. 事实上，容易看出题设中定义在[0,1]上的抽象函数f(x)满足洛尔定理的三个条件, 若要回避分类讨论，结合选择题的解题特点，可构造定义在[0,1]上的函数f(x)=x2-x,再利用熟知的重要结论:

4不等式: “lnx≤x-1”的再认识及其变式应用

先证明该不等式成立.

如果用x+1替换不等式lnx≤x-1中的x得:ln(x+1)≤x;用x+2替换不等式lnx≤x-1中的x得:ln(x+2)≤x+1.

下面用这两个不等式巧解几道高考题.

(I) 求a,b的值；

例4(2013 年高考新课标全国II卷理21题)已知函数f(x)=ex-ln(x+m).

(I) 设x=0是f(x)的极值点, 求m, 并讨论f(x)的单调性；

(II) 当m≤2时, 证明:f(x)>0.

根据不等式ln(x+2)≤x+1, 则只需证明：ex-ln(x+2)≥ex-x-1,即ex-x-1≥0成立即可.

令g(x)=ex-x-1, 则g′(x)=ex-1, 当x∈(0,+)时，g′(x)>0, 当x∈(-2,0)时，g′(x)<0, 所以函数g(x)在(-2,0)上单调递减，在(0,+)上单调递增，在x=0处取得最小值：g(x)min=g(0)=0, 故原不等式获证.

通过以上对质检题的解法的分析、背景的解读和结论的引申, 不仅挖掘了试题的源与流,而且发现了与质检题分别有相同高数背景,并探讨了它们不同于标准解答的解法.同时可将上述探究过程设计成研究性学习的教学案例.

参考文献

1单墫. 解题研究. 南京：南京师范大学出版社

2刘玉链, 傅沛仁. 数学分析讲义.北京：高等教育出版社

3郑廷楷. 名师解题(四川卷).(金考卷)2015年全国各省市高考试题汇编(第一期，数(理科)). 乌鲁木齐：新疆青少年出版社

4袁义东, 汪仁林. 2015年高考数学模拟试题(2) . 数理天地(高中版). 2015(2)

5王金泽. 名师解题(辽宁卷).(金考卷)2014年全国各省市高考试题汇编(第一期, 数学(理科)). 乌鲁木齐：新疆青少年出版社

(收稿日期：2016-02-24)