涉及三角形高与中线的欧拉不等式的加强

四川成都实验外国语学校　　宿晓阳　　(邮编：611731)



涉及三角形高与中线的欧拉不等式的加强

四川成都实验外国语学校宿晓阳(邮编：611731)

众所周知,著名的欧拉不等式为： 设ΔABC外接圆和内切园的半径分别为R,r，则R≥2r.

安振平先生在文中提出如下一个优美的不等式

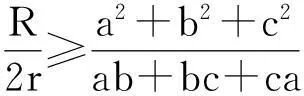
本文将给出类似于上式且涉及三角形高，中线的欧拉不等式的加强.供参考与欣赏.

命题1设ΔABC的三边为a,b,c上的高分别为ha,hb,hc.外接圆和内切圆的半径分别为R,r，则

①

证明设ΔABC面积为△，半周长为s,则由三角形的面积公式

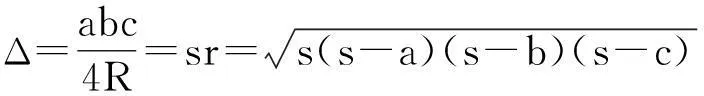
易知(①)式等价于

②

又a2≥a2-(b-c)2=4(s-b)(s-c)，

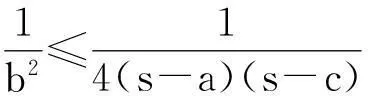
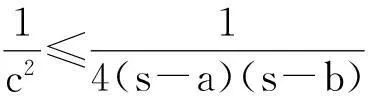
三式相加，即得②式.故①式成立.

命题2设ΔABC的三边为a,b,c上的中线分别为ma,mb,mc.外接圆和内切圆的半径分别为R,r，则

③

证明由三角形中线公式，知

再注意到三角形恒等式及文中的不等式：

a2+b2+c2=2(s2-4Rr-r2)

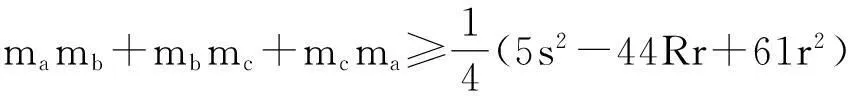
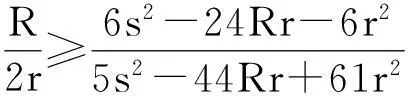
(5R-12r)(16Rr-5r2)≥44R2r-109Rr-12r3

④

当5R-12r>0时，由著名的Gerrestsen不等式得s2≥16Rr-5r2，欲证式④，即证④⟺(R-2r)(R-r)≥0.

由著名的Euler不等式R≥2r,即知成立.

当5R-12r=0时，④式显然成立.

当5R-12r<0时，由著名的Gerrestsen不等式得s2≤4R2+4Rr+3r2.

欲证式④，即证④⟺(5R-3r)(R-2r)(R-r)≥0.

由著名的Euler不等式R≥2r.即知④式成立.

参考文献

1安振平.外森比克不等式的再探究.中学数学教学,2015(2)

2褚小光，杨学枝.关于三角形中线的若干不等式，不等式研究.拉萨：西藏人民出版社,2000(6)

(收稿日期：2016-04-06)