不同压缩比 Sierpinski 垫的 Hausdorff 测度和维数
晋 娜, 魏毅强
(太原理工大学 数学学院, 山西 太原 030024)
不同压缩比 Sierpinski 垫的 Hausdorff 测度和维数
晋娜, 魏毅强
(太原理工大学 数学学院, 山西 太原 030024)
摘要:系统讨论了改变压缩比c时 Sierpinski-垫片的 Hausdorff 维数与测度的变化. 对于不同范围的c分别运用不同的方法讨论了它们的 Hausdorff 测度与维数. 压缩比时, 通过投影与构造质量分布, 将计算康托集测度的过程与计算 Sierpinski-垫测度的过程结合起来, 计算出此时S的测度的具体值, 并且该值为 1. 当压缩比在到之间时, 首次系统讨论了此时S的重叠结构问题, 得到了S具有完全重叠结构时c的取值. 同时,S不具有重叠结构时, 有S的维数具体值为.
关键词:压缩比; Sierpinski-垫; Hausdorff 维数与测度
在分形中, 测度与维数的估计和计算是十分重要也是非常困难的, 目前为止, 除了少数特殊分形的测度与维数被计算出来外(如均匀康托集[1]), 大部分分形的测度与维数的计算仍然是需要解决的难题, 尤其是对于满足开集条件的自相似集, 它们的Hausdorff维数与它的自相似维数相等, 但是对于它们测度的计算却没有行之有效的方法. 很多文献都对此做过有益讨论[2-15], 尤其是作为三个经典自相似集之一的Sierpinski-垫片, 很多文献对于它的测度进行了研究[8-15], 尤其是文献[8], [10]和[11]给出了目前测度最好的上下界以及计算机的实现程序.
1基本构造与命题
在 Euclid 平面R2上取一个单位正三角形, 记作 S0. 对 S0做压缩映射 f1, f2, f3, 即对 S0中的任意点(x,y), 令

上述过程无限进行下去, 得到

定义 1[16](开集条件)设 S1,S2,…,Sm是 {D⊂Rn} 的压缩映射, 使
对每个 i,ci<1, 如果存在非空的有界开集 V 使得对于不交的并
则称Si满足开集条件.

定义 3[17]设 I0=[0,1], Ω={0,1,2}. 对 δ∈Ωk, 记 δ=δ(1)…δ(k), 其中 δ(i)∈Ω, 1 ≤ i ≤ k. 令
记 Iδ为 Eλ,k的基本区间, 即 Iδ=Sδ(1)Sδ(2)… Sδ(k)(I0), 设 k≥1, 如果存在 δ, τ∈Ωk, δ≠τ, 使得 Iδ=Iτ, 则称 Eλ具有完全重叠, 否则 Eλ不完全重叠.
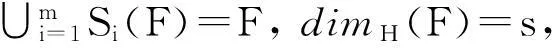

引理 3[17]Ek满足开集条件, 当且仅当Ek不具有完全重叠时.
2主要结论

下面证明 Hs(S)=1. 显然 Hs(S)≤1, 只需取 {S0} 为它的一个覆盖即可. 因此只要证明 Hs(S)≥1 即可.

在 E 上分配一个质量分布 μ, 使 μ(I)=|I |s. 以单位质量从 E0=[0,1]开始, 平分质量到E1的每个基本区间上, 如此下去, 得到如下的质量分布
可以证明:如果 U 为 E 上的任一覆盖, 则有 μ(U)≤|U|s.
事实上, 先估计端点在 E 上任一区间 U 的质量 μ(U), 设I为包含U的最小基本区间, 且设 I 为 Ek的一个基本区间. 如果 U 刚好与 I 重合, 显然此时 μ(U)=|U|s.如果 U 包含在 I 的内部, 又因 U 的端点在 E 上, 则存在一个 r, 使 U 刚好包含 Ek+r的整数 n 个基本区间 Ir+k, 此时 μ(U)=n| Ir+k|s≤|n|Ir+k|+(n-1)|I'||s=|U|s(其中I'为 Ek+r中基本区间的较小的间隔), 因此不等式对端点在 E 上的任一区间 U 都成立. 对端点不在 E 上的任一区间 U, 只需要将上述分析应用到包含 U∩F 的最小区间上, 有 μ(U)=μ(U∩F)≤|U∩F|s≤|U|s.
下面将属于 Ek的每个基本区间 I 上的质量均匀分布在它对应的 Sk的基本三角形Δi1i2…ik上, 即相当于在 S 上分配一个质量分布


此时, S 是否具有完全重叠可由 c 是否是方程 cn=bij的解给出, 有如下结论:




至此, 我们可以将图3看做一个基本图形, 即两个正三角形边长均为 c, 相交的小正三角形的边长为 2c-1, 那么我们可以得到一系列重叠的正三角形Δ2cn-(2c-1),Δcn(2c-1)以及Δcn+c-1. 而每两个相交三角形我们均可以看作是基本图形改变两个大的正三角形的边长以及中间相交的小的正三角形的边长所得到的.

参考文献:
[1] Falconer K J. The geometry of fractal sets[M]. Cambridge university press, 1985.
[2] 文胜友, 许绍元. 关于自相似集的 Hausdorff 测度[J]. 数学学报,2001, 44(1): 117-124.
Wen Shengyou, Xu Shaoyuan. On hausdorff measures of self-similar sets[J]. Acta Mathematica Sinica, 2001, 44(1): 117-124. (in Chinese)
[3] Jia Baoguo. Bounds of the Hausdorff measure of the Koch curve[J]. Applied Mathematics and Computation, 2007(190): 559-565.
[4] 许绍元,徐望斌. 关于自相似集的上凸密度与上球密度研究的若干进展[J]. 赣南师范学院学报, 2012(3): 1-3.
Xu Shaoyuan, Xu Wangbin. Some latest advances in upper convex density and upper sphere density[J]. Journal of Gannan Normal University, 2012(3): 1-3. (in Chinese)
[5] Rao Hui, Wen Zhiying. A class of self-similar fractals with overlap structure[J]. Advances in Applied Mathematics, 1998(20): 50-72.
[6] Zou Yuru, Yao Yuanyuan, Li Wenxia. A class of Sierpinski carpets with overlaps[J]. Math. Anal. Appl., 2008(340): 1422-1432.
[7] 邓启荣, John HARDING, 胡天佑. 有重叠的自相似集的 Hausdorff 维数[J]. 中国科学(A辑),2008, 38(6): 631-640.
Deng Qirong, John HARDING, Hu Tianyou. Hausdorff dimensions of self-similar sets with overlapping structure[J]. Sci. China A, 2008, 38(6): 631-640. (in Chinese)
[8] 周作领. Sierpinski 垫片的 Hausdorff 测度[J]. 中国科学(A辑),1997, 40(6): 491-496.
Zhou Zuoling. Hausdorff measures of Sierpinski gasket[J]. Sci. China A. 1997, 40(6): 491-496. (in Chinese)
[9] 何伟弘, 周作领. 上凸密度函数与Hausdorff测度-Sierpinski垫片[J].中山大学学报(自然科学版), 2001, 40(1): 112-113.
He Weihong, Zhou Zuoling. Upper convex density and Hausdorff measure of the Sierpinski gasket[J]. Acta Scientiarum Naturalium Universitatis Sunyatseni, 2001, 40(1): 112-113. (in Chinese)
[10] Jia Baoguo. Bounds of Hausdorff measure of the Sierpinski gasket[J]. J.Math. Anal. Appl., 2007(330): 1016-1024.
[11] Peter Mora. Estimate of the Hausdorff measure of the Sierpinski triangle[J]. World Scientific Publishing Company Fractals, 2009, 17(2): 137-148.
[12] Sun Shanhui, Xu Shaoyuan. On an algorithm of the upper estimation of the Hausdorff measure of a class of Sierpinski gaskets[J]. Journal of Huaibei Goal Inductry Teachers College(Natural Science), 2010, 31(3): 6-9.
[13] 王谦, 何国龙. 关于 Sierpinski 垫片的 Hausdorff 测度的上界估计[J]. 浙江师范大学学报(自然科学版), 2010, 33(4): 392-397.
Wang Qian, He Guolong. Upper estimate of Hausdorff measure of the Sierpinski gasket[J]. Journal of Zhejiang Normal University (Natural Science), 2010, 33(4): 392-397. (in Chinese)
[14] 刘春苔. 一类特殊广义Sierpinski-垫片的Hausdorff维数[J]. 武汉工业学院学报, 2011, 30(3): 110-112.
Liu Chuntai. Hausdorff dimension of a generalized Sierpinski gasket[J]. Journal of Wuhan Polytechnic University, 2011, 30(3): 110-112. (in Chinese)
[15] Zhang Yunxiu, Gu Hui. Estimation of the Hausdorff measure of a kind of Sierpinski carpet[J]. Chin Quart of Math., 2012, 27(1): 59-62.
[16] Falconer K J. Fractal Geometry-Mathematical Foundations and Applications[M]. New York: Wiley, 1990.
[17] 文志英. 分形几何的数学基础[M]. 上海: 上海科技教育出版社, 2000.
Hausdorff Measures and Dimensions of Sierpinski Gaskets with Different Compression Ratios
JIN Na, WEI Yi-qiang
(Department of Mathematics, Taiyuan University of Technology, Taiyuan 030024, China)
Key words:compression ratio; Sierpinski gasket; Hausdorff measure and dimension
Abstract:This paper discussed systematically the change of Hausdorff dimensions and measures of the Sierpinski-gaskets when the compression ratio was changed. For the different range ofc, the paper researched their Hausdorff dimensions and measures by using corresponding methods. While the compression ratio was less than, through the projection and structural mass distribution, the calculations of Cantor set measure and Sierpinski gaskets were combined, then the paper had the specific value of their measures, and this value was 1. Whilecwas more thanand less than, the paper discussed overlapping structure problem ofSat the first time and the value ofcwhileSwas completely overlapped was received. At the same time, Hausdorff dimension waswhileShadn’t completely overlapping structure.
文章编号:1673-3193(2016)03-0229-05
收稿日期:2015-10-18
作者简介:晋娜(1989-), 女, 硕士生, 主要从事分形几何与动力系统研究.
通讯作者:魏毅强(1961-), 男, 教授, 主要从事分形几何和动力系统研究.
中图分类号:O143
文献标识码:A
doi:10.3969/j.issn.1673-3193.2016.03.005

