关于四元数体上某类矩阵方程的极小范数最小二乘解

张晋芳， 杨　晋， 任艳萍

(太原理工大学 数学学院， 山西 太原 030024)



关于四元数体上某类矩阵方程的极小范数最小二乘解

张晋芳， 杨晋， 任艳萍

(太原理工大学 数学学院， 山西 太原 030024)

摘要:对四元数体上某类自共轭矩阵方程， 在两两可交换的前提下， 研究了矩阵方程的极小 Frobenius 范数最小二乘解. 同时， 在有解条件下给出了通解的表达形式．利用四元数体上自共轭矩阵奇异值分解的充分必要条件， 运用四元数体上 Frobenius 范数正交矩阵乘积不变性， 讨论了某类矩阵方程的最小二乘解， 给出了极小 Frobenius 范数最小二乘解及其通解的表达形式， 进而推广到了更为一般的矩阵方程.

关键词:四元数体； 矩阵方程； 奇异值分解； 最小二乘解； 极小范数

0引言

近 40 多年来， 矩阵方程的研究方兴未艾， 对它们的研究除了在理论上有重要意义外， 还对力学、 控制论、 理论物理、 理论电工技术、 遥感技术等各种领域有重要作用．考虑到四元数和四元数矩阵的广泛应用， 对四元数矩阵方程理论及数值计算的研究就显得尤为重要， 其中四元数矩阵的奇异值分解是核心内容. 如文献[1]给出了四元数矩阵上的奇异值分解. 文献[2-6]利用四元数矩阵的奇异值分解得到了一些结论.

1预备知识

用 Ω 表示四元数体； Ωm×n表示全体m×n四元数矩阵的集合； Sn(Ω) 表示四元数体 Ω 上全体 n×n 自共轭矩阵的集合； SSn(Ω) 表示四元数体 Ω 上全体 n×n 反自共轭矩阵的集合； UΩn×n表示四元数酉矩阵的集合； ‖·‖ 表示矩阵的 Frobenius 范数， 且这里的“范数”指的是矩阵 Frobenius 范数.

文献[7-9] 研究了各类矩阵方程的极小范数最小二乘解， 文献[6]利用四元数矩阵的奇异值分解得到了 AX+XB+CXD=F 的极小范数最小二乘解， 及其有解条件下的 Hermite 最小二乘解与其通解的表达形式. 作为对该方程形式的拓广旨在解决下面问题.

问题 1

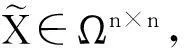
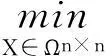
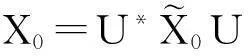
问题 2

求 X0为矩阵方程

AXB+CXD+FX=H

的极小 Frobenius 范数最小二乘解.

问题 3

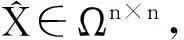
2引理及其主要结论

引理[10]Ai∈SCn(Ω)(i=1,2,…,t)， 则存在 U∈UΩn×n将 UAiU*同时化为实对角矩阵的充分必要条件为 ApAq=AqAp(p,q=1,2,…,t).

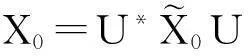
证明由引理可知， 存在 U∈UΩn×n， 使得

式中： ai， bi， ci， di, ei(i=1,2,…,n) 分别是 A， B， C， D， E 的全部特征值. 于是

‖AXB+CXD+XE-H‖2=

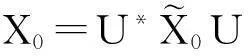
证明由于 ‖AH‖=‖A‖， 本质上问题2 和问题1是一样的， 所以由定理 1 直接可以得出定理2的结果.

证明由引理可知， 存在 U∈UΩn×n， 使得

参考文献:

[1] 邓勇， 黄敬频， 杜刚. 四元数体上一类矩阵方程的极小范数最小二乘解[J]. 纯粹数学与应用数学， 2010， 26(2)： 191-192.

Deng Yong， Huang Jingpin， Du Gang. The minimal norm and least square solution to a class of matrix equations in the quaternion field[J]. Pure and Applied Mathematics， 2010， 26(2)： 191-192. (in Chinese)

[2] Shifang Yuan， Anping Liao， Yuan Lei. Least squares Hermitian solution of the matrix equation with the least norm over the skew field of quaternions[J]. Mathematical and Computer Modelling， 2008， 48： 1-100. (in Chinese)

[3] 王卿文， 薛有才. 体与环上的矩阵方程[M]. 北京： 知识出版社， 1996.

[4] 王开明， 刘永辉. 四元数矩阵方程的最小二乘解[J]. 洛阳大学学报， 2004， 19(2)： 1-4.

Wang Kaiming， Liu Yonghui. The Hermitian Least-square Solution of the Quaternion Matrix Equation[J]. Journal of LuoYang university， 2004， 19(2)： 1-4. (in Chinese)

[5] 刘永辉. 四元数矩阵方程的最小二乘解[J]. 数学研究， 2003， 36(2)： 145-150.

Liu Yonghui. The Least square Solutions to the Quaternion matrix Equation[J]. Journal of Mathematical Study， 2003， 36(2)： 145-150. (in Chinese)

[6] 韦刚和. 关于四元数体上矩阵对角化的几个定理[J]. 常熟理工学院学报(自然科学版)， 2012， 26(10)： 37-40.

Wei Ganghe. Several Matrix Diagonalization Theorems on the Quaternion[J]. Journal of Changshu Institute Technology(Natural Sciences). 2012， 26(10)： 37-40. (in Chinese)

[7] Loring T A. Factorization of matrices of quaternions[J]. Expo.Math， 2012， 33(15)： 1-21.

[8] 尤兴华， 马圣容. 李亚普诺夫方程的简洁解及其应用[J]. 南京师范大学报(自然科学版)， 2011， 3(1)： 44-49.

You Xinghua， Ma Shengrong. The Simple Formulae of Solutions to Liapunov Matrix Equation and Its Application[J]. Journal of Nanjing Normal University(Natural Science Edition)， 2011， 3(1)： 44-49. (in Chinese)

[9] 尤兴华， 马圣容. 关于矩阵方程组的最小二乘解和极小范数最小二乘解[J]. 苏州大学(自然科学版)， 2012， 4(1)： 23-27.

You Xinghua， Ma Shengrong. Least squares solution and minimum-norm least-squares solution of matrix equations [J]. Journal of Soochow University(Natural Science Edition)， 2012， 4(1)： 23-27. (in Chinese)

[10] 庄瓦金. 关于四元数矩阵的奇异值分解[J]. 新疆大学学报， 1987， 4(1)： 22-28.

Zhuang Wajin. On the singular value decomposition for quaternion matrices[J]. Journal of Xinjiang University (Natural Science Edition)， 1987， 4(1)： 22-28. (in Chinese)

The Minimum Norm and Least Square Solution to a Class of Matrix Equations in the Quaternion Field

ZHANG Jin-fang, YANG Jin， REN Yan-ping

(School of Mathematics, Taiyuan University of Technology, Taiyuan 030024, China)

Key words:quaternion field; matrix equation; singular value decomposition; the least square solution; the minimum norm

Abstract:For certain types self-conjugate matrix equation on quaternion field, we studied the minimal Frobenius norm least square solution of matrix equation under the premise of exchangeable, and gave the solution of general solution form under the condition of the solvability. By using sufficient and necessary conditions of the self-conjugate matrix singular value decomposition on quaternions, and invariance of Frobenius norm of orthogonal matrix product on quaternion, we discussed the least-square solutions of a kind of matrix equation, and give the expression of general solution form of the minimal Frobenius norm least squares solution, and extend to the more general matix equation in further.

文章编号:1673-3193(2016)03-0225-04

收稿日期:2015-10-30

作者简介：张晋芳(1989-)， 女， 硕士生， 主要从事应用数学等研究.

中图分类号:O151.21

文献标识码:A

doi:10.3969/j.issn.1673-3193.2016.03.004