基于非线性控制算法的弹性电磁驱动器的建模

赵海军，李明东，岳　 淼，罗　宇

(西华师范大学 计算机学院，四川 南充　637009)

基于非线性控制算法的弹性电磁驱动器的建模

赵海军，李明东，岳 淼，罗宇

(西华师范大学 计算机学院，四川 南充637009)

摘要：提出了一种弹性电磁驱动器系统及其数学模型。首先是建立起单面电磁驱动器的动态数学模型，并对具有二次非线性输入的系统提出了一种非线性控制算法来确保系统的稳定性和对有界扰动的抑制；其次，在对单面弹性电磁驱动器研究的基础上，又构建出了双面弹性电磁驱动器，并提出了一种非线性控制算法；最后通过数值仿真对双面弹性电磁驱动器的非线性控制进行了验证。仿真结果表明，算法不仅能够获得预期的性能，同时也能确保电磁极板不会吸合在一起。

关键词：弹性；电磁驱动；非线性；建模；扰动抑制

0引言

随着微型加工和微纳米制造技术的快速发展，高性能微电机系统和纳米电机系统将广泛用于纳米计算机、医药、生物技术及其他工业应用领域，如采用微光电机系统的光网络设备[1,2]、采用加速计和陀螺传感器的汽车自适应牵引和滑移控制[3,4]、微型电磁驱动器和硬盘磁头的精确控制[5-8]等。

众所周知，一个由电压驱动的平行板有一个标称间隙三分之一的稳定驱动范围，超过这个位移时，静电力就成为主要的悬浮恢复力，电极就会吸合从而导致断裂。因此，基于线性化模型的线性控制器在大扰度时是不稳定的[9]。

对于电磁驱动器的研究已见诸不少文献。文献[10]采用多线圈多磁极结构设计出了一种新型MEMS摆动式微电磁驱动器；文献[11]提出了一种蕴含磁双稳机制，易于集成化和模块化的新型微电磁驱动器，由镍弹性平台、中央垫片、平面线圈三部分构成；文献[12]针对电磁驱动器的定位和跟踪问题，提出了一种新的控制律技术，该技术基于循环自适应电流预作用和滑动面，由磁力来补偿弹性力，从而使软着陆点的速度达到最小；文献[13] 采用一个隔膜、微线圈和一个磁铁设计出了一种微型电磁驱动器，由施加到微线圈的电流和磁铁之间产生的电磁力，引起膜片偏转，从而控制驱动调节。

目前，上述文献中提到的大多数弹性电磁驱动器都存在驱动电压过高、驱动力矩和行程过大，响应速度慢且动态响应时间过长，这些缺点都会导致外界扰动的抑制功能降低。基于此，本文提出了由单面和双面电磁力驱动的弹性电磁驱动系统及其数学模型。我们首先建立起单面电磁驱动器的动态数学模型，并研究了在具有未知常数扰动和二次非线性输入情况下的非线性控制算法，构建出了一个非线性控制器来保证这种情况下的稳定性和对未知扰动的抑制；其次，在对单面弹性电磁驱动器研究的基础上，又构建出了双面弹性电磁驱动器，并提出了一种非线性控制算法，算法不但能够确保任何时候电磁平板不吸合在一起，而且获得了预期的控制性能；最后通过数值仿真对双面弹性电磁驱动器的非线性控制进行了验证。仿真结果表明，本文提出的非线性弹性电磁驱动器是稳定的，具有可靠的扰动抑制性能。

1单面弹性电磁驱动器的动态模型

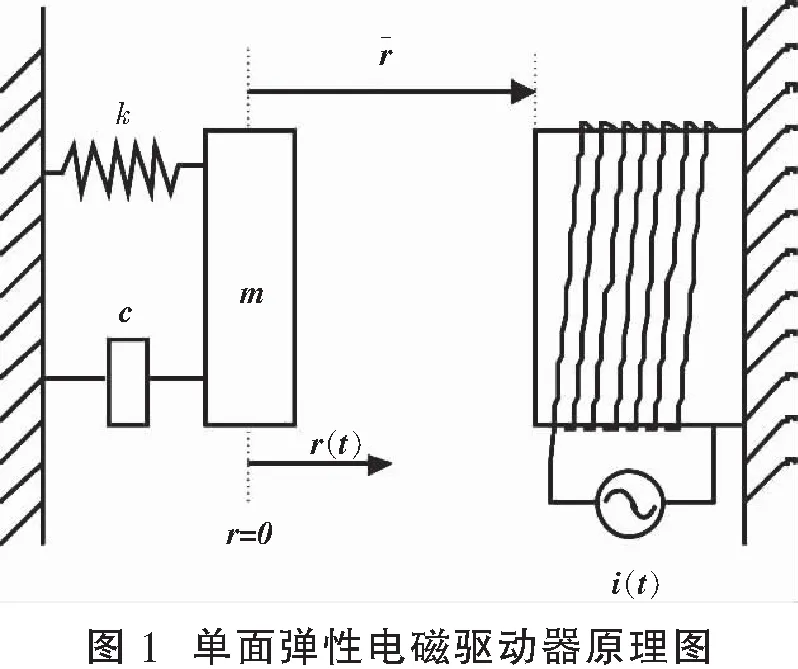
本文提出的单面弹性电磁驱动器原理图如图1所示，其动力学方程由下式给出：

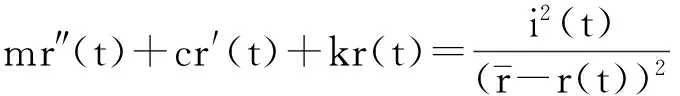
(1)

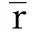
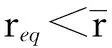
(2)

式中ieq为使振荡器位置保持在r=req时需要的电流。为了把平衡点req变换到一个新坐标系的原点，令ξ(t)=r(t)-req’，则方程(1)就可以用状态空间形式写为：

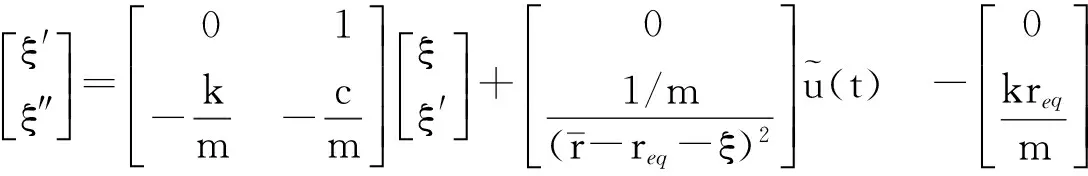
(3)

(4)

系统从稳定过渡到不稳定也可以通过位函数来理解。总的位函数VPE可以用无量纲形式写为：

(5)

2单面弹性电磁驱动器的非线性控制

为了实现单面弹性电磁驱动器的非线性控制，我们考虑具有二次非线性输入的情况，并考虑单输入单输出系统

(6)

具有标量控制输入u(t)∈R，标量输出y(t)∈R，对于t≥0，有界扰动d(t)∈R且满足d(t)≤0。假设(A，B，C)为最小正实数，考虑控制器：

(7)

3双面弹性电磁驱动器及其控制算法

根据前面提出的单面弹性电磁驱动器模型，我们构建的双面弹性电磁驱动器如图2所示。对于图2所示系统来说，其动力学方程为：

(8)

式中m为振荡器质量，c为阻尼常数，k为弹性常数，i1(t)和i2(t)为电磁铁电流，γ1和γ2为每个电磁铁对应的常数，且α1=γ1m，α2=γ2m，fd(t)为有界外力扰动，且对于t≥0，存在α3>0且|fd(t)|<α3。

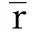
(9)

并设控制输入i1(t)和i2(t)由下式给出：

(10)

式中

(11)

且

(12)

采用式(10)—(12)，式(8)变为：

(13)

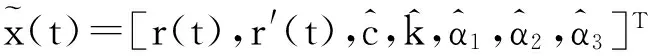
(14)

式中x(t)=[r(t)r′(t)]T，且V0(r(t))由下式定义：

(15)

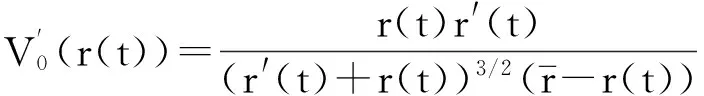
(16)

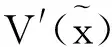
(17)

4算法性能的数值仿真

首先，仿真算法对一个方波fd(t)扰动的干扰抑制，方波fd(t)的周期为0.16s，得到的仿真结果如图3所示。从图3可见，本文提出的控制算法能够抑制时变干扰并能保证振荡器和电磁铁不吸合在一起。

其次，对振荡器稳定时靠近右边电磁铁的req=1.99进行了仿真验证。对此，给振荡器一个朝右边电磁铁的初始“推动”来得到初始条件(r(0),r′(0))=(0.0,50.0)，这时得到的仿真结果如图4所示。从图4可见，控制算法能够使系统稳定在r =1.99。

5结论

本文构建了一种单/双面弹性电磁驱动器系统及其数学模型，并对具有二次非线性输入的系统提出了一种非线性控制算法来确保系统的稳定性和对有界扰动的抑制。仿真表明，算法不仅能够获得预期的性能，同时也能确保电磁板不会吸合在一起。

参考文献：

[1]BIFANOTG,PERREAULTJ,MALIRK,etal.Microelectromechanicaldeformablemirrors[J].IEEEJournalofSelectedTopicsinQuantumElectronics,1999, 5(1):83-89.

[2]LINLY,GOLDSTEINEL,TKACHRW.Free-spacemicromachinedopticalswitchesforopticalnetworking[J].IEEEJournalofSelectedTopicsinQuantumElectronics,1999,5(1):4-9.

[3]ELWENSPOEKM,WIEGERINKR.Mechanicalmicrosensors[M].Berlin：Springer, 2001.

[4]YAZDIN,NAJAIIK.Anall-siliconsinglewafermicro-gaccelerometerwithacombinedsurfaceandbulkmicromachiningprocess[J].JournalofMicroelectromechanicalSystems, 2000, 9(4):544-550.

[5]FANLS,OTTESENHH,REILYTC,etal.Magneticrecording-headpositioningatveryhightrackdensitiesusingamicroactuator-based,two-stageservosystem[J].IEEETransactionsonIndustrialElectronics,1995,42(3):222-233.

[6]HORSLEYDA,SINGHA,HOROWITZR,etal.Angularmicropositionerfordiskdrives[C]//ProceedingsoftheIEEEMEMS’97Workshop,Nagoya,Japan:IEEE,1997：454-459.

[7]HORSLEYDA,WONGKOMETN,HOROWITZR,etal.Precisionpositioningssingamicrofabricatedelectrostaticactuator[J].IEEETransactionsonMagnetics,1999,35(2):993-999.

[8]IMAMURAT,KOSHIKAWAT,KATAYAMAM.TransversemodeelectrostaticeicroactuatorforMEMS-basedHDDslider[C]//ProceedingsofNinthInternationalWorkshoponMicroElectromechanicalSystems,SanDiego,America:IEEE,1996:216-221.

[9]LYSHEVSKISE,LYSHEVSKIMA.Analysis,dynamicsandcontrolofmicro-electromechanicalsystems[C]//Proceedingsofthe2000AmericanControlConference,Chicago,IL,America:IEEE, 2000,5: 3091-3095.

[10]贾书海,李以贵,杨春生,等.新型MEMS摆动式微电磁驱动器研制[J].中国机械工程,14(12):1004-1007.

[11]张晓鹏,戴旭涵,苗小丹,等.一种新型MEMS双稳态微电磁驱动器的研究[J].传感器与微系统,2009, 28(6):117-120.

[12]MERCORELLI,PAOLO.Anantisaturatingadaptivepreactionandaslidesurfacetoachievesoftlandingcontrolforelectromagneticactuators[J].IEEE/ASMETransactionsonMechatronics,2012,17(1):76-85.

[13]LEECY,CHENZH,CHANGHT,etal.Designandfabricationofanovelmicroelectromagneticactuator[C]//SymposiumonDesign,Test,IntegrationandPackagingofMEMS/MOEMS,Nice,France:IEEE, 2008:52-55.

ModelingofElasticElectromagneticActuatorBasedonNonlinearControlledAlgorithm

ZHAOHaijun，LIMingdong，YUEMiao，LUOYu

(SchoolofComputer,ChinaWestNormalUniversity,NanchongSichuan637009,China)

Abstract:An elastic electromagnetic actuator system and its mathematical model are presented in this paper.Firstly,the dynamic mathematical model of single-sided electromagnetic actuator is established and a nonlinear controlled algorithm with quadratic input nonlinearity is presented to ensure the stability of the system and to inhibit the bounded disturbances.Secondly,based on the study of single-sided elastic electromagnetic actuator,a double-sided elastic electromagnetic actuator is constructed as well and a nonlinear controlled algorithm put forward.Finally,the numerical simulation on the nonlinear controlling of double-sided elastic electromagnetic actuator is verified.The simulation results show that the algorithm proposed can not only obtain expected performance,but also can ensure that electromagnetic plate will not be pulled together.

Keywords：elasticity;electromagnetic actuating;nonlinearity;modeling;disturbance suppression

文章编号：1673-5072(2016)02-0237-06

收稿日期：2015-04-23

基金项目：西华师范大学基本科研业务费专项资金资助项目(14C002)

作者简介：赵海军(1966—)，男，四川广安人，教授，主要从事通信方面的教学及科研。 通讯作者：赵海军，E-mail:zhaohai_jun@163.com

中图分类号：O441.4

文献标识码：A

DOI：10.16246/j.issn.1673-5072.2016.02.023