多跨鞍形膜结构风荷载的数值模拟研究

张建胜，陶　瑾，王建东，李伟杭，吴力平

(1.浙江工业大学 建筑工程学院，浙江 杭州310014；2.杭州科技职业技术学院 城市建设学院，浙江 杭州 310012)

多跨鞍形膜结构风荷载的数值模拟研究

张建胜1，陶瑾1，王建东1，李伟杭1，吴力平2

(1.浙江工业大学 建筑工程学院，浙江 杭州310014；2.杭州科技职业技术学院 城市建设学院，浙江 杭州 310012)

摘要：多跨鞍形膜结构是工程中常用的一种大跨空间结构形式，风荷载是其结构设计的控制性因素.采用CFD数值模拟方法研究其平均风荷载特性，分析膜面初始预张力、来流风向角和矢跨比对多跨鞍形膜结构表面的风压分布特性的影响规律.结果表明：膜面初始预张力的大小主要影响膜面所受正风压区域的大小，膜面初始预张力越大，受正压区域越大.来流风向角会改变膜面正负极值风压的分布，正负极值一般出现在与风向角垂直的边缘处.不同的矢跨比会产生不同大小的膜面风压系数，但是从总体上看风压的分布形式是相同的.

关键词：多跨鞍形膜结构；CFD数值模拟；风压分布；影响规律

膜结构是20世纪中期发展起来的一种新型建筑结构形式，膜结构建筑是21世纪最具代表性与充满前途的建筑形式，从其产生至今已经应用到我国的许多建筑中[1].膜结构属于风敏感性结构[2]，又称为柔性结构[3]，与传统的钢筋混凝土等刚性结构相比，两者最大区别在于设计建造结构时风荷载是否作为重要的影响因素来考虑.因此对于膜结构表面风压分布特点和影响因素的研究很有必要.

计算流体动力学数值模拟，即CFD(Computational fluid dynamics)数值模拟，是在风工程中应用越来越多的一种利用计算机来模拟计算结构各项特征的方法[4].CFD数值模拟还广泛的应用在其他许多领域中，张兆鑫等[5]利用CFD数值模拟方法研究了小型风机非扭曲叶片的气动性能，认为可通过设计变量风机转速和安装角提高其气动性能；马剑等[6]采用RNGk—ε湍流模型对建筑群周边的风环境进行数值模拟，认为CFD数值模拟方法能够较好的预测建筑群周围的风环境状况；谭堂州[7]对鞍形和伞形的膜结构进行分析，认为数值模拟方法能够较好的取代风洞试验.上述案例都很好地证明了CFD数值模拟的可行性.多跨鞍形膜结构作为工程中常用的一种结构形式，其周围的流场及表面的风压分布将更为复杂.采用基于FLUENT软件的CFD数值模拟方法对其表面的风压分布规律和影响因素进行研究，可为此种类型的结构抗风设计提供参考.

1计算模型

1.1建模方法

鞍形膜结构为曲面结构，首先需要利用有限元软件ANSYS对其进行找形，将得出的膜结构形状的几何外形提取出来，导入ICEM CFD中，创建外流场域，对外流域进行四面体网格划分，对膜结构近壁面的网格适当加密，再将网格导入FLUENT软件中并采用RNGk—ε湍流模型和SIMPLE分离算法完成对膜面风压特性的分析.

1.2模型参数

选取膜面初始预张力、风向角和矢跨比三个参数进行分析.膜面初始预张力T0分别为2，3，4 kN/m；风向角α分别为0°，45°，90°；矢跨比f/L分别为1/4，1/8，1/12.

多跨鞍形膜结构的原型为浙江工业大学朝晖校区新教学楼西侧的多跨鞍形膜结构，如图1所示，其结构计算模型如图2所示.该膜结构由8跨马鞍形膜面连成一体组成，长32 m，宽4 m，膜高点距离地面3.6 m，低点距离地面2.2 m(即f/L=1/8).膜面初始预张力T0=3 kN/m，张拉刚度Et=255 kN/m，泊松比γ=0.3，膜厚度t=1 mm.结构的角点均固定，所有边均为柔性索边界.边索的初始预张力为40 kN，索的弹性模量为150 GPa.在创建外流场域时，还需注意尽量小的影响计算模型周围空气的流动状态，故根据膜结构的尺寸大小，计算流域尺寸取为280 m×200 m×100 m，并且膜结构置于距离入口1/3处[8].流场网格划分如图3所示.

图1　膜结构原型Fig.1　The prototype of membrance structure

图2　结构原型计算模型Fig.2　The calculating model of structure

图3　非结构化网格示意图Fig.3　Schematic plot of unstructured grid

1.3计算参数的设置

入口边界的风速、湍动能、湍流耗散率和比耗散率等条件采用自定义程序UDF进行对接，取值与计算公式参见文献[9]中的算法设置.采用RNGk—ε湍流模型，使用SIMPLE分离算法，并用二阶迎风离散格式计算平均风压.风压系数的定义[10]为

(1)

2计算结果与分析

2.1膜面初始预张力影响分析

在以浙江工业大学内多跨鞍形膜结构为原型的基础上，改变膜面的初始预张力，分别取为2，3，4 kN/m，0°风向角工况下不同膜面初始预张力时多跨鞍形膜结构表面平均风压系数的模拟结果如图4所示.

从图4可以看出：在相同的0°风向角下，随着膜面初始预张力的增大，膜面受到正压的区域逐渐增加，负压区减小，正压区由原来约20%增加到约80%.设计时应当在极值正负压处格外注意.当膜面初始预张力由2 kN/m增加到4 kN/m时，除了在膜面高点处由于曲率过大而仍受负压外，在其后曲率减缓处，由于初始预张力的增大，膜表面结构分子间作用力加强，双向受拉的膜所受到的正压区域增多.

单跨鞍形膜结构在T0=4 kN/m，f/L=1/8，UDF中定义参考高度为10 m处的膜结构上下表面的风压系数图[4]如图5所示.对比发现，多跨和单跨鞍形膜结构表面风压的极值正压和极值负压均出现在膜面最高点及最低点的角点处，区别在于单跨鞍形膜结构的极值风压的正负值均出现在同一边的角点处，而多跨鞍形膜结构的极值风压正负值出现在对边的角点处.原因可能是单跨鞍形膜结构少了相邻跨的影响，随着曲率的变小又变大，风的碰撞分离作用由强变弱又变的稍微强一点，但都在同一侧，膜面风压的正负值不改变，仅改变大小.

2.2来流风向角影响分析

以浙江工业大学内多跨鞍形膜结构为模型，分别设置风向角为0°，45°，90°，模拟结果如图6所示.

图6　不同风向角多跨鞍形膜结构表面风压系数分布图Fig.6　Wind pressure coefficient distribution graph of multi-span saddle membrane in different wind angle

由图6可知：在大部分膜结构的最高点处，上表面受负压，下表面总是受正压；在大部分膜结构的最低点处，上表面受正压，下表面受负压.

当风向角为0°时，图6(a，b)中这种差异尤其明显.此时多跨鞍形膜结构的迎风面在膜结构的侧边，即只有结构的最高角点和最低角点那条边，在这条边上，膜表面的曲率的变化相对比较大，而曲率的变化与风向的流向既不平行也不垂直，成一定的角度，使得风的流动更加复杂.所以在这条短短的迎风边上的高低角点处均出现了极值风压.由图可见上表面中结构较高区域表现为负压，低点附近区域为正压，而下表面与上表面正好相反.在膜面的远离角点及边界的地方，即膜面的相对中心处，由于膜表面曲率变化减小，风的气流的碰撞分离效果减小，风压也逐渐减小趋于稳定和平缓.同时发现多跨鞍形膜面每一跨风压系数分布基本相同.

图6(c，d)中，当风向角为45°时，此时多跨鞍形膜结构的迎风面在膜结构边缘的角点，风流动以及碰撞分离均发生在角点附近.在第一跨最左边此迎风角点为最高点，故在其附近区域中上表面形成负压，下表面受正压，至于其附近的风压系数变化数值较大的原因，则是由于角点附近的膜面曲率较大，导致气流间的碰撞作用强烈.由于是多跨，受到相邻跨膜面的影响，在第一跨由于受到风的正面影响形成正压区后，在相邻的第二跨中心处形成了负压区.而此后每两跨膜面的风压系数分布相同.

图6(e，f)中，当风向角为90°时，靠近风一侧的膜面情况和风向角为0°时相同，随着气流的远离，气流作用减弱，膜上表面的极值负压和下表面的极值正压也迅速减小，但是减小的幅度先快后慢，最后趋于平缓接近0.图6(e)中，在每一跨的膜面高点处后方形成一片偏负压区，而低点处的后方形成一片偏正压区.

综上可以看出：风向角主要是通过改变膜面风压系数的极值分布状况进而改变控制整个膜面的风压系数分布情况.膜面风压系数极值一般存在于与风向角垂直接触处的曲率大的膜面处，其后方区域风压系数随着曲率的减小而减小，设计时要特别注意出现极值风压的位置.

2.3矢跨比影响分析

在0°风向角，膜面初始预张力T0=3 kN/m情况下，对矢跨比f/L=1/4，f/L=1/8，f/L=1/12工况下的多跨鞍形膜结构进行了模拟，获得的多跨鞍形膜结构膜面风压系数分布情况如图7所示.

由图7可知：矢跨比不改变鞍形膜结构表面的风压分布形式，即膜面风压的极值风压均出现在最高点和最低点的角点处，在最高点的上表面出现极值负压，最低点的上表面出现极值正压，下表面正好相反，随着曲率的减小，风压系数的绝对值逐渐减小.但不同矢跨比下膜结构表面的风压系数大小不同.

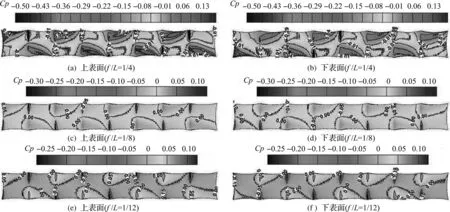
图7　多跨鞍形膜结构表面风压系数分布图Fig.7　Wind pressure coefficient distribution graph of multi-span saddle membrane

当矢跨比为1/4时，由于整体膜面较大的曲率，风的碰撞分离作用强烈，膜表面出现极值风压的范围较大，膜表面的风压系数变化梯度也较大.随着矢跨比的减小，膜表面曲率随之减小，多跨鞍形膜结构表面越来越平缓，膜面风压系数变化梯度遂逐渐减小，分布趋于均匀，膜表面受正压区域变小，迎风面边缘的高点所受负压即风的吸力也在变小.随着矢跨比的改变，多跨鞍形膜结构膜面迎风面前缘处受影响较大，其余地方受影响较小，因此要特别注意迎风面前缘的设计.

3结论

数值模拟计算可以较好的反映出膜面风压的分布特点，也可以很清楚的看到在各个参数条件下膜结构表面风压系数的变化规律.通过改变和调整相应参数，如在软件中模拟并改变所设计膜结构的膜面初始预张力和矢跨比等参数，使膜结构更加稳定安全.膜面初始预张力主要改变多跨鞍形膜结构表面所受风压的正负，膜面初始预张力越大，膜面所受正压区域越大.风向角对于膜面风压分布的影响主要是通过改变与之垂直接触处的迎风面前缘角点处的极值风压，随着曲率的减小，角点后方的风压系数绝对值逐渐减小.矢跨比对多跨鞍形膜结构表面迎风面前缘处影响较大，对其余部分影响较小.

参考文献：

[1]于向春．膜结构在大跨度建筑上的运用[J]．中外企业家，2014，41(1):68-72．

[2]陈新礼，沈世钊，向阳．鞍形薄膜结构的风振响应分析及风振系数[J]．天津城市建设学院学报，2001(9):212．

[3]于磊．基于向量式有限元的膜结构褶皱与碰撞接触分析[D]．杭州：浙江大学，2014．

[4]吴奎．基于CFD理论建筑膜结构风荷载数值模拟研究[D]．重庆：重庆大学，2013．

[5]张兆鑫，赵元虎，徐奔驰．基于CFD法的小型风机非扭曲叶片气动性能分析[J]．浙江工业大学学报，2013，41(1):68-72．

[6]马剑，程国标，毛亚郎．基于CFD技术的群体建筑风环境研究[J]．浙江工业大学学报，2007，35(3):351-354．

[7]谭堂州．膜结构风荷载的数值模拟研究[D]．广东：广东工业大学，2011．

[8]黄本才，汪丛军．结构抗风分析原理及应用[M]．2版．上海：同济大学出版社，2008．

[9]张建胜，周锋，卢成原，等．典型低矮双坡屋盖平均风压的数值模拟[J]．浙江工业大学学报，2014，42(3):302-306．

[10]中国建筑科学研究院．建筑结构荷载规范：GB 5009—2012[S]．北京：中国建筑工业出版社，2012．

(责任编辑：刘岩)

Numerical simulation study of the wind load on multi-span saddle membrane structures

ZHANG Jiansheng1, TAO Jin1, WANG Jiandong1, LI Weihang1, WU Liping2

(1. College of Civil Engineering and Architecture, Zhejiang University of Technology, Hangzhou 310014, China;2. Department of Urban Construction, Hangzhou Radio & TV University, Hangzhou 310012, China)

Abstract:The multi-span saddle membrane structure is a commonly used large-span spatial structure form in engineering. The wind load is a controllable fator in the structural design. The method of CFD numerical simulation is used to study the average wind pressure characteristics and to analyze the effects of the initial pretension on the membrane surface, the wind angle, and the rise-span ratio on the wind pressure distribution characteristics of multi-span saddle membrane structures. The results show that the initial pretension on the membrane surface mainly affects the size of the positive wind pressure area on the membrane surface. The larger the initial pretension on the membrane surface is, the larger the size of the positive wind pressure area is. The wind angle will change the positive or negative extremum of the wind pressure distribution and the positive or negative extremum generally appears at the edge perpendicular to the wind angle. The wind pressure coefficient of the membrane surface is influenced by the rise-span ratio but the wind pressure distribution is, on the whole, the same.

Keywords:multi-span saddle membrane structure; CFD numerical simulation; wind pressure distribution; effect

收稿日期：2015-11-11

基金项目：浙江省科技厅公益技术应用研究项目(2014C33031)；浙江省大学生科技创新活动计划暨新苗人才计划项目(2014R403077)

作者简介：张建胜(1981—)，男，浙江乐清人，副教授，博士，主要从事结构抗风研究，E-mail:jszhang@zjut.edu.cn.

中图分类号：TU312.1

文献标志码：A

文章编号：1006-4303(2016)04-0446-05