FSAE赛车车架结构的拓扑优化设计

李　芳，何婷婷

(浙江工业大学 机械工程学院，浙江 杭州 310014)

FSAE赛车车架结构的拓扑优化设计

李芳，何婷婷

(浙江工业大学 机械工程学院，浙江 杭州 310014)

摘要：为提高FSAE赛车车架的力学性能并实现轻量化，对赛车车架进行了拓扑优化设计.首先，对车队设计的初始车架进行强度和刚度分析.然后，根据车架的总体尺寸建立壳体CAD模型，将CAD模型保存成ParaSolid格式，并将几何模型导入HyperWorks中，用户配置模块设置为OptiStruct，对几何模型进行几何清理、划分单元、分配材料属性，建立用于拓扑优化的有限元模型，进行拓扑优化计算.根据拓扑结构，结合大赛规则和车架上各部件的装配要求设计出新车架.对新车架进行有限元静力学分析，包括几种典型工况下的强度和刚度分析，新车架的分析结果验证了结构设计的合理性，通过与初始车架分析结果相比较，表明了拓扑优化设计方法对赛车车架的设计具有可行性和有效性.

关键词：FSAE赛车；车架；拓扑优化；有限元分析；强度；刚度

连续体结构拓扑优化和离散结构的拓扑优化是拓扑优化的两个主要研究方向.连续体结构拓扑优化是把可设计空间划分成有限个壳单元或者体单元，并赋予材料属性进行拓扑优化设计.例如HAMMER V B等[1]对承受着方向和位置均变化的载荷的连续体结构的拓扑优化问题进行了理论研究，并且给出了算例验证.ZHOU M[2]等讨论了施加棋盘格约束和最小尺寸控制对拓扑优化结构的影响.CHANG J W等[3]对压缩机支架进行了典型工况下的拓扑优化设计.离散结构拓扑优化是在可设计空间内建立一个基结构，这个基结构是由有限个梁单元组成的，可设计空间内单元的删除与保留是根据相应的算法来确定的，保留下来的单元构成最终的拓扑结构，从而实现离散结构的拓扑优化设计.例如ROZVANY G等[4]讨论米歇尔桁架理论的一些缺点.王跃方等[5]对与离散结构的拓扑优化设计相关的问题进行了研究，对离散型优化模型的合理性进行了探讨，得出全局约束和截面设计变量的离散程度会影响最优拓扑结构.

对某FSAE赛车桁架式车架结构设计采用连续体拓扑优化方法，建立由有限个壳单元组成的封闭的壳体有限元模型，采用变密度法对赛车车架结构进行多种工况优化.参考优化计算出来的拓扑结构确定车架整体的桁架结构；结合大赛对车架结构的要求以及车身各部件的装配要求，设计出满足所有约束条件的车架结构；然后，再对车架进行了强度、刚度和自由模态分析，验证设计出的车架结构满足要求，确保可以安全地参赛.

1初始车架的有限元分析

车队根据《中国大学生方程式汽车大赛规则(2015最终版)》和车架上各部件的装配要求，在Solidworks建立初始车架的CAD模型，如图1所示.选用了2种不同管径与壁厚的钢管，尺寸分别为φ25.4 mm×2.4 mm和φ25.4 mm×1.6 mm.车架的材料是30CrMo钢管，弹性模量E=2.11×105MPa，泊松比μ=0.279，密度ρ=7 850 kg/m3，车架的总质量约为38 kg.

1.1强度分析

对赛车满载时在赛道上行驶时的弯曲工况、紧急制动时制动工况和在弯道行驶时的弯扭组合工况下的车架进行了等效静强度分析.由于车架采用的是双横臂独立悬架，为简化计算，约束悬架上、下摆臂与车架管件铰接处的中点，这样只需对8个点施加边界约束，约束点自由度约束见表1，其中纵向为x轴，竖直方向为y轴，横向为z轴.弯曲工况下车架的静态载荷乘上一个动态系数，取2.5，制动工况下的动态系数取1.5，制动减速度取为13.7 m/s2.弯扭组合工况下的动态系数取1.5，侧向加速度取为8.8 m/s2[6].车架的静态载荷如表2所示.车架在各个工况下的强度分析是在ANSYS软件中完成的[7-8].由于细长梁的控制因素通常是弯曲正应力，因此选用弯曲正应力与屈服极限作比较.车架钢管选用的材料30CrMo钢管属于合金钢，其塑性性能较低碳钢略差，抗压性能比抗拉性能好，因此选用弯曲正应力中的拉应力与屈服极限作比较，图2为各个工况下的弯曲正应力云图.

表2　车架静态载荷

图2　初始车架弯曲正应力云图Fig.2　Bending normal stress contour of the initial frame

由图2和ANSYS的分析结果可得：弯曲工况下最大变形为3.1 mm，最大弯曲正应力为51.4 MPa，为拉应力，在驾驶舱底部.制动工况最大变形为1.9 mm，最大弯曲正应为30.6 MPa，为拉应力，在驾驶舱底部.弯扭组合工况最大变形约为11.2 mm，最大弯曲应力值为28.3 MPa，为拉应力，在车架内则侧边防撞杆与主环焊接点处.

1.2扭转刚度分析

参考国外参赛车队分析经验，大多数赛车队将车架扭转刚度作为设计重点，因此对扭转工况下的车架进行了数值模拟，计算出车架的扭转刚度值.约束车架与后悬架连接点3个方向x，y，z的位移，在车架与前悬架连接点处施加大小为1 000 N相反的y向力的作用，建立有限元分析模型，将分析所得施力点位置的位移值代入公式

(1)

其中：M=Fl；θ=πarctan[(δ1-δ2)/l]/180；l为悬架硬点间的距离；δ1，δ2分别为施力点在竖直方向的位移，分别为1.33 mm和-1.33 mm，将该数据代入计算，可得车架的扭转刚度约为101 929 N·m/rad.

1.3自由模态分析

利用ANSYS软件对车架进行自由模态分析分析[9]，选用Beam189单元对车架模型划分网格，网格均匀化划分，单元尺寸统一为50 mm，并赋予材料参数.选用Block Lanczos法提取车架在自由状态下的前4阶非刚体模态，如表4所示.振型方式先是车架整体振动，随着频率的提升变为大质量载荷安装位置处的局部振动，再是变为细长杆件的局部振动.由赛道上路面不平度引起的激振频率范围是1～20 Hz，由车轮动态不平衡引起的激振频率一般低于11 Hz[10].电机振动引起的激振频率大于200 Hz，且高阶模态车架的振动能量值远小于低阶模态下的振动能量值，可以忽略不计，又由于赛车行驶里程和持续时间短，所以短时间内高阶局部振动不足以引起车架的疲劳破坏，该车架满足动态性能要求.

表3　初始车架的固有频率及其振型

2车架的拓扑优化设计

2.1拓扑优化模型的建立

车架前环、主环和主环斜撑是根据《中国大学生方程式汽车大赛规则(2015最终版)》设计的，主环之间的横向管件是用来支承座椅靠背和头枕，属于不可设计区域.悬架安装位置点一旦确定，就不能再改变.结合浙江工业大学FSAE赛车队的设计参数，在HyperWorks的OptiStruct模块中，选择SHELL单元，定义单元厚度，单元尺寸为20 mm，划分网格.建立赛车的拓扑优化有限元几何模型，该模型包含12 169个节点，12 222个单元.如图5所示，主环及主环斜撑、前环、位移约束点处杆件和靠椅支撑杆件均为不可设计区域，其余区域为可设计区域.

图3　车架的拓扑优化有限元模型Fig.3　Finite element model of frame topology optimization

2.2典型工况的约束与加载方式

分别对两种扭转、弯曲和弯扭组合四种工况进行了单工况的拓扑优化.扭转工况1约束方式为：约束左右悬架和右后悬架4个位移约束点的3个轴坐标方向的位移自由度，在左前悬架和右前悬架上方2个位移约束点分别施加大小为1 000 N相反的y向力的作用.扭转工况2约束方式为：约束左前悬架和右前悬架4个位移约束点的3个轴坐标方向的位移自由度，在左后悬架和右后悬架上方2个位移约束点分别施加大小为1 000 N相反的y向力的作用.根据表1,2提供的约束方式和负载信息，添加对应于弯曲和弯扭组合工况下的位移约束方式和载荷，得到有限元分析模型.

2.3定义约束条件与目标函数

车架许用应力公式[11]分别为

σp=σjp/K

(2)

σjp=σs/ns

(3)

式中：σp为许用应力；σjp为基本许用应力；K为折减系数，取值范围为1.1～1.2，取1.2；σs为屈服强度，车架统一采用30CrMo钢管，屈服强度为785 MPa；ns为基本安全系数，取值范围为1.2～1.5，取1.5.

由式(2，3)可算出许用应力约为436 MPa，作为所有设计变量的应力约束条件，以至多保留可设计区域10%材料约束作为体积约束条件.由于车架是左右对称的，添加对设计空间施加关于纵向对称面的对称约束的制造工艺约束条件.以可设计区域的应变能最小为目标函数，将优化参数DISCRETE设定为2.5，以提高优化结果的离散度.最后在材料插值模型方法为变密度法的OptiStruct优化模块中系统自行对可设计区域进行拓扑优化分析计算，从而寻求满足应力、体积和制造工艺约束条件的前提下，可设计区域实现最优的材料分布，获得概念性的拓扑结构，为车架整体桁架结构设计提供理论参考.

2.4拓扑优化结果及分析

拓扑优化后的最佳材料分布等值面图形如图6所示，显示密度值在0.3及以上.在扭转工况1的条件下，经过40次迭代运算达到收敛，由最佳材料分布等值面图形可以看出，优化出清晰的车架前部抗扭横向桁架结构，这为车架前部的桁架结构设计提供了参考.在扭转工况2的条件下，经过47次迭代运算达到收敛，优化出明显的车架尾部的抗扭桁架结构，这为车架尾部的桁架结构的设计提供了参考.在弯曲工况条件下，经过39次迭代运算达到收敛，在车架中部优化出明显的抗弯纵向和横向管件结构.在弯扭组合工况条件下，经过53次迭代运算达到收敛，在车架中部优化出明显的侧边防滚架区域的桁架结构.参考优化计算出来的拓扑结构可以初步确定车架整体的桁架结构.根据优化结果的材料堆积程度，设计出对应管件位置处的尺寸，材料堆积位置的截面直径和厚度选取比材料稀疏的位置截面直径和厚度相对较大的尺寸.

2.5车架结构CAD模型的建立

拓扑优化设计是一种概念性设计，拓扑结构极不规则，不符合加工和制造的要求，因此还需对车架结构进行详细地设计.车队设计组根据大赛规则中的设计要求，参考根据拓扑优化结果得到的理论，结合车架上各部件的装配要求，设计出了新的车架结构，并在Solidworks建立CAD模型，如图7所示，选用了6种不同管径与壁厚的钢管，分别为φ25.4 mm×2.4 mm，φ25.4 mm×1.6 mm，φ25.4 mm×1.25 mm，φ20 mm×1 mm，φ14 mm×1 mm，φ10 mm×1 mm最终得到的车架质量为33 kg.

图4　最佳材料分布等值面图形Fig.4　Optimal material distribution contour

图5　新车架CAD模型Fig.5　CAD 3D model of the new frame

3新车架的有限元分析

3.1强度分析

车架结构设计出来后，需要对车架进行强度

和刚度分析，判断车架是否符合静力学要求.对新车架施加与初始车架同样的边界约束条件和载荷，在ANSYS中对赛车车架在各个工况下约束与承载进行数值模拟，图6为各个工况下的弯曲正应力云图.

由图6得和ANSYS的分析结果可得：弯曲工况最大变形约为1.1 mm，最大弯曲正应力为16.9 MPa，为拉应力，在车架底部与主环管件焊接点处.制动工况最大变形约为0.9 mm，最大弯曲正应力为9.0 MPa，为拉应力，在车架底部与主环管件焊接点处.弯扭组合工况最大变形约为2.9 mm，最大弯曲正应力为20.1 MPa，为拉应力，在车架内则侧边防撞杆与主环焊接点处.

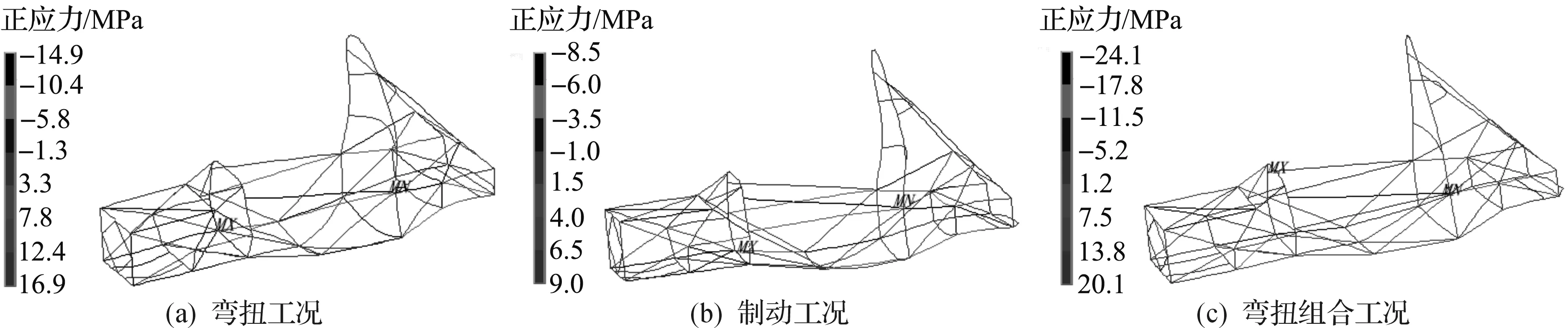
图6　新车架弯曲正应力云图Fig.6　Bending normal stress contour of the new frame

3.2刚度分析

建立有限元分析模型，将分析所得施力点位置的位移值1.24 mm和-1.24 mm代入式(1)，计算得车架的扭转刚度为105 596 N·m/rad.美国康奈尔大学1999年FSAE桁架式车架的扭转刚度为124 217 N·m/rad，国外方程式赛车的扭转刚度在57 295～229 183 kN·m/rad[12]，该车架的扭转刚度落在这个范围内，表明该车架结构设计的合理性.

3.3自由模态分析

选用Block Lanczos法提取新车架在自由状态下的前4阶非刚体模态，如表4所示.振型方式与初始车架的振型方式保持一致，但是新车架的第1阶固有频率比初始车架的有所提高，这是由于车架整体刚度提高导致的.同样，新车架也满足动态性能要求，可以避免共振破坏.

表4　新车架的固有频率及其振型

3.3初始车架与新车架的对比与分析

表5为初始车架与新车架各项性能的对比，由表5得出：弯曲工况、制动工况和弯扭组合工况下车架的最大应力值和最大变形值均较大幅度的减小了，表明新车架的强度性能相较于初始车架大幅度地增加.而新车架的抗扭转刚度和第1阶固有频率相较于初始车架分别增加了7.3%和10.5%，表明新车架抗扭转性能和刚度得倒提升.新车架的质量相较于初始车架的质量下降了13.2%，实现了轻量化的目标.

表5　初始车架与新车架的对比

4结论

通过对车架结构的拓扑优化设计，实现了满足应力、体积和制造工艺等约束条件的前提下，获得车架可设计区域最优的材料分布，即概念性的拓扑结构，并以此为参考设计出车架整体桁架结构.分析结果表明根据拓扑优化结果设计出的新车架相较于初始车架在强度和抗扭转刚度的力学性能和振动性能得到大幅度地提升，新车架的质量相较于初时车架有所减少，表明了拓扑优化的可行性和有效性.此外，由仿真结果可以看出：优化后的车架最大弯曲正应力远小许用应力，存在应力富余，因而后续可以对车架局部管件进行尺寸优化并对其力学性能加以验证，得到满足力学性能的质量更轻的车架.

参考文献：

[1]HAMMER V B， OLHOFF N. Topology optimization of continuum structures subjected to pressure loading[J]. Structural and multidisciplinary optimization，2000，19(2)：85-92.

[2]ZHOU M， SHYY Y K， THOMAS H L. Checkerboard and minimum member size control in topology optimization[J].

Structural and multidisciplinary optimization，2001，21(2)：152-158.

[3]CHANG J W， LEE Y S.Topology optimization of compressor bracket[J]. Journal of mechanical science and technology，2008，22(9)：1668-1676.

[4]ROZVANY G. Some shortcomings in Michell’s truss theory [J]. Structural optimization，1997，13(2)：203-204.

[5]王跃方，孙焕纯，黄丽华.离散变量结构拓扑优化设计研究[J].固体力学学报，1998，19(1)：59-63.

[6]赵帅，隰大帅，王世朝.FSAE赛车车架的强度和刚度分析[J].计算机辅助工程，2011，20(4)：53-56.

[7]崔钦淑，郭颜凯.RC Z形柱框架节点拟静力试验有限元分析[J].浙江工业大学学报，2015，43(6)：690-694.

[8]苏友文，马倩雯，李超飞，等.二次受力下预应力碳纤维布加固混凝土梁抗弯性能研究及数值模拟分析[J].浙江工业大学学报，2014，42(4)：378-387.

[9]杨庆华，夏航，王志恒，等.颤振冷挤压振动台设计与振动特性研究[J]，浙江工业大学学报，2015，43(1)：24-29.

[10]纪飞，李静，马泽宏.FSAE赛车车架的自由模态分析[J].拖拉机与农用运输车，2014，41(6)：26-29.

[11]成大先.机械设计手册[M].北京：机械工业出版社，2009.

[12]王家豪.FSAE管阵式车体骨架结构设计与析[R].广州：华南理工大学，2010.

(责任编辑：刘岩)

Topology optimization of FSAE car frame

LI Fang, HE Tingting

(College of Mechanical Engineering, Zhejiang University of Technology, Hangzhou 310014, China)

Abstract:In order to improve the mechanical property and reduce the weight of FSAE car frame, topology optimization design for the car frame was conducted. At first, strength and stiffness analysis of the initial frame which was designed by the car team was conducted. Then, set up the CAD model of frame, saved the CAD model into ParaSolid format, used OptiStruct module of HyperWorks to clean up the geometric model, divide mesh and assign material properties for building topology optimization model of the car frame. Referring to the topological structure, combined with the competition rules and requirements of assembling for each part of the frame, a new FSAE car frame structure was proposed. The finite element analysis of the frame structure was conducted which includes strength and stiffness analysis in typical working conditions. The results verify that the structure design of frame is rational. By comparing the analysis results of the initial frame and the results of the new frame，it shows that the topology optimization design of the car frame is feasible and effective.

Keywords:FSAE car; frame; topology optimization; finite element analysis; strength; stiffness

收稿日期：2015-11-23

作者简介：李芳(1957—)，女，浙江杭州人，副教授，硕士生导师，研究方向为结构有限元分析，E-mail:lif1110@163.com.

中图分类号：TH12

文献标志码：A

文章编号：1006-4303(2016)04-0369-06