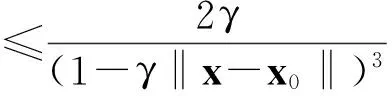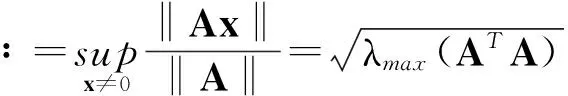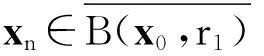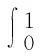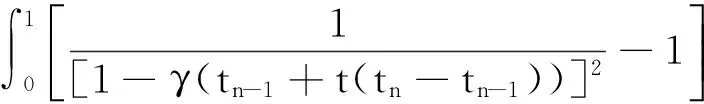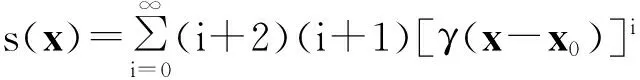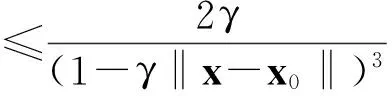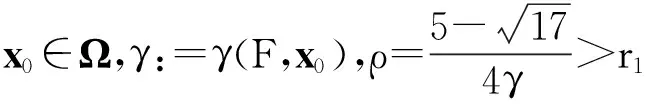解变分不等式的简单牛顿法的收敛性

周　彪，李素兰

(浙江工业大学 理学院，浙江 杭州 310023)

解变分不等式的简单牛顿法的收敛性

周彪，李素兰

(浙江工业大学 理学院，浙江 杭州 310023)

摘要：牛顿法作为求解变分不等式问题的一个重要方法，它的收敛性一直是各位学者研究的一个核心问题.当变分不等式中的函数F在内满足γ-条件时，证明了由牛顿法产生的迭代点列是适定的，而且解的序列可以被构造出来的{tn}序列控制收敛到一个变分不等式的最优解.考虑到F在内满足γ-条件这个区域性条件给进一步的研究带来了困难，因此引入了解析函数，给出了F是解析函数条件下的牛顿法的收敛性结果.数值实验表明算法是有效的.

关键词：牛顿法；变分不等式；γ-条件；半局部收敛；解析函数

变分不等式(Variational inequality)首先由Hartman和Stampacchia[1]在1966年提出，最初是用来研究偏微分方程的，它在数学、工程、物理和经济等领域有着广泛的应用背景.作为非线性互补问题的推广，它的提出统一了优化问题和均衡问题的研究，并且在数学领域中作为大量数学问题实际求解的统一框架.实际生活中的许多问题都可以归结为(或松弛成)一个凸优化问题，而凸优化的一阶必要性条件就是一个单调变分不等式.因此用变分不等式研究凸优化的求解问题，就像微积分中用导数求一元函数的极值，常常会带来很大的方便，这使得它成为数学规划中一个十分热门的研究课题[2-6].

1理论基础与符号说明

1.1符号说明

1)Rn表示n维欧式向量空间，令Ω→Rn，F:Ω→Rn表示映射F的值域和定义域都是Rn的非空子集.

2)‖x‖：向量x的2-范数.

3)‖A‖：矩阵A的2-范数.

B(x0,ρ)∶={y∈Rn|y-x0

1.2理论基础

下面给出变分不等式的一般形式：

给定一个Rn中的非空子集Ω和一个函数F:Ω→Rn,变分不等式问题记为VIP(Ω,F),是指求x*∈Ω，使得

(y-x*)TF(x*)≥0∀y∈Ω

(1)

文献[13]中提到了很多数值解法，其中牛顿法是最重要的方法之一.牛顿法解函数F(x)=0时的一般迭代格式为

F′(xn-1)T(xn-xn-1)=-F(xn-1)

n=1,2,3,…,∞

(2)

而在求解变分不等式时，序列{xn}是由以下不等式的解产生的：假设已知迭代起点x0∈Ω，则x1的解为

(y-x1)T(F(x1)+F′(x0)(x1-x0))≥0

∀y∈Ω

那么假设xn-1存在，则xn为

(y-xn)T(F(xn-1)+F′(xn-1)(xn-xn-1))≥0

∀y∈Ω

(3)

的解.

定义1设Ω是Rn的一个非空的凸闭集，令ρ>0，γ>0，ργ<1.函数F:Ω→Rn在Ω上二阶可微且存在一个x0∈Ω，F′(x0)-1存在，若不等式

(4)

定义2数学上如果一个函数在邻域内的每个点都能够展开成幂级数，且收敛半径大于零，则我们称函数在邻域内是解析的.

2由牛顿法产生的序列{xn}的收敛性

2.1γ-条件

给定一个Rn中的非空子集Ω和一个函数F:Ω→Rn,变分不等式问题记为VIP(Ω,F)是指求x*∈Ω，使得

(y-x*)TF(x*)≥0∀y∈Ω

(5)

牛顿法作为求解变分不等式(5)最重要的方法之一，在求解xn时文献[13]考虑的是F在xn-1处的一阶导数信息，将算法简化为每次迭代都只考虑F在x0处的一阶导数信息.故其迭代格式如下:

假设已知迭代起点x0∈Ω，则x1的解为

(y-x1)T(F(x1)+F′(x0)(x1-x0))≥0

∀y∈Ω

(6)

那么假设xn-1存在，则xn为

(y-xn)T(F(xn-1)+F′(x0)(xn-xn-1))≥0

∀y∈Ω

(7)

的解.即xn为VIP(Ω,Fn-1)的一个解.记Fn-1(xn)∶=F(xn-1)+F′(x0)(xn-xn-1).

王兴华和韩丹夫教授[15]通过引入函数

(8)

改进了Smale点估计的结论.其中β>0,R满足

此时若将式(8)中的函数L定义为

则函数h(t)为

(9)

并且定义了一个序列{tn}为

t0=0,n=0,1,…

(10)

其中h(t)满足式(9).

引理1假设A∈Rn×Rn是一个正定矩阵，x∈Rn，则有

证明回顾矩阵2-范数的定义

‖xn+1-xn‖

(11)

且{xn}收敛到变分不等式的一个解x*.

证明首先证明由牛顿法产生的序列{xn}是适定的：因为F′(x0)是正定的，那么显然Fn-1(x)是严格递增的.而Ω是Rn的一个非空的凸闭集，所以VIP(Ω,Fn-1)有一个唯一解xn.即如果F′(x0)是正定的，则由式(7)牛顿法产生的序列是有意义的[12].

(xn+1-xn)TFn-1(xn)=(xn+1-xn)T·

(F(xn-1)+F′(x0)(xn-xn-1))≥0

(12)

(xn-xn+1)TFn(xn+1)=(xn-xn+1)T·

(F(xn)+F′(x0)(xn+1-xn))≥0

(13)

合并式(12，13)，并移项得

(xn-xn+1)TF′(x0)(xn-xn+1)≤

(xn-xn+1)T[F(xn)-F(xn-1)-

F′(x0)(xn-xn-1)]

(14)

(xn-xn+1)TF′(x0)(xn-xn+1)≥

(15)

结合式(14，15)，有

(xn-xn+1)≤

(xn-xn+1)T[F(xn)-

F(xn-1)-F′(x0)·

(xn-xn-1)]

移项化简得

‖xn+1-xn‖≤‖F′(x0)-1‖‖F(xn)-F(xn-1)-

F′(x0)(xn-xn-1)‖=

t(xn-xn-1))-F′(x0)‖·

‖xn-xn-1‖dt

(16)

‖xn-xn + 1‖‖xn - 1+ t(xn-xn - 1)-x0‖dλdt =

tn+1-tn

(y-x*)T(F(x*)+F′(x0)(xn-xn-1))=

(y-x*)T(F(x*))≥0成立，即{xn}收敛到变分不等式的一个解x*.得证.

2.2 在解析函数上的应用

(17)

如果F′(x0)不可逆，则定义γ(F,x0)=∞.因此，若

F′(x0)可逆，则由解析性得γ(F,x0)有界.以下引理说明当函数F是解析的，则F一定满足γ-条件.

证明因为函数F是解析的,可以写成幂级数的形式为

所以

又因为F′(x0)可逆，结合(17)式得

(18)

(19)再次对(19)等式两边同时乘以γ(x-x0)，并相减，得

移项得

再结合(18)式得

接下来，我们得到了一个关于函数F是解析函数的牛顿法序列收敛性的推论.

‖xn+1-xn‖

(20)

且{xn}收敛到变分不等式的一个解x*.

3数值结果

任意x=(ξ1,ξ2)∈R2

表1牛顿迭代的次数与数值结果

Table1ThenumberofiterationsandNumericalresultsofNewton

迭代数/次序列{xn}0(0.95,0.96)1(0.9463,0.9421)2(0.9397,0.9377)3(0.9333,0.9308)4(0.9298,0.9285)5(0.9255,0.9266)6(0.9229,0.9232)7(0.9214,0.9221)8(0.9210,0.9219)9(0.9209,0.9213)10(0.9206,0.9206)11(0.9202,0.9205)12(0.9201,0.9203)13(0.9201,0.9202)14(0.9201,0.9202)

算法在第14步趋于最优解x*=(0.92,0.92).说明牛顿算法是有效的.

4结论

参考文献：

[1]HARTMAN P, STAMPACCHIA G. On some nonlinear slliptic differential functional equations[J]. Acta mathematica,1966,115:153-188.

[2]FAROUQ N E. Pseudomonotone variational inequatlities: convergence of proximal methods[J]. Journal of optimization theory and applications,2001,109(2):311-326.

[3]SALMON G, NGUYEN V H,STRODIOT J J. Coupling the auxiliary problem principle and epiconvergence theory to solve general variational inequalities[J]. Journal of optimization theory and applications,2000,104(3):629-657.

[4]PENG J M, FUKUSHIMA M. A hybrid Newton method for solving the variational inequalities problems via the d-gap functiona[J]. Mathmatical programming,1999,86:367-386.

[5]WU J H. Long-step primal path-following algorithm for monotone variational inequalities problems[J]. Journal of optimization theory and applications,1998,99(2):509-531.

[6]FAROUQ N E. Pseudomonotone variational inequalities: convergence of the auxiliary problem method[J]. Journal of optimization theory and applications,2001,111(2):305-326.

[7]KANTOROVICH L V,AKILOV G P. Functional analtsis[M].Qxford:Pergamon,1982.

[8]KANTOROVICH L V. Functional analysis and applied mathematics[J]. Uspekhi matematicheskikh nauk, 1948(3)：89-185.

[9]SMALE S. Newton’s method estimates from data at one point[M]. New York: Spring,1986：185-196.

[10]SMALE S. Compexity theory and numerical analysis[J] Acta number，1997(6):523-551.

[11]WANG X H, HAN D F. Criterion α and Newton’s method[J]. Applied mathematics-a journal of chinese universities，1997,19:96-105.

[12]CHANG D C, WANG J H, YAO J C. Newton’s method for variational inequality problems: Smale’s point estimate theory under the -condition[J]. Applicable analysis,2013(1):44-55.

[13]FACCHINEI F, PANG J S. Finite-dimensioanl variation inequalities and complementarity problems[M]. New York: Springer-Verlag，2003.

[14]王兴华，韩丹夫.弱条件下的α判据和Newton法[J].计算数学，1997(2):103-112.

[15]WANG X H. Convergence of Newton’s method and inverse function theorem in banach space[J]. Mathematics of computation,1999，68(1):169-186.

[16]WANG X H. Convergence of Newton's method and uniqueness of the solution of equations in Banach space[J]. IMA journal of numberical analysis，2000(20):123-134.

[17]鲍吉锋.平衡问题和优化问题若干算法的收敛性分析[D].杭州：浙江大学，2013.

(责任编辑：陈石平)

Convergence of Newton method for solving variational inequalities

ZHOU Biao, LI Sulan

(College of Science, Zhejiang University of Technology, Hangzhou 310023, China)

Abstract:Newton method is an important method for solving the problem of variational inequalities, the convergence of the algorithm has been a core issue for the scholars. When the function F in variational inequalities satisfies γ-conditions in , it is proved that the iterative dot sequence produced by the Newton method is valid and can be controlled to converge to an optimal solution of the variational inequalities by a sequence {tn}, which is constructed out. Taking into account that the regional conditions of the function F satisfies γ-conditions in makes more difficult for further study, analytic functions is introduced. The convergence of Newton method under the condition that the F is analytic function is given. Numerical experiments show that the algorithm is effective.

Keywords:Newton method; variational inequalities; γ-conditions; semilocal convergence; analytic functions

收稿日期：2015-12-17

基金项目：国家自然科学基金资助项目(11371325 )

作者简介：周彪(1991—)，男，浙江台州人，硕士研究生，研究方向为最优化算法与理论，E-mail：zhoubiaozjut@163.com.通信作者：李素兰副教授，E-mail：sulanli@zjut.edu.cn.

中图分类号：O224

文献标志码：A

文章编号：1006-4303(2016)04-0461-05