法向约束下B样条曲线拟合的实编码GA算法

寿华好，胡良臣

(浙江工业大学 理学院，浙江 杭州 310023)

法向约束下B样条曲线拟合的实编码GA算法

寿华好，胡良臣

(浙江工业大学 理学院，浙江 杭州 310023)

摘要：提出一种带有法向约束的遗传算法求解曲线逼近问题的方法，即将带有法向约束的问题通过惩罚函数的方法转化为无约束的最优化问题，然后以遗传算法(GA)取代传统的反求线性方程组系统或几何构造等方法求解最佳控制点，从而实现较为高效率逼近的同时很大程度上简化了计算流程，更加易于理解.并且通过实验对比了该方法在不同节点向量以及在不同的内节点数量情况下的曲线逼近程度的实际效果，数据实验表明该方法解决带法向约束的逼近问题切实可行.

关键词：离散数据;B样条逼近;遗传算法;法向约束

数据拟合的相关技术越来越多地应用到逆向工程[1](Reverse engineering)的各个领域.通过激光扫描、结构光源转换仪或者X射线断层成像等技术在实际物体上获取测量数据，在无法对该物体进行生产的前提下，利用这些扫描下来的离散数据点进行数据拟合，可以对原模型或产品进行一个大致的模型重建及功能恢复，这在几何分析以及图像分析领域应用广泛.但有些情况下，获取的数据点可能不止简单的坐标信息，对于每一个或者个别的数据点可能包含一些约束形状的条件，例如在光学工程领域，带有法向约束的数据点的处理.这里笔者主要考虑的是法向约束下的曲线拟合.首先，曲线方程的选取对曲线的逼近程度有着非常重要的作用，由于B样条曲线的各种优良的属性[2]，许多研究学者都使用B样条曲线作为逼近函数去处理得到的离散数据点.B样条理论是由Schoenberg在1946年提出来的，1972年De Boor和Cox分别独立给出了B样条的标准算法[2].Gordon和Riesenfeld把B样条应用于形状的描述，从而提出了B样条方法.B样条基取代Bernstein基，很好地解决了局部控制的问题，又轻而易举地解决了连续性拼接问题，从而使得自由曲线曲面的重构成为可能.

对于型值点带有法向、切矢亦或者是曲率等条件约束的曲线插值或逼近问题，许许多多的学者做出了不懈的努力.诸如Piegl等[2]提出的点-切向约束的B样条曲线插值算法，Gofuku等[3]提出的点-切向/点-法向的B样条曲线插值几何算法，Abbas等[4]提出的满足数据点及法向、曲率约束的三次B样条插值的构造算法，Shoichi等[5]提出的切向曲率约束的三次均匀B样条插值的几何算法，星蓉生等[6]提出的三次均匀B样条曲线插值数据点及其切矢的PIA算法以及胡巧莉等[7]提出的基于几何构造的法向无偏移的带法向约束的三次均匀B样条曲线插值算法.以上学者提出的各种算法均是基于反求线性方程系统或者是通过几何构造的方法来解决此类问题的.但是利用解方程组是在节点和参数化固定的前提下进行的，所以难以发挥B样条方法的极大自由性；几何构造方法一般要求节点均匀，也存在一定局限性.鉴于反求方程组和几何构造方法的局限性，利用各种人工智能算法[8-13]求解以及优化曲线拟合问题是当今曲线拟合问题领域的一大热门.笔者将人工智能的遗传算法用到解决带有法向约束的曲线逼近的问题上，将带有法向约束的数据点的曲线逼近问题转化为基于遗传算法的无约束的最优化问题来解决，避免了传统方法的反求线性方程系统以及几何构造的复杂计算和一些局限性，仅仅通过适应度函数来评价曲线拟合的好坏，无需人为干涉和多余的规则考虑，易于理解，简单方便，实验结果证明该方案是有效的.

1问题描述及模型建立

考虑给定M+1个二维或三维数据点di,i=0,1,…,M且对于每个数据点带有一个法向约束条件li,i=0,1,…,M，现需找到一条曲线S去逼近给定的数据di,i=0,1,…,M且对于数据点在曲线上的对应参数处满足法向约束条件.由于B样条曲线所具有的几何不变性、凸包性、局部支撑性、变差减缩性等诸多的优良性质，所以取B样条曲线作为逼近曲线，此时问题变为寻求一条形状合适且误差精度相对令人满意的样条参数曲线S(t)=S.假定与数据点di,i=0,1,…,M对应的参数值是ti，则带法向约束的B样条曲线逼近问题可以用两个方程组成的方程组表示为

(1)

式中：εi为数据点di的拟合误差；S′(ti)为逼近曲线在参数值ti处的一阶导矢.一条p次B样条曲线可以表示为

(2)

它的一阶导矢为

(3)

式中：二维或三维点集为{Pj}为样条逼近曲线的n+1个控制顶点；Nj,p(u)为p次B样条基函数，其定义由deBoor和Cox[2]递推给出：

(4)

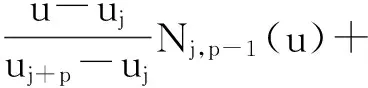
(5)

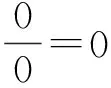
由式(2～5)，且设控制顶点集{Pi}为未知变量，则式(1)中的带法向约束的B样条曲线逼近问题可以化为带有等式约束的最小值优化问题，即

(6)

式中‖·‖为平方范数.

对于以上问题的描述，设计的算法框架如图1所示，具体实现过程在下文中将会详细叙述.

图1　基于GA的法向约束下样条曲线拟合算法流程图Fig.1　Flowchart of the GA-based B-spline curve approximation algorithm with normal constraint

2法向约束下B样条曲线逼近的实现

由于使用传统的计算方法对带约束的曲线逼近问题求解复杂性，且基于遗传算法对求解带约束问题的困难性基础上，这里将使用一种在优化模型上加惩罚函数的方法将带约束的问题，转化为无约束的问题，进而使用遗传算法加以解决.

2.1无约束问题的转化

为了实现式(1)中的等式约束S′(ti)·li=0，将允许严格的等式约束出现适当的误差，即：S′(ti)·li≈0.这样在误差允许的范围内，可保证给定数据点的法向跟逼近曲线的一个大致的贴合.接下来将上式的平方和作为一个惩罚函数，整理式(1，6)，可得最终需要的待求解变量为{Pj}的一个数学模型为

Q(P0,P1,…,Pn,C0)=F(P0,P1,…,Pn)+

C0G(P0,P1,…,Pn)=

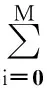
j=0,1,…,n

(7)

式中C0作为惩罚系数，在这里设为1.最终将利用遗传算法对(7)式寻求最优解.

2.2节点向量的设置

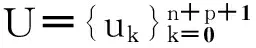
2.2.1均匀节点向量

均匀节点向量是最简单的节点配置方法.它的选取不受数据点的参数化的影响，内节点的计算方法为

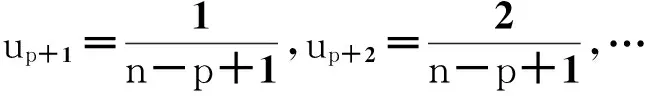
(8)

2.2.2平均节点向量

平均节点向量是由德布尔[2]提出来的，并且它的计算依据跟数据点的参数化有关系，内节点计算方式为

(9)

2.2.3皮格尔逼近节点向量

这种方法是由皮格尔和蒂勒[2]针对曲线逼近的情况提出来的，计算方法为

uj+p=(1-(ja-i))ti-1+(ja-i)ti

(10)

采用了皮格尔逼近节点向量，在实验中将给出选取不同的节点向量时的曲线逼近情况的对比.

2.3数据点参数化设置

对于数据点参数化，这里采用积累弦长参数化[3].参数ti通过点之间的位置关系进行估计，估计公式为

(11)

式中参数ti为数据点di在其B样条逼近曲线上对应的参数值.

3遗传算法介绍及相关算子和参数设置

遗传算法(Geneticalgorithm)是一种模拟生物界物种繁衍进化过程中的遗传规律(物竞天择，适者生存的机制)演化而来的随机性的全局优化方法.起初J.Holland教授于1975年提出了遗传算法的基本理论与基本方法，其最为显著的优势是依照大自然进化规律直接对可行解本身进行操作，除去了函数的求导和连续性等数学条件的限制；有着很好的内在并行结构以及全局优化的能力；自适应优化搜索空间并调整搜索的范围，在寻优过程中没有人为的任何干预，同样也不需要确定任何规则，其唯一的评价标准就是适应度函数.有鉴于遗传算法的优良性质，人们广泛地将其应用于组合优化、自适应控制、机器学习及信号处理等领域.现已成为人工智能领域的关键技术之一.

3.1相关算子以及参数设置

标准的遗传算法采用二进制编码，但是随着二进制编码应用于各个领域，越来越多的研究者发现，在处理高维的优化问题或者在要求问题解的精度足够大的时候，二进制编码需要足够长的码串，严重影响了其搜索最优解的效率.但是采用实数编码形式的话，则有效地避免了这一问题.鉴于实数编码直接将实数作为染色体进行遗传算法的操作，所以它在继承了二进制编码所有优点的同时，还降低了算法的复杂度，提高了效率，能够更快更加合理地调节种群的局部解.

同二进制编码一样，实数编码的遗传算法同样包括了3个基本操作，选择、交叉及变异：

1) 选择算子：选择算子采用随机竞争选择(Stochastictournament)外加精英保留选择(Elitistmodel)双机制.首先对种群进行精英保留，对种群中最好的个体直接复制到下一代，然后剩余个体随机竞争，每次按照轮盘赌选择机制(适应度高则被选中的几率就越大)选取一对个体，然后让选中的这两个个体进行比较，适应度高的个体则存活下来，如此直到选满种群大小为止.

2) 交叉算子：利用算术交叉的方法对种群个体操作.对于两个父代个体={,,…,}，={，，…，}，则子代产生方式如下：={，，…，},i=1,2，其中，=λ+(1-λ)，=λ+(1-λ)，λ为取常数时为均匀算数杂交，取变量时为非均匀算数杂交.另外交叉概率Pc取0.9.

4) 适应度函数：对式(7)求最小值的优化问题去负值，变为适宜遗传算法的求最大值的问题，取适应度函数如下：

fitness(X)=Fit(Q(P0,P1,…,Pn,C0))=

-Q(P0,P1,…,Pn,C0)

(12)

5) 变量：对于一组待求解的控制点P0(x0,y0),P1(x1,y1),…,Pn(xn,yn)，考虑到拟合曲线端点插值，设置变量X=X(X0,X1,…,X2n-3)，其长度为2(n-1)，对应于控制点的坐标为

X(x1,…,xn-1,y1,y2,…,yn-1)=X(X0,X1,…,X2n-3)

3.2算法描述

总结以上关于遗传算法以及相关参数的概述，给出以下关于带有法向约束的曲线拟合算法的描述：

Step 1输入待拟合数据di及其对应法向li,i=0,1,…,M.

Step 2数据点参数化，合适的节点向量(选用皮格尔节点向量)选取以及有效的适应度函数(见式(12))的建立.

Step 3遗传算法相关参数的设置，包括种群规模PSIZE、代沟GGAP和最大迭代次数MITER.

Step 5交叉算子对ζ(t)进行操作产生ζ1(t).

Step 6变异算子对ζ1(t)进行操作产生ζ2(t).

Step 7计算ζ2(t)中所有个体的适应度值，并执行选择算子对(Q∪ζ2(t))进行操作产生ζ(t+1).

Step 8判断迭代终止的条件，如果满足条件，则输出最优控制顶点，否则转到Step 5继续迭代.

4数值实验

例1以y=sin(x)作为采样函数，在区间[0,4π]上以0.2为间隔均匀取点和相应法向，取点个数为63，种群的规模取40，最大迭代次数为5 000，样条曲线次数为3.

例3以y=-(2x+1)e-10x2+2x-1作为采样函数,在区间[0,1]上以0.05为间隔均匀取点和相应法向,取点个数为20，种群规模取50,最大迭代次数为6 000,样条曲线次数为3.

选取了3个不同的实例(图2)，对所提出的算法的可行性进行了验证，每个实例均做10次相同实验，然后取均值并在表1～4中分别列出具体数值，所有数值乘以10-2为真实数值.从图3～8可以比较直观地看出：3个例子的实际收敛效果和拟合效果，实际证明笔者的算法对于解决此类问题是可行的.算法迭代的前期均能比较快速地收敛，但是对于后期随着种群越来越靠近最优值，收敛速度逐渐变慢，所以想获取更高的拟合精度就必须尽量延长算法的迭代次数.从表1～3中所列出的数据，比较鲜明地对比了3个实例对于控制点数量不同时，其实际拟合效果的不同.

实验结果对比了相同条件下取不同数量控制点时，数据点处以及法向处的误差对比，以及对比了笔者所采用节点向量跟其他两种经典节点向量取法的B样条曲线拟合效果.从数据中可以看出：当控制点的数量不同或者取不同的节点向量的时候均会影响到数据拟合误差的精度.除此之外，在表1～3中给出了笔者提出的方法与传统的最小二乘法[2]的实验数据对比.表1～3中数据误差1和法向误差1是利用笔者所提出的方法拟合所产生的实验数据，数据误差2和法向误差2是利用最小二乘法拟合所产生的实验数据.从三个例子总体来看，跟传统的最小二乘法相比，笔者所提方法在数据点误差项上略微处于劣势，但是相应数据点法向处的误差有比较明显的提高.

最后表4中给出了当控制点取相同数量时，利用笔者所提方法采用不同节点向量进行实验的实验数据.通过实验数据对比笔者发现也会对数据拟合存在影响.这里设置三种方案以方便比较，其中方案一采用2.2.1中所述的均匀节点向量；方案二采用2.2.2中所述的平均节点向量；方案三采用2.2.3中所述的皮格尔逼近节点向量.除节点向量选取不同，三种方案的其余实验条件均相同.方案一、二、三在表4中依次以编号1，2，3表示.通过实验数据对比，发现笔者方法中所采用的皮格尔逼近节点向量的拟合效果是最佳的.

图2　实验实例Fig.2　Test examples

图3　例1的GA收敛效果及其变量值分布图Fig.3　GA convergence effect and distribution of its variable values for example 1

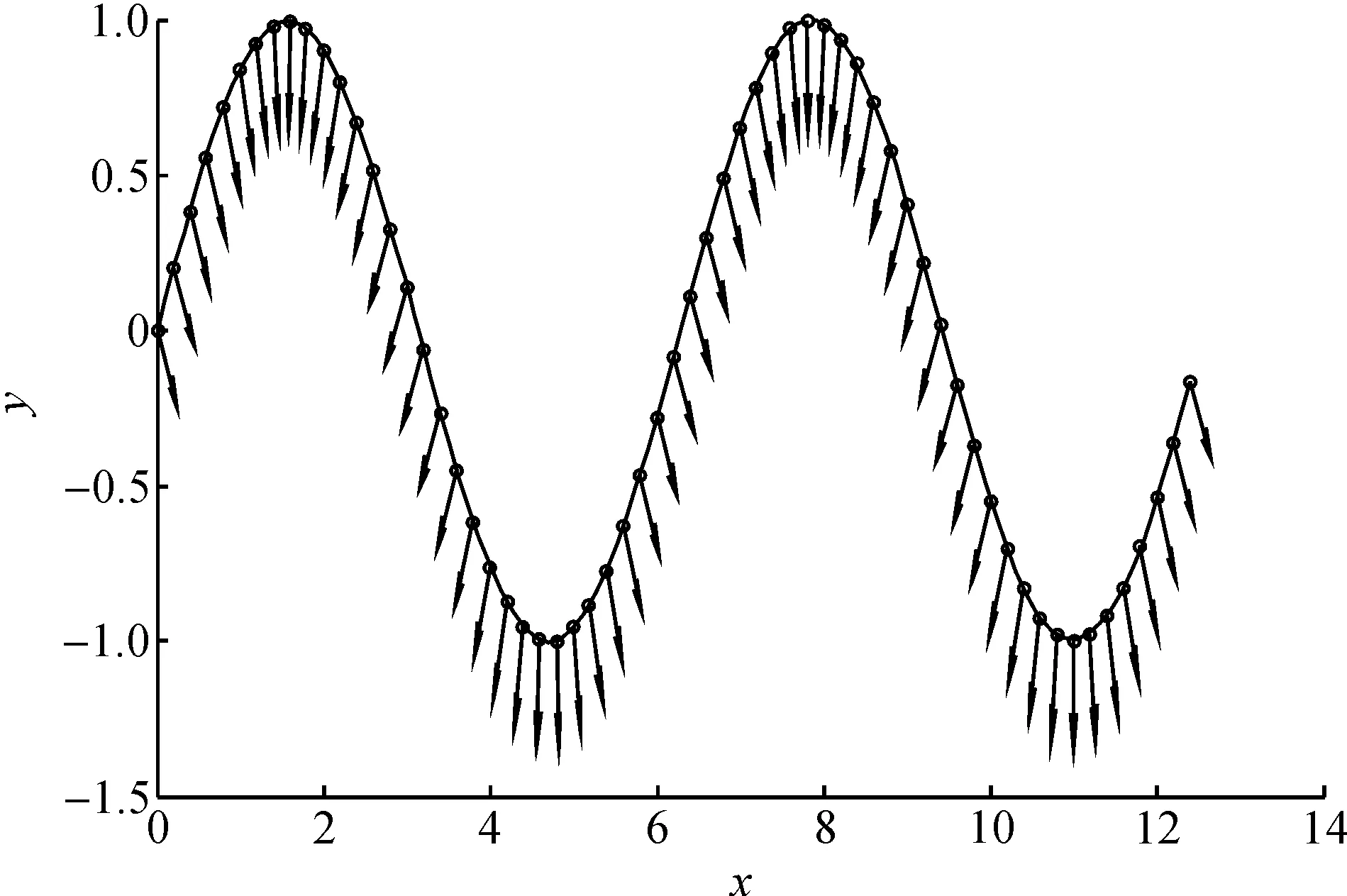
图4　例1基于GA的法向约束下B样条拟合效果图Fig.4　GA-based B-spline fitting with normal constraint for example 1

图5　例2的GA收敛效果及其变量值分布图Fig.5　GA convergence effect and distribution of its variable values for example 2

图6　例2基于GA的法向约束下B样条拟合效果图Fig.6　GA-based B-spline fitting with normal constraint for example 2

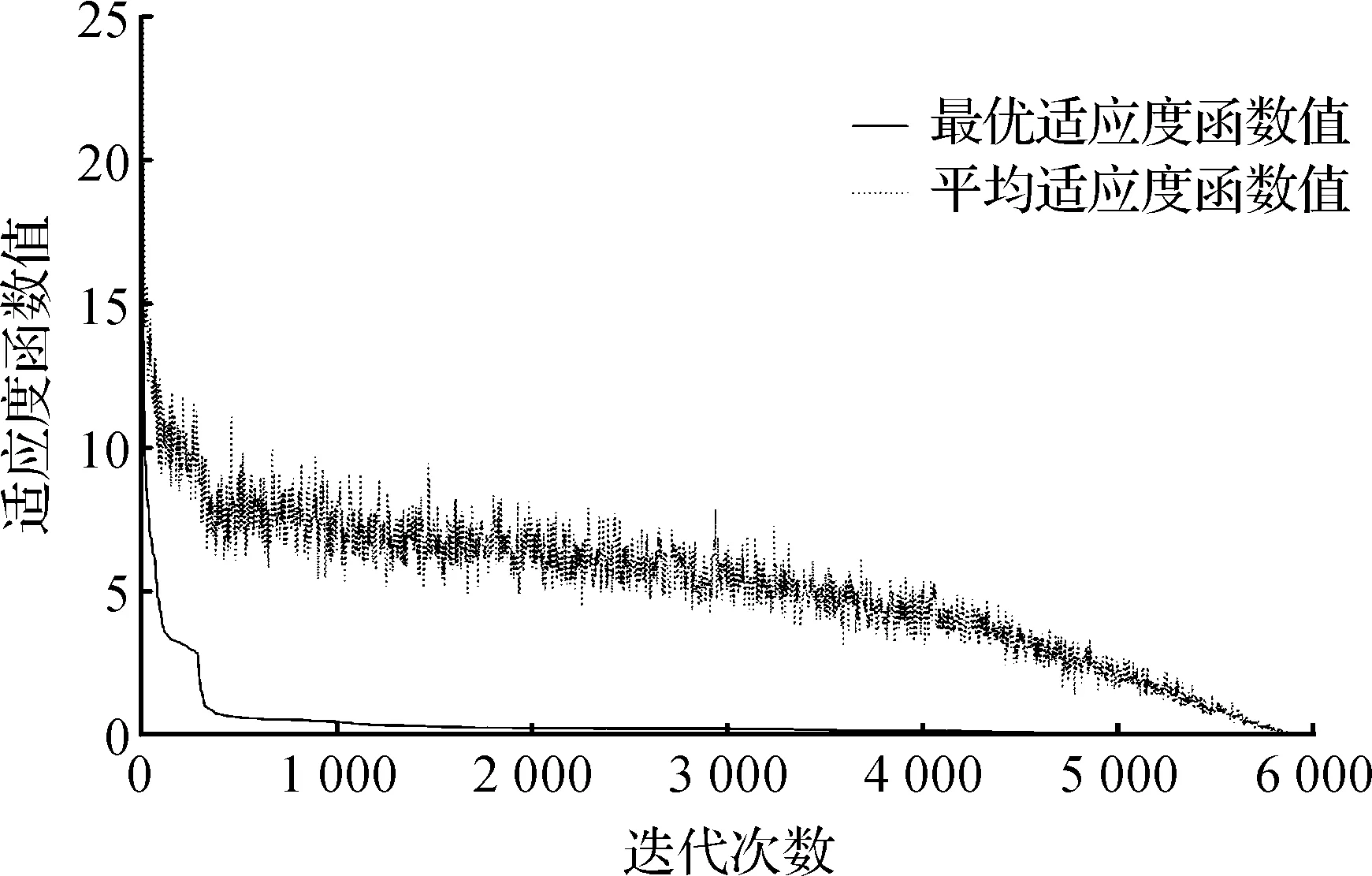
图7　例3的GA收敛效果及其变量值分布图Fig.7　GA convergence effect and distribution of its variable values for example 3

图8　例3基于GA的法向约束下B样条拟合效果图Fig.8　GA-based B-spline fitting with normal constraint for example 3

10-2

表2　例2控制点数量不同时的数据点和法向处的各自平均误差比较

表3　例3控制点数量不同时的数据点和法向处的各自平均误差比较

表4　测试例子在取不同的节点向量时数据点和法向处的各自平均误差比较

5结论

实验结果表明：提出的将有约束的数据拟合问题转化为无约束数据拟合的问题，然后使用遗传算法(GA)进行法向约束下曲线拟合的方案是可行的，但是要获取更高的数值精度, 就必须在收敛速度上作出牺牲，所以说未来工作的重点将在于如何提高收敛速度上.实验表明：所采取的节点向量对于样条曲线拟合问题确实比较有效，但是鉴于节点向量固定，所以不排除有更好的节点向量存在.另外，由于遗传算法随机盲选的特性，在求解该类问题的稳定性方面则欠佳.所以以上两点都是未来值得继续研究的问题.

参考文献：

[1]VARADY T, MARTIN R R, COX J. Reverse engineering of geometric models-an introduction[J].Computer-aided design，1997，29(4)：255-268.

[2]PIEGL L, TILLER W. The NURBS book[M]. New York：Springer-Verlag，1997.

[3]GOFUKU S, TAMURA S, MAEKAWA T. Point-tangent/point-normal B-spline curve interpolation by geometric algorithms[J]. Computer-aided design，2009，41(6)： 412-422.

[4]ABBAS A, NASRI A, MAEKAWA T. Generating B-spline

curves with points, normals and curvature constraints: a constructive approach[J]. The visual computer，2010，26(6)： 823-829.

[5]SHOICHI O, AHMAD N, LIN Hongwei, et al. Uniform B-spline curve interpolation with prescribed tangent and curvature vectors[J]. IEEE transactions on visualization and computer graphics,2012,18(9):1474-1487 .

[6]星蓉生，潘日晶.三次均匀B样条曲线插值数据点及其切矢的PIA算法[J].福建师范大学学报(自然科学版)，2014，30(1)：25-32.

[7]胡巧莉，寿华好.带法向约束的3次均匀B样条曲线插值[J].浙江大学学报(理学版)，2014，41(6)：619-623.

[8]YOSHIMOTO F, HARADA T, YOSHIMOTO Y. Data fitting with a spline using a real-coded genetic algorithm[J]. Computer-aided design，2003，35(8)： 751-760.

[9]ADI D I, SHAMSUDDIN S M, ALI A. Particle swarm optimization for nurbs curve fitting[C]//Proceedings of the 2009 Sixth International Conference on Computer Graphics, Imaging and Visualization. Tianjin: IEEE，2009：259-263.

[10]GALVEZ A, IGLESIAS A. Efficient particle swarm optimization approach for data fitting with free knot B-splines[J]. Computer-aided design，2011，43(12)：1683-1692.

[11]寿华好，黄永明，闫欣雅，等.两条代数曲线间Hausdorff距离的计算[J].浙江工业大学学报，2013，41(5)：574-577.

[12]寿华好，江瑜，缪永伟，等.平面代数曲线的PH-C曲线逼近[J].浙江工业大学学报，2012，40(1)：111-115.

[13]寿华好，高晖，闫欣雅，等.旋叶式压缩机气缸型线的设计[J].浙江工业大学学报，2014，42(6)：694-698.

(责任编辑：陈石平)

B-spline curve fitting algorithm for real-coded GA with normal constraint

SHOU Huahao, HU Liangchen

(College of Science, Zhejiang University of Technology, Hangzhou 310023, China)

Abstract:In this paper, genetic algorithm(GA) is applied to solve the problem of curve approximation with normal constraint. Firstly, the constrained problem is transformed to an unconstrained optimization problem. Then, the GA is used to replace the traditional equation solving method to obtain the optimal control point, and in order to achieve efficient approximation while it can simplify the calculation process and can be easy to be understood. Finally the curve approximations of this method under different knot vectors and different knots are compared. The experimental results show that the method is feasible to solve the problem of the B-spline curve approximation with normal constraint.

Keywords:discrete data; B-spline fitting; GA; normal constraint

收稿日期：2016-01-12

基金项目：国家自然科学基金资助项目(61572430，61272309，61472366)

作者简介：寿华好(1964―)，男，浙江诸暨人，教授，研究方向为计算机辅助几何设计与图形学，E-mail：shh@zjut.edu.cn.

中图分类号：TP391.7

文献标志码：A

文章编号：1006-4303(2016)04-0466-07