混凝土水渗透系数尺寸效应的试验研究

周欣竹，杨德蓝，郑建军,2

(1.浙江工业大学 建筑工程学院，浙江 杭州 310014；2.浙江省工程结构与防灾减灾技术研究重点实验室，浙江 杭州 310014)

混凝土水渗透系数尺寸效应的试验研究

周欣竹1,2,，杨德蓝1，郑建军1,2

(1.浙江工业大学 建筑工程学院，浙江 杭州 310014；2.浙江省工程结构与防灾减灾技术研究重点实验室，浙江 杭州 310014)

摘要：通过试验研究了混凝土水渗透系数的尺寸效应.试验中混凝土的水灰比为0.4，0.5，0.6，骨料体积率为55%，65%，75%，过水截面面积为0.008，0.015，0.025 m2.试验结果表明：对于给定水灰比和骨料体积率，混凝土水渗透系数随着过水截面面积的增大而增大，当过水截面面积达到0.015 m2时，水渗透系数趋于稳定.应用极值理论，分析了混凝土水渗透系数的尺寸效应，并根据试验结果，确定了Fréchet分布中的形状参数与骨料体积率和水灰比间的定量关系.

关键词：混凝土；水渗透系数；尺寸效应；Fréchet分布；形状参数

水渗透性在混凝土耐久性劣化中扮演极其重要的角色，是评价混凝土耐久性的重要指标和主要参数，影响混凝土水渗透性的主要因素包括孔隙率、孔径、水灰比、骨料体积率、骨料级配、外加剂和养护龄期等.赵铁军等通过MIP法测得混凝土的临界孔径和最可几孔径，其中临界孔径可以用来表征混凝土中孔隙的连通性和渗流路径的曲折性，对水渗透性的影响最为重要[1].陈凯明应用数值方法分析了孔隙形状对混凝土水渗透系数的影响，结果表明圆柱状孔具有最高的水渗透系数[2].Pereira等和Basheer等通过试验发现，粗骨料混凝土较细骨料混凝土具有更高的气渗透性[3-4].Zhao和郑书城等的试验结果表明混凝土水渗透性随着水灰比和骨料体积率的增大而增大[5-6].Grimmett指出：在细观水平上多孔介质存在一个渗流阀值[7]，当孔隙率大于渗流阀值时，孔隙与微裂缝相互连通形成渗流.Alarcon-Ruiz等根据Grimmett理论，采用类似于结构失效分析的最薄弱链条模型，认为混凝土的宏观渗透性可能取决于形成良好渗流通道的部分单元，混凝土的渗透性可能具有尺寸效应，并提出用Fréchet分布来预测混凝土渗透率[8].

在前人工作的基础上，采用稳定渗流法测定不同尺寸混凝土试件的水渗透系数，运用极值理论分析混凝土水渗透系数的尺寸效应，通过拟合确定Fréchet分布的形状参数，给出了形状参数与骨料体积率和水灰比之间的关系.

1试验材料与方法

1.1试验材料

本试验采用P·O 42.5普通硅酸盐水泥.粗骨料为碎石，表观密度为2 700 kg/m3，吸水率为1.13%，含水率为0.35%.细骨料为河砂，表观密度为2 650 kg/m3，吸水率为1.41%，含水率为0.35%.粗细骨料尺寸均服从富勒曲线，最大粒径为16 mm，最小粒径为0.30 mm.拌合用水为自来水.混凝土试件的配合比和组别如表1所示.

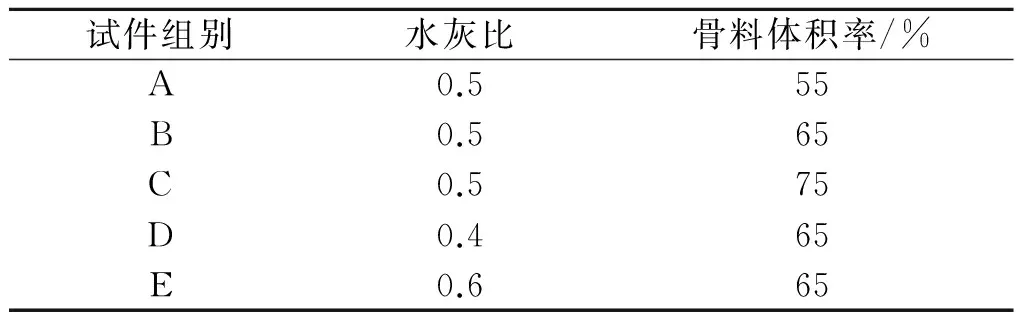
表1　混凝土配合比

1.2试验方法

混凝土试件为圆柱体，试件成型24 h后拆模，在标准养护室中养护28 d，再用混凝土切割机切去两端，取中间部分，对A至E组的混凝土配合比，制得尺寸为φ150 mm×50 mm，φ180 mm×50 mm和φ220 mm×50 mm的试件各3个，再进行统一编号，以A组为例，编号分别为A150，A180，A220.试件的上下表面为透水面，侧面用石蜡封闭.试验装置如图1所示，安装和测试步骤如下：

1) 将试件固定在渗透仪顶盖上，拧紧承台的固定螺母，翻转顶盖，倒扣于仪器主体上，拧紧顶盖的固定螺母使其与底座严格密封，完成组装.

2) 打开阀门2，通过入水口往渗透仪中注水直至阀门2有水溢出，关闭阀门2，连接进水管和水泵，调节水泵注水压力至2.0 MPa.

3) 打开阀门1，往阀门1下部空间中注满水，用橡皮管连接阀门1和移液管，保证移液管中有一定高度水柱，排空气泡，记录管中液面的初始读数，每隔4 h记录一次数据.当前后两次读数的增量趋于稳定时，可认为水的渗流已达到稳定状态，再记录3次读数.混凝土试件的水渗透系数可由达西定律计算：

(1)

式中：μ为水的运动粘性系数；Q为水的体积流量；L为试件厚度；A为试件的过水截面面积；ΔP为试件上下表面的水压差.

图1　混凝土水渗透试验装置示意Fig.1　Schematic of testing apparatus for water permeability of concrete

2试验结果分析

2.1试验结果

混凝土水渗透试验结果如表2所示，由于试件的上下表面压着同样大小的环形密封垫圈，各试件的过水断面面积S等于密封垫圈内径所对应的面积.

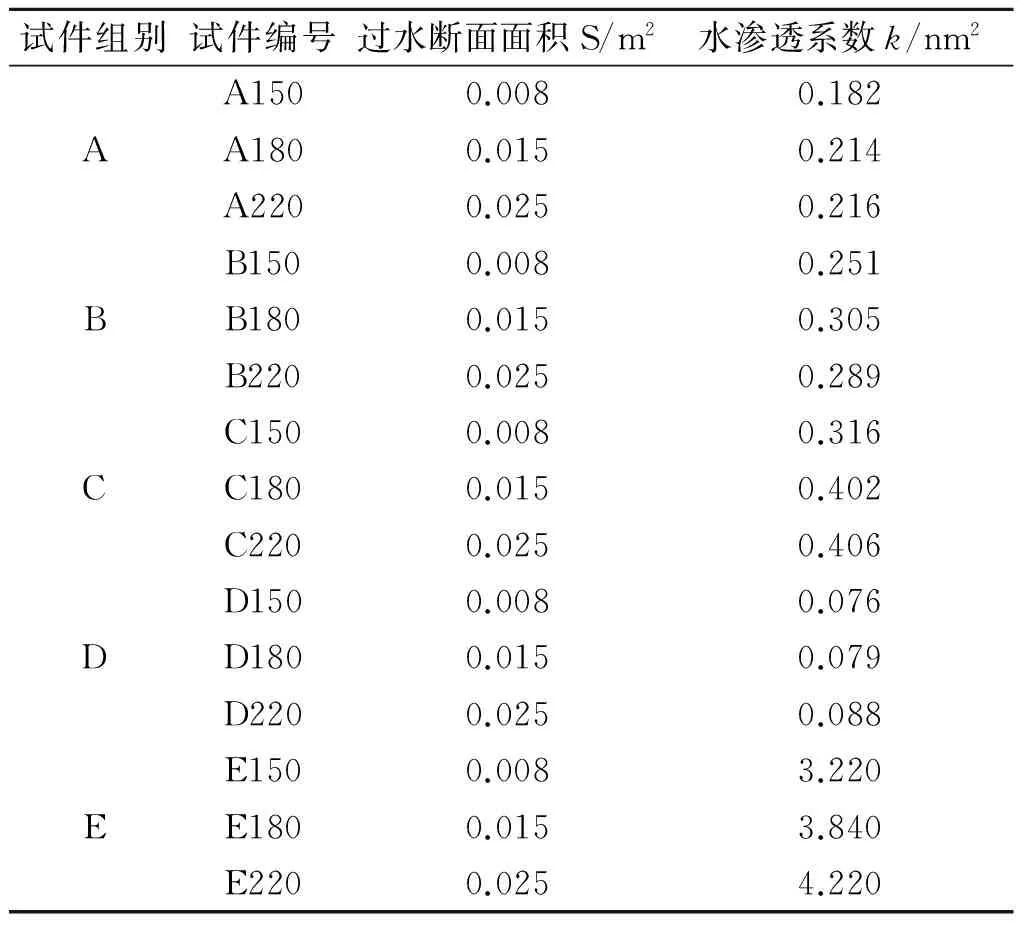
表2　混凝土水渗透系数

如果定义骨料体积率为每单位体积混凝土中的骨料体积，则混凝土水渗透系数k与骨料体积率Va和水灰比w/c之间的关系分别如图2，3所示.从图2可以看出：混凝土水渗透系数随骨料体积率的增大而增大，这是由于混凝土是一种由骨料、水泥石和界面组成的三相复合材料，相比于水泥石和界面，骨料几乎是不可渗透的，水泥石中含有凝胶孔和毛细孔，但它们的孔径远小于界面层的孔径，因此，水渗透主要取决于界面[9].根据Zheng和Zhou的结论[10]，当骨料体积率为55%时，相邻骨料的界面层相互连通而形成渗流，骨料体积率越大，界面体积率也越大，水渗透系数也越大.从图3可以看出：混凝土水渗透系数先随着水灰比的增大而缓慢增大，当水灰比大于0.5时，随着水灰比的增大而急剧增大，这是因为随着水灰比的增大，孔隙率和孔径均增大，大大提高了孔隙的连通性，这与Neville的结论类似[11]，即当孔隙率从10%增加到25%时，水渗透系数增大较慢，而当孔隙率从25%增加到40%时，水渗透系数出现了较大幅度的增大，也说明了试验结果的可靠性.

图2　水渗透系数和骨料体积率的关系Fig.2　Relationship between water permeability and aggregate volume fraction

图3　水渗透系数和水灰比的关系Fig.3　Relationship between water permeability and water/cement ratio

当水灰比为0.5时，混凝土水渗透系数与过水截面面积S之间的关系如图4所示.从图4可以看出：水渗透系数随着S的增大而增大，当S达到0.015 m2时，水渗透系数增大的速率减慢并逐渐趋于稳定.对于水灰比为0.4和0.6的混凝土，可以得到类似的结论.根据Alarcon-Ruiz等的解释[8]，水渗透系数随尺寸变化的原因可能是由于混凝土试件尺寸越大，存在更大渗流通道的概率越高，而更大的渗流通道对混凝土的水渗透起决定作用.

图4　水渗透系数和过水截面面积的关系Fig.4　Relationship between water permeability and cross-sectional area

2.1极值理论分析

区间最值模型是一种较为经典的极值理论，它建立在大量独立抽样区间中的最大和最小观察值的基础上.设X1，X2，…，Xn为服从分布F(X)的n个独立样本，定义Xmax=max(X1,X2,…,Xn)，则其分布函数为

P(Xmax≤x)=(F(x))n

(2)

根据Ficher-Trippett定理，F(x)必收敛于如下三种分布之一：Gumbel分布、Fréchet分布和Weibull分布.这三种极大值分布有很大的区别，实际应用时应合理选择.Alarcon-Ruiz等认为[8]：混凝土的渗透率可能取决于形成良好渗流通道的部分单元，即渗透率较大的单元，且这部分单元对混凝土的整体渗透率起决定性的作用，混凝土渗透试验中所测得的宏观渗透率远小于微小单元渗透率的极大值.因此，可认为微小单元渗透率极大值分布是无界的，采用Fréchet分布来分析混凝土单元的渗透率极大值分布是合理的.Fréchet分布的数学表达式为

(3)

式中：α为形状参数，反映含有连通微裂缝和连通孔隙等混凝土单元的渗透率分布，对于不同的α值，Fréchet分布曲线如图5所示.从图5可以看出：对于给定的x值，F(x)随着α的减小而减小，表明α越小，渗透率分布越分散，尺寸效应越明显.

图5　不同α值的Fréchet分布曲线Fig.5　Fréchet’s distribution curves for different α values

根据上述假设，可以将混凝土各单元的渗透率看成n个独立同分布的随机变量K1，K2，…，Kn，单元数n与试件的过水截面面积S成正比.利用式(3)对式(2)进行变换，有

log(P(Kmax≤k))=nlog(F(k))=μS(-k-α)

(4)

Sk-α=η

(5)

式中η为正数.最后，水渗透系数k与过水截面面积S的关系为

k=γS1/α

(6)

式中γ=η-1/α.利用式(6)对表2中的A组至E组混凝土的试验数据进行拟合，获得指数参数1/α与骨料体积率和水灰比的关系，结果如图6，7所示.从图6可以得出：可能由于试验误差的原因，骨料体积率为65%的混凝土水渗透系数比骨料体积率为55%的混凝土水渗透系数略小，但从整体上看，1/α随着骨料体积率的增大而增大，这是因为骨料体积率越大，出现微裂缝、较大渗流通道的概率越大，α越小，1/α越大，混凝土水渗透系数的尺寸效应越明显.从图7可以看出：1/α先随着水灰比的增大而缓慢增大，当水灰比大于0.5时，1/α随水灰比的增大而急剧增大，这是因为水灰比越大，水泥浆体孔隙率越大，而且当水灰比大于0.5时，相邻骨料的界面相互连通，出现较大渗流通道的概率越大，α越小，1/α越大，混凝土水渗透系数的尺寸效应也越明显.

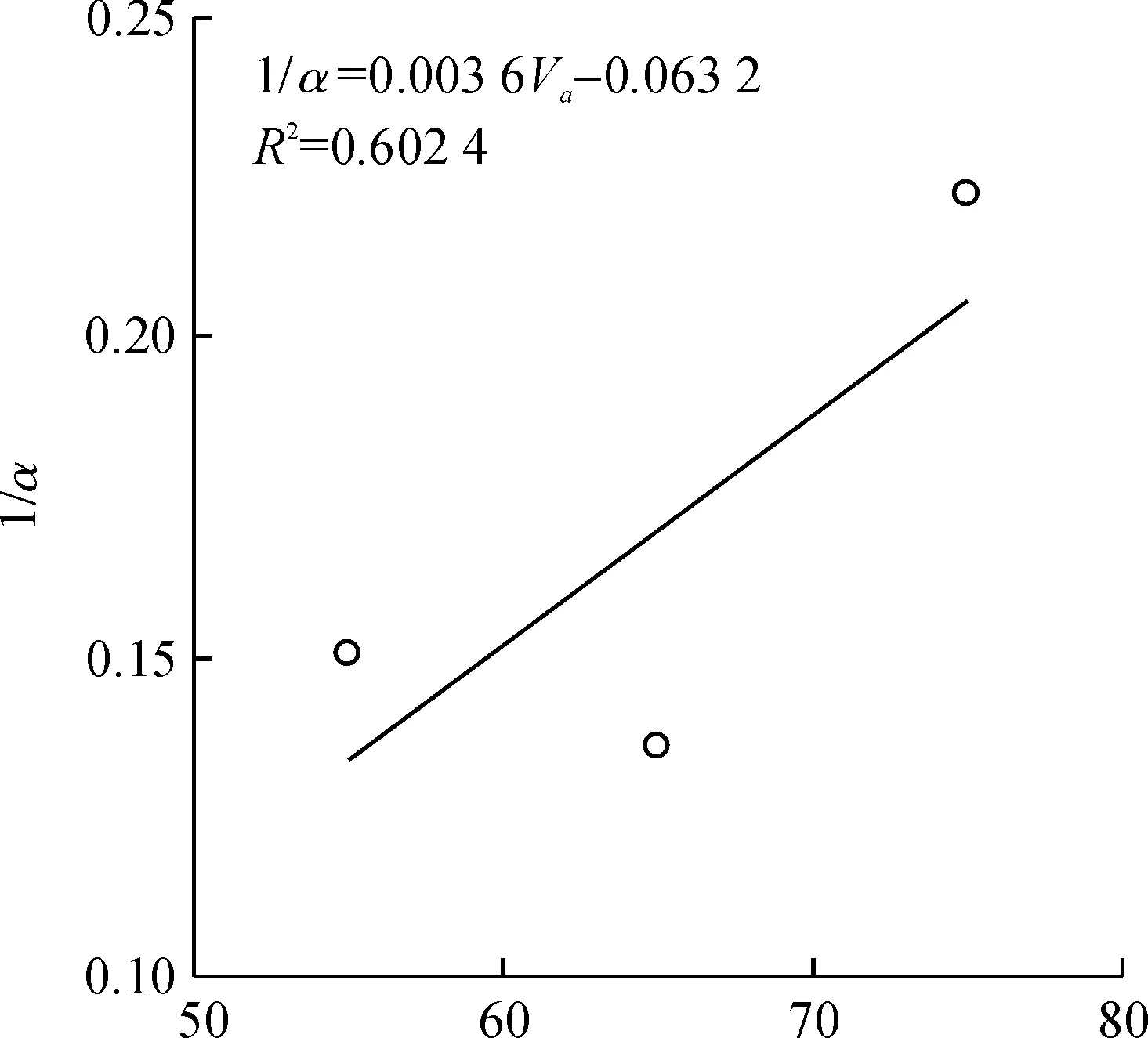
图6　形状参数与骨料体积率的关系Fig.6　Relationship between shape parameter and aggregate volume fraction

图7　形状参数与水灰比的关系Fig.7　Relationship between shape parameter and water/cement ratio

4结论

由于混凝土渗透性试验难度大、周期长，要获得大量的试验数据非常困难.又由于笔者所给出的试验数据有限，对结果进行线性拟合分析也只能说是定性的，所得结论只具有参考价值，要得到比较精确的定量分析结果，需要对现有的试验方法和试验仪器进行改正，这是将来研究的重点之一.实验室试验和理论分析的结果表明：对于给定的水灰比和骨料体积率，混凝土水渗透系数随着过水截面面积的增大而增大，但增大速率逐渐减小；极值理论可以较好地分析混凝土水渗透系数的尺寸效应，混凝土单元的水渗透系数符合Fréchet分布，该分布所包含的形状参数随着骨料体积率和水灰比的增大而增大.

参考文献：

[1]赵铁军,朱金铨,冯乃谦.混凝土孔隙分析中的表征参数[C]//阎培渝,姚燕.全国水泥基复合材料科学与技术.北京:中国建材工业出版社,1999:5-11.

[2]陈凯明.混凝土水渗透性评价的数值方法[D].杭州:浙江工业大学,2013.

[3]PEREIRA C G, CASTRO-GOMES J, de OLIVEIRA L P. Influence of natural coarse aggregate size, mineralogy and water content on the permeability of structural concrete[J]. Construction and building materials,2009,23(2):602-608.

[4]BASHEER L, BASHEER P A M, LONG A E. Influence of coarse aggregate on the permeation durability and the microstructure characteristics of ordinary Portland cement concrete[J]. Construction and building materials,2005,19(9):682-690.

[5]赵铁军,周宗辉,迟培云.水胶比、掺和料和龄期对混凝土渗透性的影响[J].混凝土,1998(2):19-22.

[6]郑书城,郑建军.混凝土水渗透性试验研究和影响因素分析[J].混凝土,2011(5):10-12.

[7]GRIMMETT G. Percolation[M]. Berlin: Springer-Verlag,1989.

[8]ALARCON-RUIZ L, BROCATO M, PONT S D, et al. Size effect in concrete intrinsic permeability measurements[J]. Transport in porous media,2010,85(2):544-546.

[9]GARBOCZI E J, BENTZ D P. Modelling of the microstructure and transport properties of concrete[J]. Construction and building materials,1996,10(5):293-300.

[10]ZHENG Jianjun, ZHOU Xinzhu. Percolation of ITZs in concrete and effects of attributing factors[J]. Journal of materials in civil engineering,2007,19(9):784-790.

[11]NEVILLE A M. Properties of concrete[M]. Harlow: Person Education Limited,1995.

(责任编辑：陈石平)

An experimental study on size effect on water permeability of concrete

ZHOU Xinzhu1,2, YANG Delan1, ZHENG Jianjun1,2

(1.College of Civil Engineering and Architecture, Zhejiang University of Technology, Hangzhou 310014, China;2.Zhejiang Key Laboratory of Civil Engineering Structures & Disaster Prevention and Mitigation Technology, Hangzhou 310014, China)

Abstract:The size effect on the water permeability of concrete is studied through experiment. In this test, the adopted concretes have water/cement ratios of 0.4, 0.5, and 0.6, aggregate volume fractions of 55%, 65%, and 75%, and cross-sectional areas of 0.008, 0.015, and 0.025 m2, respectively. The test results show that, for a given water/cement ratio and an aggregate volume fraction, the water permeability of concrete increases with the increase of the cross-sectional area. When the cross-sectional area reaches 0.015 m2, the water permeability tends to be stable. The extreme value theory is used to analyze the size effect on the water permeability of concrete. Based on the test results, the quantitative relationships between the shape parameter in the Fréchet distribution, and the aggregate volume fraction and the water/cement ratio are determined.

Keywords:concrete; water permeability; size effect; Fréchet distribution; shape parameter

收稿日期：2016-01-25

基金项目：国家自然科学基金资助项目(51379188)；浙江省自然科学基金资助项目(LY15E090006)

作者简介：周欣竹(1966—)，女，江苏南京人，教授，研究方向为混凝土材料与结构耐久性，E-mail：xzzhou66@zjut.edu.cn.

中图分类号：TU57

文献标志码：A

文章编号：1006-4303(2016)04-0435-04