妙用变换巧解题

姜奎宏

摘 要：几何问题主要考察了学生们的思维变换能力。有些几何问题在不经图形变换的情况下很难解答，但往往通过简单的图形平移、旋转等变换就很容易得到问题的答案。利用图形变换解题的技巧也已经成为几何题目的重要考察点。

关键词：几何问题；变换；新图形；解题技巧

有些几何问题初看很难入手，但当把图形的某一部分或平移、或旋转、或翻折等变换后，便可将分散的条件相对集中，发现新图形的一些奇妙性质，解题思路也就随之畅通。请看下面几个例子：

例1.在平行四边形ABCD中，点A1，A2，A3，A4和C1，C2，C3，C4分别为AB和CD的五等分点，点B1，B2和D1，D2分别是BC和DA的三等分点，已知四边形A4B2C4D2的面积为1，则平行四边形ABCD面积为（ ）

A.2 B.35 C.53 D.15

分析：此题根据面积公式无法直接计算，注意到A4D2，B2C4，A4B2 D2C4，故可考虑将△AA4D2平移与△CB2C4拼接，△BA4B2平移与△DD2C4拼接，也可将阴影部分四边形A4B2C4D2先分割、再平移拼接，这样图中阴影部分与的ABCD面积关系便一目了然。

解：将阴影部分四边形A4B2C4D2分割，平移

可知S四边形A4B2C4D2=SABCD

∴SABCD =×1 =

故选（C）

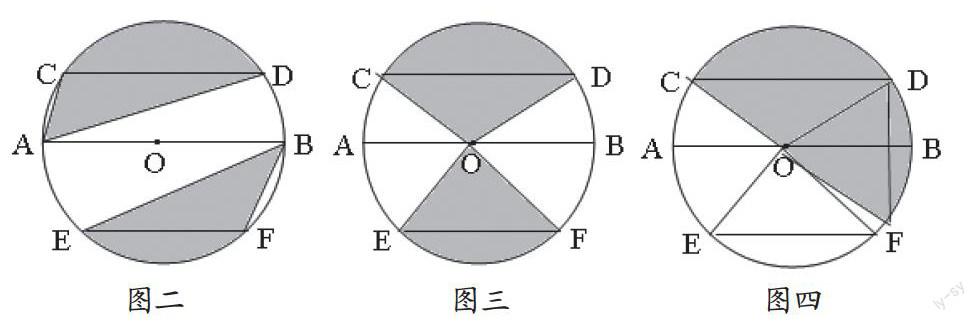
例2.如图2，AB是⊙O的直径，CD、EF是⊙O的弦，且AB∥CD，AB∥EF，AB=10，CD=8，EF=6，求图中阴影部分面积。

分析：根据条件，运用有关面积计算公式直接计算阴影部分面积有困难。注意到AB∥CD，AB∥EF，于是图中阴影部分面积可先考虑等积变换转化为扇形OCD、扇形OEF的面积（如图3），再将扇形OEF通过旋转变换至图4位置，问题便迎刀而解。

解：连结 OC、OD，OE、OF

∵ AB∥CD，AB∥EF

∴ S扇形OCD=S阴影CAD

S扇形OEF=S阴影BEF

∴S阴影= S扇形OCD+ S扇形OEF

将扇形EOF绕点0按逆时针方向旋转，使OF与0D重合

由题设条件AB=10，CD=8，EF=6

故旋转后的两个扇形恰好构成一个半圆（如图4）

∴ S阴影=S⊙O=π

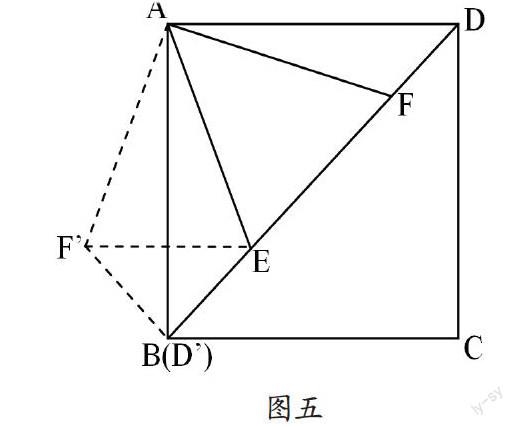
例3.如图 5，正方形 ABCD 中，∠EAF=45°，AE、AF 交 BD 于 E、F，求证：BE2+DF2=EF2

分析：由结论可知三条线段为一直角 三角形的三边长，但图中三条线段在同一直线上，故考虑用旋转变换方法 构造新的图形来证题。

证明：将△AFD绕A点顺时针旋转90°得△AF'B，连F'E，

则AF'=AF

F'B=FD

∠F'AB=∠FAD

∵∠EAF=45°，∠BAD=90°

∴∠FAD+∠BAE=45°

∴∠F'AB+∠BAE=45°

即∠F'AE=45°

∴∠F'AE=∠FAE

∴△AF'E≌△AFE

∴F'E=EF

∵∠F'BA=∠ADF=∠ABE=45°

∴∠F'BE=90°

∴BE2+F'B2=EF'2

∴BE2+DF2=EF2

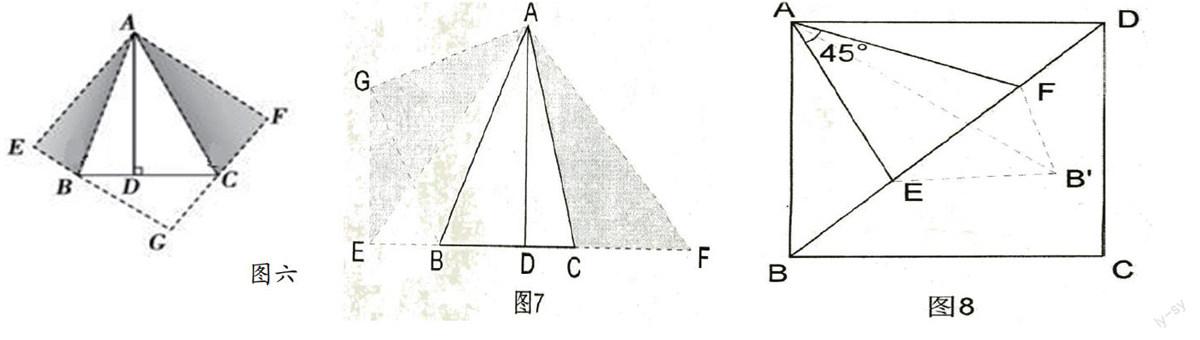
例4.如图，在△ABC中，∠BAC=45°，AD⊥BC于D，BD=3，DC=2，求AD。

分析：本题想从已知条件直接求出此三角形的面积确实有些困难，如果从题设∠BAC=45°，AD⊥BC出发，可以捕捉到利用轴对称性质构造一个正方形的信息，那么问题立即可以获解。

解：如图6，将△ABD沿AB翻折180°得Rt△ABE，将Rt△ACD沿AC翻折180°，得Rt△ACF，延长EB，FC交于G。

在四边形AEGF中，∵∠EAF=∠E=∠F=90°

AE=AF=AD

∴四边形AEGF为正方形

∵∠G=90°

EG=FG=AD

令AD=x，则BG=EG-EB=x-3

CG=FG-FC=x-2

于是在Rt△GBC中，由勾股定理（x-3）2+（x-2）2=52

整理得x2-5x-6=0

∴x1=-1（舍去），x2=6

即AD=6

說明：（1）本题另一解法如图7：先将△ABC补成等腰Rt△AEF，然后将△ACF绕点A顺时针旋转至△AGE的位置，在Rt△BEG中，应用勾股定理便可得其解（过程略）。

（2）例3也可以采用翻折的方法，如图8，将△ABE沿直线AE翻折180°得△AB'E，连接B'F，同样可得结论（证明过程略）。

几何问题往往是巧妙的，让图形“动”起来是研究图形的好方法。在证明和求值的诸多几何问题中，如果不能直接找到解题的突破口，我们就要另辟蹊径，细心观察图形，抓住一些重要的条件（例如：线段和角度），借助图形变换巧解题，从而化复杂为简洁，化不规则图形为规则图形。