改进层次分析法在配网线路防雷评估中的应用*

刘刚　马浩禹　张弦

(1.华南理工大学 电力学院， 广东 广州 510640； 2．国网湖南电力公司检修公司， 湖南 长沙 410000)

改进层次分析法在配网线路防雷评估中的应用*

刘刚1马浩禹1张弦2

(1.华南理工大学 电力学院， 广东 广州 510640； 2．国网湖南电力公司检修公司， 湖南 长沙 410000)

摘要:为了有效减少输电线路雷击事故，确保电力系统的安全，电力运行部门必须采取一定的防雷措施来提高输电线路的耐雷水平.文中基于采用新标度的层次分析法和模糊综合评价法，综合考虑降低跳闸率、工程费用、效果目标、维护难易度、运行寿命等因素的影响，构建了一个适用于配电网的防雷措施评估模型，并对实际线路防雷措施进行评估.根据层次分析法得到各防雷措施相对于目标层的权重值，然后采用模糊综合评价法得到各改造方案的隶属度，从而确定线路最优化的改造方案.结果表明，该评估系统能够有效地对配电线路进行评估，确定配电线路最优防雷措施及线路改造方案.

关键词：防雷；改进层次分析法；模糊综合评价；新标度；效果评估

雷击事故在输电线路故障中一直占据很大的比例.广东电网线路防雷运行数据表明，广东某地区10 kV输电线路2012年雷击跳闸119次，占线路总跳闸次数的15%，2013年雷击跳闸116次，占线路总跳闸次数的20.1%.配网雷击事故不容小觑，建立一个切实可行的防雷评估系统对配网输电线路的防雷改造具有重要的指导意义.

目前，国际上评估线路耐雷水平的方法有规程法、行波法、电气几何模型法[1]及先导发展模型法[2]等，层次分析法[3]现也被应用到防雷评估中.张志劲等[4]采用1-9标度法对输电线路进行防雷评估，赵淳等[5]提出用0-2三标度法代替1-9标度法.标度的选取直接影响到防雷评估的精确性，对标度选取的研究成为层次分析法应用于防雷评估的研究重点.

文中运用层次分析法，采用精确度更高的10/10-18/2标度对配网防雷措施进行评估，并通过模糊综合评价法对输电线路进行等级评价，得出最优的输电线路防雷改造方案.

1层次分析法

1.1步骤

层次分析法的过程可用图1表示.

图1　层次分析法流程图

(1)建立层次结构模型.通过对实际问题的分析，将问题分解为若干个因素，按照不同属性再分成目标层、准则层、方案层等不同的层次，同一层的各个因素影响上一层的因素.建立结构层次从上而下依次为目标层、准则层和方案层，使复杂的问题条理化、层次化.

(2)构造判断矩阵.从准则层开始，对影响上一层每个因素的同一层的各个因素进行两两的重要性比较，得出对比值，直到最下层，构成多个判断矩阵.

(3)计算权向量并作一致性检验.求解每一个判断矩阵的最大特征根及其归一化的特征向量，并做一致性检验.若检验通过，特征向量即为权向量；若不通过，需重新构造判断矩阵，直至构造出能通过一致性检验的矩阵.

(4)计算各个方案对于目标层的合成权重并进行一致性检验，对每个方案对于目标层的相对重要性进行总排序从而确定最优方案.

在层次分析法中进行各个因素两两间相对重要性的比较时，存在着一定的人为主观因素，而且当每层因素过多时计算繁琐.因此，在运用层次分析法时，首先要对每层的因素进行一个初选，保证构建出来的模型不至于过于复杂，有利于计算.

1.2比例标度的选取

现有的标度有1-9标度、0-1标度、0-2标度、0.1-0.9标度、9/9-9/1标度、10/10-18/2标度和指数标度[6- 8].

1-9标度简单明了，但文献[9]指出,1-9标度与人们理想的期望值偏差较大，可能对权重值的计算造成比较大的误差.0-1标度法和0-2标度法均为三标度法，其标度值相对于其他标度来说较少，可以降低人的主观因素作用，但是由于其过分地简化，加上要进行复杂的数学变换，容易造成原始信息不足或遗失，不适用于比较复杂的系统.0.1-0.9标度对于排序有一定的价值，但同样不能够比较精确地反映实际情况[10].

侯岳衡等[11]对1-9标度、9/9-9/1标度、10/10-18/2标度和指数标度这4个标度进行了比较并做出了评价分析.表1为4种标度的取值.

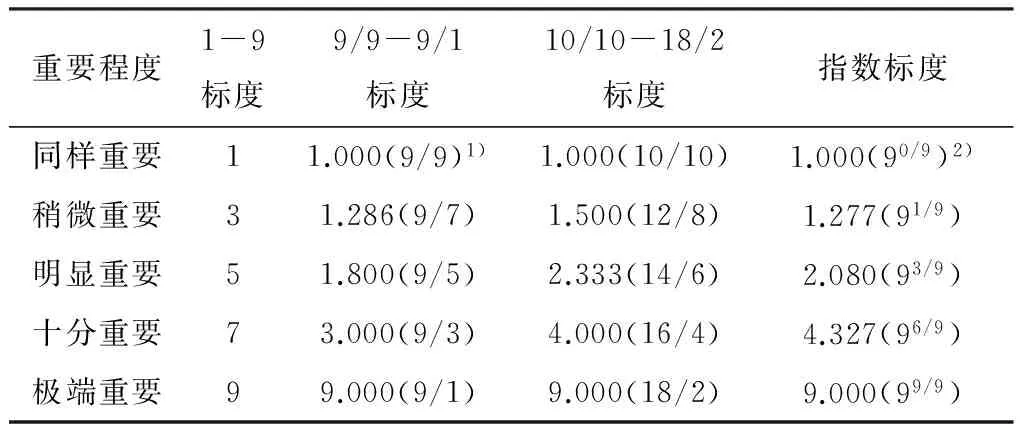
表1　4种标度取值比较

1)标度值(标度)；2)指数标度值(指数标度)

根据表1中各标度的取值，对4种标度建立判断矩阵，求它们各自的权值并作一致性比较，求出的权值符合程度比较好，并且一致性高的标度比较好.

分析得到的4种标度的性能如表2所示.

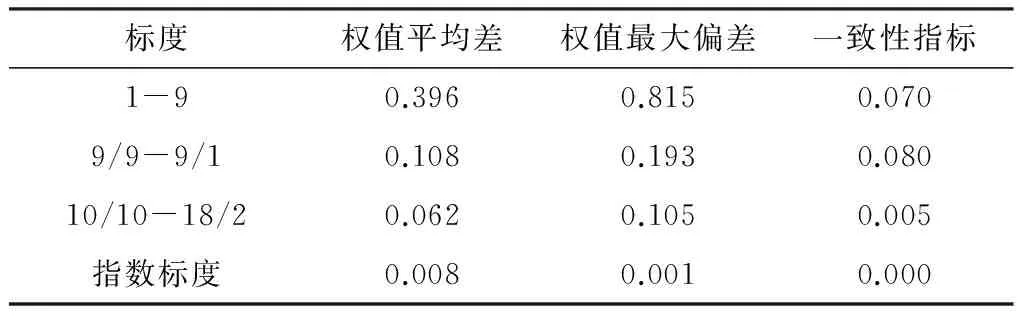
表2　不同标度性能的比较

表2对这4个标度的权值平均差、权值最大偏差以及一致性指标CI进行比较，得出指数标度性能最好、10/10-18/2标度次之的结论.由于指数标度在构造判断矩阵及进行计算时过程繁琐，标度值也不容易记住，从精确度及实用性综合考虑，选择10/10-18/2标度在应用中更为方便.因此，文中采用了10/10-18/2标度法.

2层次分析法在配网防雷措施评估中的应用

配网具有多种防雷措施，在根据线路实际情况选择合适的防雷措施时必须考虑诸多因素，需要一个切实可行的选择方法.运用层次分析法能够构建一个简单明了的配网防雷评估系统，对配网防雷措施进行快速、有效的选择.

2.1防雷评估模型的建立

(1)目标层.这一层次中只有一个元素，即根据配网输电线路防雷措施的特点以及线路改造的要求，确定最优的改造措施.

(2)准则层.准则层包括实现目标层所必须考虑的因素.根据实际工程的应用以及防雷效果的考虑，确定配网输电线路防雷措施的准则层因素有：降低跳闸率、工程费用、效果目标、维护难易度和运行寿命.

(3)方案层.方案层是基于配网防雷特点选取的防雷措施.通过对配网已有防雷措施及其各自特点的分析，确定方案层的措施包括降低杆塔接地电阻、安装避雷器、差绝缘、架设避雷线和安装防雷间隙.

建立防雷措施评估模型如图2所示.

2.2防雷评估中的层次分析法

(1)根据已经构建好的防雷评估模型，将各防雷措施方案层相对于准则层的比较矩阵记为A1，A2，…，A5，准则层各因素相对于目标层的比较矩阵记为 B.其中，A1，A2，…，A5为5×5阶比较矩阵，矩阵中元素a1ij，a2ij，…，a5ij为第i种措施相对于第j种措施关于准则层某一因素的重要性比值.B为一个5×5阶对比矩阵，bij为第i个准则相对于第j个准则关于目标层的重要性比值.

图2　配网防雷评估模型

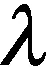
(1)

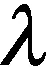
将求得的一致性指标CI与随机一致性指标RI进行比较，定义随机性一致性比率：

(2)

当CR<0.1时，说明比较矩阵具有满意的一致性，可以接受，否则就必须调整比较矩阵，直到有满意的一致性为止.

文献[12]中给出了10/10-18/2标度不同阶数的RI值，如表3所示.

表3　10/10-18/2标度不同阶数的RI值

判断矩阵权重值可用特征向量法计算得到：

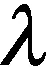
(3)

式中，A为判断矩阵.算出判断矩阵的权向量w，并进行归一化，得出的权向量w即为同一层因素相对于上一层某因素相对重要性的排序权值.

(3)计算组合权向量.

根据

(4)

求出各防雷措施相对于准则层某一因素的重要性与该因素相对于目标重要性的乘积的和，即可得到该防雷措施对于目标的重要性.通过总权值的排序W(w1,w2,w3,w4,w5)即可得出最佳的防雷措施.

式(4)中，wi为总权值归一化向量W中的因素，wj(a)i为各方案层对于准则层归一化权向量中的因素，wj(b)为准则层对于目标层归一化权向量中的因素.

3模糊综合评价法

3.1原理

模糊综合评价法用模糊数学对受到多种因素制约的事物或对象做出一个总体的评价.防雷评估中，通常会存在一些分类标准不明确、边界不清楚的模糊现象，因此在此类研究中引入模糊综合评价法，可更为客观准确地反映各种指标的特性，降低主观因素的影响，进而提高评估效果[13].

3.2步骤

(1)确定m个评价因素和n个评价等级.设论域U是m个评价因素的集合：

U={u1,u2,…,um}

(5)

设论域V是n个评价等级的集合：

V={v1,v2,…,vn}

(6)

(2)确定评价等级论域V

根据防雷保护改造的特点，可将防雷评估等级论域V定义为

V={差，一般，好，较好，非常好}.

由于评价等级V在一定程度上具有模糊性，因此在评价时将各评价等级的取值进行模糊化，从而可以得到与评价论域V相对应的取值论域Ω,

Ω={0-2,2-4,4-6,6-8,8-10}.

(3)确定评价因素集合U的隶属函数u(x)

在实际应用中，三角隶属函数相对其他隶属函数而言，受数据类型影响较小，应用于防雷评估中更为客观.根据最大隶属度原则，构造如下隶属函数[14]:

(7)

(8)

(9)

(10)

(11)

式中，u1(x)，u2(x),…,u5(x)表示隶属于评价等级Ω的隶属函数,x的值为实际权重值对应的等级值.

(4)构建模糊关系矩阵F

将U、V中任意元素搭配(ui,vj)构成n个评价因素下的笛卡儿乘积，并将(ui,vj)记为fij,表示评价因素u对评价等级v的隶属度，由此可构造一个m×n阶的评价矩阵F:

(12)

(5)综合评价的确定

根据评价矩阵F与层次分析法得到的权重矢量W计算得出模糊综合评价的隶属度矢量ξ，可表示为

ζ=W○F=[ζ1ζ2…ζm]

(13)

式中，○ 表示合成算子.在模糊计算中，合成算子有多种类型，比如M(︿,﹀ )，M(·,︿ )，M(︿,⊙)和M(·,⊙).其中，M(·,⊙)型为加权平均型，能明显体现出权数作用，综合程度较高，能充分利用提供的信息，因此选用此模型作为合成算子进行计算.

根据最大隶属原则，可认为ζi=max{ζ1,ζ2,…,ζm}为该种因素的第i等级，从而得出该种方案的评价等级.

4应用结果及分析

根据工程要求及多年运行经验，对配网防雷措施评估模型各层重要性取值如表4、5所示.

表4　准则层各因素重要性取值

表5　方案层各因素重要性取值

采用Matlab对构造出的矩阵进行计算，可得各层的归一化权向量值.

W=(0.354 3,0.248 7,0.199 8,0.083 2,0.114 1).

W=(0.116 4,0.467 0,0.073 1,0.293 2,0.050 3).

W=(0.389 9,0.091 1,0.210 0,0.047 4,0.267 1).

W=(0.096 1,0.377 9,0.065 4,0.189 5,0.271 2).

W=(0.402 7,0.107 3,0.077 7,0.258 6,0.153 8).

W=(0.309 2,0.152 5,0.072 2,0.365 6,0.100 4).

根据式(4)可得到方案层相对于目标层的权重值为W=(0.226 2,0.289 9,0.105 9,0.216 8,0.162 7).因此可得到配电网输电线路防雷措施方案的优先顺序为：安装避雷器、降低杆塔接地电阻、架设避雷线、安装防雷间隙、差绝缘.

采用模糊综合评价法进行等级评估时，评价论域取值为0-10，与用层次分析法计算出的权重形式不相符合，难以进行分析计算.为了便于分析，可采用插值法对论域进行数值转换.得到的评价等级论域对应权重值如表6所示.

表6　评价等级对应值

选取广东电网某10 kV配电网输电线路某段均安装了降低杆塔接地电阻、避雷器、差绝缘、避雷线和防雷间隙5种防雷措施的杆塔为研究对象进行分析，分别记为杆塔#1-#6.由前文可得理想情况下5种防雷措施的权重值为

W=(0.226 2,0.289 9,0.105 9,0.216 8,0.162 7).

由于防雷措施安装情况、工作环境以及运行年限等的不同，不同杆塔的同种防雷措施的权重取值也不相同.根据工作人员经验及实际运行情况，采用层次分析法对上述杆塔各防雷措施的实际权重值取值如表7所示.

表7　各防雷措施的权重值

综合评价时的论域转换值如表8所示.

表8　实际权重值在论域中的对应值

经过计算得到各杆塔防雷措施隶属度(如表9所示).

表9各防雷措施的隶属度及评价等级

Table 9Memberships and the corresponding levels of lighting protection measures

杆塔号数隶属度最大隶属度评价等级#1ξ=(0.0743,0.5096,0.1277,0.1426,0.1474)ξ2=0.5096一般#2ξ=(0.2097,0.2757,0.0168,0.4961,0.0031)ξ4=0.4961好#3ξ=(0.0008,0.5988,0.2790,0.1230,0)ξ2=0.5988一般#4ξ=(0.1250,0.3595,0.1959,0.3155,0.0056)ξ2=0.3595一般#5ξ=(0.0054,0.3790,0.5983,0.0188,0)ξ3=0.5983较好#6ξ=(0,0.5313,0.4702,,0,0)ξ2=0.5313一般

由表9可知，各杆塔各防雷措施的实际权重值不同时，得到的最大隶属度不同，其评价等级也不同.评价等级最高的是#2杆塔，评价等级为好；接下来是#5杆塔，评价等级为较好；评价等级最低的是#1、#3、#4和#6杆塔，评价等级为一般.

5结论

(1)文中运用层次分析法构建了一个配网防雷评估模型，将复杂的防雷评估系统条理化、层次化，便于计算分析.采用10/10-18/2标度法计算各措施的权重值有利于减小人为主观因素的影响，使结果更符合客观实际，精确度更高.

(2)采用模糊综合评价法进行配网防雷措施等级评估能够快速、有效地对各线路进行评估，评估结果符合线路实际运行情况，具有较强的可信度.

(3)实际线路计算表明，采用同种措施的杆塔由于运行状况的不同，其评价等级不一定相同，要视具体权重值而定.文中安装了相同防雷措施的杆塔的评价等级有较大差异，评价等级最高的是#2杆塔，其次是#5杆塔，最后是#1、#3、#4和#6杆塔.

#1、#3、#4和#6杆塔虽然评价等级同样为一般，但是其隶属度值不同，它们间的评价等级高低不能单一地根据最大隶属度值的大小进行排序，其具体排序方法有待研究.

参考文献：

[1]ERIKSSON A J.An improved electro geometric model for transmission line shielding analysis [J].IEEE Transactions on Power Delivery,1987,2(3):859- 870.

[2]RIZK F A M.A model for switching impulse leader inception and breakdown of long air gaps [J].IEEE Transactions on Power Delivery,1989，4(1)：596- 606.

[3]THOMAS L Saaty.There is no mathematical validity for using fuzzy number crunching in the analytic hierarchy process [J].Journal of Systems Science and Systems Engineering，2006，15(4)：457- 464.

[4]张志劲，孙才新，蒋兴良，等.层次分析法在输电线路综合防雷措施评估中的应用 [J].电网技术，2005，29(14)：68- 72.

ZHANG Zhi-jin，SUN Cai-xin,JIANG Xing-liang，et al.Application of analytic hierarchy process in estimation of compositive transmission line lightning protection mea-sures [J].Power System Technology，2005，29(14)：68- 72.

[5]赵淳，阮江军，李晓岚，等.输电线路综合防雷措施技术经济性评估 [J].高电压技术，2011，37(2):290- 297.

ZHAO Chun，RUAN Jiang-jun，LI Xiao-lan，et al.Technology and economy evaluation of comprehensive transmission line lightning protection measures [J].High Voltage Engineering，2011，37(2):290- 297.

[6]姚敏，张森.模糊一致性矩阵及其在软科学中的应用 [J].系统工程，1997，15(2)：54- 56.

YAO Min，ZHANG Sen.Fuzzy consistent matrix and its applications in soft science [J].System Engineering，1997，15(2)：54- 56.

[7]舒康，梁镇韩.AHP中的指数标度法 [J].系统工程理论与实践，1990，10(1)：6- 8.

SHU Kang，LIANG Zhen-han.Index scale method of the AHP [J].System Engineering-Theory & Practice，1990，10(1)：6- 8.

[8]汪浩，马达.层次分析标度评价与新标度方法 [J].系统工程理论与实践，1993，13(5):24- 26.

WANG Hao，MA Da.Scale evaluation and new scale methods [J].System Engineering-Theory & Practice，1993，13(5)：24- 26.

[9]李蓓.模糊AHP在管理信息系统中的应用研究 [D].北京：中国地质大学地球科学与资源学院，2014.

[10]杜栋.论AHP的标度评价 [J].运筹与管理，2000，9(4):42- 45.

DU Dong.Evaluation on the scale of AHP [J].Operations Research and Management science，2000，9(4):42- 45.

[11]候岳衡，沈德家.指数标度及其与几种标度的比较 [J].系统工程理论与实践，1995，15(10)：43- 46.

HOU Yue-heng，SHEN De-jia.Index number scale and comparison with other scales [J].System Engineering-Theory & Practice，1995，15(10)：43- 46.

[12]刘颖芬，占济舟.比例标度一致性比较的新方法 [J].统计与决策，2007(8)：17- 18.

LIU Ying-fen，ZHAN Ji-zhou.A new method of comparison to proportion of scaling consistency [J].Statistics and Decision，2007(8)：17- 18.

[13]段若晨，王丰华，顾承昱，等.采用改进层次分析法综合评估500kV输电线路防雷改造效果 [J].高电压技术，2014，40(1)：131- 137.

DUANG Ruo-chen，WANG Feng-hua，GU Chen-yu，et al.Comprehensive evaluation of 500 kV transmission line lightning protection effect based on improved analytic hie-rarchy process [J].High Voltage Engineering，2014，40(1)：131- 137.

[14]李佩，杨伟.改进层次分析法和模糊灰尘色理论的管道土壤腐蚀评价 [J].油气储运，2006，25(4)：27- 33.

LI Pei，YANG Wei.Evaluation on the corrosion rate of pipeline with analytic hierarchy process and fuzzy comprehensive evaluation method [J].Oil & Gas Storage and Transportation，2006，25(4)：27- 33.

Application of Improved Analytic Hierarchy Process on Evaluation of Lightning Protection in Distribution Networks

LIUGang1MAHao-yu1ZHANGXian2

(1.School of Electric Power,South China University of Technology,Guangzhou 510640,Guangdong,China;2.Maintenance Branch Company,State Grid Hunan Electric Power Company, Changsha 41000, Hunan,China)

Abstract:In order to effectivelyreduce thelightning incidents of power transmission lines and ensure the safety of power systems, some measures should be adopted to improve the lightning withstand level of transmission lines. In this paper, based on an improved analytic hierarchy process(AHP) with new scale and the fuzzy comprehensive evaluation method(FCEM), a model suitable for evaluating the lightning protection measures of actual lines in power distribution networks is proposed, which comprehensively considerssuch factors as the reduction of trip-out rate, the impact of engineering cost, the effect of the target, the ease of maintenance andthe service life. Then, in accordance with the AHP, all the evaluation weights of lightning protection measures relative to the destination level are obtained, the memberships of the measures are determined via the FECM, and the optimal rehabilitation scheme is thus presented.The results show that the proposed evaluation system helps to effectively assess the power distribution lines and determine the optimal lightning protection measures as well as line rehabilitation scheme.

Key words:lightning protection; improved analytic hierarchy process; fuzzy comprehensive evaluation; new scale; effect evaluation

收稿日期:2015- 04- 13

*基金项目:广东省科技计划项目(2013B010405002)

Foundation item:Supported by Science and Technology Planning Project of Guangdong Province(2013B010405002)

作者简介:刘刚(1969-)，男，博士，副教授，主要从事智能高压电网、过电压及其防护、电力设备外绝缘研究.E-mail:liugang@scut.edu.cn

文章编号:1000- 565X(2016)04- 0071- 06

中图分类号：TM 726.3

doi：10.3969/j.issn.1000-565X.2016.04.011