基于磁流变效应的变参数切削颤振抑制方法研究*
谷 涛,张永亮,洪 明
(上海理工大学 机械工程学院,上海 200093)
基于磁流变效应的变参数切削颤振抑制方法研究*
谷涛,张永亮,洪明
(上海理工大学 机械工程学院,上海200093)
摘要:随着我国加工制造业的发展,提高切削加工水平成为发展制造业亟待解决的重要问题,而机床切削颤振一直是制约机械加工质量的最重要的因素之一。针对车削产生的颤振问题,设计了磁流变车削减振装置,并对其结构及减振机理进行了分析,建立起了磁流变车削装置的动力学模型。对不同波形、峰值及频率电流作用下的切削系统振动响应进行了理论分析及仿真,结果表明:幅值为6A、频率为1Hz的方波电流为此切削系统下的最佳控制电流;此外通过改变实验中电流变化峰值、频率及波形,将各个参数对减振效果的影响规律进行了研究与探讨。
关键词:磁流变;动力学模型;车削试验;MATLAB仿真
0引言
切削颤振是机床闭环切削系统的动态不稳定现象,它发生在切削刀具与工件之间,对产品质量、刀具及机床设备等的危害已毋庸质疑。目前,不少国内外学者对切削颤振控制方法进行研究,结果表明:各类切削颤振控制方法的本质就是在线调整机床切削系统的动态特性,以破坏切削颤振产生和发展的条件[1-4]。
近年来发展起来的半主动控制技术并借助智能材料优良的机-电耦合特性,兼具了主动控制适应性强和被动控制可靠性高的优点,且能耗较低[5-8],已逐步应用到切削颤振中。通过对磁流变液的流变特性的研究[9],设计了一种基于剪切模式的减振装置,通过理论建模、仿真分析及切削试验研究施加在减振装置上的电流参数——波形、幅值及频率的变化对车削系统动特性的影响规律,以探究抑制颤振的最佳电流参数,为有效利用磁流变效应控制切削颤振,提高加工精度提供理论基础和实践经验。
1车床横刀架磁流变减振装置结构及工作原理
外圆车削加工过程中,颤振的主振方向为图1中所示的y方向——即加工表面的法线方向。本文研制的剪切模式磁流变减振装置安装在车床横刀架的侧面,其安装示意图如图1所示。

图1 磁流变减振装置安装示意图
该减振装置的装配图如图2所示。该装置主要由上箱体组件和下箱体组成。上箱体组件主要包括上限位槽4、连接板5、上隔板6和上磁极7等零件,其中上隔板6和2个上极板7通过螺钉固定在上限位槽4上,上限位槽4则通过定位销和螺钉与连接板5定位并连接在一起,连接板5用螺钉固定在车床横刀架侧面,如图1所示,装置中的上箱体组件可以随横刀架做y向的移动。下体组件由两个下磁极2、一个下磁极8、固定板1和下箱体3组成。两个下磁极2通过下箱体3的侧面定位并用螺钉固定在其上,下磁极8通过下限位槽定位固定在下箱体3中。

1.下固定板 2.两侧下磁极 3.下箱体 4.上限位槽 5.连接板 6.上隔板7.上磁极 8.中间下磁极
图2床横刀架磁流变减振装置装配图
切削颤振过程在线圈上施加电流后,上、下磁极间产生磁场产生磁流变效应,磁流变液产生对应的的抗剪切屈服应力,上磁极振动所受的阻力也会增大,从而抑制刀架的振动,达到减振目的。
2基于磁流变装置的车床刀架动力学模型
磁流变减振装置的车床横刀架系统可由图2所示单自由度系统动力学模型来表示。a0(t)为名义切削厚度;y(t)为本次切削时的振动位移;y(t-T)为上次切削振动位移;M为系统总质量;F(t)为切削力;C0、K0阻尼系数和刚度系数;FI为磁流变减振装置产生的总阻尼力;β为切削力与主振方向的夹角。

图3 基于磁流变效应的车床横刀架系统动力学模型
对图3进行受力分析,可得系统的运动微分方程为:
(1)
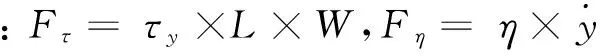
(2)
式中,H为减振装置上施加的磁场强度, L、W和k是与装置有关的结构参数,η是磁流变液未加磁场时的粘度,g是磁极间隙,所以本文磁流变减振装置产生的阻尼力表达式为:
(3)
式中,I为施加在减振装置上的励磁电流,将式(3)带入式(1),同时,令C=C0+8.53×η、F(t)=F0cosΩ0t,其中F0为切削力的最大幅值、Ω0为切削力的振动角频率,整理后可得:
F0cosΩ0tcosβ-20.6×I×k
(4)
式(4)表明系统振动响应是切削力和磁流变效应引起的库仑阻尼力两部分综合作用的结果。切削力引起的是简谐激励下的振动响应;磁流变效应引起的库仑阻尼力与电流的大小有关,因此将对不同电流波形、振幅及频率参数下进行理论仿真及试验研究。
3基于磁流变装置的变电流车削系统振动响
应仿真
对方波、半波正弦及三角波形3种电流波形下系统的振动响应进行分析,以方波电流为例进行理论推导,求得系统振动响应的表达式。方波电流可由公式(5)表示:
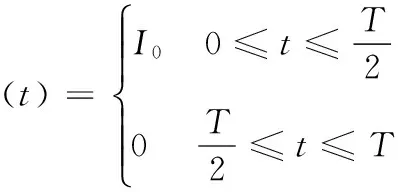
(5)
式中,I0为电流的振幅,T为电流的周期。由于方波波形属于周期函数,因此可以利用傅里叶级数将其展开为无限个简谐分量的叠加[10],可求得振动系统的稳态响应为:
(6)
3.1不同电流波形下车削系统振动响应仿真
利用Matlab进行仿真,仿真参数分别取为:C=4.605×104Ns/m,K0=1.8×107N/m,η=1.2,F0=200N,β=30°,k=1.42,M=20kg,角频率Ω=2π×1(即频率为1Hz),振幅I0=6A,得到方波、半波正弦和三角波电流的仿真结果分别如图4所示。
由上图可以发现,在三种不同的波形下,方波的理论仿真效果最明显;后文将以方波为基础,改变其参数进行仿真。
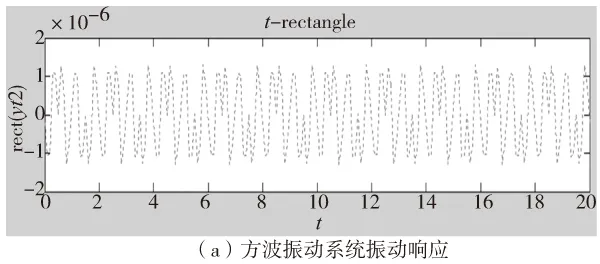


图4 不同电流波形下的振动仿真
3.2不同电流峰值下车削系统振动响应仿真
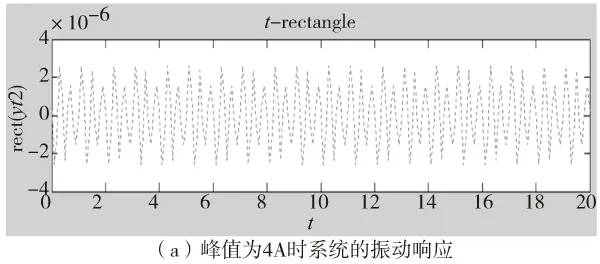


图5 不同电流值下的振动响应仿真
3.3不同电流频率下车削系统振动响应仿真

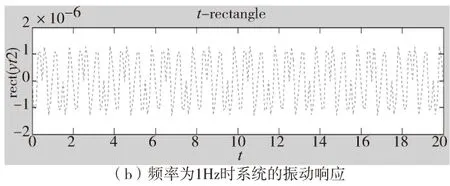

图6 不同电流频率下的振动响应仿真
由图5、图6果可知,方波在1Hz时减振效果最好,电流频率为1Hz时比0.5Hz和2Hz时振动幅值的波动要小。由此得出结论:频率过快与过慢都不利于减振。
因此方波是具有较好减振效果的波形。具有最佳抑振效果的电流峰值为6A,频率为1Hz,波形为方波。
4车削减振试验研究
在验证减振试验中,利用labview编写了加速度信号的采集及分析程序、方波电流信号的采集与控制程序,可直接读出方波峰值、频率下的切削响应信号。按图7所示磁流变减振系统框图连接好各仪器装置,切削材料为45#钢棒料,切削参数为:主轴转速400r/min,进给量0.08mm/r,切削深度0.6mm。

图7 车削减振试验系统
当电流频率为1Hz,幅度为6A,波形为方波电流信号下加电前后振动系统的时域和频域特征变化;
为了便于比较,如下两表列出其他几种不同参数下各种波形电流加电前后功率谱密度峰值比值表。

表1 不同波形及峰值下加电前后功率谱密度值对比表

表2 不同波形及频率下加电前后功率谱峰值对比表
表1为三角波与方波不同峰值下加电前后功率谱密度峰值比值表,表2为三角波与方波不同频率下加电前后功率谱密度峰值比值表。试验表明,方波比三角波,半正弦波减振效果都要好。电流过大过小的电流都不利于减振,这是由于磁流变液不是随着电流增加而一直增加,而是到达一定程度会出现磁饱和;所以峰值为6A电流减振效果最好;电流频率过大过小会导致磁流变切削系统固有频率的变化,过大的或过小的频率都不利于减振,所以最佳电流变化频率为1Hz。


图8 波电流幅值6A加电前后功率谱密度图
5结论
(1)建立了基于磁流变减振装置的车床横刀架系统动力学模型,分析了不同波形电流施加于磁流变减振装置上的切削系统的振动响应,并用Matlab对不同电流峰值、频率和波形下基于磁流变减振装置的切削系统振动响应进行了模拟仿真,理论分析表明:峰值为6A、频率为1Hz的方波电流为最佳控制电流。
(2)在CA6140车床上搭建了外圆车削减振试验。
分别改变施加于磁流变减振器上的电流变化幅值、频率及波形进行了车削减振试验,得到各个参数下功率谱图。结果表明:在此试验系统下,峰值为6A、频率为1Hz的方波电流具有最佳减振效果。
[参考文献]
[1] 吴雅.机床切削系统的颤振及其控制[M].北京:科学出版社,1993.
[2] Seguy S, Insperger T, Arnaud L, et al. On the Stability of High-Speed Milling With Spindle Speed Variation[J].Int. J. Adv. Manuf. Technol.,2010,48:883-895.
[3] M Zatarain, I Bediaga, J Munoa,et al.Stability of milling processes with continuous spindle speed variation: analysis in the frequency and time domains, and experimental correlation[J].CIRP Annals—Manufacturing Technology 2008,57(1):379-384.
[4] Hongrui Cao, Bing Li, Zhengjia He. Chatter stability of milling with speed-varying dynamics of spindles, Int. J. of MTM, 2012, 52(1):50-58.
[5] N H Kim, D Won, J C Ziegert. Numerical analysis and parameter study of a mechanical damper for use in long slender endmills,Int. J. of MTM,2006,46(5):500-507.
[6] Peter P Radecki, Kevin M Farinholt, Gyuhae Park, et al. Vibration Suppression in Cutting Tools Using a Collocated Piezoelectric Sensor/Actuator with an Adaptive Control Algorithm[J].Trans. of ASME, J. of Vibration and Acoustics,2010,132:477-487.
[7] M Wang, R Y Fei.On-line chatter detection and control in boring based on an electrorheological fluid[J].Mechatronics,2001,11:779-792.
[8]D Sathianarayanan,L Karunamoorthy,J Srinivasan, et al.Chatter suppression in boring operation using magnetorheological fluid damper[J].Material Manufacturing Process,2008,23:329-335.
[9] 周 云,谭 平. 磁流变阻尼控制理论与技术[M]. 北京:科学出版社,2007.
[10] 孔繁森, 赵新刚, 刘春颖.切削过程混沌颤振的控制方法仿真研究[J].振动与冲击, 2008, 27(11):22-27.
(编辑赵蓉)
Cutting Chatter Suppression Method Research Based on the Variable Parameters of the Magnetorheological Effect
GU Tao,ZHANG Yong-liang,HONG Ming
(School of Mechanical Engineering,University of Shanghai for Science and Technology,Shanghai 200093,China)
Abstract:With the development of manufacturing industry in our country, improving the level of machining has become an important problem urgently to be solved in development of manufacturing industry, while the machine tool cutting chatter is an important factor of influence to cutting quality. To suppress chatter on cutting system, a device for turning chatter suppression based on magneto-rheological (MRF) is developed. The dynamical model of MRF turning device was established through analyzing its working principle and structure. The vibration responses were analyzed theoretically and simulated by MATLAB under different waveforms, peak and frequency of current. The conclusions were drawn that the optimum control current is square wave with amplitude equal to 6A and frequency equal to 1Hz in the turning system of this paper. In addition, the chatter suppressive experiments were conducted under different waveforms, peak and frequency of current, the influence law of above current parameters on chatter suppressive effect was researched and discussed.
Key words:magneto-rheological fluid; dynamical model; cutting experiments; MATLAB simulation
文章编号:1001-2265(2016)06-0067-04
DOI:10.13462/j.cnki.mmtamt.2016.06.017
收稿日期:2015-01-26;修回日期:2015-03-05
*基金项目:国家自然科学基金(51205255)
作者简介:谷涛(1989—),男,河南信阳人,上海理工大学硕士研究生,研究方向为机械减振,(E-mail)giter6168@163.com。
中图分类号:TH166;TG659
文献标识码:A

