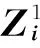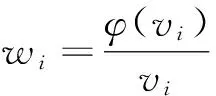PCB基准点的探针式鲁棒定位方法*

曾　友，高　健，岑　誉

(广东工业大学 机电工程学院 机械装备制造与控制技术教育部重点实验室,广州　510006)

PCB基准点的探针式鲁棒定位方法*

曾友，高健，岑誉

(广东工业大学 机电工程学院 机械装备制造与控制技术教育部重点实验室,广州510006)

摘要：为了提高印刷电路板(PCB)基准点的定位鲁棒性与定位精度，减少因基准点损坏而定位不准或者不能定位现象，提出了探针式基准点定位方法。该方法分粗定位与精定位两步，粗定位阶段首先采用区域增长法进行图像分割，通过圆度阈值筛选出圆形区域，运用所提出的探针定位方法建立探针法数学模型，实现基准点的粗定位。基于粗定位所得基准点区域图像，提取其图像亚像素边缘，提出基于稳健估计算法的几何距离法圆拟合方法，实现基准点的精定位。实验结果表明：在复杂背景下该探针式定位法的基准点识别结果的正确率达100%，可有效降低基准点误定率；定位方法对基准点污损不敏感，在基准点损坏50%的情况下定位精度还能达到0.021个像素。

关键词：PCB基准点；计算机视觉定位；探针法；边缘检测；几何法圆拟合

0引言

基准点是PCB板上的定位标识，常见形状有圆形、菱形、三角形和十字形等，其中以圆形居多[1]。在表面贴装技术中，PCB板上各元件位置都以基准点为基准，因此怎样快速准确的找到基准点位置成为表贴装工艺中一个极其关键环节。这一任务由贴片机机器视觉系统实现。定位的精确度、稳定性以及定位速度等是衡量视觉定位系统好坏的性能指标。对于圆形基准点，传统定位方式主要有：Hough变换、曲线拟合、边缘检测以及模板匹配等[2]。这些方法各有其特点，如Hough变换，虽然定位精度高，但耗时长[3-4]，限制了该方法的工程实际应用。为了提高定位系统的性能，国内外许多研究者都投入了相当多的精力，如夏奇等应用不变矩判断基准点的存在并用点模式匹配计算基准点的位置偏差[5]；柏长冰等人提出Hough变换快速检测圆形PCB 基准[6]；熊光游等人提出基于最圆椭圆度的基准点中心位置定位算法[2]，Fang Lei等人提出广义快速Hough变换定位方法[7]。

现有新颖的基准点定位方法无论从定位精度还是定位速度都较传统方法有很大程度提高，但还存在不足。模板匹配法对基准点质量要求较高，如果基准点出现污损，则会出现检测不准甚至检测不到的现象。除模板匹配外，其它方法在阈值分割和圆的寻找部分存在两个问题：①难以找到一个合适的分割阈值把所有照片中所需要的目标分割出来，其操作对图片质量的要求非常高。虽然Ostu等自动阈值分割方法具有一定的优势，但对于复杂污损图片，其分割准确性也受影响。②没有考虑其它干扰因素。如果一张图片中存在两个甚至更多的圆形物或者所得圆形点非基准点，这些方法难以辨别出真正的基准点。为了解决上述两个问题的困扰，本文提出了一种新的鲁棒性较高的基准点识别定位方法，可实现复杂背景图片下基准点的准确精密定位。

1探针法提取基准点

基准点图片经区域分割后，必须通过有效方法确定基准点所在区域。传统方法是根据基准点圆度和区域面积来获得，这种方法大多数情况下能准确提取出基准点，但在如下情况存在缺陷：①存在与基准点圆度和面积差不多的干扰区域；②当摄像机拍照的角度或者高度变化时，基准点在照片里的面积会改变。 本文根据基准点特征，提出了一种新的获得基准点方法。

1.1圆形基准点特征

基准点组成如图1所示，它具有如下特征：

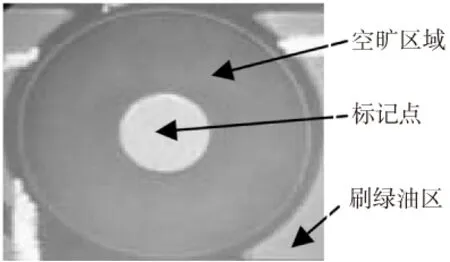
图1　基准点组成

(1)它是一种圆形标志；

(2)一个完整的基准点包括标记点和空旷区域，且r≥2R(r为空旷区域半径，R为基准点半径，通常r=3R)。标记点常为裸铜等反光度高的材质，PCB板空旷区域反光度低，在灰度图片中表现为暗色，空旷区域以外为刷绿油区，根据光源颜色不同，反光度不同。视觉定位所采集到的基准点图片，标记点、空旷区与刷绿油区的灰度表现层次分明。本文采用自然光照射，用一过基准点圆心直线扫描基准点，灰度变化曲线如图2。由此图可知，基准点区域灰度值高达255，空旷区域灰度值低至90，刷绿油区灰度值又高达230。

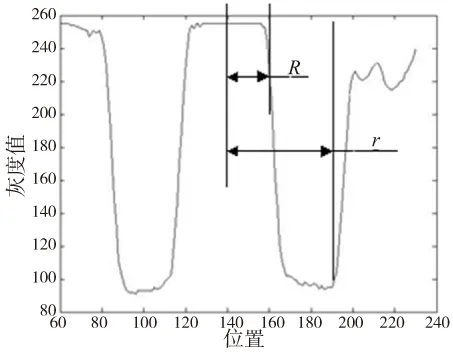
图2　灰度变化曲线

1.2探针法实施步骤

由于圆形基准点存在如上特征，提出如下方法：

(1)根据圆形特征，选择区域增长法分割后圆度为0.9以上的区域，去掉圆度0.9以下的区域。圆度定义公式如下：

(1)

(2)

(3)

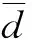
(2)由于是粗定位，考虑到定位时间问题，选用计算量少的形心法对步骤(1)获得的圆形区域求中心，公式如下：

(4)

其中，(x0,y0)表示基准点粗定位中心，R表示圆形区域半径，i,j分别表示圆形区域在行和列方向像素坐标，N表示整个圆形区域像素总数，S表示圆形区域。

以此中心为起点，在水平和垂直方向线扫描原图，当扫描图形像素值变化趋势与图2近似则判定为基准点。为节省程序运行时间，本文用探针的方式只对部分像素点进行比较。具体方法如下：

选取一方向，如水平或竖直方向，也可多方向，在中心点到R范围内，从中心点开始以一定规律提取像素点灰度值，比如隔点取值，共取N个像素值，最后将N个样品的像素值求均值Gm1。依此方法，分别从1.5R和3.5R处开始，以相同的规律，和分别为Gm2与Gm3。此规律数学模型如下：

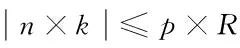
(5)

其中，G(i,j)表示图片第i，j点灰度值，(cx,cy)为粗定位所得中心,ni，nj,ki,kj取整数，ki,kj值用来控制采样间隔，p为权值，控制采样范围，范围小则耗时短，为保证检测效果推荐值为0.8。

公式(5)就如用一个探针取指定位置的值，因此命名为探针法。在本文光源条件下，如果Gm2

2基准点精确定位

经粗定位后，为获得基准点精确位置，先提取图像像素边缘，再进行亚像素边缘提取，最后进行圆拟合得到圆心，实现精确定位。

2.1亚像素边缘提取

图像边缘是表现为像素值的变化，边缘处像素值变化如图3a所示，亚像素边缘提取需先得到目标像素边缘，像素边缘的提采用经典的Canny算子[8]，它具有高定位精度，低误判率，能抑制虚假边缘，对噪声不敏感等特点。参数拟合法是根据边缘点及其邻域内的点的灰度变化呈高斯分布的原理来获取亚像素边缘点的一种方法[9]。经Canny算子获得像素边缘后可得到每个像素的边缘点方向，以边缘点为中心，沿边缘方向拓展3个像素，将得到 7个像素点的像素值，在此边缘点方向像素值的差分呈现高斯分布，如图3b所示，因此拟合此高斯曲线，获得最高点的坐标值即为图像边缘的亚像素坐标。

图3　两种图像边缘灰度变化表示方法

2.2基于稳健估计的几何距离法圆拟合

有两种方法进行圆拟合，一种是代数法，另一种是几何法。代数法是计算2.1节所得边缘点集到某圆圆心的距离与此圆半径之差的总和，当此总和最小时所得的圆即为最终所得圆。代数拟合法具有易程序实施与运算时间短等优点，但它却具有精度不高，有悖测量准则及所得参数不可靠等缺点，几何法被认为可能是唯一能解决代数法上述缺点的方法[10]，因此本文用几何法进行拟合。

图4　几何法拟合圆示原理图

几何法计算的是边缘点集到几何特征正交距离也即最短距离，如图4所示，点A到点B的距离是几何法所关心的。对于半径为R，圆心为C(XC,YC)可用下式表示，其中Z为边缘点A指向点B向量，ZC表示点A指向圆心的向量：

(6)

(7)

正交距离向量如下：

(8)

这是一个已知图像边缘点集坐标(Xi,Yi)求圆心C(XC,YC)和半径R的非线性方程，需用迭代法求解。由于2.1节所得亚像素边缘中存在误差很大的点，如图5最左边的亚像素边缘点，这些点将对式(8)拟合所得结果造成影响，因此必需减小或者去除这些误差大的点的影响，这里采用M估计中的选权迭代法求解式(8)，其中权值用稳健估计中的Tukey法获得。

图5　像素边缘和亚像素边缘

(9)

以ρ(·)代替-lnf(·),则有：

(10)

(11)

M估计就是式(9)定义的一类估计，一个ρ函数定义一个M估计，选取正确的ρ函数是M估计的关键。

设观测值为L(为n维向量)，未知参数向量X，针对圆拟合，L为所得边缘点集的Xi，Yi坐标值组成的向量，X则为圆心C(XC,YC)与半径R组成的向量(XC,YC,R)。误差方程及观测权阵如下：

(12)

因此，可将M估计的ρ函数必写为：

(13)

由公式(11)、(12)、(13)可得：

BTWV=0

(14)

将式(12)代入式(16)并加入权阵P，可得：

(15)

针对本文的圆拟合，结合公式(8)、(12)得单点误差方程：

(16)

其中，V=(AB+R)2,所有亚像素边缘点用式(16)表达，将其转化为矩阵形式则形如公式(8),其中：

(17)

(18)

3实验结果分析

实验所使用的计算机为64位操作系统，处理器3.30GHz，4GB内存，软件环境为VS2010/C++配置openCV。

3.1算法鲁棒性

为检测算法的鲁棒性，拍摄了一组基准点图片，共50张，照片中背景复杂，大量的圆形区域会对基准点的检测产生干扰，且图片质量有好有坏，图6中例举出了其中三张，十字架表示为检测到的基准点中心。

(a)采用本文所述探针法

(b)传统方法

50张图片中采用本文所述探针法正确检测率为100%，如图6a，而采用无探针方法则在这种复杂背景下由于圆形区域的干扰发生误检或者不能检测，准确率仅为10%，大部分产生误定位，如图6b所示，其中第一张定位正确，第二张图因背景过于复杂定位不准,第三张图存在与基准点面积相似的圆形点而定位错误。由此证明所述探针法能提高正确检测率，具有很高的鲁棒性。

3.2准确性比较

为检验准确性，将本文方法与灰度重心法、标准最小二乘法、几何法及基于稳健估计的代数法共四种方法进行了比较。实验条件有限，无法直接测量实际PCB板基准点座标，因此实验分定性比较与定量两步比较，定性比较采用实际基准点照片，定量比较采用仿真方式，下面分别叙述。

3.2.1定性比较

图7　定性比较

定性比较是利用实际PCB板基准点图片分别用上述方法分别拟合，观察出各拟合效果。为使得各拟合效果出现明显区别，实际基准点被毁坏，毁坏程度分别为0，1/4与1/2，结果见图7。

图7中的交叉代表圆心，为使结果易于观察，将图片放大。图7a、7b、拟合效果差别不大；图7c、7d中只有基于Tukey估计的代数法与本文方法都取得了理想的效果；图7e、7f中明显可以看出只有本文效果最佳。

3.2.2定量比较

定量比较采用仿真法，利用图像处理软件PS生成组分辨率为320×128的基准点图片，见图8，图8a为理想圆形基准点，图8b、8c、8d为在图8a的基础上对圆进行了不同程度的损坏。圆形基准点像素级圆心为(160，128)，这里指的是第(160，128)个成像单元，如果进行亚像素拟合求圆心，理论圆心位置为(159.5，127.5)，半径为60个像素。拟合结果见表1。

(a)理想基准点　　　　　　　(b)边缘有偏差基准点

(c)1/4损坏基准点　　　　　　　(d)1/2损坏基准

实验灰度重心法行列误差位置误差最小二乘拟合法行列误差位置误差几何法行列误差位置误差a(0,0)0(0,0)0(0,0)0b(0.41,1.25)1.32(0.48,1.18)1.28(0.40,1.10)1.17c(7.17,7.43)10.33(4.98,5.20)7.20(7.40,7.75)10.72d(0,26.54)26.54(0,20.86)20.86(0.02,26.12)26.12实验Tukey稳健估计的代数法行列误差位置误差本文所述方法行列误差位置误差a(0.003,0.005)0.002(0,0)0b(0.82,1.40)1.62(0.005,0.029)0.029c(1.34,1.40)1.94(0.005,0.006)0.008d(0,18.10)18.10(0,0.021)0.021

由表1可以看出，在损坏程度由大到小(图8a～8d)其它方法误差逐渐增加，当损坏程度达到图8d所示将近1/2时，其它几种方法误差达到18个像素以上而本文所述方法还能保持0.021个像素，说明本文所述方法在精度上远远优于其它方法，且稳定性高。在运行时间上与其它几种方法相差不大，能控制在4ms以下，远远达到实际需求。

4总结

随着电子元件的小微化发展，PCB板定位的鲁棒性与精度要求越来越高，文中提出了一种PCB基准点探针式鲁棒识别定位方法，有效解决了复杂背景图像中基准点的误定位问题，增加了定位的鲁棒性。结合基于稳健估计的几何法圆拟合方法，达到了高精度定位效果。所提出的定位方法具有对基准点污损不敏感的特点，实验结果表明，即使污损部分占据到整个基准点图片的1/2，也还能获得良好的定位效果，定位精度高达0.021个像素。

[参考文献]

[1] 陈臣.印制电路板的自动光学检测系统的设计与研究[D].南京：南京航空航天学, 2010.

[2] 熊光洁,马树元,刘瑞祯.PCB检测中圆Mark的快速精确定位[J].计算机工程,2012,38(11):211-216.

[3] Yuan-xin ZHU，Bridget CARRAGHER，Fabrice MOUCHE，et al. Automatic Particle Detection Through Efficient Hough Transforms[J]. IEEE Transactions on Medical Imaging，2003，22(9)：1053-1062.

[4] Pekka KULTANEN，Lei XU，Erkki OJA. Randomized Hough Transform (RHT)[C]. Proceedings of the 10th International Conference on Pattern Recognition ,New Jersey：IEEE，1990:631-635.

[5] 夏奇，周明采，汪宏晟,等.高精度自动贴片视觉对准系统及其图像处理[J].光学技术，2004，30(2):146-149.

[6] 柏长冰，齐春，宋福民,等.Hough变换快速检测圆形PCB Mark[J].光电工程，2005，32(9)：75-78.

[7] Fang Lei,Jun Cheng,Siyu Guo,et al.A locating algorithm based on OGHT for PCB mark orientation[C].2010 International Conference on Information,Networking and Automation(ICINA 2010),Kunming,China: IEEE,2010:396-400.

[8] 邓仕超,刘铁根,萧泽新.应用Canny算法和灰度等高线的金相组织封闭边缘提取[J].光学精密工程, 2010,18(10):2314-2323.

[9] 张虎.亚像素技术与摄像机标定技术的研究[D].南京:东南大学,2010.

[10] S J Ahn, W Rauh,H J Warnecke. Least-squares orthogonal distances fitting of circle,sphere, ellipse, hyperbola, and parabola[J]. Pattern Recognition,2001, 34: 2283-2303.

[11] HANAN E,ROLAND F.ROBUST FITTING OF INARCH MODELS[J].Journal of Time Series Analysis,2014, 35: 517-535.

(编辑赵蓉)

Robust Probe Type Positioning Method for the PCB Mark Point

ZENG You,GAO Jian,CEN Yu

(School of Electromechanical Engineering, Key Laboratory of Mechanical Equipment Manufacturing & Control Technology of Ministry of Education, Guangdong University of Technology, Guangzhou 510006, China)

Abstract：In order to improve the robustness of localization and positioning accuracy of PCB(Printed circuit board), reduce the phenomenon of wrong location or unable location for the damaged mark point,a probe method is proposed.The method is divided into the coarse positioning and the accurate positioning.About the coarse stage: First, using the region growing algorithm to segment the image.Then choose the circular region with roundness threshold.At last the probe detection method is proposed and a mathematical model is set up to complete the coarse positioning.At the accurate positioning stage,the sub-pixel edge of the image should be obtain first.Then using the geometry method and combining the robust estimation method,the circle of the mark point is fitted,so the accurate positioning is completed.The experimental results show that the probe method is effective,its right positioning rate is as high as 100% under the complicated background.This means that the wrong positioning rate is highly decreased.The results also shows that the circle fitting method is not sensitive with the damage and stains.The positioning accuracy can reach 0.021 pixel even though the mark point is damaged 50%.Its effect is far superior to the other method described in this paper.The requirements of mark point positioning of stable,reliable,high accuracy and low sensitivity of damage and stains are reached.

Key words：PCB mark point;computer vision positioning;probe method;edge detection;geometry fitting circle

文章编号：1001-2265(2016)06-0030-05

DOI:10.13462/j.cnki.mmtamt.2016.06.008

收稿日期：2015-05-27

*基金项目：国家重点基础研究发展计划项目(973计划)(2011CB013104)；广东省高等学校科技创新重点项目(2012CXZD0020)；广东省战略性新兴产业专项资金(2012A080303004，2011A081301001)

作者简介：曾友(1990—)，男，湖南邵阳人，广东工业大学硕士研究生，研究方向为图像处理，(E-mail)1123838773@qq.com；高健(1964—)，女，山东青岛人，广东工业大学教授，博士生导师，研究方向为在线检测和机器视觉技术。

中图分类号：TH16;TG506

文献标识码：A