基于三次多项式曲线的轨迹平滑压缩算法*

李　浩，黄　艳，马岩蔚

(1.中国科学院大学，北京　100049；2.中国科学院沈阳计算技术研究所 高档数控国家工程研究中心，沈阳 110168；3.沈阳高精数控技术有限公司，沈阳　110168)

基于三次多项式曲线的轨迹平滑压缩算法*

李浩1,2，黄艳2,3，马岩蔚3

(1.中国科学院大学，北京100049；2.中国科学院沈阳计算技术研究所 高档数控国家工程研究中心，沈阳 110168；3.沈阳高精数控技术有限公司，沈阳110168)

摘要：针对由复杂曲线或复杂分量所组成的数控加工轨迹，采用通用的插补算法难以保证其插补精度与插补速度。因此文章在分析了已有插补算法不足的基础上，提出了一种基于三次多项式曲线的轨迹平滑压缩算法，该算法通过判断相邻微小线段之间的转角大小和微小线段的段长，将待加工轨迹划分为连续微小线段加工区和非连续微小线段加工区，并将其转接处的指令点设置为特征指令点。对于连续微小线段加工区，在满足加工精度的条件下，对其进行曲线拟合将折线加工路径转化成平滑曲线加工路径，以达到压缩程序段数目和平滑加工轨迹的目的。实验结果表明，该算法可以有效地提高数控加工的效率和质量。

关键词：三次多项式；轨迹压缩；特征指令点

0引言

现在复杂零件的加工程序都是先由设计人员通过计算机辅助设计软件进行设计，再利用计算机辅助制造软件将其细分成“巨量的微线段”，如果单纯依赖直线插补或圆弧插补，将严重降低加工速度甚至产生速度波动，而速度不稳定会直接影响加工精度，针对该问题国内的学者提出了一系列的解决方法。

吕强等[1]提出在现有小线段基础上，通过对进给速度、加速度、加工误差等进行限制，来实现速度平滑，即在机床的运动过程中，以某一进给速度从微段的终点处，直接改变速度方向进入到下一微段。使用这种方式，可以使得通过相邻路径段间的速度不必减小到零，从而提高了平均加工速度，同时也降低了对数控机床的冲击，提高了加工精度。但这种方式只是停留在由CAM生成的大量微小线段的处理上，并没有从本质上实现高速高精加工，也没有减少程序量。皮佑国[2]、林峰等[3-7]提出通过插值或拟合的方式“再现”或反算出零件的几何曲线曲面，即使用CAM生成的大量微小线段的数据信息，利用多项式曲线，B样条,C样条或者NURBS曲线，来进行曲线或曲面的重构。这种方法在轮廓误差方面取得了较好的效果，但是要利用所有的微段数据信息进行拟合，数据处理量大，加工效率低下。

为了解决该问题，大量的学者[8-9]针对选取特征点、曲线压缩等方法进行研究，这些方法不仅可以有效地减少所需处理的数据量，还能保证加工的精度。因此基于该思想本文提出了基于三次多项式曲线的轨迹平滑压缩算法，该算法从待加工路径中寻找出连续微小线段加工区域，并在满足加工精度的要求下将其拟合成平滑的三次多项式加工曲线，从而达到提高数控加工效率和表面加工质量的目的。

1轨迹平滑压缩算法

基于三次多项式曲线的轨迹平滑压缩算法主要是从CAD/CAM生成的大量微小线段中识别出可重构的连续加工区域，在满足逼近精度误差的条件下，将由大量微小线段组成的折线加工轨迹转化为由少量三次多项式曲线组成的平滑加工轨迹，从而实现程序段数量的压缩和加工轨迹的平滑。

该算法由特征点选取和特征点拟合两部分组成，其中特征点的选取依赖于相邻微小线段间允许通过最大速度的转角条件和相邻微小线段间段长相关变化的段长条件；特征点拟合是将两个特征指令点之间的折线加工轨迹转化成平滑的曲线加工轨迹。

1.1转角条件

在加工过程中，刀具到达B点时的进给速度为VB，加速度为αB，然后刀具进入路径段BC，路径段AB与路径段BC之间的夹角为α，如图1所示。

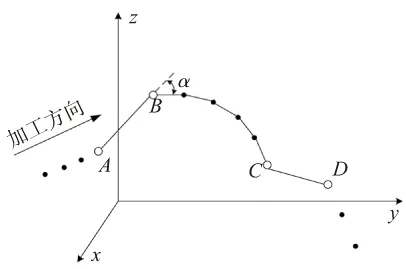
图1　加工路径段及其转角

设J为最大加加速度，A为最大加速度，T为插补周期，F为指令速度，由A和J可以计算出相邻路径段拐角处的最大进给速度和加速度[10]。

令VB=F，αB=A，得

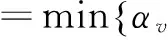
α=0～α基

(1)

公式(1)即是识别连续微小线段重构区的转角条件。当α>α基时，设置该两条直线微段的交点为特征点。

1.2段长条件

在特征点的选取中，还需要考虑微小线段的段长，来作为划分微小线段连续区域与非连续区域的条件。

使用圆弧逼近，根据相邻两微线段之间的转角α和当前微小线段的弓高误差δ，可以求出当前微段的弦长和圆弧半径，如图2所示。

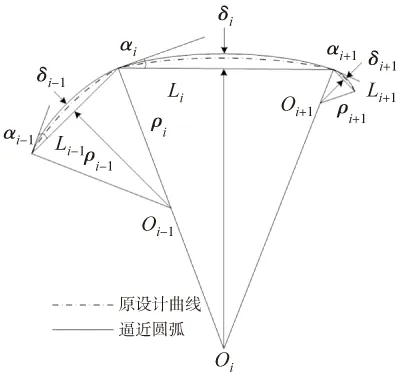
图2　相邻路径段夹角及段长关系

由于满足夹角条件，并且微段的段长比较短，所以可以使用圆弧半径来近似原曲线的平均曲率半径。

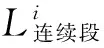
(2)

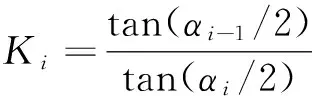
(3)

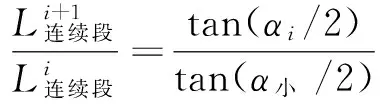
(4)

综合式(3)、(4)可得：

(5)

公式(5)即为识别连续微小线段重构区的段长条件。当不满足公式(5)时，将该微段的终点点设置为特征点。

如果不符合公式(1)或者公式(5)，则将该相邻微段的交点设置为特征点。如图1所示，点A、B、C、D即为不符合公式(1)或者公式(5)的特征点，而BC两个特征点之间所包含的微线段则可以拟合成平滑的加工曲线，因此BC为连续微小线段加工区，而剩下的微段AB和CD则是非连续区。

1.3特征点拟合

对于每个连续微小线段加工区域，采用分段的三次多项式曲线进行拟合，以达到平滑加工路径和压缩程序段数目的目的。

f(p)=a+bp+cp2+dp3(0≤p≤pl)

令每段四个数据点分别对应p=0，p=pl/3，p=2pl/3，p=pl时多项式的值，即可得到多项式的系数为：

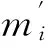
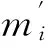
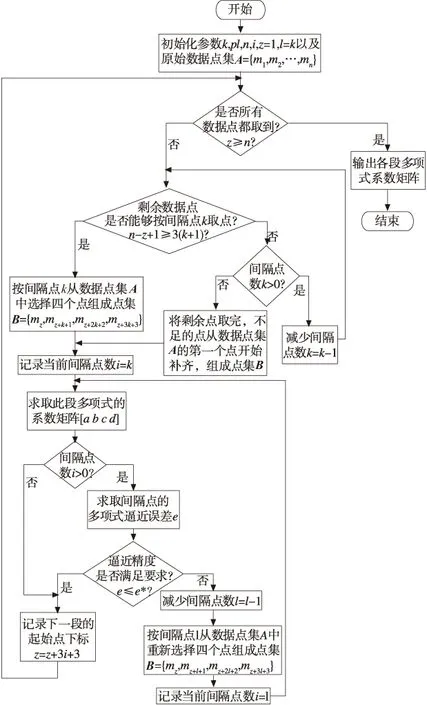
图3　多项式逼近精度控制流程图

若多项式逼近精度符合要求，则将多项式的最后一个数据点作为下一段多项式的数据起点，即将第一个数据点的下标设置为z=z+m*k+m，并在数据点集A中按照间隔点k选取下一段多项式逼近所需要的三个数据点，按照上述方法计算下一段多项式的系数。如果多项式的逼近精度大于e*，则缩小间隔点k的值，使k=k-l，从数据点集A中选取所需要的三个数据点，再按照以上述方法计算该段多项式的系数，重复该过程直到多项式的逼近精度小于e*。多项式逼近精度控制的流程图如图3所示。

2实验验证与分析

为了验证该平滑压缩算法的可行性和有效性，本文使用CAD/CAM软件UG，在插补周期T=2ms，进给速度V=300mm/s，最大加速度A=1000mm/s2,最大加加速度J=5000mm/s3，k=4，pl=0.09，e*=0.001mm的条件下，对图4所示的曲面进行加工仿真验证，并对比分析使用了该算法和未使用该算法的测试结果。

图4　待加工曲面

为分析该平滑压缩算法对工件加工表面产生的影响，本文对插补点所构成的加工路径进行分析。

未使用该算法的加工路径如图5a所示，而使用了该算法的加工路径如图5b所示。通过对两加工路径图进行对比，发现采用该算法后，加工路径明显变得平滑，比未采用该算法时消除了相邻路径段之间的夹角，这是由于该算法，是在基于特征点拟合生成的平滑样条曲线上进行的插值点计算，因此可以有效地减小插值点与原始模型之间的偏差。

(a)未采用平滑压缩算法

(b)采用平滑压缩算法

为了进一步分析加工速度的变化对加工效率的影响，本文只对由15条小线段组成的加工路径的速度进行分析，具体加工路径如图6。

图6　加工轨迹

未使用该算法的加工速度如图7a所示，而使用了该算法的加工速度如图7b所示。通过对两速度曲线图进行对比，发现采用该算法后，加工时间明显缩短，比未采用该算法时减少了0.782s，这是由于该算法平滑了加工路径，提高了转接点的速度，因此该算法确实可以提高零件的加工效率。

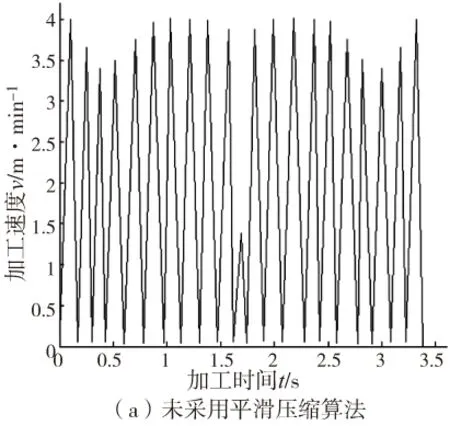
(a)未采用平滑压缩算法

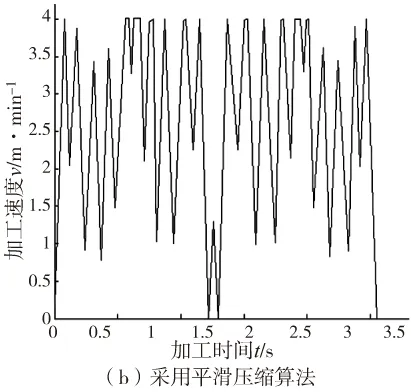
(b)采用平滑压缩算法

3结论

本文提出的基于三次多项式曲线的轨迹平滑压缩算法，能够根据“巨量微小线段”的转角和段长条件反映出曲线曲率的变化情况，有效地区分出加工路径中的可重构区域和非可重构区域，并对连续的可重构区域进行重构，重构之后的曲线能够在满足逼近精度误差的条件下缩短程序段数目，平滑加工路径，提高加工效率和零件表面的加工质量。

[参考文献]

[1] 吕强，张辉，杨开明,等. 基于实时性要求的多段预读速度规划方法及实验研究[J]. 机床与液压，2008，36(4)：1-4.

[2] 皮佑国，范德和. 数控加工中连续微线段轨迹的B样条曲线拟合[J]. 华南理工大学学报，2012，11(1)：53-57.

[3] WEN Wei-bin, JIAN Kai, LUO Shao-ming. 2D numerical manifold method based on quartic uniform B-spline interpolation and its application in thin plate bending[J]. Applied Mathematics and Mechanics,2013,34(8): 1017-1030.

[4] Yunsen Wang, Dongsheng Yang. A real-time look-ahead interpolation algorithm based on Akima curve fitting[J]. 2014, 85(10): 122-130.

[5] 林峰，汪池. 三次非均匀B样条曲线插补算法研究[J]. 组合机床与自动化加工技术，2012(8)：32-35.

[6] 尹池江，檀结庆. 带多形状参数的三角多项式均匀B样条曲线曲面[J]. 计算机辅助设计与图形学学报，2011，23(7)：1131-1138.

[7] 粟烂芝，王品. NURBS曲线自适应插值拟合算法[J]. 组合机床与自动化加工技术，2011(1)：186-191.

[8] 韩江，江本赤，夏链,等.基于轮廓关键点的B样条曲线拟合算法[J]. 应用数学和力学，2015，4(1)：424-431.

[9] 赵晟，毕庆贞，王宇晗,等. 基于G2连续Bézier曲线的刀具轨迹压缩算法[J]. 上海交通大学学报，2014，11(5)：629-635.

[10] 王海涛，赵东标，高素美. CNC自适应速度前瞻控制算法的研究[J]. 机械科学与技术，2009，14(3)：346-349.

(编辑赵蓉)

The Smooth Compression Algorithm Based on Cubic Polynomial Curve

LI Hao1,2，HUANG Yan2,3，MA Yan-wei3

(1. University of Chinese Academy of Sciences, Beijing 100049, China; 2. National Engineering Research Center for High-End CNC, Shenyang Institute of Computing Technology, Chinese Academy of Sciences, Shenyang 110168, China)

Abstract：For the NC machining paths which consists of complex curves or complex components, the general interpolation algorithm can not guarantee its accuracy and speed. So after analyzing the disadvantages of current interpolation algorithms, this paper proposed a smooth compression algorithm based on cubic polynomial curve. To begin with, based on the angles and lengths evaluated from the adjacent command points, continuous micro-line blocks are recognized from the machining paths of free-form, and feature points are selected. Then, for those blocks, they are fitted into a cubic polynomial curve to compress blocks and smooth contours. Lastly the experimental results show that the proposed algorithm can improve the efficiency and quality of the NC machining.

Key words：cubic polynomial; path compression; feature point

文章编号：1001-2265(2016)06-0012-04

DOI:10.13462/j.cnki.mmtamt.2016.06.004

收稿日期：2015-06-15；修回日期：2015-06-18

*基金项目：“高档数控机床与基础制造装备”国家科技重大专项：数控系统功能安全技术研究(2014ZX04009-031)

作者简介：李浩(1990—)，男，河南人，中国科学院大学硕士研究生，研究方向为计算机软件与理论，(E-mail)lihaomew@mail.ustc.edu.cn。

中图分类号：TH166;TG659

文献标识码：A