基于逆向建模的复杂焊缝数学模型的建立方法*
李 静,李 君,郝卫东
(1.桂林电子科技大学信息科技学院 机电工程系,广西 桂林 541004;2.桂林电子科技大学 机电工程学院,广西 桂林 541004)
基于逆向建模的复杂焊缝数学模型的建立方法*
李静1,李君2,郝卫东2
(1.桂林电子科技大学信息科技学院 机电工程系,广西 桂林 541004;2.桂林电子科技大学 机电工程学院,广西 桂林 541004)
摘要:目前在复杂焊缝的自动化焊接中焊缝数学模型建立方法均比较复杂,针对焊缝特征模型设计一种等分离散建模算法。采用辅助测量设备测量工件上设置的点,已知曲线上两点间坐标系的旋转矩阵,由Euler定理将旋转矩阵转换为指数映射形式,通过等分旋转角,建立曲线上两点间及其它离散点处的坐标系。在Matlab环境下,对管道插接焊缝进行了建模分析。仿真结果表明采用等分离散算法建立的焊缝特征模型能达到预期的效果,且方法简单、效率高。
关键词:复杂焊缝模型;逆向建模;离散算法;相贯线
0引言
在离线编程技术的应用过程中,需要建立焊缝特征模型,必须解决实际作业与离线编程环境中的模型对象的校正问题,即坐标系标定问题[1-2]。文献[3-4]中的机器人参数标定方法可以达到很高的标定精度,但是标定过程复杂,需要耗费大量的时间来完成这项工作。文献[5-7]中采用三维光学扫描技术逆向建立焊缝模型,复杂的焊接环境,增加了图像处理和建立三维模型的难度,还很难快速的建立高精度的焊缝模型。文中采用辅助测量设备测量焊缝特征点,建立焊缝模型的方法。操作者只需要操作测量设备对设置的工件特征点进行测量便可以建立焊缝特征模型。管道相贯线焊缝是较为典型的复杂焊缝,对其的研究也很多。文献[8-11]中建立了相贯线焊缝模型和焊枪姿态模型,采用的建模方法有两种,一是在离散点处直接建立姿态矩阵,采用该方法建立的特征模型精度高但计算量大;二是对起始点的姿态变换矩阵等分离散间接建立离散点处的姿态矩阵,这种方法能有效的降低计算量但建立的焊缝模型有一定的误差,且误差不易控制。文中采用旋量理论间接建立焊缝特征模型,可以在不增加计算量的前提下有效的控制建模误差,提高建模精度。
1建立焊接环境模型
焊缝模型是指焊缝坐标系与世界坐标系的变换矩阵。因此只需要对世界坐标系、测量坐标系、焊件坐标系和焊缝坐标系之间的关系进行研究。各坐标系采用D-H方法建立,如图1所示。

图1 焊接系统坐标系模型
图中坐标系W为世界坐标系;坐标系M为测量坐标系;坐标系C为工件坐标系;坐标系P为焊缝坐标系。其中测量坐标系M的ZM坐标轴与世界坐标系w的ZW轴平行且指向同一个方向。点A和点B是世界坐标系中的两个相异的辅助特征点。系统的工作流程叙述如下:①通过测量设备,测量辅助特征点A和点B在测量坐标系中的坐标值;②根据辅助两点坐标系标定算法计算测量坐标系相对世界坐标系的变换矩阵[12];③通过测量设备,测量工件特征点在测量坐标系中的坐标值,建立焊缝位置模型;④根据等分离散算法建立焊缝特征模型;⑤根据焊接工艺要求建立焊枪位姿模型;⑥根据焊枪位姿模型控制机器人运动实现焊接。
2建立管道插接相贯线焊缝数学模型

工件上的特征点Pi(i=1、2…6)在测量坐标系中的坐标为(xi,yi,zi),根据几何知识可知,根据点P1、P2、P3可以计算主管的中心线向量V1,根据点,P4、P5、P6可以计算支管中心线向量V2:
(1)
式中,符号‘^’是向量积运算符。
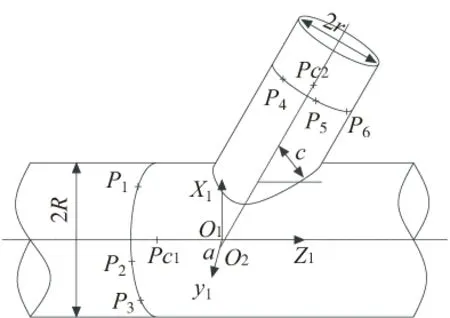
图2 管道插接模型
根据中垂线垂直于弦和平面法向量,可以计算出中垂线的方向向量:
(2)
弦的中点坐标值:
(3)
中垂线通过弦的中点,可以建立中垂线的参数方程:
(4)
式中Pc1是主管圆心坐标,P21是支管圆心坐标,t11、t12、t21、t22是中垂线方程的参数。圆的半径可由下式计算:
(5)
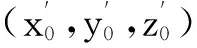
(6)
整理式(6)得关于参数t1和t2的方程:
(7)
计算出t1和 t2的值后,带入主管和支管中心线方程,既可以求得点O1和点O2的坐标值。则可得坐标系X1Y1O1Z1在测量坐标系中的平移矩阵:
P=[x0;y0;z0]
(8)
偏心距a可根据两点间的距离公式计算,即向量O1O2的模:
a=‖O1O2‖
(9)
相贯角c即为两圆管中心线的夹角(取小于90°的角):
(10)
坐标系X1Y1O1Z1的Y轴与O1O2重合,Z轴与主管中心线重合,X轴由右手定则确定。因此坐标系X1Y1O1Z1在测量坐标系中的旋转矩阵为:
RMC=[O1O2^V1;O1O2;V1]T
(11)
文献[8]中给出了相贯线在坐标系X1Y1O1Z1中的参数方程:
(12)
相贯线离散化处理后得到一组离散点Pi(i=0、1…n),根据坐标转换理论,相贯线的离散点在世界坐标系中的表达式为:
(13)
3焊缝特征模型
相贯线特征模型如图3所示,相贯线上任意点的切线,始终与过该点的两个圆柱切平面的交线重合[8]。设过相贯线上P点且与主管相切的平面A的法线矢量为S1(X1,Y1,Z1), 与支管相切的平面B的法线矢量为S2(X2,Y2,Z2)。
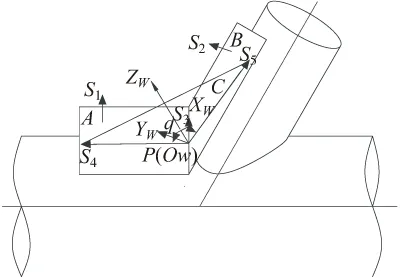
图3 相贯线焊缝坐标系示意图
文献[8]中给出了法线矢量S1和S2的表达式:
(14)
(15)
设平面A和平面B的交线的矢量为S3(X3,Y3,Z3),根据两平面相交线求法可得:
S3=S1^S2
(16)
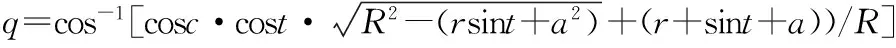
(17)
定义焊缝坐标系XwYwOwZw:原点Ow位于焊缝当前焊接点(上述的P点),Xw轴为相贯线上该点的切线且方向指向焊接方向,Zw轴为相贯线主管切平面与支管切片面的角平分线,方向由焊缝指向外面,Yw轴方向可以根据右手定则来确定。Zw轴可认为是矢量S4绕Xw旋转q/2角得到的。则旋转矩阵表达式:
S4=S1^S3
Rc=[ S3;S4^S3;S4]T·R(Xw,q/2)
(18)
相贯线是连续封闭的曲线,需要进行分段处理后才能采用等分离散算法进行建模。按照等弧长离散原理将曲线离散为弧长相等的曲线,分别建立各段弧长起点和终点的旋转矩阵。空间两点间的坐标系变换原理如图4所示。

图4 坐标系变换原理图
图中,空间中任意一条曲线AB,起点A的坐标系在世界坐标系中的旋转矩阵为RA,终点B的坐标系在世界坐标系中的旋转矩阵为RB,坐标系B在坐标系A中的旋转矩阵为RAB:
RAB=RARB
(19)

(20)
(21)
根据Euler定理可得:

(22)
(23)
(24)
(25)
曲线AB采用等弧长离散方法离散为n个点,则旋转角度φ等分为n-1份,即,φi[0,φ],i=0、1、2…,n。将φi的值带入式24和式25,即可解得各离散点处的旋转矩阵。
4Matlab仿真分析
在matlab环境下,用工具guide创建了图形仿真界面。通过界面可从图形窗口输出对应的仿真结果。
图5中显示的相贯线是两个圆柱面的交线。图中“黑色箭头线”是采用直接在离散点处建立焊缝特征模型的Z轴,“红色箭头线”是采用文中的等分离散算法建立的焊缝特征模型的Z轴,两组箭头线方向几乎一致,表明所建立的焊缝特征模型是正确的。

图5 相贯线焊缝特征模型
图6是采用两种建模方法建立的特征模型的Z轴的夹角曲线图。该图是将曲线先分成16段,再采用的等分离散算法分别对每一段曲线建立焊缝特征模型,从图中可以看出,夹角最大值为2.074°,在焊接允许范围内。因此,采用等分离散算法可以建立理想的管道插接焊缝模型。

图6 特征模型误差曲线
5结论
文中采用测量工件上6个特征点的方法,建立了管道插接相贯线的数学模型。提出了采用旋量理论的等分离散方法建模焊缝特征模型的方法。在matlab环境下,对采用直接建模方法和采用等分离散算法建立的管道插接焊缝特征模型的的误差进行了对比分析,仿真结果表明:采用等分离散算法可以建立理想的螺旋线和相贯线的焊缝特征模型,且建模方法简单,效率高。
[参考文献]
[1]JoubairA,BonevIA.Non-kinematiccalibrationofasix-axisserialrobotusingplanarconstraints[J].PrecisionEngineering, 2015, 40:325-333.
[2] 诸葛琰,卓雪艳,廖小平,等.OTC弧焊机器人离线编程系统开发[J].组合机床与自动化加工技术,2015,11,91-94.[3]ShiH,SuHJ,DagalakisN,etal.Kinematicmodelingandcalibrationofaflexurebasedhexapodnanopositioner[J].PrecisEng, 2013, 37(1):117-28.
[4] 高文斌, 王洪光, 姜勇, 等. 基于距离误差的机器人运动学参数标定方法[J]. 机器人,2013, 35(5):600-606.
[5]ChenXZ,HuangYM,ChenSB.Modelanalysisandexperimentaltechniqueoncomputingaccuracyofseamspatialpositioninformationbasedonstereovisionforweldingrobot.IndustrialRobotanInternationalJournal, 2012,39(4):349-356.[6]YiYM,LiuD.SimultaneousLocalizationandMappingUsingMonocularVision.JournalOfNanoelectronicsAndOptoelectronics, 2012, 7(2):162-166.
[7]KimMY,LeeH,ChoH.Denserangemapreconstructionfromaversatileroboticsensorsystemwithanactivetrinocularvisionandapassivebinocularvision[J].AppliedOptics2008, 47(11):1927-1939.
[8] 任福深,陈树君,殷树言,等.管道插接焊缝位置及焊枪位姿建模[J].焊接学报,2008,29(11):33-36.
[9]ShiL,TianXC.Automationofmainpipe-rotatingweldingschemeforintersectingpipes[J].IntJAdvManufTechnol, 2015, 77:955-964.
[10]LuY,TianXC,LiangJ.Trackcontrolinautomatedweldingofsaddlecurve[J].JSciIndRes,2010,69(11):811-817.
[11]MehrdadBS,MaryamA,MoosavianS.AliA.Designandanalysisofaweldingrobot[C].IEEEInternationalConferenceAutomationScienceandEngineering.Newyork,NY,USA:IEEE, 2006:454-459.
[12] 赵艳丽,肖金陵.激光加工机械手系统工件位姿自动校正的方法[J].激光技术, 2015, 39(2):206-208.
(编辑赵蓉)
Establishing Method of Mathematical Models for Complex Weld Based on Reverse Modeling
LI Jing1,LI Jun2,HAO Wei-dong2
(1.School of Mechanical and Electrical Engineering,Institute of Information Technology of Guet,Guilin Guangxi 541004,China;2.School of Mechanical and Electrical Engineering, Guilin University of Electronic Technology, Guilin Guangxi 541004,China)
Abstract:The method of mathematical model establishment is more complicated in the automatic welding of complex welding seam at present. An algorithm for discrete aliquot is proposed in this paper for complex weld. It measures points on the work piece using independent measuring device. The rotation matrix between coordinate system for two points on the curve is known, the rotation matrix converted to exponential mapping by Euler, coordinate other point is to be established by an method of the rotation angle for the aliquot. Intersecting pipes is established and analysis in Matlab. The results show that the algorithm using discrete aliquot weld build feature model can achieve expectation effect. This method makes the operation simpler, more efficient.
Key words:model of complex weld; reverse modeling; discrete algorithms; intersecting pipes
文章编号:1001-2265(2016)06-0043-04
DOI:10.13462/j.cnki.mmtamt.2016.06.011
收稿日期:2015-12-15;修回日期:2016-01-20
*基金项目:国家自然科学基金项目(51506033)
作者简介:李静(1983—),女,陕西澄城县人,桂林电子科技大学信息科技学院讲师,工学硕士,研究方向为机器人技术、机械电子技术应用,(E-mail)jinglijl@126.com。
中图分类号:TTH166;TG506
文献标识码:A

