预紧力作用下滚珠丝杠温升的理论分析及试验研究*

王　立，周长光,祖　莉，冯虎田

(南京理工大学 机械工程学院，南京　221000)

预紧力作用下滚珠丝杠温升的理论分析及试验研究*

王立，周长光,祖莉，冯虎田

(南京理工大学 机械工程学院，南京221000)

摘要：滚珠丝杠的温升直接影响其使用的精度，通过误差补偿技术可以解决这一问题，为了研究预紧力作用下丝杠的温升情况，通过摩擦生热和热对流原理建立了计算滚珠丝杠副温升的理论模型，探究了丝杠温升与预紧力的关系。将通过该模型计算的不同预紧力下的理论温升，与试验测得的试验温升进行对比分析，试验结果证实了该计算模型的正确性。该模型对于滚珠丝杠在使用中的热变形误差补偿具有十分重要的意义。

关键词：预紧力；摩擦力矩；热对流；温升

0前言

精密滚珠丝杠副是数控机床的关键功能部件[1]，为了提高滚珠丝杠的使用精度，通常采用预紧技术对间隙进行消除，但是预紧力会增大滚珠丝杠的温升。目前国内对于滚珠丝杠温升的研究多数为温度场热特性仿真[3]，于旭年等人提出丝杠温升与摩擦力矩几乎成比例关系，并分析了温升的主要来源[4]；在计算螺母发热量时，国内外学者几乎全部采用统一的摩擦公式[8]，但此公式的正确性尚不得而知。为了准确的探讨丝杠温升与预紧力的具体公式，本文通过摩擦生热及热对流原理，建立了丝杠温升的计算模型，通过试验验证了理论分析的正确性。

1理论分析

1.1滚珠丝杠的温升与发热量

滚珠丝杠运行过程中的温升主要来自于滚珠与滚道之间的摩擦以及轴承的生热。由于丝杠与螺母并不直接接触，可以认为滚珠与丝杠滚道单位时间内摩擦产生热量Q1全部被滚珠与丝杠吸收，由于滚珠的质量与螺母相比很小，可以假定热量全部转化为丝杠的温升。丝杠两端的轴承单位时间内产生的热量Q2一半被头尾架吸收，一半被丝杠吸收。在丝杠升温的过程中，由于丝杠与环境的温差，有一部分热量Q3以热对流的形式传递到空气中。当在某一单位时间内丝杠吸收的热量与热对流的散失热量相等，即：

(1)

滚珠丝杠副的温度达到稳定状态，此时丝杠温度不再增加，保持恒定。

利用轴承发热计算公式[8]，可以求得轴承单位时间的发热量：

Q2=1.047×10-4nM

(2)

其中，n—转速，r/min；

M—轴承的摩擦力矩，N·mm。

丝杠运行过程中某一单位时间内与空气通过热对流散失的热量：

Q3=h·A·ΔT=h·A·(TS-Ta)

(3)

其中，h—空气的热对流系数：

h=λNm/d

(4)

其中， λ—空气导热系数；

Nm—努谢尔特数：

(5)

其中，Re—雷诺系数：

Re=ωd2/ν

(6)

ν—空气的运动粘度。

ΔT—某一时刻丝杠与空气的温差，达到热平衡时也就是丝杠稳定后的温升值。

Ts—某一时刻丝杠的温度；

Ta—某一时刻的空气温度，由于试验在恒温室中进行，故Ta≡21℃。

1.2丝杠摩擦生热计算

丝杠运行过程中几乎全部的热量都来自于滚珠与滚道之间的摩擦生热，根据摩擦生热的公式：

Q=F×S

(7)

Q—发热总量；

F—滚珠滚道之间摩擦力：

F=μP

(8)

其中，μ—滑动摩擦系数。

S—相对行程。

在丝杠运行过程中，滚珠体不仅存在滚动，还时刻存在着滑动，这也是摩擦产生的主要原因，由于滚动摩擦产生的热量很小，我们可以认为丝杠运行时的发热量全部来自于滑动摩擦。滚珠与丝杠的相对滑动行程

(9)

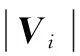
(10)

wm—滚珠相对于丝杠公转角速度：

(11)

wR—滚珠自转角速度：

(12)

wt=wRcosβsinβ′

(13)

wb=-wRcosβcosβ′

(14)

wn=-wRsinβ

(15)

其中，

(16)

β通常取45°，β′通常取0。

通过公式(2)、(3)和(7)分别求出滚珠丝杠吸收的与散失的热量，代入公式(1)即可求出达到热稳定时丝杠的温升ΔT。

1.3接触面受力分析

图1为仅受轴向预紧力时的滚珠螺旋副受力情况。

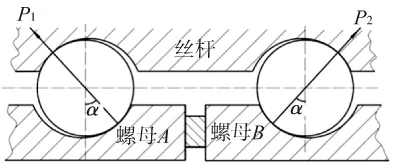
图1　预紧力作用下滚珠受力情况

仅承受轴向预紧力的双螺母垫片预紧滚珠丝杠副，在滚珠与滚道接触面处产生法向压力P，单个螺母内所有工作滚珠承受的法向力的轴向分量之和应该与预紧力相等，即：

FP=zPa

(17)

z—单个螺母中工作滚珠个数[6]：

(18)

θ—相邻滚珠之间的相位角：

(19)

其中，rb—滚珠半径；

rm—丝杠半径；

i—单个螺母中工作的滚珠圈数×列数；

γ—螺旋升角；

取单个滚珠作受力分析，如图2所示。

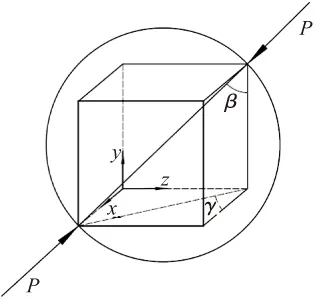
图2　滚珠受力分析图

(20)

故

FP=zPsinαcosγ

(21)

其中，α—接触角。

1.4预紧力与摩擦力矩

根据kragelsky等人的分析[9]，单个滚与螺母、丝杆滚道之间的总摩擦力矩：

Mf=M0+Mg+Mh

(22)

M0—初始变形(主要由预紧力决定)带来的摩擦力矩；Mg—制造加工误差带来的摩擦力矩；Mh—滚珠冲击力带来的摩擦力矩。

由以上分析可知，若忽略滚道加工误差带来的影响，在滚珠丝杠低速运转时，由于滚珠与反向器的冲击非常小，不受轴向载荷的滚珠丝杠摩擦力矩可以近似看作全部来自于轴向预紧力带来的相对变形。这也是实际应用中可以用摩擦力矩测量近似描述预紧力大小的依据。

根据目前国内知名厂家认可并采用的动态预紧转矩测量规范[10]，滚珠丝杠副的动态预紧转矩：

(23)

FPr— 轴向预加载荷(N)；

Ph— 导程(mm)；

η—传动效率：

一般，精度1、2级，取η=0.95；3、4级取η=0.9；5、7、10级取η=0.85(具体查阅厂家技术手册)

由上式可知，假定在滚珠丝杠运行过程中效率η为一定值，则动态预紧转矩TP0和轴向预紧力FPr呈线性关系。由于滚珠丝杠摩擦力矩主要是由动态预紧转矩和垫片的摩擦力矩等组成，而垫片的摩擦力矩又近似为常数，因此可认为摩擦力矩与预紧力也呈线性关系。故可以通过测量丝杠使用不同时间之后的摩擦力矩间接得到预紧力的大小，进而研究预紧力与丝杠发热量的关系。

2试验条件

2.1试验台简介

高速滚珠丝杠副综合性能试验台是针对高速滚珠丝杠的综合性能的测量设计开发的一台高可靠性高应用性的试验台，主要用于测量丝杠的精度(定位精度和行程误差)及综合性能(噪声、温升、摩擦力矩、热伸长、输入力矩和加速度)。

试验台测试对象主要是中径φ63mm及以下的滚珠丝杠副，总长不超过2m；试验台长3.2m，宽1.14m，高0.8m。实物图如图3所示。

图3　综合性能试验台

试验台数据采集模块与驱动控制模块分开控制。数据采集模块通过工业控制PCI1713板卡进行；选用西门子伺服电机1FT6084进行直连驱动，电机额定功率10.68kW，额定转速6000r/min，满足高速要求；同时与之配套的西门子828D数控系统控制伺服电机驱动测量平台往返运动。

2.2滚珠丝杠副温升测量

选用北京昆仑海岸传感器技术中心的温度传感器，该传感器的热敏感元件为Pt100，测量范围是-20℃～100℃。Pt100输出信号为阻抗信号，需要外加电路将其变换成电信号传递给工控机，因此将传感器输出端接入温度变送器。温度变送器选用昆仑海岸传感器技术中心的TT4C-V，该款温度变送器通过RS232 接口将测得数据传入工控机，通过24V直流稳压电源供电。

将贴片式温度传感器直接贴在滚珠丝杠副的丝杠上，采集到的信号经过温度变送器传入工控机，经过软件处理后变位温度信号并显示在计算机上，形成温度变化曲线。

2.3滚珠丝杠摩擦力矩测量

进行滚珠丝杠副摩擦力矩测量试验时，在与工作台相连接的V型块上通过螺钉连接推动装置，丝杠转动时，推动装置给予试验台运动的推/拉力，将螺母从工作台中脱出；利用螺母上的油孔连接一个传力臂，传力臂由静态扭矩传感器固定，限制螺母的自由转动，同时将摩擦力矩传递到力矩传感器，传力图如图4所示。

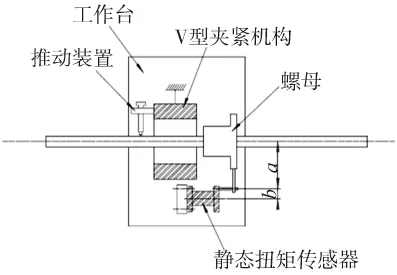
图4　摩擦力矩测量示意图

假设在传力杆与受力杆接触点处的作用力为F，则静态扭矩传感器测得的扭矩Tc=F·b，由作用力与反作用力的原理可知，螺母与丝杠的实际摩擦力矩Ts=F·a，因此可知实际摩擦力矩与测得的扭矩之间的关系：

(24)

2.4轴承摩擦力矩测量

试验台使用美国FUTEK公司的TRS600扭矩传感器测量输入扭矩，传感器连接在丝杠轴与电机轴之间，可以十分准确的测量出电机输出的扭矩值。在试验中，将关乎丝杠螺母与工作台脱离开来，使电机带动丝杠做空转运动，此时电机输出的扭矩就是两支撑端轴承的摩擦力矩。

3试验

3.1样件

试验产品为国内某厂家生产的双螺母垫片预紧滚珠丝杠副。其各项参数如表1所示。

表1　试验丝杠参数表

3.2实验过程：

(1)丝杠以1000r/min转速运行1000万转，初始、每隔100万转、结束测量一次摩擦力矩，输出报表。

(2)每一次测量摩擦力矩后以2000r/min高速运行至螺母温升曲线达到平稳，记录下螺母和丝杠的温升值。

(3)为保证良好均等的润滑条件，每隔100万转加等量润滑脂。

3.3实验结果

图5为100万转过后所测得的120min内螺母温升的原始曲线。

从图中可以看出，经过大约100min后螺母温升接近直线，温度近乎不再变化。为了保证试验的准确性，我们取120min的温升作为最终试验结果进行后续分析。

图5　120min螺母温升曲线

表2与表3分别为各阶段摩擦力矩测量结果以及通过公式(23)计算出的对应预紧力大小。表4为每次测得的120min后丝杠温度相对于环境温度的增值。

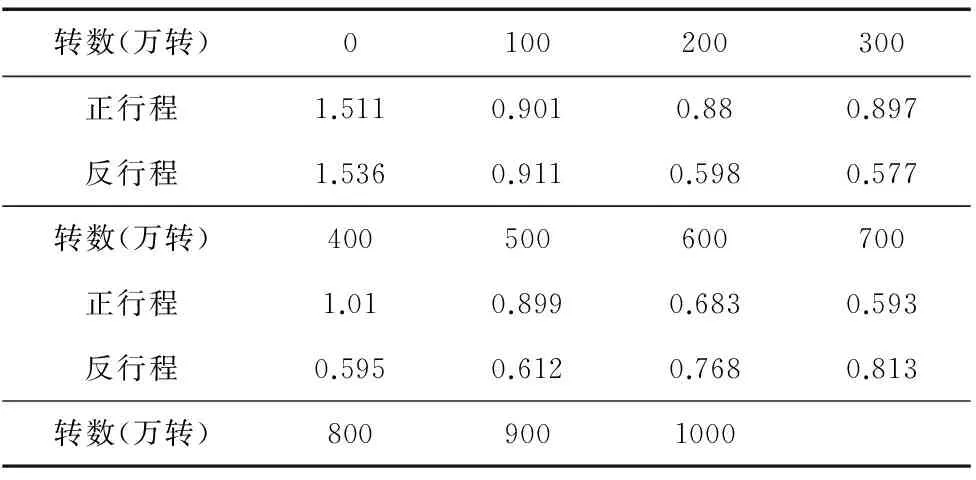
表2　每隔100万转所测的摩擦力矩(Nm)

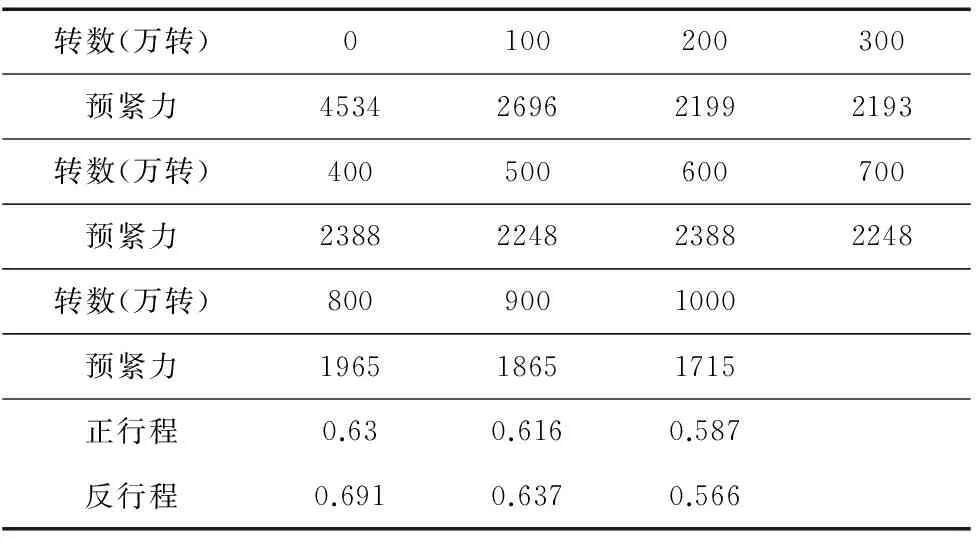
表3　每隔100万转所计算的预紧力(N)

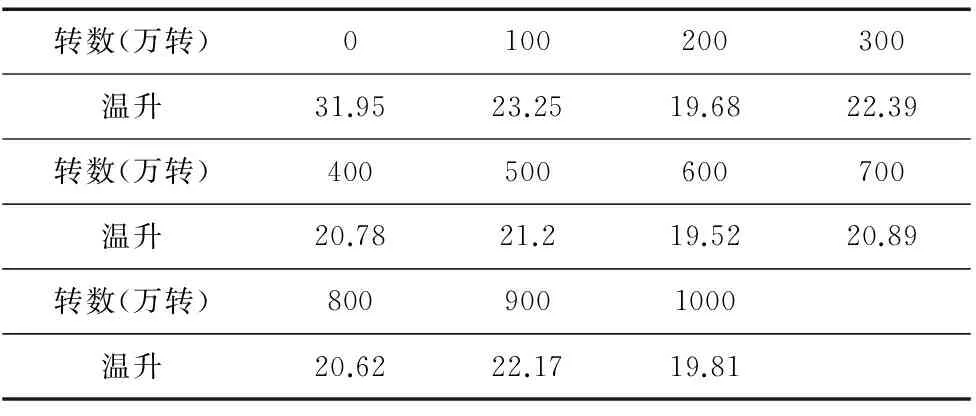
表4　每隔阶段120min丝杠的温升实验数据

4试验结果分析

4.1试验与理论结果对比

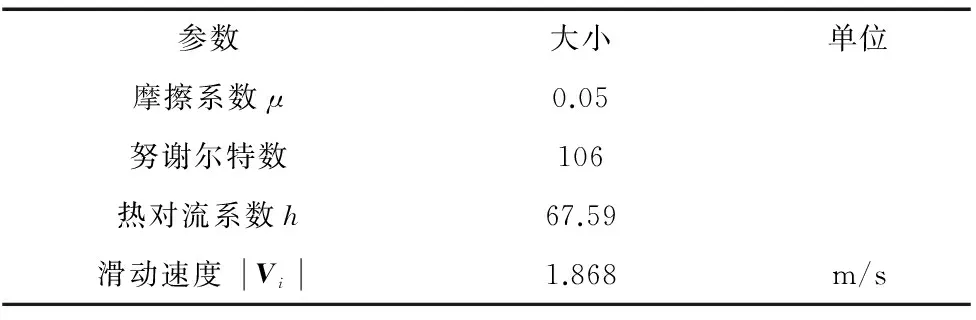
计算发热量所需要的一些计算参数如表5所示。

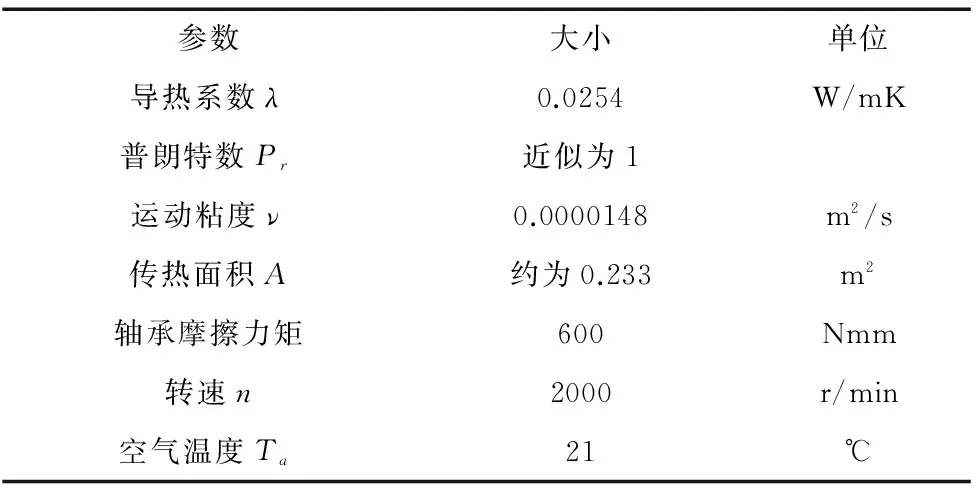
表5　理论计算参数表

续表

通过前面公式中的理论模型计算，得到丝杠达到稳定状态时相对于空气温度对应各个转数阶段的变化量如表6所示。

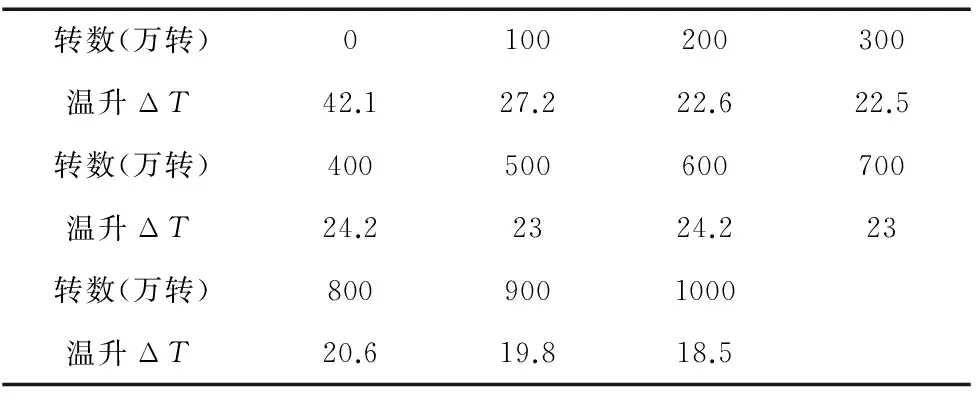
表6　丝杠温升计算结果

图6为测得的预紧力随着运转圈数的变化曲线；图7为理论计算的丝杠温升与试验测得丝杠温升的对比曲线。

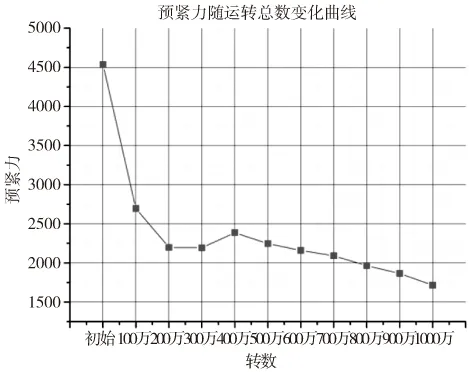
图6　预紧力丧失曲线

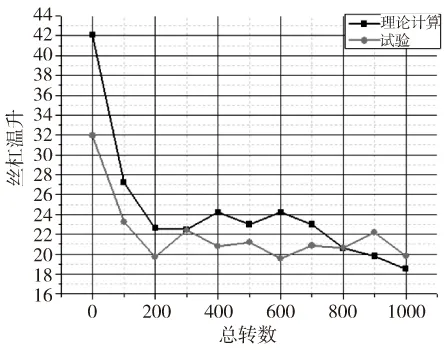
图7　理论与试验温升结果对比图

4.2结果分析

通过预紧力的变化曲线以及温升理论与实验结果的对比，可以分析出如下结果：

(1)从单次测量的丝杠温升曲线来看，温升的速度随着时间逐步减缓，最终会达到平稳状态，而平稳时的值对于我们进行误差补偿十分重要。

(2)预紧力在初始的200万转丧失的速度很快，后面进入平稳伴随小幅下降的趋势。试验测得的温升曲线与预紧力丧失趋势十分吻合，证明在无外部载荷的情况下温升值与预紧力大小息息相关。

(3)在最开始的200万转，当预紧力较大时，温升的理论结果与试验结果相差较大，主要原因是在120min的测量过程中，预紧力会出现快速下降，这一点从预紧力测量曲线可以看出，而我们在计算中则以试验开始时的预紧力作为计算参数，并未考虑测量过程中的预紧力丧失，故计算结果比实验结果大。

5结论

通过实验结果与理论计算结果的对比可知，滚珠丝杠温升的试验结果与通过理论模型计算的结果具有高度一致性，这一结论充分证明了理论计算模型的正确性。同时，试验结果也向我们充分展示了滚珠丝杠在使用过程中预紧力的丧失情况。

丝杠温升和预紧力丧失都是影响丝杠使用精度的重要因素，也是目前很多生产企业十分关注并且急需解决的问题。上述理论模型为滚珠丝杠使用中建立误差补偿具有十分重要的意义。

[参考文献]

[1] 韩新建. 高速滚珠丝杠副摩擦性能分析及实验研究[D]. 兰州:兰州理工大学,2011.

[2] 初永坤, 李益民, 白绥滨. 精密滚珠丝杠副螺母预紧的方法[J]. 机械工艺师，1996(9):15-16.

[3] 周云龙, 王义. 关于机床滚动轴承和滚珠丝杠的预紧方法的分析[J]. 硅谷，2013(4)：111-113.

[4] 于旭年, 荆福义. 滚珠丝杠的温升及热变形对策[J]. 农业装备与车辆工程，2005(3)：40-44.

[5] 杨锦斌, 杨维平, 黄桂英，等. 滚珠丝杠副热位移的抑制对策[J]. 制造技术与机床，2006(8)：109-111.

[6] 江洪奎.大导程滚珠丝杠副动力学性能及加工方法研究[D]. 济南:山东大学,2007.

[7] M C Lin, B Ravani, S A Velinsky. Kinematics of the Ball Screw Mechanism[J]. Journal of Mechanical Design，1996，116：849-855.

[8] Z Z Xu, X J Liu, H K Kim, et al. Thermal error forcast and performance evaluation for an air-cooling ball screw system[J]. International Journal of Machine Tools & Manufacture，2011，51：605-611.

[9] 黄寿荣, 黄家贤. 滚珠丝杠摩擦力矩影响因素的分析[J]. 东南大学学报，1993，23(S)：125-138.

[10] 程光仁.滚珠螺旋传动设计基础[M]. 北京：北京机械工业出版社，1987.

(编辑赵蓉)

Theoretical Analysis and Experimental Study of Temperature Rise for Pre-tightening Ball Screw

WANG Li，ZHOU Chang-guang，ZU Li，FENG Hu-tian

(School of Mechanical Engineering,Nanjing University of Science and Technology, Nanjing 221000,China)

Abstract：The temperature rise of the ball screw directly affects the accuracy. Error compensation can solve this problem effectively. In order to study the temperature rise of ball screw under the pre-tightening force, a theoretical calculation of ball screw temperature rise was established based on the principle of friction heat and heat convection. The temperature rises under different pre-tightening forces were calculated, and the results were compared with the experimental results. Through these works, the calculation was proved to be correct and is very important for the error compensation of ball screw.

Key words：pre-tightening force; friction torque; heat convection; temperature rise

文章编号：1001-2265(2016)06-0001-04

DOI:10.13462/j.cnki.mmtamt.2016.06.001

收稿日期：2015-08-06；修回日期：2015-08-29

*基金项目：国家科技重大专项(2012ZX04002021)

作者简介：王立(1990—)，男，江苏徐州人，南京理工大学硕士研究生，研究方向为滚动功能部件共性技术和精密机电测控技术，(E-mail)772966503@qq.com；通讯作者：祖莉(1977—)，女，南京人，南京理工大学副教授，博士，研究方向为精密传动、智能系统机构学与动力学研究，(E-mail)mzmllovey@vip.sina.com。

中图分类号：TH162;TG506

文献标识码：A